Which of the following are the roots of

The given equation is $\left(3 \mathrm{x}^{2}+2 \mathrm{x}-1=0\right)$.

(i) $\mathrm{x}=(-1)$

L.H .S. $=\mathrm{x}^{2}+2 \mathrm{x}-1$

$=3 \times(-1)^{2}+2 \times(-1)-1$

$=3-2-1$

$=0$

$=$ R.H.S.

Thus, $(-1)$ is a root of $\left(3 x^{2}+2 x-1=0\right)$.

(ii) On substituting $\mathrm{x}=\frac{1}{3}$ in the given equation, we get:

L.H.S. $=3 \mathrm{x}^{2}+2 \mathrm{x}-1$

$=3 \times\left(\frac{1}{3}\right)^{2}+2 \times \frac{1}{3}-1$

$=\not{3}^{1} \times \frac{1}{-9_{3}}+\frac{2}{3}-1$

$=\frac{1+2-3}{3}$

$=\frac{0}{3}$

$=0$

$=$ R.H.S.

Thus, $\left(\frac{1}{3}\right)$ is a root of $\left(3 \mathrm{x}^{2}+2 \mathrm{x}-1=0\right)$.

(iii) On substituting $\mathrm{x}=\left(-\frac{1}{2}\right)$ in the given equation, we get:

L.H.S. $=3 x^{2}+2 x-1$

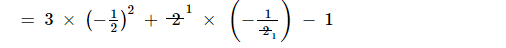
$=3 \times \frac{1}{4}-1-1$

$=\frac{3}{4}-2$

$=\frac{3-8}{4}$

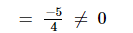
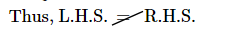
Hence, $\left(-\frac{1}{2}\right)$ is a not solution of $\left(3 \mathrm{x}^{2}+2 \mathrm{x}-1=0\right)$