Which of the following is a false statement?
(a) A median of a triangle divides it into two triangles of equal areas.
(b) The diagonals of a || gm divide it into four triangles of equal areas.
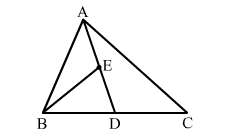
(c) In a $\triangle A B C$, if $E$ is the midpoint of median $A D$, then $\operatorname{ar}(\Delta B E D)=\frac{1}{4} \operatorname{ar}(\Delta A B C)$.
(d) In a trap. ABCD, it is given that AB || DC and the diagonals AC and BD intersect at O. Then, ar(∆AOB) = ar(∆COD).
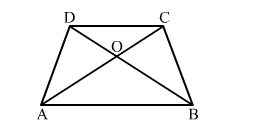
(d) In a trap. ABCD, it is given that AB || DC and the diagonals AC and BD intersect at O. Then ar(∆AOB) = ar(∆COD).
Consider ∆ADB and ∆ADC, which do not lie on the same base but lie between same parallel lines.
i.e., ar(∆ADB)
Subtracting $\operatorname{ar}(\triangle A O D)$ from both sides, we get:
$\operatorname{ar}(\triangle A D B)-\operatorname{ar}(\triangle A O D) \neq \operatorname{ar}(\triangle A D C)-\operatorname{ar}(\triangle A O D)$
$\operatorname{Or} \operatorname{ar}(\Delta A O B) \neq \operatorname{ar}(\Delta C O D)$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.