Which of the following points lies on the locus of the foot of perpendicular drawn upon any

Let foot of perpendicular is $(\mathrm{h}, \mathrm{k})$

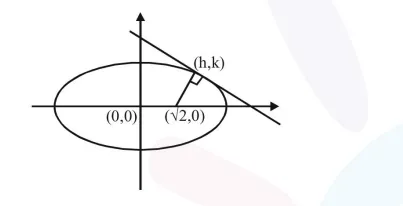
$\frac{x^{2}}{4}+\frac{y^{2}}{2}=1$ (Given)

$a=2, b=\sqrt{2}, e=\sqrt{1-\frac{2}{4}}=\frac{1}{\sqrt{2}}$

$\therefore$ Focus $(\mathrm{ae}, 0)=(\sqrt{2}, 0)$

Equation of tangent

$y=m x+\sqrt{a^{2} m^{2}+b^{2}}$

$y=m x+\sqrt{4 m^{2}+2}$

Passes throguh $(h, k)$

$(\mathrm{k}-\mathrm{mh})^{2}=4 \mathrm{~m}^{2}+2$ .................(1)

line perpendicular to tangent will have slope

$-\frac{1}{m}$

$y-0=-\frac{1}{m}(x-\sqrt{2})$

$m y=-x+\sqrt{2}$

$(h+m k)^{2}=2$ .............(2)

Add equaiton (1) and (2)

$\mathrm{k}^{2}\left(1+\mathrm{m}^{2}\right)+\mathrm{h}^{2}\left(1+\mathrm{m}^{2}\right)=4\left(1+\mathrm{m}^{2}\right)$

$\mathrm{h}^{2}+\mathrm{k}^{2}=4$

$\mathrm{x}^{2}+\mathrm{y}^{2}=4$ (Auxilary circle)

$\therefore(-1, \sqrt{3})$ lies on the locus.