Write the formula for the area of a segment

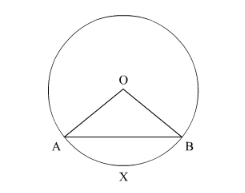
In this figure, centre of the circle is $O$, radius $O A=r$ and $\angle A O B=\theta$

We are going to find the area of the segment AXB.

Area of the segment $A X B=$ Area of the sector $O A X B$ - Area of $\triangle A O B$

We know that area of the sector $O A X B=\frac{\theta}{360} \times \pi r^{2}$

We also know that area of $\triangle A O B=r^{2} \sin \frac{\theta}{2} \cos \frac{\theta}{2}$

Substituting these values in equation (1) we get,

Area of the segment $A X B=\frac{\theta}{360} \times \pi r^{2}-r^{2} \sin \frac{\theta}{2} \cos \frac{\theta}{2}$

Area of the segment $A X B=\left(\frac{\theta}{360} \times \pi-\sin \frac{\theta}{2} \cos \frac{\theta}{2}\right) r^{2}$

So, Area of the segment $A X B=\left(\frac{\pi \theta}{360}-\sin \frac{\theta}{2} \cos \frac{\theta}{2}\right) r^{2}$

Therefore, area of the segment is $\left(\frac{\pi \theta}{360}-\sin \frac{\theta}{2} \cos \frac{\theta}{2}\right) r^{2}$.