Start Prep From 0 & Get IIT Bombay with Most Powerful JEE Dropper Course
Enroll Now!

Quadratic Equation - JEE Advanced Previous Year Questions with Solutions

JEE Advanced Quadratic Equations PYQs cover root conditions, complex numbers, recurrence relations, common roots, inequalities, trigonometric roots, and sequence-based applications, helping students master advanced algebraic concepts and exam-level problem-solving techniques.

eSaral Updated on:
Quadratic Equation - JEE Advanced Previous Year Questions with Solutions

› JEE › JEE Main ›Quadratic Equation - JEE Advanced Previous Year Questions with Solutions

esaral jee batches

🚀 Checkout eSaral Courses

JEE Advanced Previous Year Questions of Math with Solutions are available at eSaral. Practicing JEE Advanced Previous Year Papers Questions of mathematics will help the JEE aspirants in realizing the question pattern as well as help in analyzing weak & strong areas. eSaral helps the students in clearing and understanding each topic in a better way. eSaral also provides complete chapter-wise notes of Class 11th and 12th both for all subjects. Besides this, eSaral also offers NCERT Solutions, Previous year questions for JEE Main and Advance, Practice questions, Test Series for JEE Main, JEE Advanced and NEET, Important questions of Physics, Chemistry, Math, and Biology and many more. Download eSaral app for free study material and video tutorials.     Simulator   Previous Years JEE Advanced Questions

Q. The smallest value of $\mathrm{k},$ for which both the roots of the equation, $\mathrm{x}^{2}-8 \mathrm{kx}+16\left(\mathrm{k}^{2}-\mathrm{k}+1\right)=0$ are real, distinct and have values at least $4,$ is [JEE 2009, 4 (–1)]
Ans. 2
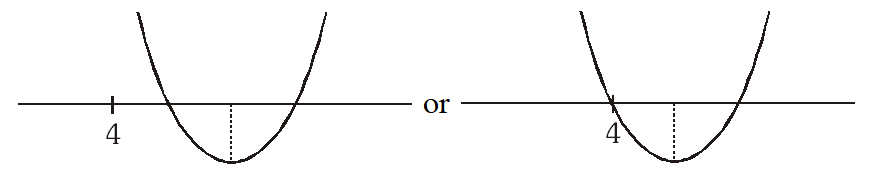
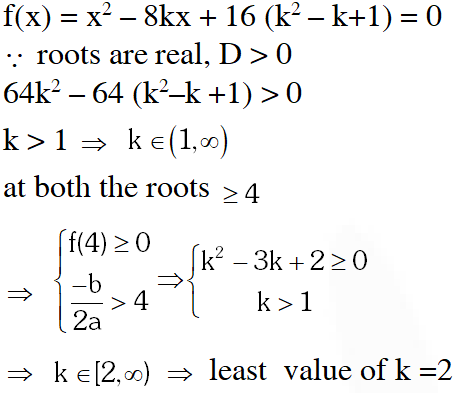
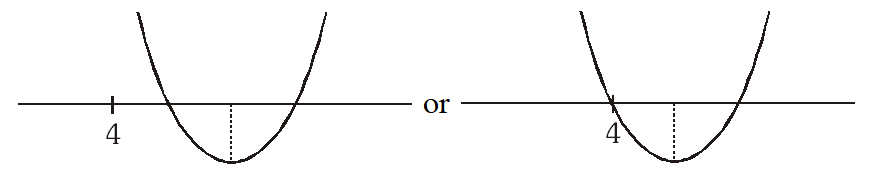
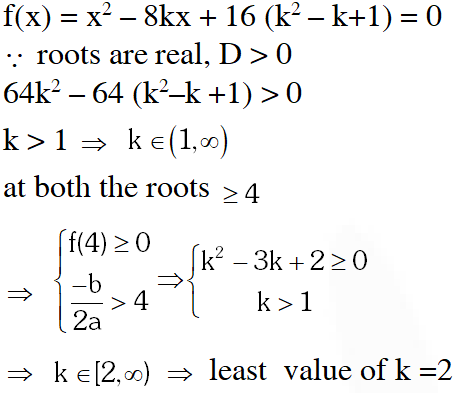
Q. Let p and q be real numbers such that $p \neq 0, p^{3} \neq q$ and $p^{3} \neq-q .$ If $\alpha$ and $\beta$ are nonzero complex numbers satisfying $\alpha+\beta=-p$ and $\alpha^{3}+\beta^{3}=q$, then a quadratic equation having $\frac{\alpha}{\beta}$ and $\frac{\beta}{\alpha}$ as its roots is (A) $\left(p^{3}+q\right) x^{2}-\left(p^{3}+2 q\right) x+\left(p^{3}+q\right)=0$ (B) $\left(\mathrm{p}^{3}+\mathrm{q}\right) \mathrm{x}^{2}-\left(\mathrm{p}^{3}-2 \mathrm{q}\right) \mathrm{x}+\left(\mathrm{p}^{3}+\mathrm{q}\right)=0$ (C) $\left(\mathrm{p}^{3}-\mathrm{q}\right) \mathrm{x}^{2}-\left(5 \mathrm{p}^{3}-2 \mathrm{q}\right) \mathrm{x}+\left(\mathrm{p}^{3}-\mathrm{q}\right)=0$ (D) $\left(p^{3}-q\right) x^{2}-\left(5 p^{3}+2 q\right) x+\left(p^{3}-q\right)=0$ [JEE 2010, 3]
Ans. (B)
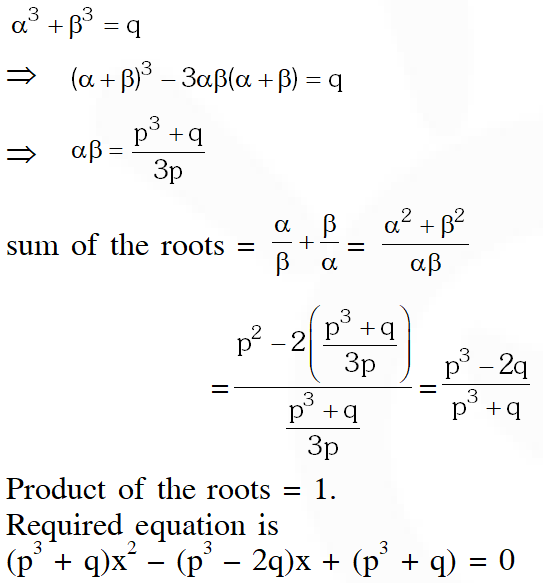
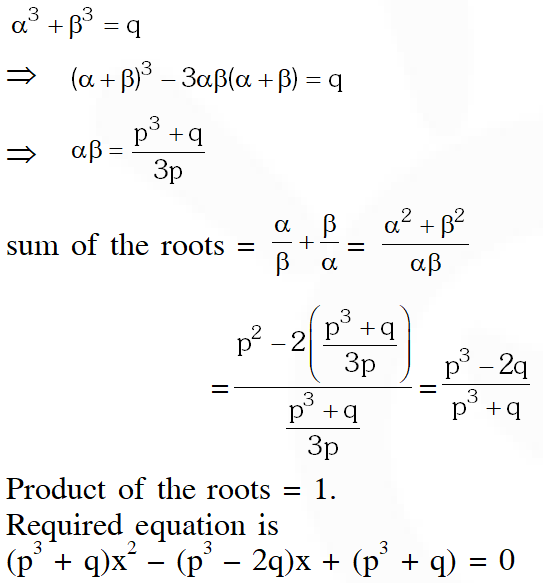
Q. Let $\alpha$ and $\beta$ be the roots of $\mathrm{x}^{2}-6 \mathrm{x}-2=0,$ with $\alpha>\beta .$ If $\mathrm{a}_{\mathrm{n}}=\alpha^{\mathrm{n}}-\beta^{\mathrm{n}}$ for $\mathrm{n} \geq 1,$ then the value of $\frac{\mathrm{a}_{10}-2 \mathrm{a}_{8}}{2 \mathrm{a}_{9}}$ is (A) 1              (B) 2             (C) 3             (D) 4 [JEE 2011]
Ans. (C)
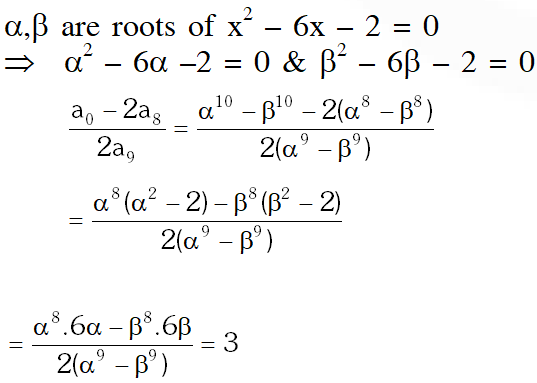
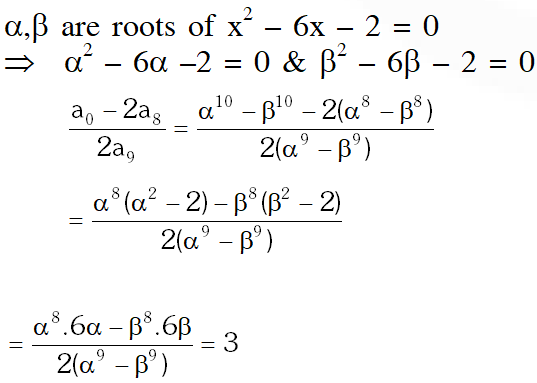
Q. A value of b for which the equations $\mathrm{x}^{2}+\mathrm{bx}-1=0$ $\mathrm{x}^{2}+\mathrm{x}+\mathrm{b}=0$ have one root in common is – (A) $-\sqrt{2}$ (B) $-i \sqrt{3}$ (C) $\mathrm{i} \sqrt{5}$ (D) $\sqrt{2}$ [JEE 2011]
Ans. (B)
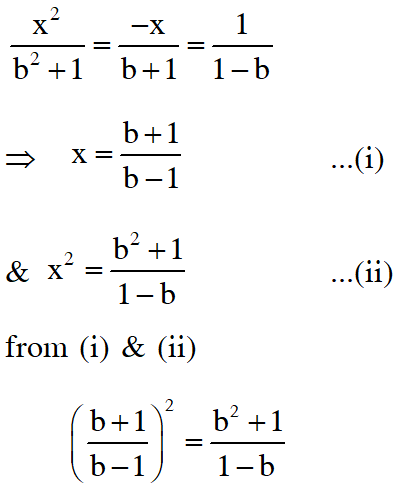
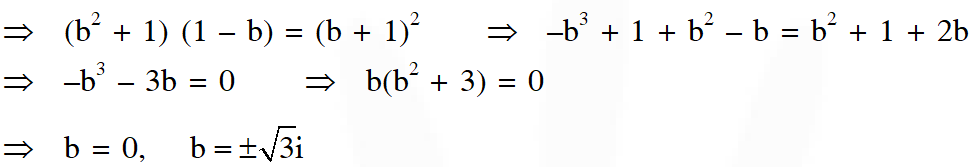
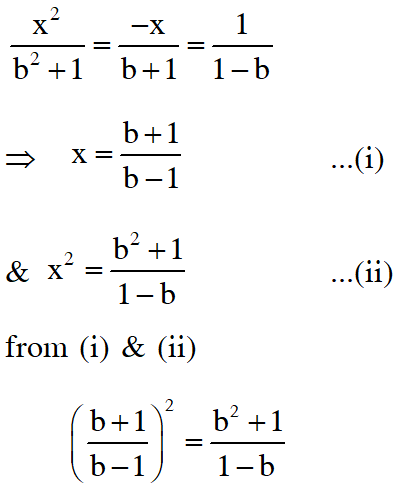
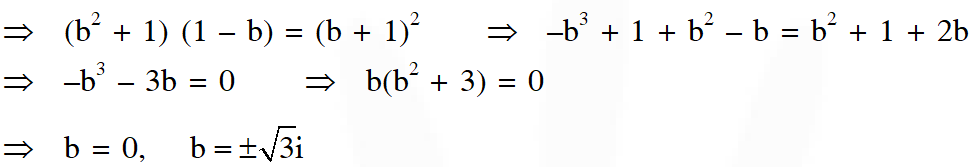
Q. Let S be the set of all non-zero numbers a such that the quadratic equation $\alpha \mathrm{x}^{2}$ – x + a = 0 has two distinct real roots $\mathrm{x}_{1}$ and $\mathrm{x}_{2}$ satisfying the inequality $\left|x_{1}-x_{2}\right|<1$. Which of the following intervals is(are) a subset(s) of S ? (A) $\left(-\frac{1}{2},-\frac{1}{\sqrt{5}}\right)$ (B) $\left(-\frac{1}{\sqrt{5}}, 0\right)$ (C) $\left(0, \frac{1}{\sqrt{5}}\right)$ (D) $\left(\frac{1}{\sqrt{5}}, \frac{1}{2}\right)$ [JEE 2015, 4M, –0M]
Ans. (A,D)
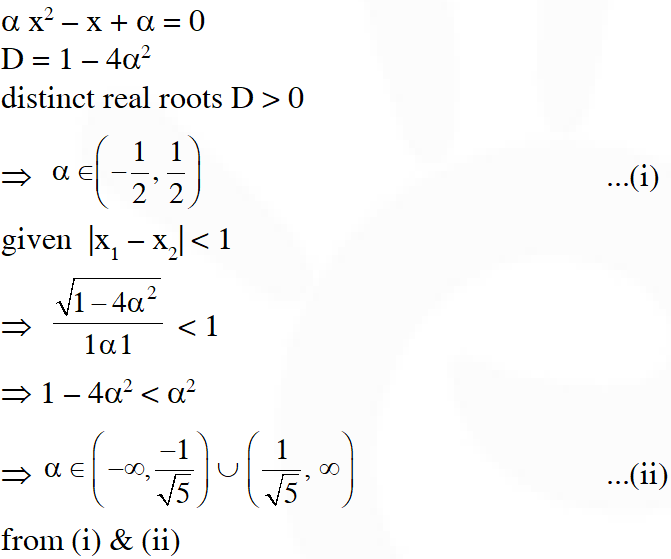
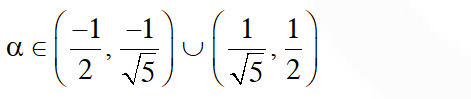
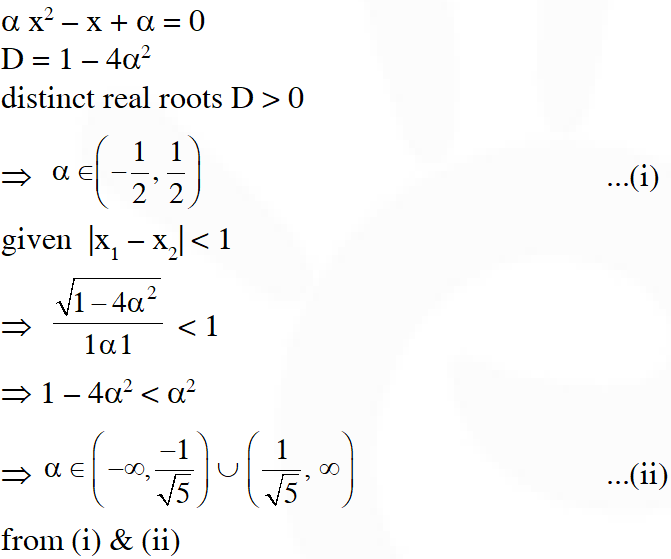
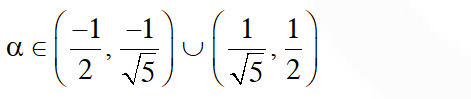
Q. Let $-\frac{\pi}{6}<\theta<-\frac{\pi}{12}$. Suppose $\alpha_{1}$ and $\beta_{1}$ are the roots of the equation $\mathrm{x}^{2}-2 \mathrm{xsec} \theta+1=0$ and $\alpha_{2}$ and $\beta_{2}$ are the roots of the equation $\mathrm{x}^{2}+2 \mathrm{xtan} \theta-1=0$. If $\alpha_{1}>\beta_{1}$ and $\alpha_{2}>\beta_{2},$ then $\alpha_{1}+\beta_{2}$ equals (A) $2(\sec \theta-\tan \theta)$ (B) $2 \sec \theta$ (C) $-2 \tan \theta$ (D) 0 [JEE(Advanced)-2016, 3(–1)]
Ans. (C)
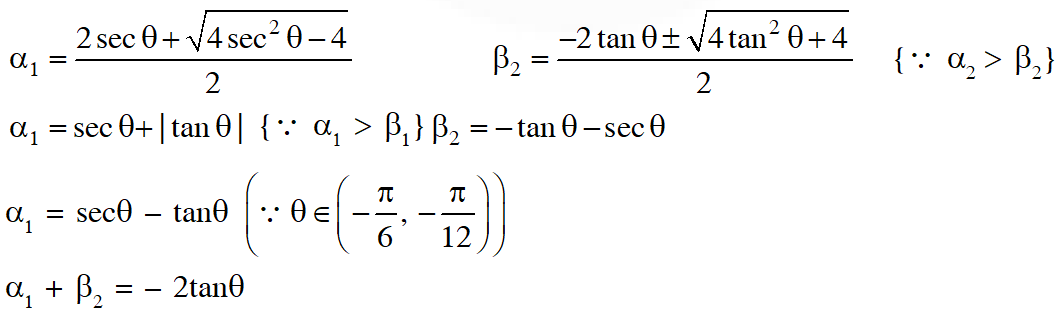
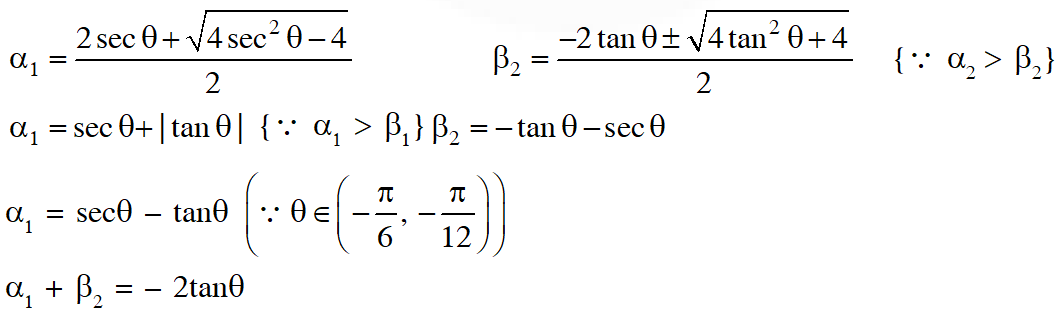
PARAGRAPH 2 Let p,q be integers and let $\alpha, \beta$ be the roots of the equation, $x^{2}-x-1=0,$ where $\alpha \neq \beta .$ For $n=0,1,2, \ldots . .,$ let $a_{n}=p \alpha^{n}+q \beta^{n}$. FACT : If a and b are rational numbers and $a+b \sqrt{5}=0,$ then $a=0=b$.
Q. If $a_{4}=28,$ then $p+2 q=$ (A) 14 (B) 7 (C) 12 (D) 21 [JEE(Advanced 2017, 3(–1)]
Ans. (C)
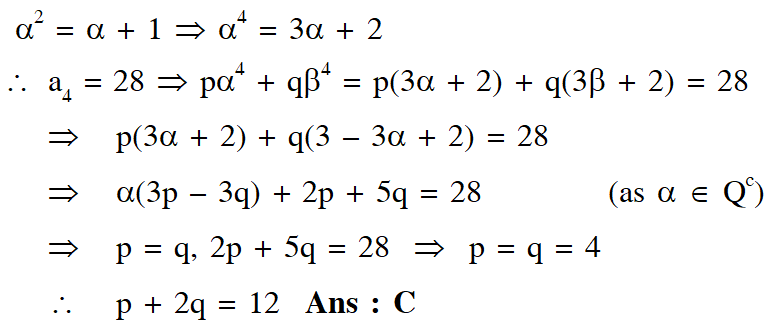
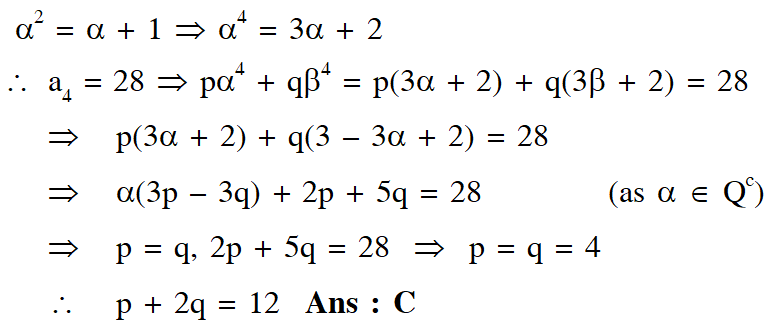
Q. $\mathrm{a}_{12}=$ (A) $2 \mathrm{a}_{11}+\mathrm{a}_{10}$ (B) $a_{11}-a_{10}$ (C) $\mathrm{a}_{11}+\mathrm{a}_{10}$ (D) $a_{11}+2 a_{10}$ [JEE(Advanced 2017, 3(–1)]
Ans. (C)

Frequently Asked Questions

Find answers to common questions.

How many quadratic equation questions appear in JEE Advanced each year?

Typically one to two questions on Quadratic Equations appear per JEE Advanced paper. Between 2009 and 2017, eight questions appeared across all papers. The topic is not guaranteed every year, but its overlap with complex numbers and sequences makes it high-priority revision material.

What is the weightage of Quadratic Equations in JEE Advanced Mathematics?

Quadratic Equations carries roughly 4–8% weightage in JEE Advanced Mathematics when you include its overlap with complex numbers and sequences. It is not the highest-weightage topic, but it is one of the most reliably solvable topics if prepared well, making it a strong source of definite marks.

Which JEE Advanced question on quadratic equations is considered the hardest?

The 2010 question (finding the quadratic with roots α/β and β/α given α+β = −p and α³+β³ = q) is widely considered the most algebraically demanding. It requires three separate Vieta manipulations in sequence and careful use of the constraint p³ ≠ ±q to avoid division-by-zero errors.

Do quadratic equation problems in JEE Advanced involve complex numbers?

Yes. At least two of the eight questions from 2009–2017 directly involve complex roots or complex values of parameters (notably the 2010 and 2011 common-root question). You cannot treat JEE Advanced quadratic preparation as purely real-number work — complex number fundamentals must be solid.

How is the recurrence relation approach used in JEE Advanced quadratic problems?

If α and β are roots of x² − bx − c = 0, then αⁿ satisfies αⁿ = b·αⁿ⁻¹ + c·αⁿ⁻². The sequence aₙ = pαⁿ + qβⁿ inherits the same recurrence. This appears directly in the 2011 Q1, 2017 Q1, and 2017 Q2 problems. Recognising this pattern instantly converts a hard problem into a simple substitution.


Leave a comment

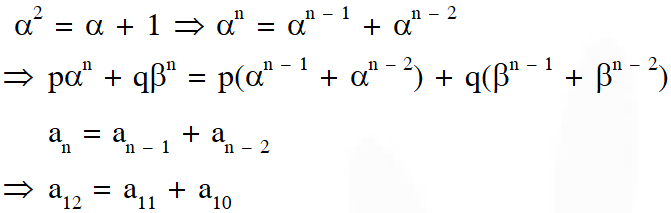
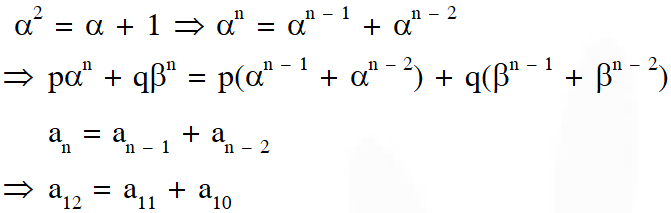
Comments

Yourmom
May 3, 2025, 6:35 a.m.
Very Easy! 😘
Delphia
Feb. 11, 2024, 12:34 a.m.
Wow, amazing blog layout! How long have you ever been running a blog for? you made blogging look easy. The full look of your website is fantastic, as well as the content material! You can see similar: Lunasolix.top and here Lunasolix.top
Inge
Feb. 6, 2024, 6:35 a.m.
Thank you, I've recently been searching for information about this topic for ages and yours is the greatest I have found out so far. However, what about the conclusion? Are you certain concerning the supply? silvoria.shop
Shiv
June 25, 2023, 6:35 a.m.
Sir upload more questions
BGMI LOVER
Feb. 5, 2023, 11:21 p.m.
Great questions I will suggest everyone to join E saral
Es
May 6, 2022, 6:49 p.m.
Tyyfyfdtyutrgreet Fgdgdgrwetrysr
Balamurugan
July 25, 2021, 10:59 a.m.
Sir one doubt if e = q/eo = [E] = rsinΦdΦ = q/eo = 4πr*2[e] = r = 14631m = 1/4π(14631)*8.85×10*-9f/m = 42.00479 Is this meaning of life sir
Vinit jangir
June 12, 2021, 2:29 p.m.
Sir my me is Vinit and I am taking lecture of Saransh sir and now I cracked jee advanced 2020 with self study and e saral YouTube videos got AIR 47
Jaat
May 19, 2023, 3:02 p.m.
Chutita kaat rha h
Aditya
June 28, 2024, 6:15 p.m.
Jaise tu hai
hi
May 12, 2021, 9:25 p.m.
awesome question
Keshav
May 11, 2021, 9:31 p.m.
Last one paragraph is best. But i am disappointed because there was only 7 or 8 question 😖. But thanks for that
Nitin jangid
April 26, 2021, 5:21 p.m.
Good question🙋🙋🙋
Divyansh Shrivastava
March 9, 2021, 5:03 p.m.
Thank You very much for these questions
GB
Oct. 19, 2020, 9:30 a.m.
Awesome questions
Yashwanth
Oct. 15, 2020, 10:19 p.m.
Really helpful and the solutions are really good and very concise.
Anish
Oct. 14, 2020, 10:47 a.m.
Really good
Vikas
Sept. 19, 2020, 4:58 p.m.
Really very helpful
sudharsan k
Sept. 14, 2020, 9:27 a.m.
pretty good and nice questions
Shruti Jain
Sept. 13, 2020, 7:45 a.m.
Good questions 👍👍
Abhinay
May 3, 2020, 10:30 p.m.
Excellent 👌👌👌
None

eSaral Gurukul

NEET

JEE Main

JEE Advanced

Our Telegram Channel

All Study Material