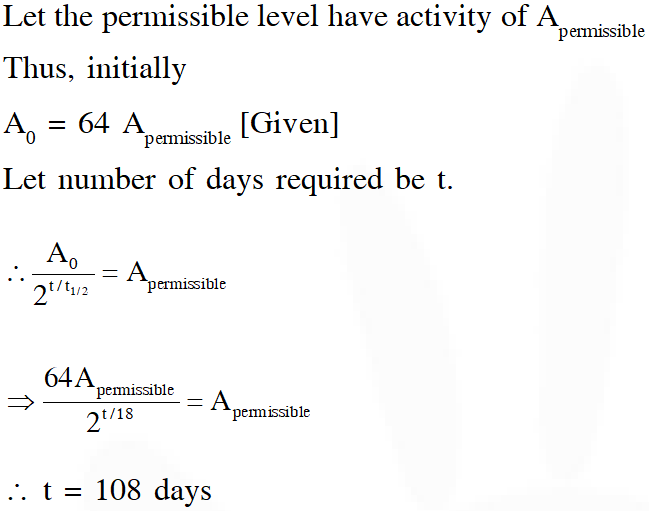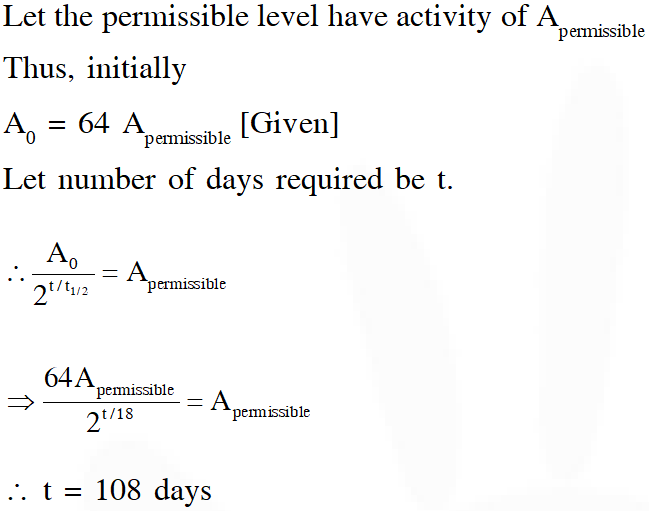JEE Advanced Previous Year Questions of Physics with Solutions are available at eSaral. Practicing JEE Advanced Previous Year Papers Questions of Physics will help the JEE aspirants in realizing the question pattern as well as help in analyzing weak & strong areas.
Get detailed Class 11th & 12th Physics Notes to prepare for Boards as well as competitive exams like IIT JEE, NEET etc.
eSaral helps the students in clearing and understanding each topic in a better way. eSaral is providing complete chapter-wise notes of Class 11th and 12th both for all subjects.
Click Here for JEE main Previous Year Topic Wise Questions of Physics with Solutions
Download eSaral app for free study material and video tutorials.
Simulator
Previous Years JEE Advanced Questions
Paragraph for Questions 3 and 4
The -decay process, discovered around 1900, is basically the decay of a neutron (n). In the laboratory, a proton (p) and an electron $\left(\mathrm{e}^{-}\right)$ are observed as the decay products of the neutron. Therefore, considering the decay of a neutron as a two-body decay process, it was predicted theoretically that the kinetic energy of the electron should be a constant. But experimentally, it was observed that the electron kinetic energy has a continuous spectrum. Considering a three-body decay process, $\mathrm{n} \rightarrow \mathrm{p}+\mathrm{e}^{-}+\vec{v}_{e}$ , around 1930, Pauli explained the observed electron energy spectrum. Assuming the anti-neutrino $\left(\vec{v}_{e}\right)$ to be massless and possessing negligible energy, and the neutron to be at rest, momentum and energy conservation principles are applied. From this calculation, the maximum kinetic energy of the electron is $0.8 \times 10^{6} \mathrm{eV}$ . The kinetic energy carried by the proton is only the recoil energy.
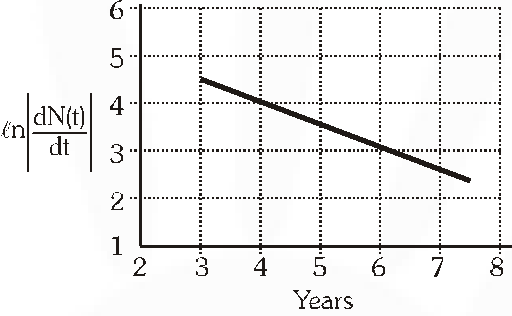
Q. To determine the half life of a radioactive element, a student plots a graph of $\ell n\left|\frac{d N(t)}{d t}\right|$ versus t. Here $\frac{d N(t)}{d t}$ is the rate of radioactive decay at time t. If the number of radioactive nuclei of this element decreases by a factor of p after 4.16 years, the value of p is ?
 [JEE- 2010]
[JEE- 2010]
 [JEE- 2010]
[JEE- 2010]
Ans. 8
$\left|\frac{\mathrm{d} \mathrm{N}}{\mathrm{dt}}\right|=\lambda \mathrm{N}_{0} \mathrm{e}^{-\lambda t} \therefore \operatorname{en}\left|\frac{\mathrm{d} \mathrm{N}}{\mathrm{dt}}\right|=\ln \left(\mathrm{N}_{0} \lambda\right)-\lambda \mathrm{t}$
$\therefore \ln \left|\frac{\mathrm{d} \mathrm{N}}{\mathrm{dt}}\right|=\ln \left(\mathrm{N}_{0} \lambda\right)-\lambda \mathrm{t} \Rightarrow-\lambda=\mathrm{slope}=-\frac{1}{2} \mathrm{year}^{-1}$
$\Rightarrow \lambda=\frac{1}{2} y r^{-1}$
$\therefore \mathrm{t}_{1 / 2}=\frac{0.693}{\lambda}=1.386$ given time is 3 times of $\mathrm{t}_{1 / 2}$
$\therefore$ value of $\mathrm{p}$ is 8
Q. The activity of a freshly prepared radioactive sample is $10^{10}$ disintegrations per second, whose mean life is $10^{9}$ s. The mass of an atom of this radioisotope is $10^{-25}$kg. The mass (in mg) of the radioactive sample is
[JEE-2011]
Ans. 1
$\mathrm{A}=\lambda \mathrm{N} \Rightarrow 10^{10}=\lambda \mathrm{N} \Rightarrow \mathrm{N}=\frac{10^{10}}{\lambda}=\left(10^{10}\right) \tau=10^{10} \times 10^{9}=10^{19}$
$\mathrm{M}=\mathrm{Nm}=\left(10^{19}\right)\left(10^{-25}\right)=10^{-6} \mathrm{kg}=1 \mathrm{mg}$
Q. If the anti-neutrino had a mass of $3 \mathrm{eV} / \mathrm{c}^{2}$ (where c is the speed of light) instead of zero mass, what should be the range of the kinetic energy, K, of the electron?
(A) $0 \leq K \leq 0.8 \times 10^{6} e V$
(B) $3.0 e V \leq K \leq 0.8 \times 10^{6} e V$
(C) $3.0 e V \leq K<0.8 \times 10^{6} e V$
(D) $0 \leq K<0.8 \times 10^{6} e V$
[JEE 2012]
Ans. (D)
Q. A freshly prepared sample of a radioisotope of half-life 1386 s has activity $10^{3}$ distintegrations per second. Given that n 2 = 0.693, the fraction of the initial number of nuclei (expressed in nearest integer percentage) that will decay in the first 80 s after preparation of the sample is.
[JEE Advance-2013]
Ans. 4
Given $\mathrm{T}_{1 / 2}=1386 \mathrm{sec}: ;\left|\frac{\mathrm{d} \mathrm{N}}{\mathrm{dt}}\right|=10^{3}$
fraction $=\frac{\mathrm{N}_{0}-\mathrm{N}}{\mathrm{N}_{0}}=\frac{\mathrm{N}_{0}-\mathrm{N}_{0} \mathrm{e}^{-\lambda \mathrm{t}}}{\mathrm{N}_{0}}=1-\mathrm{e}^{-\lambda \mathrm{t}}$
Q. A nuclear power plant supplying electrical power to a village uses a radioactive material of half life T years as the fuel. The amount of fuel at the beginning is such that the total power requirement of the village is 12.5% of the electrical power available from the plant at that time. If the plant is able to meet the total power needs of the village for a maximum period of nT years, then the value of n is.
[JEE Advance-2015]
Ans. 3
$12.5 \% \rightarrow\left(\frac{1}{8}\right)^{\mathrm{th}}$ of initial power
$\because$ After each $\mathrm{T},$ P will be half
$\mathrm{P} \stackrel{\mathrm{T}}{\longrightarrow} \frac{\mathrm{P}}{2} \stackrel{\mathrm{P}}{\longrightarrow} \frac{\mathrm{P}}{\longrightarrow} \stackrel{\mathrm{T}}{\longrightarrow} \frac{\mathrm{P}}{8}$
$\therefore$ Total time $=3 \mathrm{T}$
n = 3
Q. For a radioactive material, its activity A and rate of change of its activity R are defined as $A=-\frac{d N}{d t}$ and $\mathrm{R}=-\frac{\mathrm{d} \mathrm{A}}{\mathrm{dt}}$, where N(t) is the number of nuclei at time t. Two radioactive sources P (mean life $\tau$) and Q (mean life $2 \tau$) have the same activity at t = 0. Their rates of change of activities at t = $2 \tau$ are $\mathrm{R}_{\mathrm{p}}$ and $\mathrm{R}_{\mathrm{Q}}$, respectively. If $\frac{\mathrm{R}_{\mathrm{p}}}{\mathrm{R}_{\mathrm{Q}}}=\frac{\mathrm{n}}{\mathrm{e}}$, then the value of n is :
[JEE Advance-2015]
Ans.
$\mathrm{N}=\mathrm{N}_{0} \mathrm{e}^{-\lambda \mathrm{t}}$
$\mathrm{A}=\lambda \mathrm{N}_{0} \mathrm{e}^{-\lambda \mathrm{t}}$
$\mathrm{R}=\lambda^{2} \mathrm{N}_{0} \mathrm{e}^{-\lambda \mathrm{t}}$
$A_{P}=A_{Q}$ at $t=0$
$\lambda_{\mathrm{p}} \mathrm{N}_{\mathrm{p}} \mathrm{e}^{-\lambda \mathrm{Pt}}=\lambda_{0} \mathrm{N}_{\mathrm{o}} \mathrm{e}^{-\lambda \mathrm{Qt}}$ at $\mathrm{t}=0$
$\lambda_{\mathrm{p}} \mathrm{N}_{\mathrm{p}}=\lambda_{\mathrm{o}} \mathrm{N}_{\mathrm{O}} \quad \ldots$ (i)
$\frac{\mathrm{R}_{\mathrm{P}}}{\mathrm{R}_{\mathrm{Q}}}=\left(\frac{\lambda_{\mathrm{P}}}{\lambda_{\mathrm{Q}}}\right)^{2}\left(\frac{\mathrm{N}_{\mathrm{P}}}{\mathrm{N}_{\mathrm{Q}}}\right) \frac{\mathrm{e}^{-\lambda_{\mathrm{P}} 2 \tau}}{\mathrm{e}^{-\lambda_{\mathrm{Q}} 2 \tau}}$
$\frac{\mathrm{R}_{\mathrm{p}}}{\mathrm{R}_{\mathrm{Q}}}=\left(\frac{\lambda_{\mathrm{P}}}{\lambda_{\mathrm{Q}}}\right)^{2}\left(\frac{\mathrm{N}_{\mathrm{P}}}{\mathrm{N}_{\mathrm{Q}}}\right) \frac{1}{\mathrm{e}} \ldots$ (ii)
$\left[\lambda_{\mathrm{P}}=\frac{1}{\text { mean life }}\right]$
from equation (i) and equation (ii)
$\frac{\mathrm{R}_{\mathrm{P}}}{\mathrm{R}_{\mathrm{Q}}}=\frac{2}{\mathrm{e}}$
Ans. 2
Q. An accident in a nuclear laboratory resulted in deposition of a certain amount of radioactive material of half-life 18 days inside the laboratory. Tests revealed that the radiation was 64 times more than the permissible level required for safe operation of the laboratory. What is the minimum number of days after which the laboratory can be considered safe for use?
(A) 64 (B) 90 (C) 108 (D) 120
[JEE Advance-2016]
Ans.