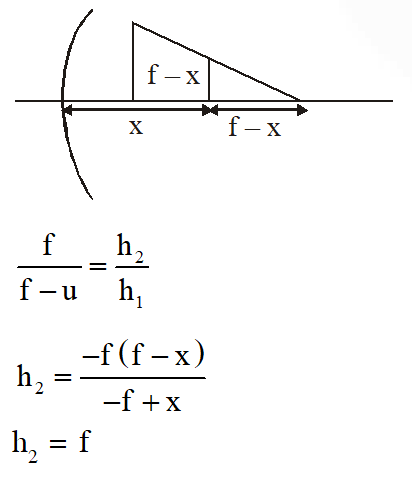JEE Advanced Previous Year Questions of Physics with Solutions are available at eSaral. Practicing JEE Advanced Previous Year Papers Questions of Physics will help the JEE aspirants in realizing the question pattern as well as help in analyzing weak & strong areas.
Get detailed Class 11th & 12th Physics Notes to prepare for Boards as well as competitive exams like IIT JEE, NEET etc.
eSaral helps the students in clearing and understanding each topic in a better way. eSaral is providing complete chapter-wise notes of Class 11th and 12th both for all subjects.
Click Here for JEE main Previous Year Topic Wise Questions of Physics with Solutions
Download eSaral app for free study material and video tutorials.
Simulator
Previous Years JEE Advanced Questions
Paragraph for Questions 12 and 13
Most materials have the refractive index, n>1. So, when a light ray from air enters a naturally occurring material, then by Snell's law, $\frac{\sin \theta_{1}}{\sin \theta_{2}}=\frac{n_{2}}{n_{1}}$ , it is understood that the refracted ray bends towards the normal. But it never emerges on the same side of the normal as the incident ray. According to electromagnetism, the refractive index of the medium is given by the relation, $n=\left(\frac{c}{v}\right)=\pm \sqrt{\varepsilon_{r} \mu_{r}}$ , where c is the speed of electromagnetic waves in vacuum, v its speed in the medium, $\varepsilon_{\mathrm{r}}$ and $\mu_{\mathrm{r}}$ are the relative permittivity and permeability of the medium respectively.
In normal materials, both $\varepsilon_{\mathrm{r}}$ and $\mu_{\mathrm{r}}$ are positive, implying positive n for the medium. When both $\varepsilon_{\mathrm{r}}$ and $\mu_{\mathrm{r}}$ are negative, one must choose the negative root of n. Such negative refractive index materials can now be artificially prepared and are called meta-materials. They exhibit significantly different optical behaviour, without violating any physical laws. Since n is negative, it results in a change in the direction of propagation of the refracted light. However, similar to normal materials, the frequency of light remains unchanged upon refraction even in meta materials.
Paragraph for Question No. 23 and 24
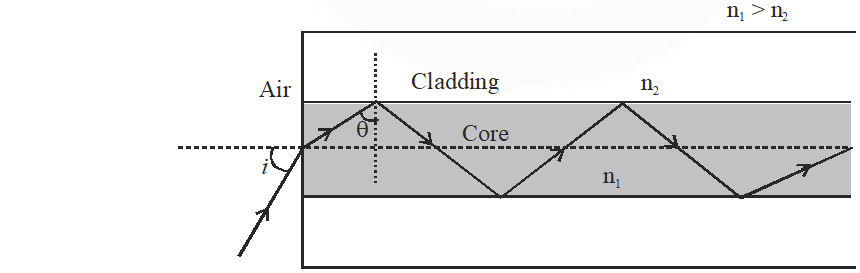
Light guidance in an optical fiber can be understood by considering a structure comprising of thin solid glass cylinder of refractive index $\mathbf{n}_{1}$ surrounded by a medium of lower refractive index $\mathrm{n}_{2}$. The light guidance in the structure takes place due to successive total internal reflections at the interface of the media $\mathbf{n}_{1}$ and $\mathrm{n}_{2}$ as shown in the figure. All rays with the angle of incidence i less than a particular value of $\dot{l}_{\mathrm{m}}$ are confined in the medium of refractive index $\mathrm{n}_{1}$. The numerical aperture (NA) of the structure is defined as sin $i_{\mathrm{m}}$.
Q. A ball is dropped from a height of 20 m above the surface of water in a lake. The refractive index of water is 4/3. A fish inside the lake, in the line of fall of the ball, is looking at the ball. At an instant, when the ball is 12.8 m above the water surface, the fish sees the speed of ball as $\left[\mathrm{g}=10 \mathrm{m} / \mathrm{s}^{2} .\right]$
(A) 9 m/s (B) 12 m/s (C) 16 m/s (D) 21.33 m/s
[IIT-JEE 2009]
Ans. (C)
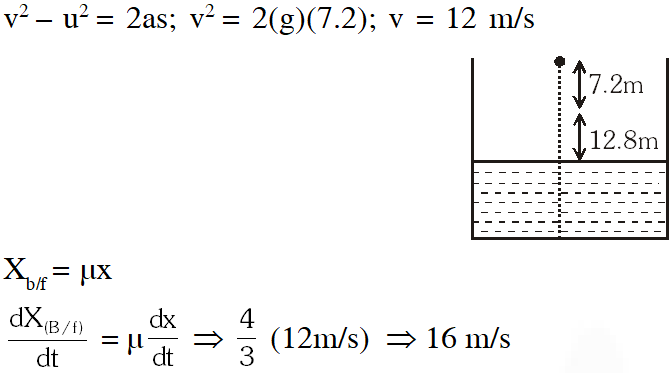
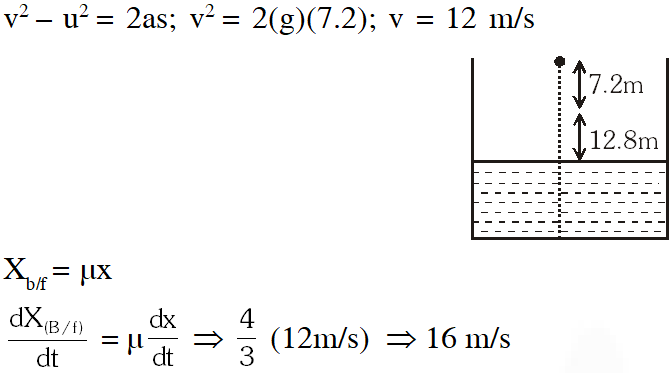
Q. A student performed the experiment of determination of focal length of a concave mirror by u-v method using an optical bench of length 1.5 m. The focal length of the mirror used is 24 cm. The maximum error in the location of the image can be 0.2 cm. The 5 sets of (u, v) values recorded by the student (in cm) are : (42, 56), (48, 48), (60, 40), (66, 33), (78, 39). The data set(s) that cannot come from experiment and is (are) incorrectly recorded, is (are) :
(A) (42, 56) (B) (48, 48) (C) (66, 33) (D) (78, 39)
[IIT-JEE 2009]
Ans. (C,D)
$\mathrm{V}=\frac{\mathrm{uf}}{\mathrm{u}-\mathrm{f}} \quad$ by sustituting the value of u and $\mathrm{f}$
$\mathrm{V}_{42} \Rightarrow \frac{24 \times 42}{18} \Rightarrow 56 ; \quad \mathrm{V}_{60}=\frac{24 \times 60}{36} \Rightarrow 40$
$\mathrm{v}_{48} \Rightarrow \frac{48 \times 24}{24} \Rightarrow 48 ; \mathrm{V}_{66}=\frac{66 \times 24}{42} \Rightarrow 37.71$
$\mathrm{V}_{78} \Rightarrow \frac{78 \times 24}{54} \Rightarrow 34.3$
(66, 33) ; (78, 39)
Q. A biconvex lens of focal length 15 cm is in front of a plane mirror. The distance between the lens and the mirror is 10 cm. A small object is kept at a distance of 30 cm from the lens. The final image is –
(A) virtual and at a distance of 16 cm from the mirror
(B) real and at a distance of 16 cm from the mirror
(C) virtual and at a distance of 20 cm from the mirror
(D) real and at a distance of 20 cm from the mirror
[IIT-JEE 2010]
Ans. (B)
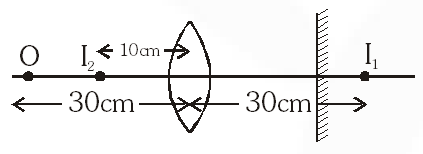 $\frac{1}{15}=\frac{1}{v}-\frac{1}{10}$
$\frac{1}{15}=\frac{1}{v}-\frac{1}{10}$
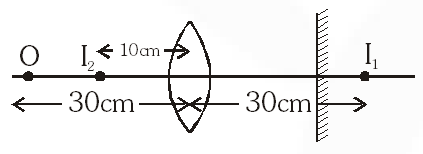 $\frac{1}{15}=\frac{1}{v}-\frac{1}{10}$
$\frac{1}{15}=\frac{1}{v}-\frac{1}{10}$
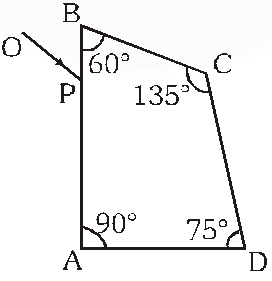
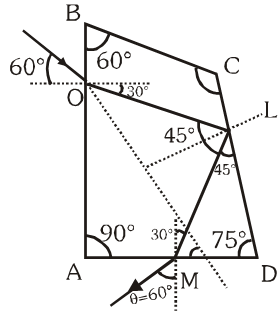
Q. A ray OP of monochromatic light is incident on the face AB of prism ABCD near vertex B at an incident angle of $60^{\circ}$ (see figure). If the refractive index of the material of the prism is $\sqrt{3}$, which of the following is (are) correct?
(A) The ray gets totally internally reflected at face CD
(B) The ray comes out through face AD
(C) The angle between the incident ray and the emergent ray is $90^{\circ}$
(D) The angle between the incident ray and the emergent ray is $120^{\circ}$
 [IIT-JEE 2010]
[IIT-JEE 2010]
 [IIT-JEE 2010]
[IIT-JEE 2010]
Ans. (A,B,C)
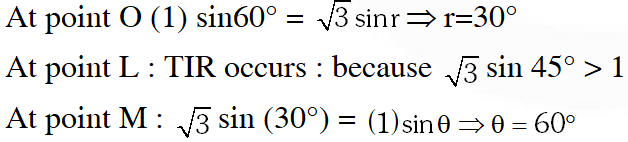

Q. Two transparent media of refractive indices $\mu_{1}$ and $\mu_{3}$ have a solid lens shaped transparent material of refractive index $\mu_{2}$ between them as shown in figures in Column II. A ray traversing these media is also shown in the figures. In Column I different relationships between $\mu_{1}, \mu_{2}$ and $\mu_{3}$ are given. Match them to the ray diagrams shown in Column II.

 [IIT-JEE 2010]
[IIT-JEE 2010]

 [IIT-JEE 2010]
[IIT-JEE 2010]
Ans. $(\mathrm{A})-\mathrm{pr},(\mathrm{B})-\mathrm{qst},(\mathrm{C})-\mathrm{prt},(\mathrm{D})-\mathrm{qs}$
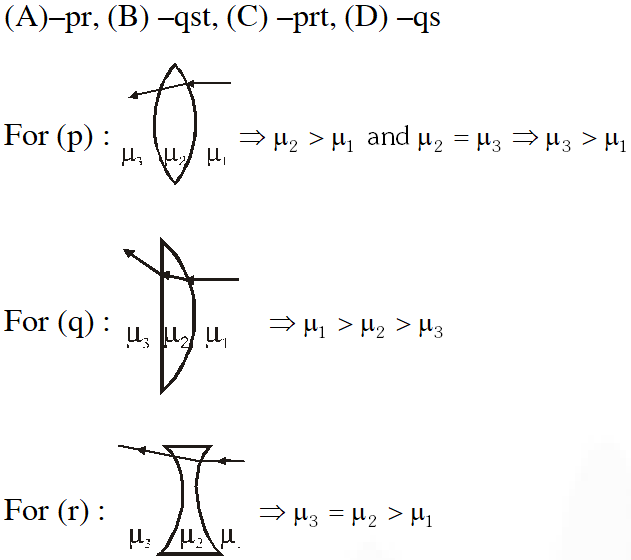
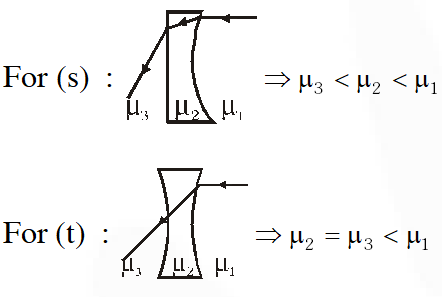
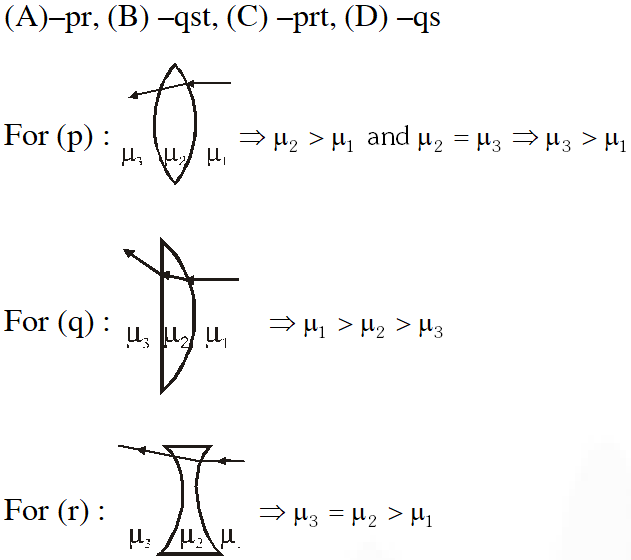
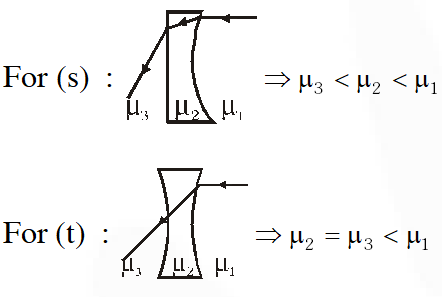
Q. The focal length of a thin biconvex lens is 20 cm. When an object is moved from a distance of 25 cm in front of it to 50 cm, the magnification of its image changes from $\mathrm{m}_{25}$ to $\mathrm{m}_{50} .$ The ratio $\frac{m_{25}}{m_{50}}$ is -
[IIT-JEE 2010]
Ans. 6
$\mathrm{m}=\frac{\mathrm{f}}{\mathrm{f}+\mathrm{u}}$
Q. Image of an object approaching a convex mirror of radius of curvature 20 m along its optical axis is observed to move from $\frac{25}{3}$ m to $\frac{50}{7}$ m in 30 seconds. What is the speed of the object in km per hour ?
[IIT-JEE 2010]
Ans. 3
$\frac{1}{f}=\frac{1}{u}+\frac{1}{v} \Rightarrow \frac{1}{10}=\frac{1}{u}+\frac{3}{25} \Rightarrow u=-50 \mathrm{m}$
$\frac{1}{\mathrm{f}}=\frac{1}{\mathrm{u}}+\frac{1}{\mathrm{v}} \Rightarrow \frac{1}{10}=\frac{1}{\mathrm{u}}+\frac{7}{50} \Rightarrow \mathrm{u}=-25 \mathrm{m}$
Speed $=\frac{25}{30} \times \frac{18}{5}=3$
Q. A large glass slab $\left(\mu=\frac{5}{3}\right)$ of thickness 8 cm is placed over a point source of light on a plane surface. It is seen that light emerges out of the top surface of the slab from a circular area of radius R cm. What is the value of R?
[IIT-JEE 2010]
Ans. 6
$r=\frac{h}{\sqrt{\mu^{2}-1}}=\frac{8}{\sqrt{\left(\frac{5}{3}\right)^{2}-1}}=6 \mathrm{cm}$
Q. A light ray traveling in glass medium is incident on glass-air interface at an angle of incidence $\theta$. The reflected (R) and transmitted (T) intensities, both as function of $\theta$, are plotted. The correct sketch is –
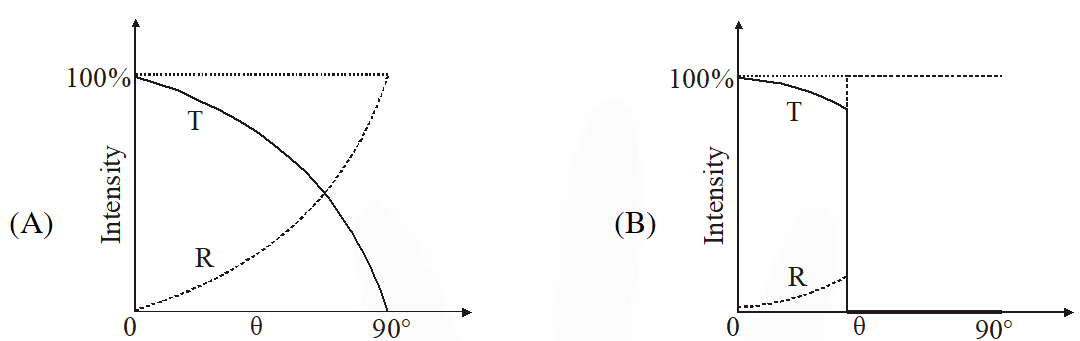
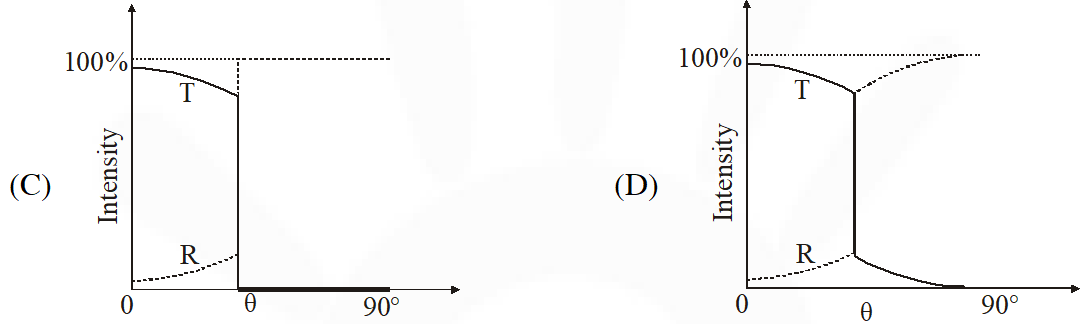 [IIT-JEE 2011]
[IIT-JEE 2011]
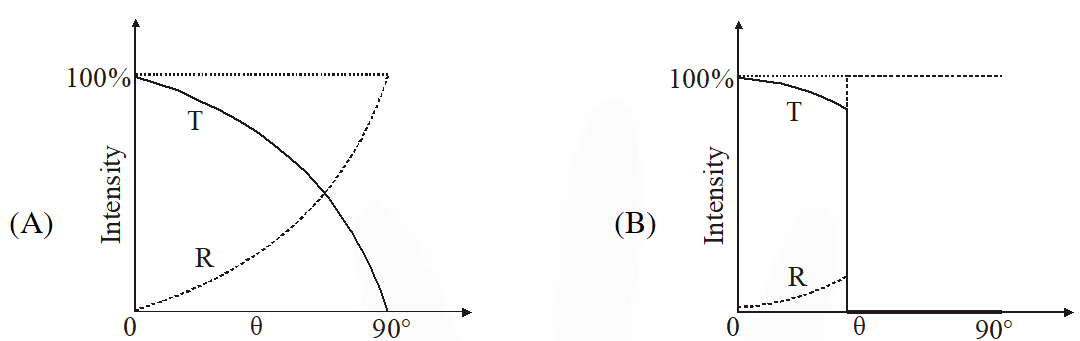
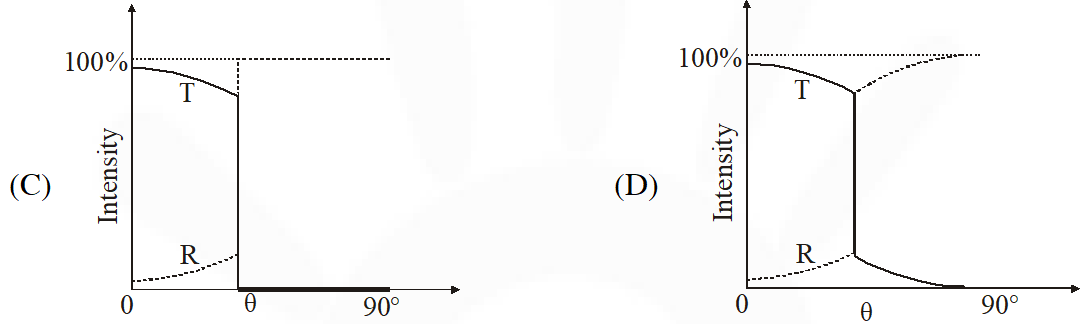 [IIT-JEE 2011]
[IIT-JEE 2011]
Ans. (C)
When $\theta=0^{\circ},$ maximum light is transmitted. At $\theta>\theta_{\mathrm{C}}$ (critical angle), no further light is transmitted
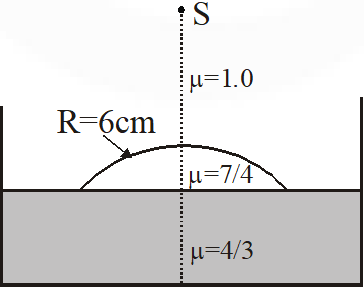
Q. Water (with refractive index = $\frac{4}{3}$) in a tank is 18 cm deep. Oil of refractive index $\frac{7}{4}$ lies on water making a convex surface of radius of curvature ‘R = 6 cm’ as shown. Consider oil to act as a thin lens. An object ‘S’ is placed 24 cm above water surface. The location of its image is at ‘x’ cm above the bottom of the tank. Then ‘x’ is
 [IIT-JEE 2011]
[IIT-JEE 2011]
 [IIT-JEE 2011]
[IIT-JEE 2011]
Ans. 2
First refraction [ Lens-air interface]
$\frac{\mu_{2}}{v}-\frac{\mu_{1}}{u}=\frac{\mu_{2}-\mu_{1}}{R}$ where $\mu_{1}=1, \mathrm{u}=-24, \mu_{2}=\frac{7}{4}, \mathrm{R}=+6$
After solving v = 21
Now for second refraction [Lens-water interface]
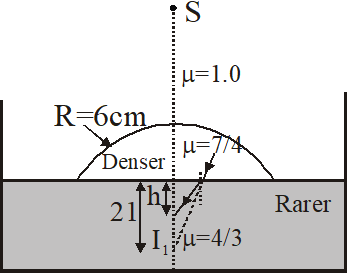 $\frac{4 / 3}{v_{2}}-\frac{7 / 4}{21}=0 \Rightarrow v_{2}=h=16 \mathrm{cm}$
So, from bottom $18-16=2 \Rightarrow \mathrm{x}=2$
$\frac{4 / 3}{v_{2}}-\frac{7 / 4}{21}=0 \Rightarrow v_{2}=h=16 \mathrm{cm}$
So, from bottom $18-16=2 \Rightarrow \mathrm{x}=2$
 $\frac{4 / 3}{v_{2}}-\frac{7 / 4}{21}=0 \Rightarrow v_{2}=h=16 \mathrm{cm}$
So, from bottom $18-16=2 \Rightarrow \mathrm{x}=2$
$\frac{4 / 3}{v_{2}}-\frac{7 / 4}{21}=0 \Rightarrow v_{2}=h=16 \mathrm{cm}$
So, from bottom $18-16=2 \Rightarrow \mathrm{x}=2$
Q. A biconvex lens is formed with two thin plano-convex lenses as shown in the figure, Refractive index n of the first lens is 1.5 and that of the second lens is 1.2. Both the curved surfaces are of the same radius of curvature R = 14 cm. For this biconvex lens, for an object distance of 40 cm, the image distance will be :-
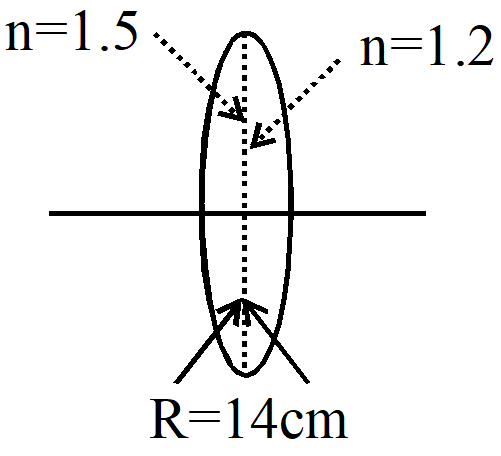 (A) –280.0 cm (B) 40.0 cm (C) 21.5 cm (D) 13.3 cm
[IIT-JEE 2012]
(A) –280.0 cm (B) 40.0 cm (C) 21.5 cm (D) 13.3 cm
[IIT-JEE 2012]
 (A) –280.0 cm (B) 40.0 cm (C) 21.5 cm (D) 13.3 cm
[IIT-JEE 2012]
(A) –280.0 cm (B) 40.0 cm (C) 21.5 cm (D) 13.3 cm
[IIT-JEE 2012]
Ans. (B)
$\frac{1}{\mathrm{f}}=\frac{1}{\mathrm{f}_{1}}+\frac{1}{\mathrm{f}_{2}}$
$\frac{1}{\mathrm{f}}=\left(\frac{\mu_{1}-1}{\mathrm{R}_{1}}\right)+\left(\frac{\mu_{2}-1}{\mathrm{R}_{2}}\right) \Rightarrow \frac{1}{\mathrm{f}}=\frac{5}{14}+\frac{2}{14}$
f = 20 c.m.
$\frac{1}{\mathrm{v}}-\frac{1}{\mathrm{u}}=\frac{1}{\mathrm{f}} \Rightarrow \frac{1}{\mathrm{v}}-\frac{1}{-40}=\frac{1}{20}=40 \mathrm{c.m}$
Q. For light incident from air on a meta-material, the appropriate ray diagram is –
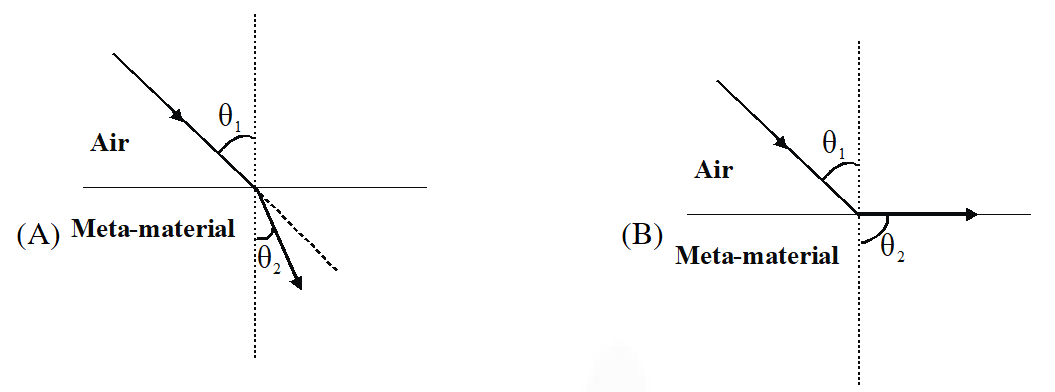
 [IIT-JEE 2012]
[IIT-JEE 2012]
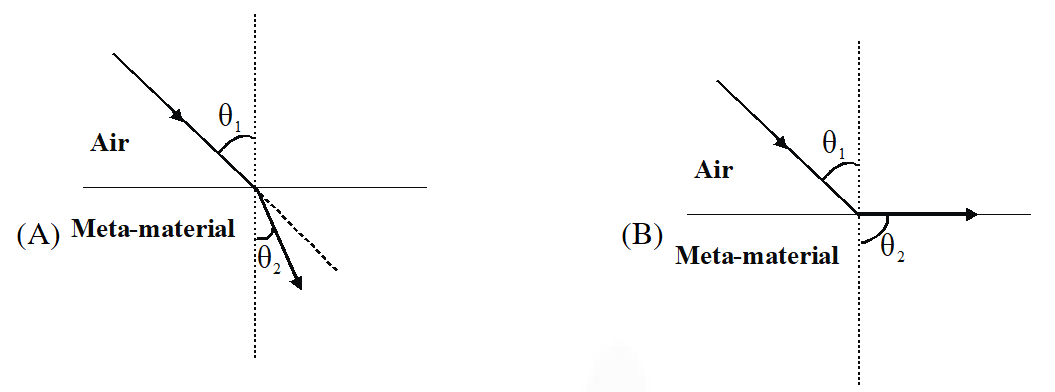
 [IIT-JEE 2012]
[IIT-JEE 2012]
Ans. (C)
$_{1} \mu_{2}=\frac{\mu_{2}}{\mu_{1}}=\frac{\sin \mathrm{i}}{\sin \mathrm{r}}$
$\frac{(-)}{1}=\frac{\sin \mathrm{i}}{\sin \mathrm{r}}$
sini = sin(–r)
Q. Choose the correct statement.
(A) The speed of light in the meta-material is $\mathrm{v}=\mathrm{c}|\mathrm{n}|$
(B) The speed of light in the meta-material is v = $\frac{c}{|n|}$
(C) The speed of light in the meta-material is v = c.
(D) The wavelength of the light in the meta-material $\left(\lambda_{\mathrm{m}}\right)$ is given by $\lambda_{\mathrm{m}}=\lambda_{\mathrm{air}}|\mathrm{n}|,$ where $\lambda_{\mathrm{air}}$ is the wavelength of the light in air.
[IIT-JEE 2012]
Ans. (B)
$\mu=\frac{\mathrm{c}}{\mathrm{v}} \Rightarrow \mathrm{v}=\frac{\mathrm{c}}{\mu}=\frac{\mathrm{c}}{\mathrm{n}}$
Q. A ray of light travelling in the direction $\frac{1}{2}(\hat{i}+\sqrt{3} \hat{j})$ is incident on a plane mirror. After reflection, it travels along the direction $\frac{1}{2}(\hat{i}-\sqrt{3} \hat{j})$. The angle of incidence is :-
(A) $30^{\circ}$
(B) $45^{\circ}$
(C) $60^{\circ}$
(D) $75^{\circ}$
[JEE-Advance-2013]
Ans. (A)
Here normal is along $\hat{j}$
Angle between incident ray and normal $\cos \theta=\frac{\frac{1}{2}(\hat{i}+\sqrt{3} \hat{j}) \cdot \hat{j}}{(1)(1)}=\frac{\sqrt{3}}{2} \Rightarrow \theta=30^{\circ}$
Q. The image of an object, formed by a plano-convex lens at a distance of 8 m behind the lens, is real and is one-third the size of the object. The wavelength of light inside the lens is $\frac{2}{3}$ times the wavelength in free space. The radius of the curved surface of the lens is :
(A) 1 m (B) 2 m (C) 3 m (D) 6 m
[JEE-Advance-2013]
Ans. (C)
$\mathrm{m}=-\frac{1}{3}=\frac{\mathrm{v}}{\mathrm{u}}$
v = 8m
u = – 24 m
$\frac{1}{\mathrm{v}}-\frac{1}{\mathrm{u}}=\frac{1}{\mathrm{f}} \rightarrow \frac{1}{8}-\frac{1}{-24}=\frac{1}{\mathrm{f}} \Rightarrow \mathrm{f}=6 \mathrm{m}$
$\mathrm{f}=\frac{\mathrm{R}}{(\mu-1)}$
$\mu=\frac{\lambda_{\text {vaceum }}}{\lambda_{\text {medium }}}=\frac{3}{2}$
$6 \mathrm{m}=\left(\frac{\mathrm{R}}{3 / 2-1}\right) \Rightarrow \mathrm{R}=3 \mathrm{m}$
Q. A right angled prism of refractive index $\mu_{1}$ is placed in a rectangular block of refractive index $\mu_{2}$, which is surrounded by a medium of refractive index $\mu_{3}$, as shown in the figure. A ray of light 'e' enters the rectangular block at normal incidence. Depending upon the relationships between $\mu_{1}, \mu_{2},$ and $\mu_{3}$, it takes one of the four possible paths 'ef', 'eg', 'eh' or 'ei'.
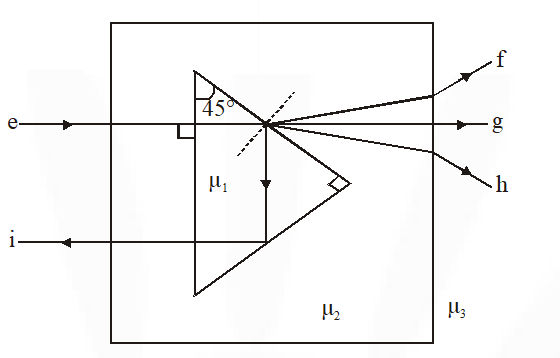 Match the paths in List I with conditions of refractive indices in List II and select the correct answer using the codes given below the lists :
Match the paths in List I with conditions of refractive indices in List II and select the correct answer using the codes given below the lists :
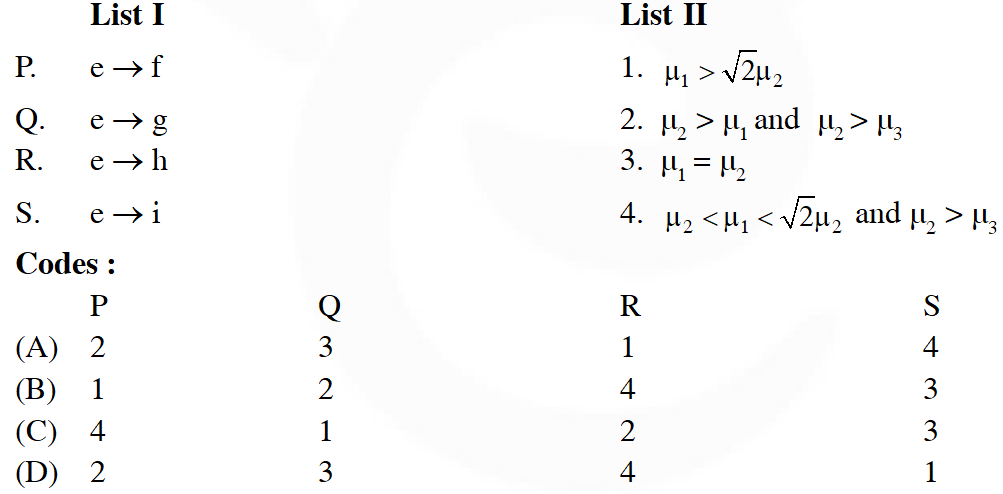 [JEE-Advance-2013]
[JEE-Advance-2013]
 Match the paths in List I with conditions of refractive indices in List II and select the correct answer using the codes given below the lists :
Match the paths in List I with conditions of refractive indices in List II and select the correct answer using the codes given below the lists :
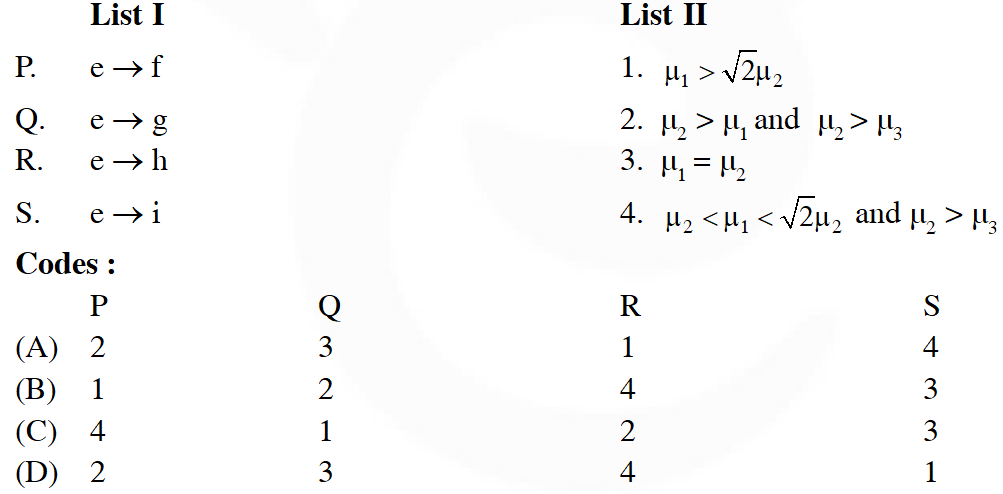 [JEE-Advance-2013]
[JEE-Advance-2013]
Ans. (D)
(P) at prism surface ray moving towards normal so $\left(\mu_{2}>\mu_{1}\right)$at block surface ray moving away from normal so $\left(\mu_{3}<\mu_{2}\right)$
(Q) No deflection of ray on both surface; so $\mu_{1}=\mu_{2}=\mu_{3}$
(R) At prism surface ray moving away from normal so $\mu_{2}<\mu_{1}$. At block surface ray movign away from normal so µ3 < µ2 but since on total internal reflection not takes place on prism surface
$\mu_{1} \sin 45^{\circ}<\mu_{2} \sin 90^{\circ} \Rightarrow \mu_{1}<\sqrt{2} \mu_{2}$
(S) Total internal reflection takes place so $\mu_{1} \sin 45^{\circ}>\mu_{2} \sin 90^{\circ} \Rightarrow \mu_{1}>\sqrt{2} \mu_{2}$
Q. A transparent thin film of uniform thickness and refractive index $\mathrm{n}_{1}=1.4$ is coated on the convex spherical surface of radius R at one end of a long solid glass cylinder of refractive index $\mathrm{n}_{2}=1.5$, as shown in the figure. Rays of light parallel to the axis of the cylinder traversing through the film from air to glass get focused at distance $\mathrm{f}_{1}$ from the film, while rays of light traversing from glass to air get focused at distance $\mathrm{f}_{2}$ from the film. Then
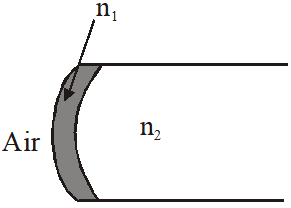 $(\mathrm{A})\left|\mathrm{f}_{1}\right|=3 \mathrm{R}$
(B) $\left|\mathrm{f}_{1}\right|=2.8 \mathrm{R}$
(C) $\left|\mathrm{f}_{2}\right|=2 \mathrm{R}$b
$(\mathrm{D})\left|\mathrm{f}_{2}\right|=1.4 \mathrm{R}$
[JEE-Advance-2014]
$(\mathrm{A})\left|\mathrm{f}_{1}\right|=3 \mathrm{R}$
(B) $\left|\mathrm{f}_{1}\right|=2.8 \mathrm{R}$
(C) $\left|\mathrm{f}_{2}\right|=2 \mathrm{R}$b
$(\mathrm{D})\left|\mathrm{f}_{2}\right|=1.4 \mathrm{R}$
[JEE-Advance-2014]
 $(\mathrm{A})\left|\mathrm{f}_{1}\right|=3 \mathrm{R}$
(B) $\left|\mathrm{f}_{1}\right|=2.8 \mathrm{R}$
(C) $\left|\mathrm{f}_{2}\right|=2 \mathrm{R}$b
$(\mathrm{D})\left|\mathrm{f}_{2}\right|=1.4 \mathrm{R}$
[JEE-Advance-2014]
$(\mathrm{A})\left|\mathrm{f}_{1}\right|=3 \mathrm{R}$
(B) $\left|\mathrm{f}_{1}\right|=2.8 \mathrm{R}$
(C) $\left|\mathrm{f}_{2}\right|=2 \mathrm{R}$b
$(\mathrm{D})\left|\mathrm{f}_{2}\right|=1.4 \mathrm{R}$
[JEE-Advance-2014]
Ans. (A,C)
When rays are moving from air to glass,
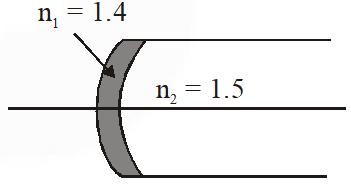 $\frac{1.5}{\mathrm{f}_{1}}=\frac{(1.4-1)}{+\mathrm{R}}+\frac{(1.5-1.4)}{+\mathrm{R}}$
$\frac{1.5}{\mathrm{f}_{1}}=\frac{0.4}{\mathrm{R}}+\frac{0.1}{\mathrm{R}}=\frac{0.5}{\mathrm{R}}$
$\left|\mathrm{f}_{1}\right|=3 \mathrm{R}$
When rays are moving from glass to air,
$\frac{1}{\mathrm{F}_{2}}=\frac{(1-1.4)}{-\mathrm{R}}+\frac{(1.4-1.5)}{-\mathrm{R}}=\frac{0.5}{\mathrm{R}}$
$\left|\mathrm{f}_{2}\right|=2 \mathrm{R}$
$\frac{1.5}{\mathrm{f}_{1}}=\frac{(1.4-1)}{+\mathrm{R}}+\frac{(1.5-1.4)}{+\mathrm{R}}$
$\frac{1.5}{\mathrm{f}_{1}}=\frac{0.4}{\mathrm{R}}+\frac{0.1}{\mathrm{R}}=\frac{0.5}{\mathrm{R}}$
$\left|\mathrm{f}_{1}\right|=3 \mathrm{R}$
When rays are moving from glass to air,
$\frac{1}{\mathrm{F}_{2}}=\frac{(1-1.4)}{-\mathrm{R}}+\frac{(1.4-1.5)}{-\mathrm{R}}=\frac{0.5}{\mathrm{R}}$
$\left|\mathrm{f}_{2}\right|=2 \mathrm{R}$
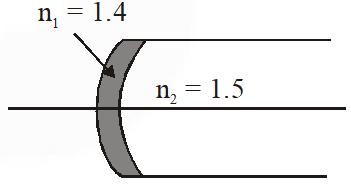 $\frac{1.5}{\mathrm{f}_{1}}=\frac{(1.4-1)}{+\mathrm{R}}+\frac{(1.5-1.4)}{+\mathrm{R}}$
$\frac{1.5}{\mathrm{f}_{1}}=\frac{0.4}{\mathrm{R}}+\frac{0.1}{\mathrm{R}}=\frac{0.5}{\mathrm{R}}$
$\left|\mathrm{f}_{1}\right|=3 \mathrm{R}$
When rays are moving from glass to air,
$\frac{1}{\mathrm{F}_{2}}=\frac{(1-1.4)}{-\mathrm{R}}+\frac{(1.4-1.5)}{-\mathrm{R}}=\frac{0.5}{\mathrm{R}}$
$\left|\mathrm{f}_{2}\right|=2 \mathrm{R}$
$\frac{1.5}{\mathrm{f}_{1}}=\frac{(1.4-1)}{+\mathrm{R}}+\frac{(1.5-1.4)}{+\mathrm{R}}$
$\frac{1.5}{\mathrm{f}_{1}}=\frac{0.4}{\mathrm{R}}+\frac{0.1}{\mathrm{R}}=\frac{0.5}{\mathrm{R}}$
$\left|\mathrm{f}_{1}\right|=3 \mathrm{R}$
When rays are moving from glass to air,
$\frac{1}{\mathrm{F}_{2}}=\frac{(1-1.4)}{-\mathrm{R}}+\frac{(1.4-1.5)}{-\mathrm{R}}=\frac{0.5}{\mathrm{R}}$
$\left|\mathrm{f}_{2}\right|=2 \mathrm{R}$
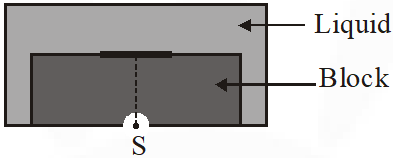
Q. A point source S is placed at the bottom of a transparent block of height 10 mm and refractive index 2.72. It is immersed in a lower refractive index liquid as shown in the figure. It is found that the light emerging from the block to the liquid forms a circular bright spot of diameter 11.54 mm on the top of the block. The refractive index of the liquid is :-
 (A) 1.21 (B) 1.30 (C) 1.36 (D) 1.42
[JEE-Advance-2014]
(A) 1.21 (B) 1.30 (C) 1.36 (D) 1.42
[JEE-Advance-2014]
 (A) 1.21 (B) 1.30 (C) 1.36 (D) 1.42
[JEE-Advance-2014]
(A) 1.21 (B) 1.30 (C) 1.36 (D) 1.42
[JEE-Advance-2014]
Ans. (C)
From the given situation, at critical angle,
$\tan \theta=\frac{(\mathrm{d} / 2)}{\mathrm{h}}=\frac{5.77}{10}$
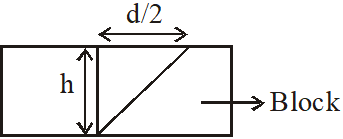 $\therefore \sin \theta_{\mathrm{C}} \approx \frac{1}{2}$
$\mu_{\text {denser }} \sin \theta_{\mathrm{C}}=\mu_{\text {raver }} \sin (\pi / 2)$
$\Rightarrow 2.72 \times \frac{1}{2}=\mu_{\mathrm{r}} \Rightarrow \mu_{\mathrm{r}}=1.36$
$\therefore \sin \theta_{\mathrm{C}} \approx \frac{1}{2}$
$\mu_{\text {denser }} \sin \theta_{\mathrm{C}}=\mu_{\text {raver }} \sin (\pi / 2)$
$\Rightarrow 2.72 \times \frac{1}{2}=\mu_{\mathrm{r}} \Rightarrow \mu_{\mathrm{r}}=1.36$
 $\therefore \sin \theta_{\mathrm{C}} \approx \frac{1}{2}$
$\mu_{\text {denser }} \sin \theta_{\mathrm{C}}=\mu_{\text {raver }} \sin (\pi / 2)$
$\Rightarrow 2.72 \times \frac{1}{2}=\mu_{\mathrm{r}} \Rightarrow \mu_{\mathrm{r}}=1.36$
$\therefore \sin \theta_{\mathrm{C}} \approx \frac{1}{2}$
$\mu_{\text {denser }} \sin \theta_{\mathrm{C}}=\mu_{\text {raver }} \sin (\pi / 2)$
$\Rightarrow 2.72 \times \frac{1}{2}=\mu_{\mathrm{r}} \Rightarrow \mu_{\mathrm{r}}=1.36$
Q. Four combinations of two thin lenses are given in List I. The radius of curvature of all curved surfaces is r and the refractive index of all the lenses is 1.5. Match lens combinations in List I with their focal length in List II and select the correct answer using the code given below the lists.
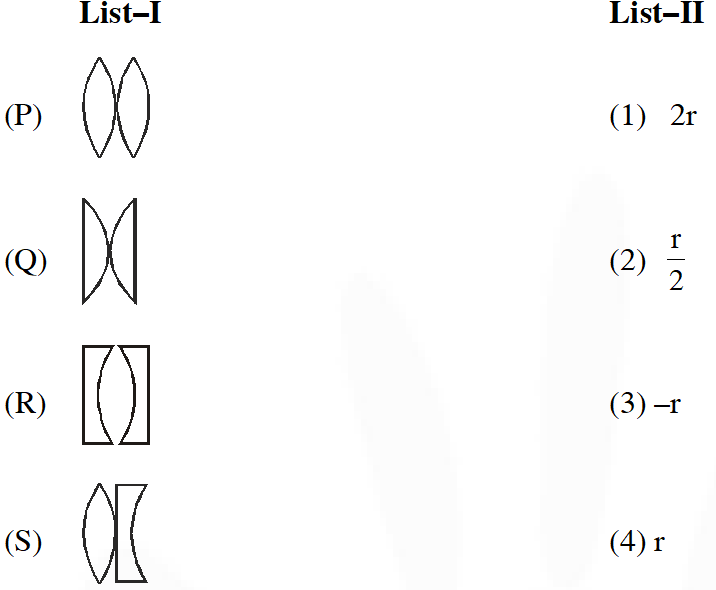
 [JEE-Advance-2014]
[JEE-Advance-2014]
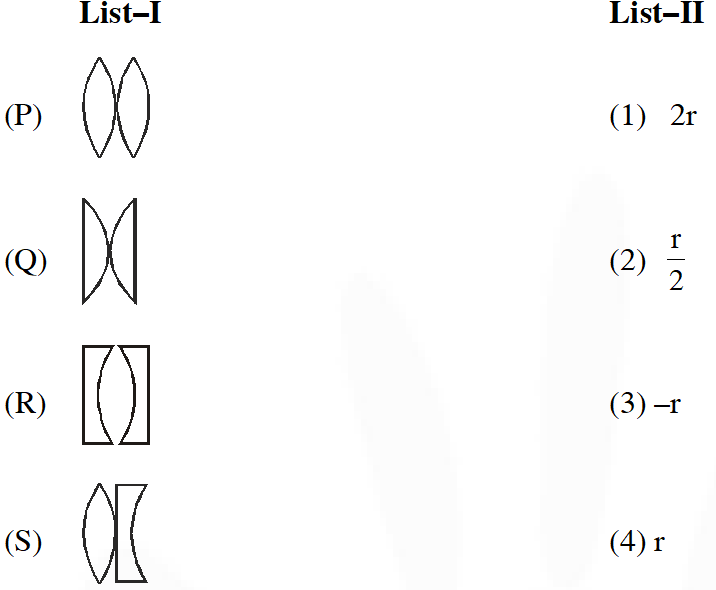
 [JEE-Advance-2014]
[JEE-Advance-2014]
Ans. (B)
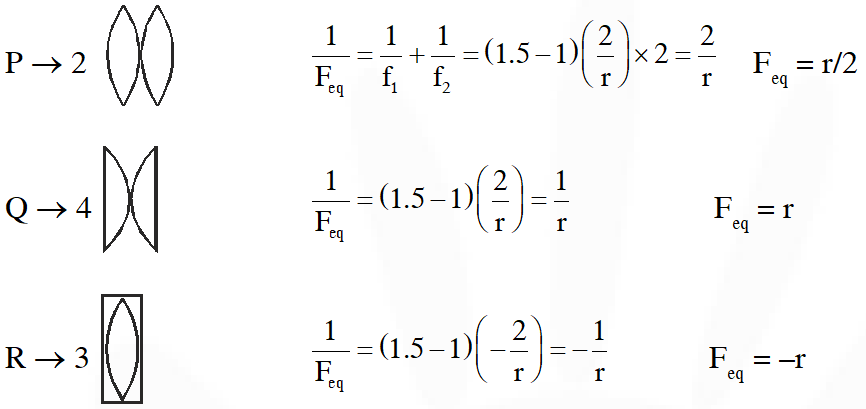
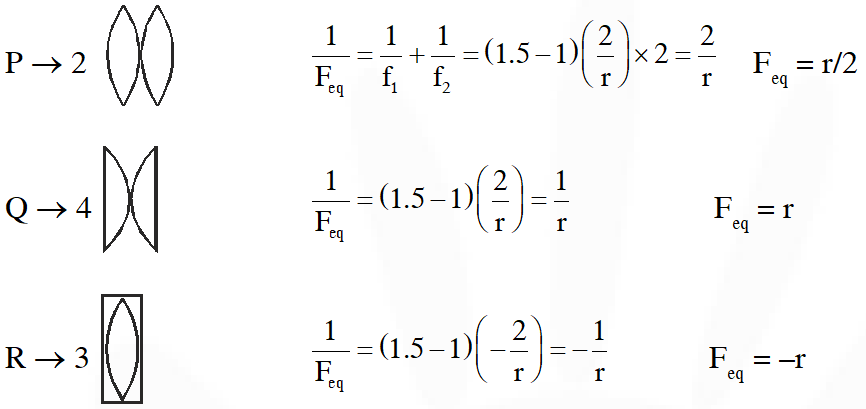
Q. Consider a concave mirror and a convex lens (refractive index = 1.5) of focal length 10 cm each, separated by a distance of 50 cm in air (refractive index = 1) as shown in the figure. An object is placed at a distance of 15 cm from the mirror. Its erect image formed by this combination has magnification $\mathrm{M}_{1}$. When the set-up is kept in a medium of refractive index 7/6 the magnification becomes $\mathrm{M}_{2}$. The magnitude $\left|\frac{M_{2}}{M_{1}}\right|$ is.
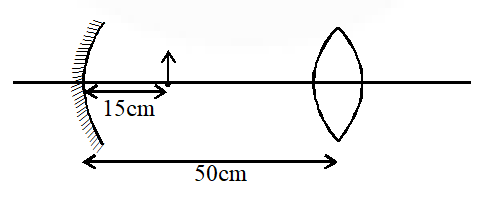 [JEE-Advance-2015]
[JEE-Advance-2015]
 [JEE-Advance-2015]
[JEE-Advance-2015]
Ans. 7
For reflectionfrom concave mirror,
$\frac{1}{\mathrm{v}}+\frac{1}{\mathrm{u}}=\frac{1}{\mathrm{f}} \Rightarrow \frac{1}{\mathrm{v}}-\frac{1}{15}=\frac{-1}{10}$
$\frac{1}{\mathrm{v}}=\frac{1}{15}-\frac{1}{10}=\frac{-1}{30}$
$\therefore \mathrm{v}=-30$
magnification $\left(\mathrm{m}_{1}\right)=-\frac{\mathrm{v}}{\mathrm{u}}=-2$
Now for refraction from lens,
$\frac{1}{\mathrm{v}}-\frac{1}{\mathrm{u}}=\frac{1}{\mathrm{f}} \Rightarrow \frac{1}{\mathrm{v}}=\frac{1}{10}-\frac{1}{20}=\frac{1}{20}$
$\therefore$ magnification $\left(\mathrm{m}_{2}\right)=\frac{\mathrm{v}}{\mathrm{u}}=-1$
$\therefore \mathrm{M}_{1}=\mathrm{m}_{1} \mathrm{m}_{2}=2$
Now when the set-up is immersed in liquid, no effect for the image formed by mirror.
we have $\left(\mu_{\mathrm{L}}-1\right)\left(\frac{1}{\mathrm{R}_{1}}-\frac{1}{\mathrm{R}_{2}}\right)=\frac{1}{10}$
$\Rightarrow\left(\frac{1}{\mathrm{R}_{1}}-\frac{1}{\mathrm{R}_{2}}\right)=\frac{1}{5}$
when lens is immersed in liquid,
$\frac{1}{\mathrm{f}_{\mathrm{lens}}}=\left(\frac{\mu_{\mathrm{L}}}{\mu_{\mathrm{S}}}-1\right)\left(\frac{1}{\mathrm{R}_{1}}-\frac{1}{\mathrm{R}_{2}}\right)=\frac{2}{7} \times \frac{1}{5}=\frac{2}{35}$
$\therefore \frac{1}{\mathrm{v}}-\frac{1}{\mathrm{u}}=\frac{1}{\mathrm{f}_{\mathrm{Liquid}}}$
$\Rightarrow \frac{1}{\mathrm{v}}=\frac{2}{35}-\frac{1}{20}=\frac{8-7}{140}=\frac{1}{140}$
$\therefore$ magnification $=-\frac{140}{20}=-7$
$\therefore \mathrm{M}_{2}=2 \times 7=14$
$\therefore\left|\frac{\mathrm{M}_{2}}{\mathrm{M}_{1}}\right|=7$
Q. Two identical glass rods $\mathrm{S}_{1}$ and $\mathrm{S}_{2}$ (refractive index = 1.5) have one convex end of radius of curvature 10 cm. They are placed with the curved surfaces at a distance d as shown in the figure, with their axes (shown by the dashded line) aligned. When a point source of light P is placed inside rod $\mathrm{S}_{1}$ on its axis at a distance of 50 cm from the curved face, the light rays emanating from it are found to be parallel to the axis inside $\mathrm{S}_{2}$. The distance d is :
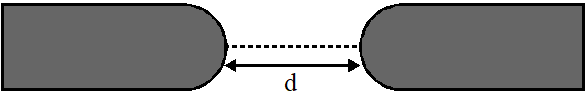 (A) 60 cm (B) 70 cm (C) 80 cm (D) 90 cm
[JEE-Advance-2015]
(A) 60 cm (B) 70 cm (C) 80 cm (D) 90 cm
[JEE-Advance-2015]
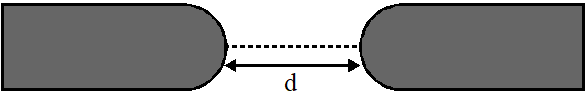 (A) 60 cm (B) 70 cm (C) 80 cm (D) 90 cm
[JEE-Advance-2015]
(A) 60 cm (B) 70 cm (C) 80 cm (D) 90 cm
[JEE-Advance-2015]
Ans. (B)
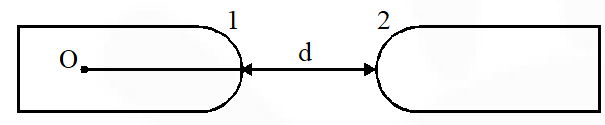
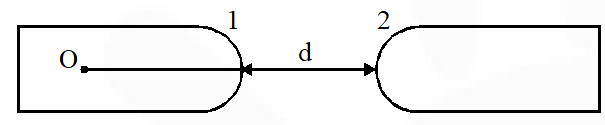 For first surface
$\frac{1}{V}-\frac{1.5}{-50}=\frac{1-1.5}{-10}$
V = 50 cm
for second surface
$\frac{1.5}{\infty}-\frac{1}{-(\mathrm{d}-50)}=\frac{1.5-1}{10}$
d = 70 cm
$\therefore(\mathrm{B})$
For first surface
$\frac{1}{V}-\frac{1.5}{-50}=\frac{1-1.5}{-10}$
V = 50 cm
for second surface
$\frac{1.5}{\infty}-\frac{1}{-(\mathrm{d}-50)}=\frac{1.5-1}{10}$
d = 70 cm
$\therefore(\mathrm{B})$
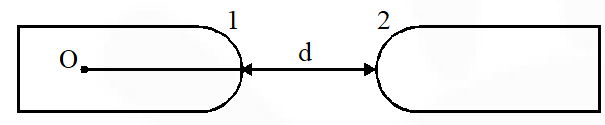
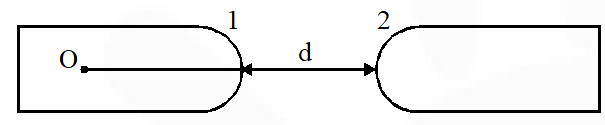 For first surface
$\frac{1}{V}-\frac{1.5}{-50}=\frac{1-1.5}{-10}$
V = 50 cm
for second surface
$\frac{1.5}{\infty}-\frac{1}{-(\mathrm{d}-50)}=\frac{1.5-1}{10}$
d = 70 cm
$\therefore(\mathrm{B})$
For first surface
$\frac{1}{V}-\frac{1.5}{-50}=\frac{1-1.5}{-10}$
V = 50 cm
for second surface
$\frac{1.5}{\infty}-\frac{1}{-(\mathrm{d}-50)}=\frac{1.5-1}{10}$
d = 70 cm
$\therefore(\mathrm{B})$
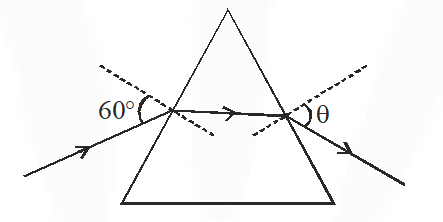
Q. A monochromatic beam of light is incident at $60^{\circ}$ on one face of an equilateral prism of refractive index n and emerges from the opposite face making an angle $\theta$(n) with the normal (see the figure). For n = $\sqrt{3}$ the value of $\theta$ is $60^{\circ}$ and $\frac{\mathrm{d} \theta}{\mathrm{dn}}=\mathrm{m}$. The value of m is.
 [JEE-Advance-2015]
[JEE-Advance-2015]
 [JEE-Advance-2015]
[JEE-Advance-2015]
Ans. 2
By snell's law
$1 \sin 60=n \sin r_{1} \Rightarrow \sin r_{1}=\frac{1}{2} r_{1}=30^{\circ} \quad \ldots \ldots(i)$
By differentiating 'w.r.t' n
$\mathrm{O}=\sin \mathrm{r}_{1}+\mathrm{n} \cos \mathrm{r}_{1}\left(\frac{\mathrm{dr}_{1}}{\mathrm{dn}}\right)$
$=\frac{1}{2}+\sqrt{3}(\sqrt{\frac{3}{2}}) \frac{\mathrm{dr}_{1}}{\mathrm{dn}}$
$\frac{\mathrm{d} \mathrm{r}_{1}}{\mathrm{dn}}=\frac{1}{3}$ ....(ii)
By applying snell's law
$n \sin r_{2}=1 \sin \theta$
$n \sin \left(60-r_{1}\right)=1 \sin \theta\left[\therefore A=r_{1}+r_{2}\right]$
By diffrentiating 'w.r.t' n
$\sin \left(60-r_{1}\right)-n \cos \left(60-r_{1}\right) \frac{d r_{1}}{d n}=\cos \theta \frac{d \theta}{d n}$$\sin \left(60-r_{1}\right)-n \cos \left(60-r_{1}\right) \frac{d r_{1}}{d n}=\cos \theta \frac{d \theta}{d n}$
By substituting value of $\mathrm{r}_{1}^{\prime}$ and $\frac{\mathrm{dr}_{1}}{\mathrm{dn}}$ from ( 1) and ( 2)
$\frac{\mathrm{d} \theta}{\mathrm{dn}}=2$

Q. For two structures namely $\mathrm{S}_{1}$ with $\mathrm{n}_{1}=\sqrt{45} / 4$ and $\mathrm{n}_{2}=3 / 2,$ and $\mathrm{S}_{2}$ with $\mathrm{n}_{1}=8 / 5$ and $\mathrm{n}_{2}=7 / 5$ and
taking the refractive index of water to be $4 / 3$ and that of air to be $1,$ the correct option(s) is (are)
(A) NA of $\mathrm{S}_{1}$ immersed in water is the same as that of $\mathrm{S}_{2}$ immersed in liquid of refractive index $\frac{16}{3 \sqrt{15}}$
(B) NA of $\mathrm{S}_{1}$ immersed in liquid of refractive index $\frac{6}{\sqrt{15}}$ is the same as that of $\mathrm{S}_{2}$ immersed in water.
(C) NA of $\mathrm{S}_{1}$ placed in air is the same as that of $\mathrm{S}_{2}$ immersed in liquid of refractive index .
(D) NA of $\mathrm{S}_{1}$ placed in air is the same as that of $\mathrm{S}_{2}$ placed in water.
[JEE-Advance-2015]
Ans. (A,C)
Let the whole structure is placed in a medium of refractive index n', then
$n^{\prime} \sin i=n_{1} \sin (90-\theta)$
$\mathrm{n}^{\prime} \sin \mathrm{i}=\mathrm{n}_{1} \cos \theta \quad \ldots(\mathrm{i})$
Here for $\mathrm{i}_{\mathrm{m}} ; \quad \theta=\mathrm{C}$ and $\sin \mathrm{C}=\frac{\mathrm{n}_{2}}{\mathrm{n}_{1}}$
from eq. (i), $\mathrm{n}^{\prime} \sin \mathrm{i}_{\mathrm{m}}=\mathrm{n}_{1} \sqrt{\frac{1-\mathrm{n}_{2}^{2}}{\mathrm{n}_{1}^{2}}}=\sqrt{\mathrm{n}_{1}^{2}-\mathrm{n}_{2}^{2}}$
$\Rightarrow \sin i_{m}=\frac{\sqrt{n_{1}^{2}-n_{2}^{2}}}{n^{\prime}}$
Now, for $(\mathrm{A})(\mathrm{NA})_{\mathrm{s} 1}=\frac{3}{4} \sqrt{\frac{45}{16}-\frac{9}{4}}=\frac{3}{4} \times \frac{3}{4}=\frac{9}{16}$
$(\mathrm{NA})_{\mathrm{s} 2}=\frac{3 \sqrt{15}}{16} \sqrt{\frac{64}{25}-\frac{49}{25}}=\frac{3 \sqrt{15}}{16} \frac{1}{5} \sqrt{15}=\frac{9}{16}$
For (B) $\quad(\mathrm{NA})_{\mathrm{s} 1}=\frac{\sqrt{15}}{6} \times \frac{3}{4}=\frac{\sqrt{15}}{8}$
$(\mathrm{NA})_{\mathrm{s} 2}=\frac{3}{4}=\frac{\sqrt{15}}{5}$ Not equal
For $(\mathrm{C})(\mathrm{NA})_{\mathrm{s} 1}=1 \times \frac{3}{4}=\frac{3}{4}$
$(\mathrm{NA})_{\mathrm{s} 2}=\frac{\sqrt{15}}{4} \times \frac{\sqrt{15}}{5}=\frac{15}{4 \times 5}=\frac{3}{4}$
For (D) $(\mathrm{NA})_{\mathrm{s} 1}=\frac{3}{4}$
$(\mathrm{NA})_{\mathrm{s} 2}=\frac{3}{4} \frac{\sqrt{15}}{5}$ Not equal
Q. If two structures of same cross-sectional area, but different numerical apertures $\mathrm{NA}_{1}$ and $\mathrm{NA}_{2}$ $\left(\mathrm{NA}_{2}<\mathrm{NA}_{1}\right)$ are joined longitudinally, the numerical aperture of the combined structure is
(A) $\frac{\mathrm{NA}_{1} \mathrm{NA}_{2}}{\mathrm{NA}_{1}+\mathrm{NA}_{2}}$
$(\mathrm{B}) \mathrm{NA}_{1}+\mathrm{NA}_{2}$
$(\mathrm{C}) \mathrm{NA}_{1}$
$(\mathrm{D}) \mathrm{NA}_{2}$
[JEE-Advance-2015]
Ans. (D)
$\begin{array}{ll}{\text { It is given that }} & {\mathrm{NA}_{2}<\mathrm{NA}_{1}} \\ {\Rightarrow \mathrm{i}_{\mathrm{m} 2}<\mathrm{i}_{\mathrm{m} 1}}\end{array}$
Hence if the combination can be placed both ways i.e. 1st structure & then 2nd structure and then reversed also, then the condition of TIR is satisfied for lower $\dot{\mathbf{1}}_{\mathrm{m}}$ then it can be satisfied for all other less angler as well.
Hence $\mathrm{NA}_{2}$ will be the numerical aperture of the combined structure.
Q. A parallel beam of light is incident from air at an angle on the side PQ of a right angled triangular prism of refractive index $\mathrm{n}=\sqrt{2}$. Light undergoes total internal reflection in the prism at the face PR when has a minimum value of $45^{\circ}$. The angle $\theta$ of the prism is :
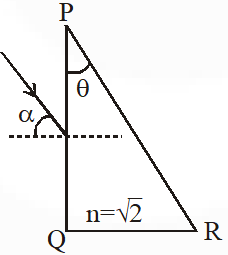 (A) $15^{\circ}$
(B) $22.5^{\circ}$
(C) $30^{\circ}$b
(D) $45^{\circ}$
[JEE-Advance-2016]
(A) $15^{\circ}$
(B) $22.5^{\circ}$
(C) $30^{\circ}$b
(D) $45^{\circ}$
[JEE-Advance-2016]
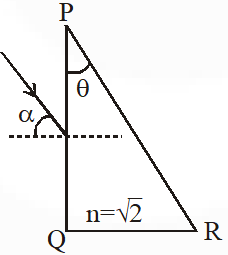 (A) $15^{\circ}$
(B) $22.5^{\circ}$
(C) $30^{\circ}$b
(D) $45^{\circ}$
[JEE-Advance-2016]
(A) $15^{\circ}$
(B) $22.5^{\circ}$
(C) $30^{\circ}$b
(D) $45^{\circ}$
[JEE-Advance-2016]
Ans. (A)
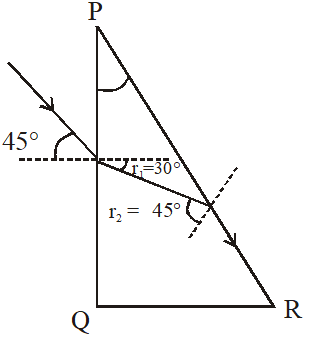 $1 \sin 45^{\circ}=\sqrt{2} \sin \mathrm{r}_{1}$
$\mathrm{r}_{2}-\mathrm{r}_{1}=\theta$
$\theta=45^{\circ}-30^{\circ}$
$\Rightarrow \theta=15^{\circ}$
$1 \sin 45^{\circ}=\sqrt{2} \sin \mathrm{r}_{1}$
$\mathrm{r}_{2}-\mathrm{r}_{1}=\theta$
$\theta=45^{\circ}-30^{\circ}$
$\Rightarrow \theta=15^{\circ}$
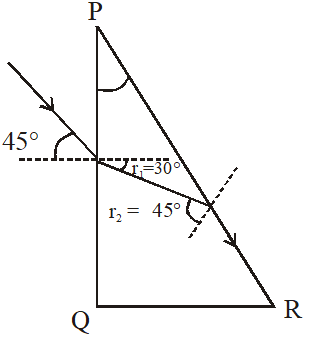 $1 \sin 45^{\circ}=\sqrt{2} \sin \mathrm{r}_{1}$
$\mathrm{r}_{2}-\mathrm{r}_{1}=\theta$
$\theta=45^{\circ}-30^{\circ}$
$\Rightarrow \theta=15^{\circ}$
$1 \sin 45^{\circ}=\sqrt{2} \sin \mathrm{r}_{1}$
$\mathrm{r}_{2}-\mathrm{r}_{1}=\theta$
$\theta=45^{\circ}-30^{\circ}$
$\Rightarrow \theta=15^{\circ}$
Q. A transparent slab of thickness d has a refractive index n(z) that increases with z. Here z is the vertical distance inside the slab, measured from the top. The slab is placed between two media with uniform refractive indices $\mathrm{n}_{1}$ and $\mathrm{n}_{2}\left(>\mathrm{n}_{1}\right)$, as shown in the figure. A ray of light is incident with angle $\theta_{\mathrm{i}}$ from medium 1 and emerges in medium 2 with refraction angle $\theta_{\mathrm{f}}$ with a lateral displacement . Which of the following statement(s) is(are) true ?
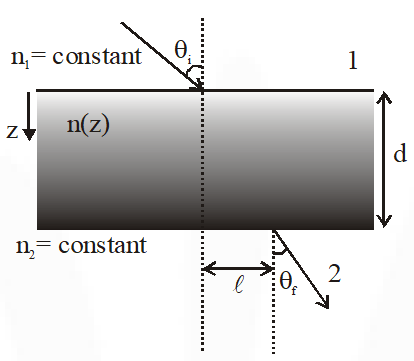 (A) $\ell$ is independent of $\mathrm{n}_{2}$
(B) $\ell$ is dependent on $\mathrm{n}(\mathrm{z})$
(C) $\mathrm{n}_{1} \sin \theta_{\mathrm{i}}=\left(\mathrm{n}_{2}-\mathrm{n}_{1}\right) \sin \theta_{\mathrm{f}}$
(D) $\mathrm{n}_{1} \sin \theta_{\mathrm{i}}=\mathrm{n}_{2} \sin \theta_{\mathrm{f}}$
[JEE-Advance-2016]
(A) $\ell$ is independent of $\mathrm{n}_{2}$
(B) $\ell$ is dependent on $\mathrm{n}(\mathrm{z})$
(C) $\mathrm{n}_{1} \sin \theta_{\mathrm{i}}=\left(\mathrm{n}_{2}-\mathrm{n}_{1}\right) \sin \theta_{\mathrm{f}}$
(D) $\mathrm{n}_{1} \sin \theta_{\mathrm{i}}=\mathrm{n}_{2} \sin \theta_{\mathrm{f}}$
[JEE-Advance-2016]
 (A) $\ell$ is independent of $\mathrm{n}_{2}$
(B) $\ell$ is dependent on $\mathrm{n}(\mathrm{z})$
(C) $\mathrm{n}_{1} \sin \theta_{\mathrm{i}}=\left(\mathrm{n}_{2}-\mathrm{n}_{1}\right) \sin \theta_{\mathrm{f}}$
(D) $\mathrm{n}_{1} \sin \theta_{\mathrm{i}}=\mathrm{n}_{2} \sin \theta_{\mathrm{f}}$
[JEE-Advance-2016]
(A) $\ell$ is independent of $\mathrm{n}_{2}$
(B) $\ell$ is dependent on $\mathrm{n}(\mathrm{z})$
(C) $\mathrm{n}_{1} \sin \theta_{\mathrm{i}}=\left(\mathrm{n}_{2}-\mathrm{n}_{1}\right) \sin \theta_{\mathrm{f}}$
(D) $\mathrm{n}_{1} \sin \theta_{\mathrm{i}}=\mathrm{n}_{2} \sin \theta_{\mathrm{f}}$
[JEE-Advance-2016]
Ans. (A,B,D)
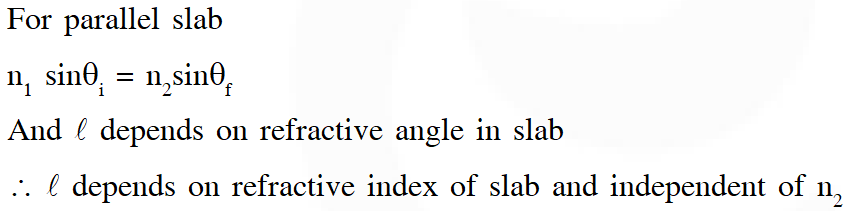
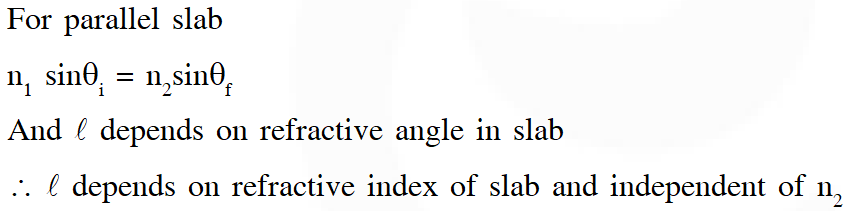
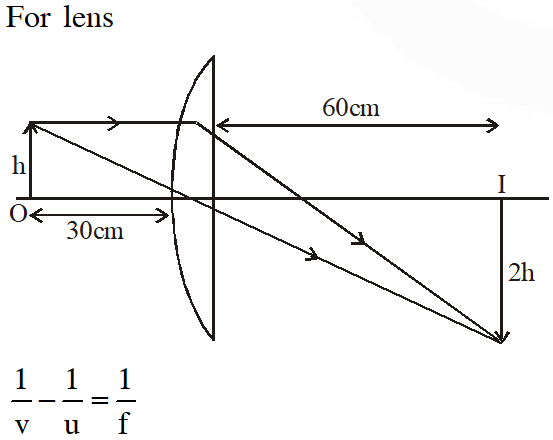
Q. A plano-convex lens is made of a material of refractive index n. When a small object is placed 30 cm away in front of the curved surface of the lens, an image of double the size of the object is produced. Due to reflection from the convex surface of the lens, another faint image is observed at a distance of 10 cm away from the lens. Which of the following statement(s) is(are) true?
(A) The refractive index of the lens is 2.5
(B) The radius of curvature of the convex surface is 45 cm
(C) The faint image is erect and real
(D) The focal length of the lens is 20 cm.
[JEE-Advance-2016]
Ans. (A,D)
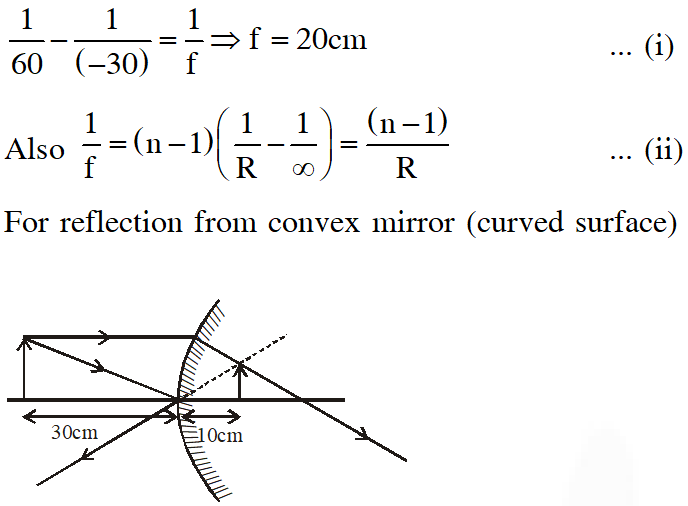
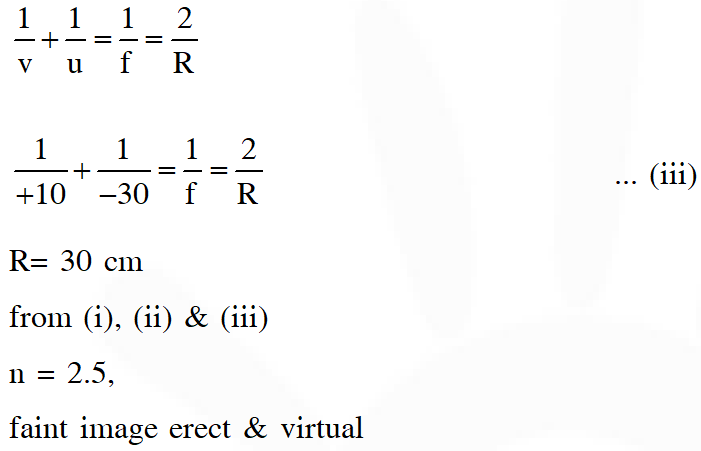

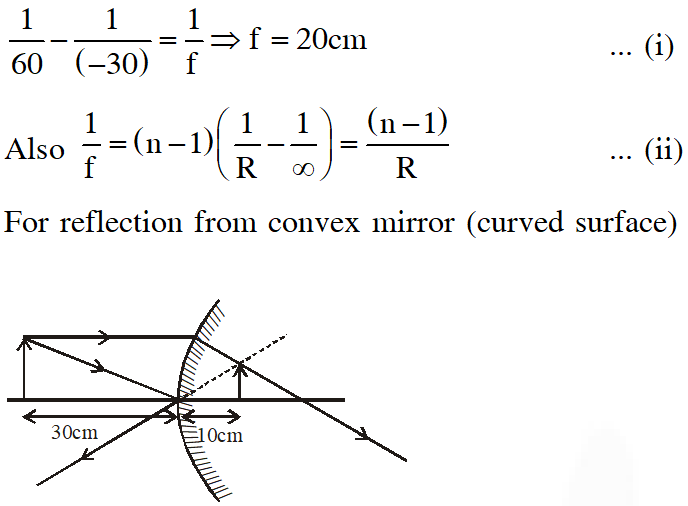
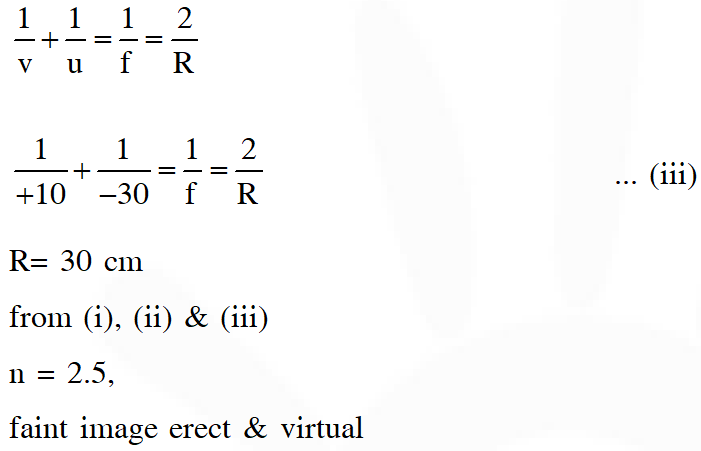
Q. A small object is placed 50 cm to the left of thin convex lens of focal length 30 cm. A convex spherical mirror of radius of curvature 100 cm is placed to the right of the lens at a distance of 50 cm. The mirror is tilted such that the axis of the mirror is at an angle = $30^{\circ}$ to the axis of the lens, as shown in the figure. If the origin of the coordinate system is taken to be at the centre of the lens, the coordinates (in cm) of the point (x, y) at which the image is formed are :
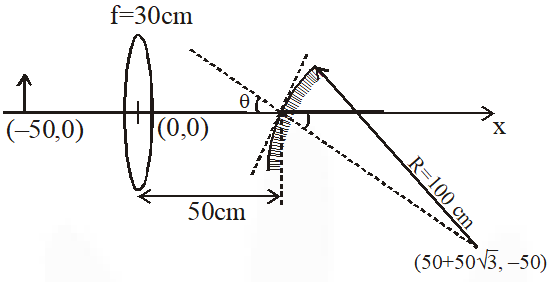 (A) $(25,25 \sqrt{3})$
$(\mathrm{B})\left(\frac{125}{3}, \frac{25}{\sqrt{3}}\right)$
(C) $(50-25 \sqrt{3}, 25)$
(D) (0, 0)
[JEE-Advance-2016]
(A) $(25,25 \sqrt{3})$
$(\mathrm{B})\left(\frac{125}{3}, \frac{25}{\sqrt{3}}\right)$
(C) $(50-25 \sqrt{3}, 25)$
(D) (0, 0)
[JEE-Advance-2016]
 (A) $(25,25 \sqrt{3})$
$(\mathrm{B})\left(\frac{125}{3}, \frac{25}{\sqrt{3}}\right)$
(C) $(50-25 \sqrt{3}, 25)$
(D) (0, 0)
[JEE-Advance-2016]
(A) $(25,25 \sqrt{3})$
$(\mathrm{B})\left(\frac{125}{3}, \frac{25}{\sqrt{3}}\right)$
(C) $(50-25 \sqrt{3}, 25)$
(D) (0, 0)
[JEE-Advance-2016]
Ans. (A)
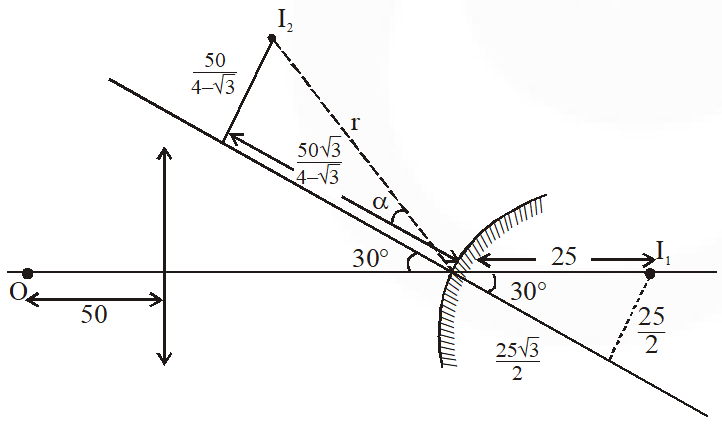 For lens $\mathrm{V}=\frac{(-50)(30)}{-50+30}=75$
For mirror $\mathrm{V}=\frac{\left(\frac{25 \sqrt{3}}{2}\right)(50)}{\frac{25 \sqrt{3}}{2}-50}=\frac{-50 \sqrt{3}}{4-\sqrt{3}}$
$\mathrm{m}=-\frac{\mathrm{v}}{\mathrm{u}}=\frac{\mathrm{h}_{2}}{\mathrm{h}_{1}} \Rightarrow \mathrm{h}_{2}=-\left(\frac{\frac{-50 \sqrt{3}}{4-\sqrt{3}}}{\frac{25 \sqrt{3}}{2}}\right) \cdot \frac{25}{2}$
$\mathrm{h}_{2}=\frac{+50}{4-\sqrt{3}}$
The x coordinate of the images $=50-v \cos 30+h_{2} \cos 60 \approx 25$
The y coordinate of the images $=v \sin 30+h_{2} \sin 60 \approx 25 \sqrt{3}$
For lens $\mathrm{V}=\frac{(-50)(30)}{-50+30}=75$
For mirror $\mathrm{V}=\frac{\left(\frac{25 \sqrt{3}}{2}\right)(50)}{\frac{25 \sqrt{3}}{2}-50}=\frac{-50 \sqrt{3}}{4-\sqrt{3}}$
$\mathrm{m}=-\frac{\mathrm{v}}{\mathrm{u}}=\frac{\mathrm{h}_{2}}{\mathrm{h}_{1}} \Rightarrow \mathrm{h}_{2}=-\left(\frac{\frac{-50 \sqrt{3}}{4-\sqrt{3}}}{\frac{25 \sqrt{3}}{2}}\right) \cdot \frac{25}{2}$
$\mathrm{h}_{2}=\frac{+50}{4-\sqrt{3}}$
The x coordinate of the images $=50-v \cos 30+h_{2} \cos 60 \approx 25$
The y coordinate of the images $=v \sin 30+h_{2} \sin 60 \approx 25 \sqrt{3}$
 For lens $\mathrm{V}=\frac{(-50)(30)}{-50+30}=75$
For mirror $\mathrm{V}=\frac{\left(\frac{25 \sqrt{3}}{2}\right)(50)}{\frac{25 \sqrt{3}}{2}-50}=\frac{-50 \sqrt{3}}{4-\sqrt{3}}$
$\mathrm{m}=-\frac{\mathrm{v}}{\mathrm{u}}=\frac{\mathrm{h}_{2}}{\mathrm{h}_{1}} \Rightarrow \mathrm{h}_{2}=-\left(\frac{\frac{-50 \sqrt{3}}{4-\sqrt{3}}}{\frac{25 \sqrt{3}}{2}}\right) \cdot \frac{25}{2}$
$\mathrm{h}_{2}=\frac{+50}{4-\sqrt{3}}$
The x coordinate of the images $=50-v \cos 30+h_{2} \cos 60 \approx 25$
The y coordinate of the images $=v \sin 30+h_{2} \sin 60 \approx 25 \sqrt{3}$
For lens $\mathrm{V}=\frac{(-50)(30)}{-50+30}=75$
For mirror $\mathrm{V}=\frac{\left(\frac{25 \sqrt{3}}{2}\right)(50)}{\frac{25 \sqrt{3}}{2}-50}=\frac{-50 \sqrt{3}}{4-\sqrt{3}}$
$\mathrm{m}=-\frac{\mathrm{v}}{\mathrm{u}}=\frac{\mathrm{h}_{2}}{\mathrm{h}_{1}} \Rightarrow \mathrm{h}_{2}=-\left(\frac{\frac{-50 \sqrt{3}}{4-\sqrt{3}}}{\frac{25 \sqrt{3}}{2}}\right) \cdot \frac{25}{2}$
$\mathrm{h}_{2}=\frac{+50}{4-\sqrt{3}}$
The x coordinate of the images $=50-v \cos 30+h_{2} \cos 60 \approx 25$
The y coordinate of the images $=v \sin 30+h_{2} \sin 60 \approx 25 \sqrt{3}$
Q. For an isosceles prism of angle A and refractive index µ, it is found that the angle of minimum deviation $\delta_{\mathrm{m}}$ = A. Which of the following options is/are correct ?
(A) At minimum deviation, the incident angle $\dot{\mathbf{1}}_{1}$ and the refracting angle $\mathrm{r}_{1}$ at the first refracting surface are related by $\mathbf{r}_{1}=\left(\mathbf{i}_{1} / 2\right)$
(B) For this prism, the refractive index µ and the angle of prism A are related as $\mathrm{A}=\frac{1}{2} \cos ^{-1}\left(\frac{\mu}{2}\right)$
(C) For this prism, the emergent ray at the second surface will be tangential to the surface when the angle of incidence at the first surface is $\mathrm{i}_{1}=\sin ^{-1}[\sin \mathrm{A} \sqrt{4 \cos ^{2} \frac{\mathrm{A}}{2}-1}-\cos \mathrm{A}]$
(D) For the angle of incidence $\mathbf{i}_{1}$ = A, the ray inside the prism is parallel to the base of the prism.
[JEE-Advance-2017]
Ans. (A,C,D)
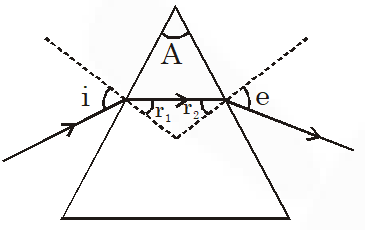 i = e (for minimum deviation)
$\mathrm{r}_{1}+\mathrm{r}_{2}=\mathrm{A}, \mathrm{r}_{1}=\mathrm{r}_{2}$
(A) $\delta_{\mathrm{m}}=2 \mathrm{i}-\mathrm{A}=\mathrm{A}$ (given)
$\Rightarrow \mathrm{i}=\mathrm{A}$
$\Rightarrow \mathrm{r}_{1}=\frac{\mathrm{A}}{2}=\frac{\mathrm{i}}{2}$
(B) $\mu=\frac{\sin (\mathrm{A})}{\sin (\mathrm{A} / 2)}=2 \cos \frac{\mathrm{A}}{2} \Rightarrow \mathrm{A}=2 \cos ^{-1}\left(\frac{\mu}{2}\right)$
(C) $\mu \sin \left(\mathrm{r}_{2}\right)=1$
$\sin \left(\mathrm{r}_{2}\right)=\frac{1}{\mu}$
$\mathrm{r}_{1}+\mathrm{r}_{2}=\mathrm{A}$
$\mathrm{r}_{1}=\mathrm{A}-\mathrm{r}_{2}$
$=\mathrm{A}-\sin ^{-1}\left[\frac{1}{\mu}\right]$
$\sin (\mathrm{i})=\mu \sin \left(\mathrm{r}_{1}\right)$
$\mathrm{i}=\sin ^{-1}\left[\mu \sin \left[\mathrm{A}-\sin ^{-1}\left[\frac{1}{\mu}\right]\right]\right.$
$\mathrm{i}_{\mathrm{g}}=\sin ^{-1}[\sqrt{\mu^{2}-1} \sin \mathrm{A}-\cos \mathrm{A}]=\sin ^{-1}\left[\mu \sin \left(\mathrm{A}-\theta_{\mathrm{C}}\right)\right]$
(Here $\left.\mu=2 \cos \frac{\mathrm{A}}{2}\right)$
(D) Condition of min. deviation $\mathrm{i}=\mathrm{e} \& \mathrm{r}_{1}=\mathrm{r}_{2}=\frac{\mathrm{A}}{2}$
Rays will be parallel to base.
i = e (for minimum deviation)
$\mathrm{r}_{1}+\mathrm{r}_{2}=\mathrm{A}, \mathrm{r}_{1}=\mathrm{r}_{2}$
(A) $\delta_{\mathrm{m}}=2 \mathrm{i}-\mathrm{A}=\mathrm{A}$ (given)
$\Rightarrow \mathrm{i}=\mathrm{A}$
$\Rightarrow \mathrm{r}_{1}=\frac{\mathrm{A}}{2}=\frac{\mathrm{i}}{2}$
(B) $\mu=\frac{\sin (\mathrm{A})}{\sin (\mathrm{A} / 2)}=2 \cos \frac{\mathrm{A}}{2} \Rightarrow \mathrm{A}=2 \cos ^{-1}\left(\frac{\mu}{2}\right)$
(C) $\mu \sin \left(\mathrm{r}_{2}\right)=1$
$\sin \left(\mathrm{r}_{2}\right)=\frac{1}{\mu}$
$\mathrm{r}_{1}+\mathrm{r}_{2}=\mathrm{A}$
$\mathrm{r}_{1}=\mathrm{A}-\mathrm{r}_{2}$
$=\mathrm{A}-\sin ^{-1}\left[\frac{1}{\mu}\right]$
$\sin (\mathrm{i})=\mu \sin \left(\mathrm{r}_{1}\right)$
$\mathrm{i}=\sin ^{-1}\left[\mu \sin \left[\mathrm{A}-\sin ^{-1}\left[\frac{1}{\mu}\right]\right]\right.$
$\mathrm{i}_{\mathrm{g}}=\sin ^{-1}[\sqrt{\mu^{2}-1} \sin \mathrm{A}-\cos \mathrm{A}]=\sin ^{-1}\left[\mu \sin \left(\mathrm{A}-\theta_{\mathrm{C}}\right)\right]$
(Here $\left.\mu=2 \cos \frac{\mathrm{A}}{2}\right)$
(D) Condition of min. deviation $\mathrm{i}=\mathrm{e} \& \mathrm{r}_{1}=\mathrm{r}_{2}=\frac{\mathrm{A}}{2}$
Rays will be parallel to base.
 i = e (for minimum deviation)
$\mathrm{r}_{1}+\mathrm{r}_{2}=\mathrm{A}, \mathrm{r}_{1}=\mathrm{r}_{2}$
(A) $\delta_{\mathrm{m}}=2 \mathrm{i}-\mathrm{A}=\mathrm{A}$ (given)
$\Rightarrow \mathrm{i}=\mathrm{A}$
$\Rightarrow \mathrm{r}_{1}=\frac{\mathrm{A}}{2}=\frac{\mathrm{i}}{2}$
(B) $\mu=\frac{\sin (\mathrm{A})}{\sin (\mathrm{A} / 2)}=2 \cos \frac{\mathrm{A}}{2} \Rightarrow \mathrm{A}=2 \cos ^{-1}\left(\frac{\mu}{2}\right)$
(C) $\mu \sin \left(\mathrm{r}_{2}\right)=1$
$\sin \left(\mathrm{r}_{2}\right)=\frac{1}{\mu}$
$\mathrm{r}_{1}+\mathrm{r}_{2}=\mathrm{A}$
$\mathrm{r}_{1}=\mathrm{A}-\mathrm{r}_{2}$
$=\mathrm{A}-\sin ^{-1}\left[\frac{1}{\mu}\right]$
$\sin (\mathrm{i})=\mu \sin \left(\mathrm{r}_{1}\right)$
$\mathrm{i}=\sin ^{-1}\left[\mu \sin \left[\mathrm{A}-\sin ^{-1}\left[\frac{1}{\mu}\right]\right]\right.$
$\mathrm{i}_{\mathrm{g}}=\sin ^{-1}[\sqrt{\mu^{2}-1} \sin \mathrm{A}-\cos \mathrm{A}]=\sin ^{-1}\left[\mu \sin \left(\mathrm{A}-\theta_{\mathrm{C}}\right)\right]$
(Here $\left.\mu=2 \cos \frac{\mathrm{A}}{2}\right)$
(D) Condition of min. deviation $\mathrm{i}=\mathrm{e} \& \mathrm{r}_{1}=\mathrm{r}_{2}=\frac{\mathrm{A}}{2}$
Rays will be parallel to base.
i = e (for minimum deviation)
$\mathrm{r}_{1}+\mathrm{r}_{2}=\mathrm{A}, \mathrm{r}_{1}=\mathrm{r}_{2}$
(A) $\delta_{\mathrm{m}}=2 \mathrm{i}-\mathrm{A}=\mathrm{A}$ (given)
$\Rightarrow \mathrm{i}=\mathrm{A}$
$\Rightarrow \mathrm{r}_{1}=\frac{\mathrm{A}}{2}=\frac{\mathrm{i}}{2}$
(B) $\mu=\frac{\sin (\mathrm{A})}{\sin (\mathrm{A} / 2)}=2 \cos \frac{\mathrm{A}}{2} \Rightarrow \mathrm{A}=2 \cos ^{-1}\left(\frac{\mu}{2}\right)$
(C) $\mu \sin \left(\mathrm{r}_{2}\right)=1$
$\sin \left(\mathrm{r}_{2}\right)=\frac{1}{\mu}$
$\mathrm{r}_{1}+\mathrm{r}_{2}=\mathrm{A}$
$\mathrm{r}_{1}=\mathrm{A}-\mathrm{r}_{2}$
$=\mathrm{A}-\sin ^{-1}\left[\frac{1}{\mu}\right]$
$\sin (\mathrm{i})=\mu \sin \left(\mathrm{r}_{1}\right)$
$\mathrm{i}=\sin ^{-1}\left[\mu \sin \left[\mathrm{A}-\sin ^{-1}\left[\frac{1}{\mu}\right]\right]\right.$
$\mathrm{i}_{\mathrm{g}}=\sin ^{-1}[\sqrt{\mu^{2}-1} \sin \mathrm{A}-\cos \mathrm{A}]=\sin ^{-1}\left[\mu \sin \left(\mathrm{A}-\theta_{\mathrm{C}}\right)\right]$
(Here $\left.\mu=2 \cos \frac{\mathrm{A}}{2}\right)$
(D) Condition of min. deviation $\mathrm{i}=\mathrm{e} \& \mathrm{r}_{1}=\mathrm{r}_{2}=\frac{\mathrm{A}}{2}$
Rays will be parallel to base.
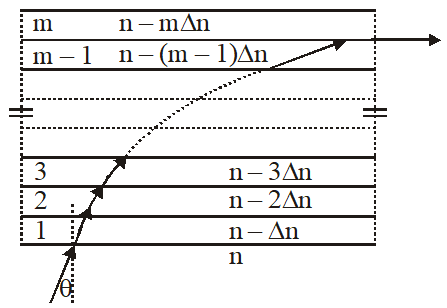
Q. A monochromatic light is travelling in a medium of refractive index n = 1.6. It enters a stack of glass layers from the bottom side at an angle $\theta=30^{\circ}$. The interfaces of the glass layers are parallel to each other. The refractive indices of different glass layers are monotonically decreasing as $\mathrm{n}_{\mathrm{m}}=\mathrm{n}-\mathrm{m} \Delta \mathrm{n}$, where $\mathrm{n}_{\mathrm{m}}$ is the refractive index of the mth slab and $\Delta \mathrm{n}=0.1$ (see the figure). The ray is refracted out parallel to the interface between the (m – 1)th and mth slabs from the right side of the stack. What is the value of m ?
 [JEE-Advance-2017]
[JEE-Advance-2017]
 [JEE-Advance-2017]
[JEE-Advance-2017]
Ans. 8
Applying snell's law between entry & exit surfaces,
n $\sin \theta=\mu \sin \left(\frac{\pi}{2}\right)$
Q. Sunlight of intensity $1.3 \mathrm{kW} \mathrm{m}^{-2}$ is incident normally on a thin convex lens of focal length 20 cm. Ignore the energy loss of light due to the lens and assume that the lens aperture size is much smaller than its focal length. The average intensity of light, in kW m–2, at a distance 22 cm from the lens on the other side is
[JEE-Advance-2018]
Ans. 130
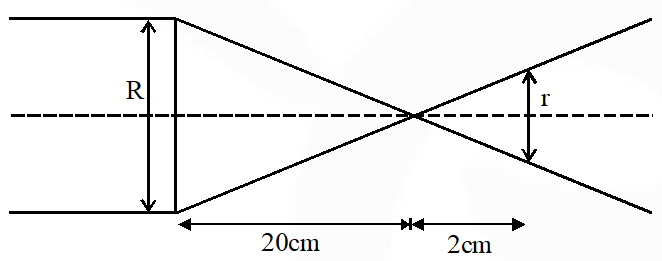 $\frac{\mathrm{r}}{\mathrm{R}}=\frac{2}{20}=\frac{1}{10}$
$\therefore$ Ratio of area $=\frac{1}{100}$
Let energy incident on lens be E.
$\therefore$ Given $\frac{\mathrm{E}}{\mathrm{A}}=1.3$
So final, $\frac{\mathrm{E}}{\mathrm{a}}=? ?$
E = A × 1.30
Also $\frac{\mathrm{a}}{\mathrm{A}}=\frac{1}{100}$
$\therefore$ Average intensity of light at $22 \mathrm{cm}=\frac{\mathrm{E}}{\mathrm{a}}=\frac{\mathrm{A} \times 1.3}{\mathrm{a}}=100 \times 1.3=130 \mathrm{kW} / \mathrm{m}^{2}$
$\frac{\mathrm{r}}{\mathrm{R}}=\frac{2}{20}=\frac{1}{10}$
$\therefore$ Ratio of area $=\frac{1}{100}$
Let energy incident on lens be E.
$\therefore$ Given $\frac{\mathrm{E}}{\mathrm{A}}=1.3$
So final, $\frac{\mathrm{E}}{\mathrm{a}}=? ?$
E = A × 1.30
Also $\frac{\mathrm{a}}{\mathrm{A}}=\frac{1}{100}$
$\therefore$ Average intensity of light at $22 \mathrm{cm}=\frac{\mathrm{E}}{\mathrm{a}}=\frac{\mathrm{A} \times 1.3}{\mathrm{a}}=100 \times 1.3=130 \mathrm{kW} / \mathrm{m}^{2}$
 $\frac{\mathrm{r}}{\mathrm{R}}=\frac{2}{20}=\frac{1}{10}$
$\therefore$ Ratio of area $=\frac{1}{100}$
Let energy incident on lens be E.
$\therefore$ Given $\frac{\mathrm{E}}{\mathrm{A}}=1.3$
So final, $\frac{\mathrm{E}}{\mathrm{a}}=? ?$
E = A × 1.30
Also $\frac{\mathrm{a}}{\mathrm{A}}=\frac{1}{100}$
$\therefore$ Average intensity of light at $22 \mathrm{cm}=\frac{\mathrm{E}}{\mathrm{a}}=\frac{\mathrm{A} \times 1.3}{\mathrm{a}}=100 \times 1.3=130 \mathrm{kW} / \mathrm{m}^{2}$
$\frac{\mathrm{r}}{\mathrm{R}}=\frac{2}{20}=\frac{1}{10}$
$\therefore$ Ratio of area $=\frac{1}{100}$
Let energy incident on lens be E.
$\therefore$ Given $\frac{\mathrm{E}}{\mathrm{A}}=1.3$
So final, $\frac{\mathrm{E}}{\mathrm{a}}=? ?$
E = A × 1.30
Also $\frac{\mathrm{a}}{\mathrm{A}}=\frac{1}{100}$
$\therefore$ Average intensity of light at $22 \mathrm{cm}=\frac{\mathrm{E}}{\mathrm{a}}=\frac{\mathrm{A} \times 1.3}{\mathrm{a}}=100 \times 1.3=130 \mathrm{kW} / \mathrm{m}^{2}$
Q. A wire is bent in the shape of a right angled triangle and is placed in front of a concave mirror of focal length f, as shown in the figure. Which of the figures shown in the four options qualitatively represent(s) the shape of the image of the bent wire ? (These figures are not to scale.) ?
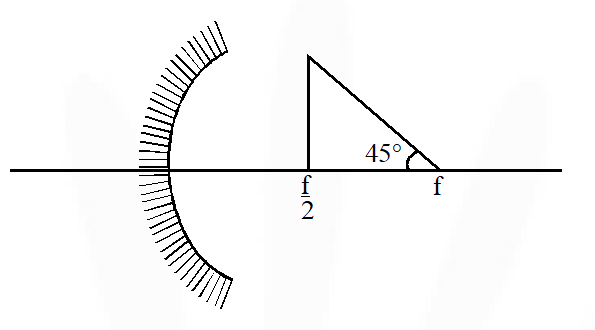
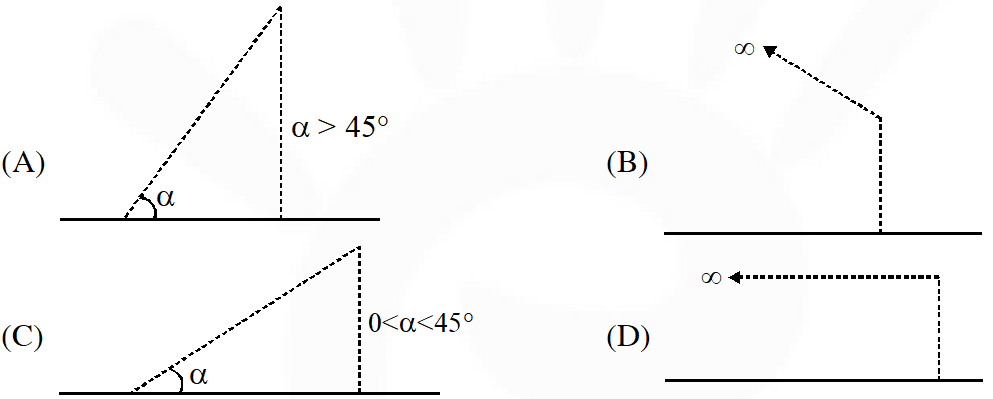 [JEE-Advance-2018]
[JEE-Advance-2018]
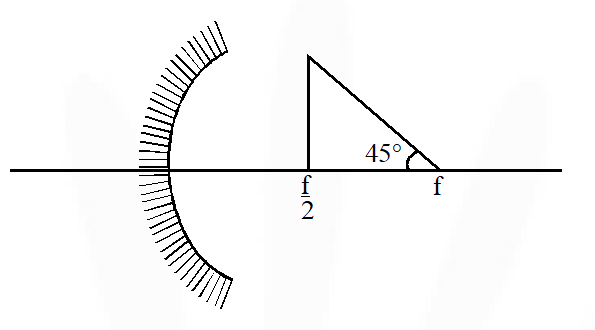
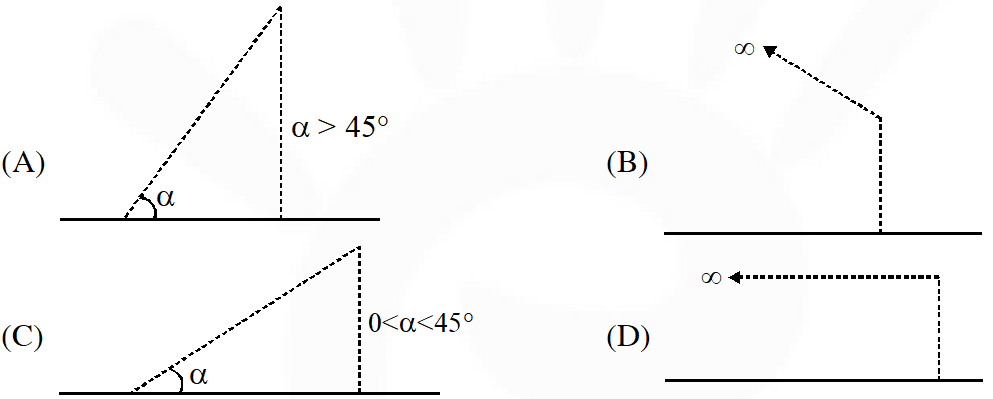 [JEE-Advance-2018]
[JEE-Advance-2018]
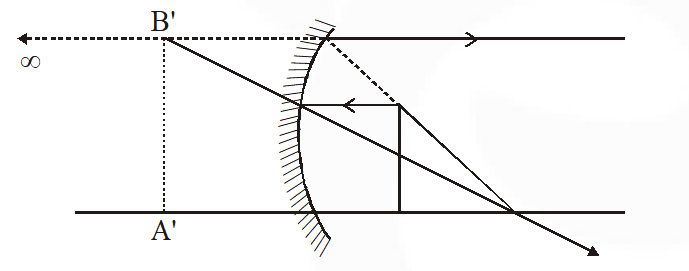
Ans. (D)
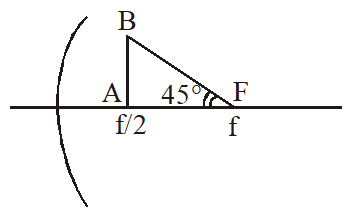 Distance of point A is f/2
Let A' is the image of A from mirror, for this image
$\frac{1}{\mathrm{v}}+\frac{1}{-\mathrm{f} / 2}=\frac{1}{-\mathrm{f}}$
$\frac{1}{\mathrm{v}}=\frac{2}{\mathrm{f}}-\frac{1}{\mathrm{f}}=\frac{1}{\mathrm{f}}$
image of line AB should be perpendicular to the principle axis & image of F will form at infinity, therefor correct image diagram is
Distance of point A is f/2
Let A' is the image of A from mirror, for this image
$\frac{1}{\mathrm{v}}+\frac{1}{-\mathrm{f} / 2}=\frac{1}{-\mathrm{f}}$
$\frac{1}{\mathrm{v}}=\frac{2}{\mathrm{f}}-\frac{1}{\mathrm{f}}=\frac{1}{\mathrm{f}}$
image of line AB should be perpendicular to the principle axis & image of F will form at infinity, therefor correct image diagram is
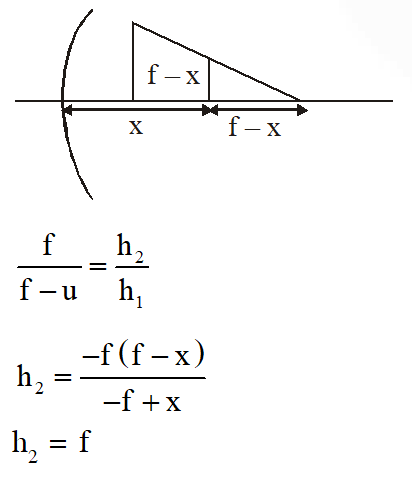
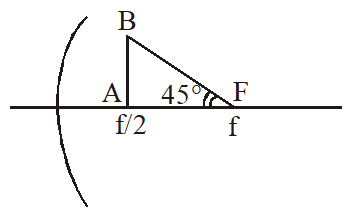 Distance of point A is f/2
Let A' is the image of A from mirror, for this image
$\frac{1}{\mathrm{v}}+\frac{1}{-\mathrm{f} / 2}=\frac{1}{-\mathrm{f}}$
$\frac{1}{\mathrm{v}}=\frac{2}{\mathrm{f}}-\frac{1}{\mathrm{f}}=\frac{1}{\mathrm{f}}$
image of line AB should be perpendicular to the principle axis & image of F will form at infinity, therefor correct image diagram is
Distance of point A is f/2
Let A' is the image of A from mirror, for this image
$\frac{1}{\mathrm{v}}+\frac{1}{-\mathrm{f} / 2}=\frac{1}{-\mathrm{f}}$
$\frac{1}{\mathrm{v}}=\frac{2}{\mathrm{f}}-\frac{1}{\mathrm{f}}=\frac{1}{\mathrm{f}}$
image of line AB should be perpendicular to the principle axis & image of F will form at infinity, therefor correct image diagram is