RD Sharma Solutions for Class 9 Maths Chapter 1 Number System - Free PDF Download

Hey, are you a class 9 student and looking for ways to download RD Sharma Solutions for Class 9 Maths Chapter 1 "Number System"? If yes. Then read this post till the end.

In this article, we have listed RD Sharma Solutions for Class 9 Maths Chapter 1 in PDF that is prepared by Kota’s top IITian’s Faculties by keeping Simplicity in mind.

If you want to learn and understand class 9 Maths Chapter 1 "Number System" in an easy way then you can use these solutions PDF.

Chapter 1 of RD Sharma Class 9 deals with Whole Numbers, Rational Numbers, Irrational Numbers, and  Natural Numbers. If you want to improve your basic fundamentals of Number systems then you can this.

RD Sharma Solutions helps students to Practice important concepts of subjects easily. RD Sharma class 9 solutions provide detailed explanations of all the  exercise questions that students can use to clear their doubts instantly.

If you want to become good at Math then it is very important for you to have a good knowledge of all the important topics of class 9 math, so to learn and practice those topics you can use eSaral RD Sharma Solutions.

In this article, we have listed RD Sharma Solutions for Class 9 Maths Chapter 1 that you can download to start your preparations anytime.

So, without wasting more time Let’s start.

RD Sharma Solutions for Class 9 Maths Chapter 1 Number System - Free PDF Download

Question 1: Express the following rational numbers as decimals:

(i) $\frac{42}{100}$

(ii) $\frac{327}{500}$

(iii) $\frac{15}{4}$

Solution. (i) Given rational number is $\frac{42}{100}$

Now we have to express this rational number into decimal form. So we will use long division method as below.



Hence,



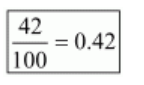
(ii) Given rational number is $\frac{327}{500}$

Now we have to express this rational number into decimal form. So we will use long division method as below.



Hence,



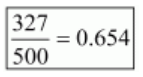
(iii) Given rational number is $\frac{15}{4}$

Now we have to express this rational number into decimal form. So we will use long division method as below.



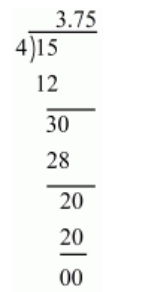
Hence, $\frac{15}{4}=3.75$

Question 2: Express the following rational numbers as decimals:

(i) $\frac{2}{3}$

(ii) $-\frac{4}{9}$

(iii) $\frac{-2}{15}$

(iv) $-\frac{22}{13}$

(v) $\frac{437}{999}$

(vi) $\frac{33}{26}$

Solution. (i) Given rational number is $\frac{2}{3}$

Now we have to express this rational number into decimal form. So we will use long division method



Therefore $\frac{2}{3}=0.6666$

$\Rightarrow \frac{2}{3}=0 . \overline{6}$

Hence,



(ii) Given rational number is $-\frac{4}{9}$


Now we have to express this rational number into decimal form. So we will use long division method



Therefore, $\frac{4}{9}=0.444$

$\Rightarrow-\frac{4}{9}=-0 . \overline{4}$

Hence,



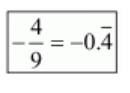
(iii) Given rational number is $-\frac{2}{15}$

Now we have to express this rational number into decimal form. So we will use long division method



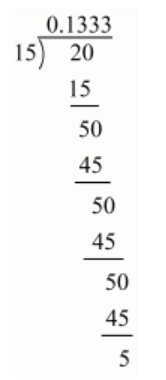
Therefore $\frac{2}{15}=0.1333$

$\Rightarrow \frac{2}{15}=0.1 \overline{3}$

Hence,



(iv) Given rational number is $-\frac{22}{13}$

Now we have to express this rational number into decimal form. So we will use long division method



Therefore $\frac{22}{13}=1.692307 \ldots$

$\Rightarrow \frac{22}{13}=1 . \overline{692307}$

Hence,



(v) Given rational number is $\frac{437}{999}$

Now we have to express this rational number into decimal form. So we will use long division method



$\Rightarrow \frac{437}{999}=0 . \overline{437}$

Hence,



(vi) Given rational number is $\frac{33}{26}$

Now we have to express this rational number into decimal form. So we will use long division method



Therefore $\frac{33}{26}=1.2 \overline{692307} \ldots$

Hence,



Question $3:$Look at several examples of rational numbers in the form $\frac{p}{q}(q \neq 0)$, where $p$ and $q$ are integers with no common factors other than 1 and having terminating decimal representations. Can you guess what property $q$ must satisfy?

Solution. Prime factorization is the process of finding which prime numbers you need to multiply together to get a certain number. So prime factorization of denominators $(q)$ must have only the power of 2 or 5 or both.

Question 1:Express each of the following decimals in the form $\frac{p}{q}$ :

(i) $0.39$

(ii) $0.750$

(iii) $2.15$

(iv) $7.010$ (iv) $7.010$

(v) $9.90$

(vi) $1.0001$

Solution. (i) Given decimal is $0.39$

Now we have to convert given decimal number into the $\frac{p}{q}$ form

Let $\frac{p}{q}=0.39$

$\Rightarrow \frac{p}{q}=\frac{39}{100}$

Hence,



(ii) Given decimal is $0.750$

Now we have to convert given decimal number into $\frac{p}{q}$ form

Let $\frac{p}{q}=0.750$

$\Rightarrow \frac{p}{q}=\frac{750}{1000}$

$\Rightarrow \frac{p}{q}=\frac{75}{100}$

$\Rightarrow \frac{p}{q}=\frac{3}{4}$

Hence,



(iii) Given decimal is $2.15$

Now we have to express the given decimal number into $\frac{p}{q}$ form

Let $\frac{p}{q}=2.15$

$\Rightarrow \frac{p}{q}=\frac{215}{100}$

$\Rightarrow \frac{p}{q}=\frac{43}{20}$

Hence,



(iv) Given decimal is $7.010$

Now we have to express the given decimal number into $\frac{p}{q}$ form

Let $\frac{p}{q}=7.010$

$\Rightarrow \frac{p}{q}=\frac{7010}{1000}$

$\Rightarrow \frac{p}{q}=\frac{701}{100}$

Hence,



(v) Given decimal is $9.90$

Now we have to find given decimal number into $\frac{p}{q}$ form

Let $\frac{p}{q}=9.90$

$\Rightarrow \frac{p}{q}=\frac{990}{100}$

$\Rightarrow \frac{p}{q}=\frac{99}{10}$

Hence, $9.90=\frac{99}{10}$

(vi) Given decimal is $1.0001$

Now we have to find given decimal number into $\frac{p}{q}$ for

$\frac{p}{q}=1.0001 \Rightarrow \frac{p}{q}=\frac{10001}{10000}$

Hence,



Question 2: Express each of the following decimals in the form $\frac{p}{q}$ :

(i) $0 . \overline{4}$

(ii) $0 . \overline{37}$

(iii) $0 . \overline{54}$

(iv) $0 . \overline{621}$

(v) $125 . \overline{3}$

(vi) $4 . \overline{7}$

(vii) $0 . \overline{47}$

Solution. (i) Let $x=0 . \overline{4}$

$\Rightarrow x=0.44444 \ldots$

$10 x=4.444 \ldots$

$\Rightarrow 10 x=4+x$

$\Rightarrow 9 x=4$

$\Rightarrow x=\frac{4}{9}$

Hence,



(ii) Let $x=0 . \overline{37}$

$\Rightarrow x=0.373737 \ldots$

$\Rightarrow 100 x=37.3737 \ldots$

$\Rightarrow 100 x=37+0.3737 \ldots$

$\Rightarrow 100 x=37+x$

$\Rightarrow 99 x=37$

$\Rightarrow x=\frac{37}{99}$

Hence,



(iii) Let $x=0 . \overline{54}$

$\Rightarrow x=0.545454 \ldots$

$\Rightarrow 100 x=54.5454 \ldots$

$\Rightarrow 100 x=54+0.5454 \ldots$

$\Rightarrow 100 x=54+x$

$\Rightarrow 99 x=54$

$\Rightarrow x=\frac{54}{99}=\frac{6}{11}$

Hence,



(iv) Let $x=0 . \overline{621}$

$\Rightarrow x=0.621621621 \ldots$

$\Rightarrow 1000 x=621.621621 \ldots$

$\Rightarrow 1000 x=621+0.621621 \ldots$

$\Rightarrow 1000 x=621+x$

$\Rightarrow 999 x=621$

$\Rightarrow x=\frac{621}{999}=\frac{207}{333}$

$\Rightarrow x=\frac{23}{37}$

Hence,



(v) Let $x=125 \overline{.3}$

$\Rightarrow x=125+0 . \overline{3}$

$\Rightarrow x=125+\frac{1}{3}\left(\because 0 . \overline{3}=\frac{1}{3}\right)$

$\Rightarrow x=\frac{375+1}{3}$

$\Rightarrow x=\frac{376}{3}$

Hence,



(vi) Let $x=4 . \overline{7}$

$x=4+0 . \overline{7}$

Let $y=0 . \overline{7}=0.777 \ldots$

$\Rightarrow 10 y=7+0.777 \ldots$

$\Rightarrow 10 y=7+y$

$\Rightarrow y=\frac{7}{9}$

Therefore,

$x=4+\frac{7}{9}=\frac{43}{9}$

Hence,



(vii) Let $x=0.4 \overline{7}$

$\Rightarrow 10 x=4+0 . \overline{7}$

Since, $0 . \overline{7}=\frac{7}{9}$

Therefore,

$\Rightarrow 10 x=4+\frac{7}{9}=\frac{43}{9}$

$\Rightarrow x=\frac{43}{90}$

Hence,



Question 1: Define an irrational number.

Solution. An irrational number is a real number that cannot be reduced to any ratio between an integer $p$ and a natural number $q$.

If the decimal representation of an irrational number is non-terminating and non-repeating, then it is called irrational number. For example $\sqrt{3}=1.732 \ldots \ldots .$

Question 2: Explain, how irrational numbers differ from rational numbers?

Solution. Every rational number must have either terminating or non-terminating but irrational number must have non- terminating and non-repeating decimal representation.

A rational number is a number that can be written as simple fraction (ratio) and denominator is not equal to zero while an irrational is a number that cannot be written as a ratio.

Question 3: Examine, whether the following numbers are rational or irrational:

(i) $\sqrt{7}$

(ii) $\sqrt{4}$

(iii) $2+\sqrt{3}$

(iv) $\sqrt{3}+\sqrt{2}$

(v) $\sqrt{3}+\sqrt{5}$

(vi) $(\sqrt{2}-2)^{2}$

(viii) $(\sqrt{2}+\sqrt{3})^{2}$

(viii) $(\sqrt{2}+\sqrt{3})^{2}$

(ix) $\sqrt{5}-2$

(x) $\sqrt{23}$

(xi) $\sqrt{225}$

(xii) $0.3796$

(xiii) $7.478478$

(xiv) $1.101001000100001$

Solution. (i) Let $x=\sqrt{7}$

Therefore,

$$x=2.645751311064 \ldots$$

It is non-terminating and non-repeating

Hence $\sqrt{7}$ is an irrational number

(ii) Let $x=\sqrt{4}$

Therefore,

$x=2$

It is terminating.

Hence $\sqrt{4}$ is a rational number.

(iii) Let $x=2+\sqrt{3}$ be the rational

Squaring on both sides

$\Rightarrow x^{2}=(2+\sqrt{3})^{2}$

$\Rightarrow x^{2}=4+3+4 \sqrt{3}$

$\Rightarrow x^{2}=7+4 \sqrt{3}$

$\Rightarrow x^{2}-7=4 \sqrt{3}$

$\Rightarrow \frac{x^{2}-7}{4}=\sqrt{3}$

Since, $x$ is rational

$\Rightarrow x^{2}$ is rational

$\Rightarrow x^{2}-7$ is rational

$\Rightarrow \frac{x^{2}-7}{4}$ is rational

$\Rightarrow \sqrt{3}$ is rational

But, $\sqrt{3}$ is irrational

So, we arrive at a contradiction.

Hence $2+\sqrt{3}$ is an irrational number

(iv) Let $x=\sqrt{3}+\sqrt{2}$ be the rational number

Squaring on both sides, we get

$\Rightarrow x^{2}=(\sqrt{3}+\sqrt{2})^{2}$

$\Rightarrow x^{2}=3+2+2 \sqrt{6}$

$\Rightarrow x^{2}=5+2 \sqrt{6}$

$\Rightarrow x^{2}-5=2 \sqrt{6}$

$\Rightarrow \frac{x^{2}-5}{2}=\sqrt{6}$

Since, x is a rational number

$\Rightarrow x^{2}$ is rational number

$\Rightarrow x^{2}-5$ is rational number

$\Rightarrow \frac{x^{2}-5}{2}$ is rational number

$\Rightarrow \sqrt{6}$ is rational number

But $\sqrt{6}$ is an irrational number

So, we arrive at contradiction

Hence $\sqrt{3}+\sqrt{2}$ is an irrational number

(v) Let $x=\sqrt{3}+\sqrt{5}$ be the rational number

Squaring on both sides, we get

$\Rightarrow x^{2}=(\sqrt{3}+\sqrt{5})^{2}$

$\Rightarrow x^{2}=3+5+2 \sqrt{15}$

$\Rightarrow x^{2}=8+2 \sqrt{15}$

$\Rightarrow x^{2}-8=2 \sqrt{15}$

$\Rightarrow \frac{x^{2}-8}{2}=\sqrt{15}$

Now, x is rational number

$\Rightarrow x^{2}$ is rational number

$\Rightarrow x^{2}-8$ is rational number

$\Rightarrow \frac{x^{2}-8}{2}$ is rational number

$\Rightarrow \sqrt{15}$ is rational number

But $\sqrt{15}$ is an irrational number

So, we arrive at a contradiction

Hence $\sqrt{3}+\sqrt{5}$ is an irrational number

(vi) Let $x=(\sqrt{2}-2)^{2}$ be a rational number.

$x=(\sqrt{2}-2)^{2}$

$\Rightarrow x=2+4-4 \sqrt{2}$

$\Rightarrow x=6-4 \sqrt{2}$

$\Rightarrow \frac{x-6}{-4}=\sqrt{2}$

Since, x is rational number,

$\Rightarrow x-6$ is a rational $n u 8$ mber

$\Rightarrow \frac{x-6}{-4}$ is a rational number

$\Rightarrow \sqrt{2}$ is a rational number

But we know that $\sqrt{2}$ is an irrational number, which is a contradiction

So $(\sqrt{2}-\sqrt{2})^{2}$ is an irrational number

(vii) Let $x=(2-\sqrt{2})(2+\sqrt{2})$

$\Rightarrow x=(2)^{2}-(\sqrt{2})^{2} \quad\left\{\right.$ As $\left.(a+b)(a-b)=a^{2}-b^{2}\right\}$

$\Rightarrow x=4-2$

$\Rightarrow x=2$

So $(2-\sqrt{2})(2+\sqrt{2})$ is a rational number

(viii) Let $x=(\sqrt{2}+\sqrt{3})^{2}$ be rational number

Using the formula $(a+b)^{2}=a^{2}+b^{2}+2 a b$

$\Rightarrow x=(\sqrt{2})^{2}+(\sqrt{3})^{2}+2(\sqrt{2})(\sqrt{3})$

$\Rightarrow x=2+3+2 \sqrt{6}$

$\Rightarrow x=5+2 \sqrt{6}$

$\Rightarrow \frac{x-5}{2}=\sqrt{6}$

$\Rightarrow \frac{x-5}{2}$ is a rational number

$\Rightarrow \sqrt{6}$ is a rational number

But we know that $\sqrt{6}$ is an irrational number

So, we arrive at a contradiction

So $(\sqrt{2}+\sqrt{3})^{2}$ is an irrational number.

(ix) Let $x=\sqrt{5}-2$ be the rational number

Squaring on both sides, we get

$x=\sqrt{5}-2$

$x^{2}=(\sqrt{5}-2)^{2}$

$x^{2}=25+4-4 \sqrt{5}$

$x^{2}-29=-4 \sqrt{5}$

$\frac{x^{2}-29}{-4}=\sqrt{5}$

Now, x is rational

$x^{2}$ is rational.

So, $x^{2}-29$ is rational

$\frac{\mathrm{x}^{2}-29}{-4}=\sqrt{5}$ is rational.

But, $\sqrt{5}$ is irrational. So we arrive at contradiction

Hence $x=\sqrt{5}-2$ is an irrational number

$(\mathrm{x}) \mathrm{Let}$

$x=\sqrt{23}$

$x=4.79583 \ldots$

It is non-terminating or non-repeating

Hence $\sqrt{23}$ is an irrational number

(xi) Let $x=\sqrt{225}$

$\Rightarrow x=15$

(xii) Given $0.3796$.

It is terminating

Hence it is a rational number

(xiii) Given number $x=7.478478 \ldots$

$\Rightarrow x=7 . \overline{478}$

It is repeating

Hence it is a rational number

(xiv) Given number is $x=1.1010010001 \ldots$

It is non-terminating or non-repeating

Hence it is an irrational number

Question 4: Identify the following as rational or irrational numbers. Give the decimal representation of rational numbers:

(i) $(\sqrt{4})$

(ii) $3 \sqrt{18}$

(iii) $\sqrt{1.44}$

(iv) $\sqrt{\frac{9}{27}}$

(v) $-\sqrt{64}$

(vi) $\sqrt{100}$

Solution. (i) Given number is $x=\sqrt{4}$

$x=2$, which is a rational number

(ii) Given number is $3 \sqrt{18}$

$\Rightarrow 3 \sqrt{18}=3 \sqrt{3 \times 3 \times 2}$

$\Rightarrow 3 \sqrt{18}=3 \times 3 \sqrt{2}$

$\Rightarrow 3 \sqrt{18}=3 \times 3 \sqrt{2}$

$\Rightarrow 3 \sqrt{18}=18 \sqrt{2}$

$3 \sqrt{18}=3 \sqrt{3 \times 3 \times 2}=3 \times 3 \sqrt{2}=9 \sqrt{2}$

So it is an irrational number

(iii) Given number is $\sqrt{1.44}$

Now we have to check whether it is rational or irrational

$\Rightarrow \sqrt{1.44}=\sqrt{\frac{144}{100}}$

$\Rightarrow \sqrt{1.44}=\frac{\sqrt{144}}{\sqrt{100}}$

$\Rightarrow \sqrt{1.44}=\frac{12}{10}$

$\Rightarrow \sqrt{1.44}=\frac{6}{5}$

$\Rightarrow \sqrt{1.44}=1.2$

So it is a rational

(iv) Given that $\sqrt{\frac{9}{27}}$

Now we have to check whether it is rational or irrational

$\Rightarrow \sqrt{\frac{9}{27}}=\frac{\sqrt{9}}{\sqrt{27}}$

$\Rightarrow \sqrt{\frac{9}{27}}=\frac{3}{\sqrt{3 \times 3 \times 3}}$

$\Rightarrow \sqrt{\frac{9}{27}}=\frac{3}{3 \sqrt{3}}$

$\Rightarrow \sqrt{\frac{9}{27}}=\frac{1}{\sqrt{3}}$

So it is an irrational number

(v) Given that $-\sqrt{64}$

Now we have to check whether it is rational or irrational

Since, $-\sqrt{64}=-8$

So it is a rational number (vi) Given that $\sqrt{100}$

Now we have to check whether it is rational or irrational

Since, $\sqrt{100}=10$

So it is rational number

Question 5: In the following equations, find which variables $x, y, z$ etc. represent rational or irrational numbers:

(i) $x^{2}=5$

(ii) $y^{2}=9$

(iii) $z^{2}=0.04$

$(\mathrm{iv}) u^{2}=\frac{17}{4}$

(v) $v^{2}=3$

(vi) $w^{2}=27$

(vii) $t^{2}=0.4$

Solution. (i) Given that $x^{2}=5$

Now we have to find the value of $x$

Since $x^{2}=5$

$\Rightarrow x=\sqrt{5}$

So it x is an irrational number

(ii) Given that $y^{2}=9$

Now we have to find the value of y

$y^{2}=9$

$\Rightarrow y=\sqrt{9}$

$\Rightarrow y=3$

So y is a rational number

(iii) Given that $z^{2}=0.04$

Now we have to find the value of z

$\Rightarrow z^{2}=\frac{4}{100}$

$\Rightarrow z=\sqrt{\frac{4}{100}}$

$\Rightarrow z=\frac{2}{10}$

$\Rightarrow z=\frac{1}{5}$

So it is rational number

(iv) Given that $u^{2}=\frac{17}{4}$

Now we have to find the value of u

$u^{2}=\frac{17}{4}$

$\Rightarrow u=\sqrt{\frac{17}{4}}$

$\Rightarrow u=\frac{\sqrt{17}}{2}$

So it is an irrational number

(v) Given that $v^{2}=3$

Now we have to find the value of v

$v^{2}=3$

$\Rightarrow v=\sqrt{3}$

So it is an irrational number

(vi) Given that $w^{2}=27$

Now we have to find the value of w

$\Rightarrow w=\sqrt{27}$

$\Rightarrow w=\sqrt{3 \times 3 \times 3}$

$\Rightarrow w=3 \sqrt{3}$

So it is an irrational number

(vii) Given that $t^{2}=0.4$

Now we have to find the value of t

$\Rightarrow t=\sqrt{0.4}$

$\Rightarrow t=\sqrt{\frac{4}{10}}$

$\Rightarrow t=\frac{2}{\sqrt{10}}$

So it is an irrational number

Question $6:$ Give two rational numbers lying between $0.232332333233332 \ldots$ and $0.212112111211112 .$

Solution. Let

$a=0.232332333233332 \ldots$

$b=0.212112111211112 \ldots$

Here the decimal representation of $a$ and $b$ are non-terminating and non-repeating. So we observe that in first decimal place of $a$ and $b$ have the same digit 2 but digit in the second place of their decimal representation are distinct. And the number $a$ has 3 and $b$ has 1 . So $a>b$.

Hence two rational numbers are



lying between $0.232332333233332 \ldots$ and $0.212112111211112 \ldots$

Question 7: Give two rational numbers lying between $0.515115111511115 \ldots .0 .5353353335 \ldots$

Solution. Let $a=0.515115111511115 \ldots$ and $b=0.535335333533335 \ldots$

Here the decimal representation of $a$ and $b$ are non-terminating and non-repeating. So we observe that in first decimal place $a$ and $b$ have the same digit 5 but digit in the second place of their decimal representation are distinct. And the number a has 1 and $b$ has 3 . So $a
Hence two rational numbers are 0.5152,0.532 lying between $0.515115111511115 \ldots$ and $0.535335333533335 \ldots$

Question 8: Find one irrational number between $0.2101$ and $0.222 \ldots=0 . \overline{2}$

Solution. Let

$a=0.2101$

$b=0.2222 \ldots=0 . \overline{2}$

Here $a$ and $b$ are rational numbers .Since a has terminating and $b$ has repeating decimal. We observe that in second decimal place a has 1 and $b$ has 2 . So $a
Hence one irrational number is 0.2201001000100000... lying between $0.2101$ and $0.2222 \ldots$

Question 9 : Find a rational number and also an irrational number lying between the numbers $0.3030030003 \ldots$ and $0.3010010001$ $\cdots$

Solution. Let

$a=0.3030030003 \ldots$

$b=0.3010010001 \ldots$

Here decimal representation of $a$ and $b$ are non-terminating and non-repeating. So $a$ and $b$ are irrational numbers. We observe that in first two decimal place of $a$ and $b$ have the same digit but digit in the third place of their decimal representation is distinct.

Therefore, $a>b$.

Hence one rational number is 0.3011 lying between $0.3030030003 \ldots$ and $0.3010010001 \ldots$

And irrational number is $0.3020200200020000 \ldots$ lying between $0.3030030003 \ldots$ and $0.3010010001 \ldots$

Question 10 : Find three different irrational numbers between the rational numbers $\frac{5}{7}$ and $\frac{9}{11}$.

Solution. Let $x=\frac{5}{7}=0 . \overline{714285}$ and $y=\frac{9}{11}=0 . \overline{81}$

Here we observe that in the first decimal $x$ has digit 7 and $y$ has 8 . So $x
$a=0.72072007200072 .$

$b=0.73073007300073 .$

$c=0.74074007400074 \ldots .$

We find that

x
Hence a,b,c are required irrational numbers.

Question 11: Give an example of each, of two irrational numbers whose:

(i) difference is a rational number.

(ii) difference is an irrational number.

(iii) sum is a rational number.

(iv) sum is an irrational number.

(v) product is an rational number.

(vi) product is an irrational number.

(vii) quotient is a rational number.

(viii) quotient is an irrational number.

Solution. (i) Let $\sqrt{2}, 1+\sqrt{2}$

And, so $1+\sqrt{2}-\sqrt{2}=1$

Therefore, $\sqrt{2}$ and $1+\sqrt{2}$ are two irrational numbers and their difference is a rational number

(ii) Let $4 \sqrt{3}, 3 \sqrt{3}$ are two irrational numbers and their difference is an irrational number

Because $4 \sqrt{3}-3 \sqrt{3}=\sqrt{3}$ is an irrational number

(iii) Let $\sqrt{5},-\sqrt{5}$ are two irrational numbers and their sum is a rational number

That is $\sqrt{5}+(-\sqrt{5})=0$

(iv) Let $2 \sqrt{5}, 3 \sqrt{5}$ are two irrational numbers and their sum is an irrational number

That is $2 \sqrt{5}+3 \sqrt{5}=5 \sqrt{5}$

(v) Let $\sqrt{8}, \sqrt{2}$ are two irrational numbers and their product is a rational number

That is $\sqrt{8} \times \sqrt{2}=\sqrt{16}=4$

(vi) Let $\sqrt{2}, \sqrt{3}$ are two irrational numbers and their product is an irrational number

That is $\sqrt{2} \times \sqrt{3}=\sqrt{6}$

(vii) Let $\sqrt{8}, \sqrt{2}$ are two irrational numbers and their quotient is a rational number

That is $\frac{\sqrt{8}}{\sqrt{2}}=\frac{2 \sqrt{2}}{\sqrt{2}}=2$

(viii) Let $\sqrt{2}, \sqrt{3}$ are two irrational numbers and their quotient is an irrational number

That is $\sqrt{2} \div \sqrt{3}=\frac{\sqrt{2}}{\sqrt{3}}$

Question 12: Find two irrational numbers between $0.5$ and $0.55$.

Solution. Let

$a=0.5$

$b=0.55$ Here $a$ and $b$ are rational number. So we observe that in first decimal place $a$ and $b$ have same digit .So $a


Question 13: Find two irrational numbers lying between $0.1$ and $0.12$.

Solution. Let

$a=0.1$

$b=0.12$

Here $a$ and $b$ are rational number. So we observe that in first decimal place $a$ and $b$ have same digit. So $a


Question 14: Prove that $\sqrt{3}+\sqrt{5}$ is an irrational number.

Solution. Given that $\sqrt{3}+\sqrt{5}$ is an irrational number

Now we have to prove $\sqrt{3}+\sqrt{5}$ is an irrational number

Let $x=\sqrt{3}+\sqrt{5}$ is a rational

Squaring on both sides

$\Rightarrow x^{2}=(\sqrt{3}+\sqrt{5})^{2}$

$\Rightarrow x^{2}=(\sqrt{3})^{2}+(\sqrt{5})^{2}+2 \sqrt{3} \times \sqrt{5}$

$\Rightarrow x^{2}=3+5+2 \sqrt{15}$

$\Rightarrow x^{2}=8+2 \sqrt{15}$

$\Rightarrow \frac{x^{2}-8}{2}=\sqrt{15}$

Now $x$ is rational

$\Rightarrow x^{2}$ is rational

$\Rightarrow \frac{x^{2}-8}{2}$ is rational

$\Rightarrow \sqrt{15}$ is rational

But, $\sqrt{15}$ is an irrational

Thus we arrive at contradiction that $\sqrt{3}+\sqrt{5}$ is a rational which is wrong.

Hence $\sqrt{3}+\sqrt{5}$ is an irrational

Question 1: Complete the following sentences:

(i) Every point on the number line corresponds to a .... number which many be either ... or ...

(ii) The decimal form of an irrational number is neither $\ldots$ nor $\ldots$

(iii) The decimal representation of a rational number is either $\ldots$ or $\ldots$

(iv) Every real number is either .. number or ... number.

Solution. (i) Every point on the number line corresponds to a real number which may be either rational or an $\underline{\text { irrational number. }}$

(ii) The decimal form of an irrational number is neither terminating nor repeating.

(iii) The decimal representation of rational number is either terminating, recurring.

(iv) Every real number is either rational number or an irrational number because rational or an irrational number is a family of real number.

Question 2: Find whether the following statement are true or false.



(i) Every real number is either rational or irrational.

(ii) $\pi$ is an irrational number.

(iii) Irrational numbers cannot be represented by points on the number line.

Solution. (i) True, because rational or an irrational number is a family of real number. So every real number is either rational or an irrational number.

(ii) True, because the decimal representation of an irrational is always non-terminating or non-repeating. So $\pi=3.141 \ldots$ is an irrational number.

(iii) False, because we can represent irrational numbers by points on the number line.

Question 3: Represent $\sqrt{6}, \sqrt{7}, \sqrt{8}$ on the number line.

Solution. We are asked to represent $\sqrt{6}, \sqrt{7}$ and $\sqrt{8}$ on the number line

We will follow certain algorithm to represent these numbers on real line

We will consider point $A$ as reference point to measure the distance



(1) First of all draw a line $A X$ and $Y Y$ ' perpendicular to $A X$

(2) Consider $A O=2$ unit and $O B=1$ unit, so

$A B=\sqrt{2^{2}+1^{2}}$

$=\sqrt{5}$

(3) Take $A$ as center and $A B$ as radius, draw an arc which cuts line $A X$ at $A_{1}$

(4) Draw a perpendicular line $A_{1} B_{1}$ to $A X$ such that $A_{1} B_{1}=1$ unit and

(5) Take $A$ as center and $A B_{1}$ as radius and draw an arc which cuts the line $A X$ at $A_{2}$.

Here

$A B_{1}=A A_{2}$

$=\sqrt{A A_{1}^{2}+A_{1} B_{1}^{2}}$

$=\sqrt{(\sqrt{5})^{2}+1}$

$=\sqrt{6}$ unit

So $A A_{2}=\sqrt{6}$ unit

So $A_{2}$ is the representation for $\sqrt{6}$

(1) Draw line $A_{2} B_{2}$ perpendicular to $A X$

(2) Take $A$ center and $A B_{2}$ as radius and draw an arc which cuts the horizontal line at $A 3$ such that

$A B_{2}=A A_{3}$

$=\sqrt{A A_{2}^{2}+A_{2} B_{2}^{2}}$

$=\sqrt{(\sqrt{6})^{2}+1}$

$=\sqrt{7}$ unit

So point $A 3$ is the representation of $\sqrt{7}$

(3) Again draw the perpendicular line $A_{3} B_{3}$ to $A X$

(4) Take $A$ as center and $A B 3$ as radius and draw an arc which cuts the horizontal line at $A 4$

Here;

$A B_{3}=A A_{4}$

$=\sqrt{A A_{3}^{2}+A_{3} B_{3}^{2}}$

$=\sqrt{(\sqrt{7})^{2}+1^{2}}$

$=\sqrt{8}$ unit

$A_{4}$ is basically the representation of $\sqrt{8}$

Question 4: Represent $\sqrt{3.5}, \sqrt{9.4}, \sqrt{10.5}$ on the real number line.

Solution. We are asked to represent the real numbers $\sqrt{3.5}, \sqrt{9.4}$ and $\sqrt{10.5}$ on the real number line

We will follow a certain algorithm to represent these numbers on real number line



(a) $\sqrt{3.5}$

We will take $A$ as reference point to measure the distance

(1) Draw a sufficiently large line and mark a point $A$ on it

(2) Take a point $B$ on the line such that $A B=3.5 \mathrm{~cm}$

(3) Mark a point $C$ on the line such that $B C=1 \mathrm{~cm}$

(4) Find mid point of $A B$ and let it be $O$

(5) Take $O$ as center and $O C$ as radius and draw a semi circle. Draw a perpendicular $B D$ which cuts the semi circle at $D$

(6) Take $B$ as the center and $B D$ as radius, draw an arc which cuts the horizontal line at $E$

(7) Point $E$ is the representation of $\sqrt{3.5}$

(b) $\sqrt{9.4}$

We will take $A$ as reference point to measure the distance. We will follow the same figure in the part (a)

(1) Draw a sufficiently large line and mark a point $A$ on it

(2) Take a point $B$ on the line such that $A B=9.4 \mathrm{~cm}$

(3) Mark a point $C$ on the line such that $B C=1 \mathrm{~cm}$

(4) Find mid point of $A B$ and let it be $O$

(5) Take $O$ as center and $O C$ as radius and draw a semi circle. Draw a perpendicular $B C$ which cuts the semi circle at $D$

(6) Take $B$ as the center and $B D$ as radius, draw an arc which cuts the horizontal line at $E$

(7) Point $E$ is the representation of $\sqrt{9.4}$

(c) $\sqrt{10.5}$

We will take $A$ as reference point to measure the distance. We will follow the same figure in the part (a)

(1) Draw a sufficiently large line and mark a point $A$ on

(2) Take a point $B$ on the line such that $A B=10.5 \mathrm{~cm}$

(3) Mark a point $C$ on the line such that $B C=1 \mathrm{~cm}$

(4) Find mid point of $A B$ and let it be $O$

(5) Take $O$ as center and $O C$ as radius and draw a semi circle. Draw a perpendicular $B C$ which cuts the semi circle at $D$

(6) Take $B$ as the center and $B D$ as radius, draw an arc which cuts the horizontal line at $E$

(7) Point $E$ is the representation of $\sqrt{10.5}$

Question 1: Visualise $2.665$ on the number line, using successive magnification.

Solution.





We know that $2.665$ lies between 2 and $3 .$ So, we divide the number line into 10 equal parts and mark each point of division. The first mark on the right of 2 will be $2.1$ followed by $2.2$ and so on. The point left of 3 will be $2.9$. Now, the magnified view of this will show that $2.665$ lies between $2.6$ and 2.7. So, our focus will be now $2.6$ and $2.7 .$ We divide this again into 10 equal parts. The first part will be $2.61$ followed by $2.62$ and so on.

We now magnify this again and find that $2.665$ lies between $2.66$ and $2.67 .$ So, we magnify this portion and divide it again into 10 equal parts. The first part will represent $2.661$, next will be $2.662$ and so on. So, $2.665$ will be 5 th mark in this subdivision as shown in the figure.

Question 2: Visualise the representation of $5.3 \overline{7}$ on the number line upto 5 decimal places, that is upto $5.37777 .$

Solution.



We know that $5.3 \overline{7}$ will lie between 5 and $6 .$ So, we locate $5.3 \overline{7}$ between 5 and 6 . We divide this portion of the number line between 5 and 6 into 10 equal parts and use a magnifying glass to visualize $5.3 \overline{7}$.

$5.3 \overline{7}$ lies between $5.37$ and $5.38$. To visualize $5.3 \overline{7}$ more accurately we use a magnifying glass to visualize between $5.377$ and $5.378$ Again, we divide the portion between $5.377$ and $5.378$ into 10 equal parts and visualize more closely to represent $5.3 \overline{7}$ as given in the figure. This is located between $5.3778$ and $5.3777$

Question 1: Mark the correct alternative in each of the following:

1. Which one of the following is a correct statement?

(a) Decimal expansion of a rational number is terminating

(b) Decimal expansion of a rational number is non-terminating

(c) Decimal expansion of an irrational number is terminating

(d) Decimal expansion of an irrational number is non-terminating and non-repeating

Solution. The decimal expansion of an irrational number is non-terminating and non- repeating. Thus, we can say that a number, whose decimal expansion is non-terminating and non- repeating, called irrational number. And the decimal expansion of rational number is either terminating or repeating. Thus, we can say that a number, whose decimal expansion is either terminating or repeating, is called a rational number.

Hence the correct option is d.

Question 2: Which one of the following statements is true?

(a) The sum of two irrational numbers is always an irrational number

(b) The sum of two irrational numbers is always a rational number

(c) The sum of two irrational numbers may be a rational number or an irrational number

(d) The sum of two irrational numbers is always an integer

Solution. Since, $-\sqrt{2}$ and $\sqrt{2}-1$ are two irrational number and $-\sqrt{2}+(\sqrt{2}+1)=1$

Therefore, sum of two irrational numbers may be rational

Now, let $\sqrt{3}$ and $\sqrt{2}-\sqrt{3}$ be two irrational numbers and $\sqrt{3}+(\sqrt{2}-\sqrt{3})=\sqrt{2}$

Therefore, sum of two irrational number may be irrational

$$\text { Hence the correct option is } c \text {. }$$

Question 3: Which of the following is a correct statement?

(a) Sum of two irrational numbers is always irrational

(b) Sum of a rational and irrational number is always an irrational number

(c) Square of an irrational number is always a rational number

(d) Sum of two rational numbers can never be an integer

Solution. The sum of irrational number and rational number is always irrational number.

Let a be a rational number and b be an irrational number.

Then,

$(a+b)^{2}=a^{2}+b^{2}+2 a b$

$=\left(a^{2}+b^{2}\right)+2 a b$

As $2 a b$ is irrational therefore $(a+b)^{2}$ is irrational.

Hence $(a+b)$ is irrational.

Therefore answer is b.

Question 4: Which of the following statements is true?

(a) Product of two irrational numbers is always irrational

(b) Product of a rational and an irrational number is always irrational

(c) Sum of two irrational numbers can never be irrational (d) Sum of an integer and a rational number can never be an integer

Solution. Since we know that the product of rational and irrational number is always an irrational. For example: Let $\frac{1}{2}, \sqrt{3}$ are rational and irrational

numbers respectively and their product is $\frac{\sqrt{3}}{2}$

Hence the correct option is b.

Question 5: Which of the following is irrational?

(a) $\sqrt{\frac{4}{9}}$

(b) $\sqrt{\frac{4}{5}}$

(c) $\sqrt{7}$

(d) $\sqrt{81}$

Solution. Given that

$\sqrt{\frac{4}{9}}=\frac{2}{3}$

$\frac{4}{5}=0.8$

$\sqrt{81}=9$

And 7 is not a perfect square.

Hence the correct option is c.

Question 6: Which of the following is irrational?

(i) $0.14$

(ii) $0.14 \overline{16}$

(iii) $0 . \overline{1416}$

(iv) $0.1014001400014 \ldots$

Solution. Given that

$0.14$

$0.141 \overline{6}$

$0 . \overline{1416}$

$0.1014001400014 \ldots$

Here $0.1014001400014 \ldots .$ is non-terminating or non-repeating. So it is an irrational number.

Hence the correct option is d.

Question 7: Which of the following is rational?

(a) $\sqrt{3}$

(b) $\pi$

(c) $\frac{4}{0}$

(d) $\frac{0}{4}$

Solution. Given that $\sqrt{3}, \pi, \frac{4}{0}$ and $\frac{0}{4}$

Here, $\frac{0}{4}=0$, this is the form of $\frac{p}{q}$. So this is a rational number

Hence the correct option is d.

Question 8: The number $0.318564318564318564 \ldots \ldots . .$ is:

(a) a natural number

(b) an integer

(c) a rational number

(d) an irrational number

Solution. Since the given number $0.318564318564318564 \ldots=0 . \overline{318564}$ is repeating, so it is rational number because rational number is always either terminating or repeating

Hence the correct option is C.

Question 9: If $n$ is a natural number, then $\sqrt{n}$ is

(a) always a natural number

(b) always an irrational number

(c) always an irrational number

(d) sometimes a natural number and sometimes an irrational number

Solution. The term "natural number" refers either to a member of the set of positive integer $1,2,3 .$ And natural number starts from one of counting digit. Thus, if $n$ is a natural number then sometimes $n$ is a perfect square and sometimes it is not.

Therefore, sometimes $\sqrt{n}$ is a natural number and sometimes it is an irrational number

Hence the correct option is d.

Question 10: Which of the following numbers can be represented as non-terminating, repeating decimals?

Solution. (a) $\frac{39}{24}$

(b) $\frac{3}{16}$

(c) $\frac{3}{11}$

(d) $\frac{137}{25}$

Solution. Given that

$\frac{39}{24}=1.625$

$\frac{3}{16}=0.1875$

$\frac{3}{11}=0.272727272$

$\frac{1.37}{25}=0.0548$

Here $\frac{3}{11}$ is repeating but non-terminating.

Hence the correct option is C.

Question 11: Every point on a number line represents

(a) a unique real number

(b) a natural number

(c) a rational number

(d) an irrational number

Solution. In basic mathematics, number line is a picture of straight line on which every point is assumed to correspond to real number.

Hence the correct option is a.

Question 12: Which of the following is irrational?

(a) $0.15$

(b) $0.01516$

(c) $0 . \overline{1516}$

(d) $0.5015001500015$.

Solution. Given decimal numbers are

$0.15,0.1516,0 . \overline{1516}$ and $0.501500115000115 \ldots$

Here the number $0.501500115000115 \ldots$ is non terminating or non-repeating.

Hence the correct option is d.

Question 14: The number $0 . \overline{3}$ in the form $\frac{p}{q}$, where $p$ and $q$ are integers and $q \neq 0$, is

(a) $\frac{33}{100}$

(b) $\frac{3}{10}$

(c) $\frac{1}{3}$

(d) $\frac{3}{100}$

Solution. Given number is $0 . \overline{3}$

$0 . \overline{3}=0+\frac{3}{9}$

$=\frac{3}{9}$



The correct option is C.

Question 15: 0. $3 \overline{2}$ when expressed in the form $\frac{p}{q}(p, q$ are integers $q \neq 0)$, is

(a) $\frac{8}{25}$

(b) $\frac{29}{90}$

(c) $\frac{32}{99}$

(d) $\frac{32}{199}$

Solution. Given that $0.3 \overline{2}$

Now we have to express this number into $\frac{p}{q}$ form

Let $X=0.3 \overline{2}$

$10 x=3+0.2222$

$\Rightarrow 10 x=3+\frac{2}{9}$

$\Rightarrow 10 x=\frac{29}{9}$

$\Rightarrow x=\frac{29}{90}$

The correct option is B.

Question 16: 23. $\overline{43}$ when expressed in the form $\frac{p}{q}(p, q$ are integers $q \neq 0)$, is

(a) $\frac{2320}{99}$

(b) $\frac{2343}{100}$

(c) $\frac{2343}{999}$

(d) $\frac{2320}{199}$

Solution. Given that $23 . \overline{43}$



Now we have to express this number into the form of $\frac{p}{q}$

Let

$x=23.43$

$x=23+0.4343 \ldots$

$x=23+\frac{43}{99}$

$x=\frac{2277+43}{99}=\frac{2320}{99}$

$\Rightarrow 23 . \overline{43}=$

The correct option is A.

Question 17: $0 . \overline{001}$ when expressed in the form $\frac{p}{q}(p, q$ are integers, $q \neq 0)$, is

(a) $\frac{1}{1000}$

(b) $\frac{1}{100}$

(c) $\frac{1}{1999}$

(d) $\frac{1}{999}$

Solution. Given that $0 . \overline{001}$

Now we have to express this number into $\frac{p}{q}$ form

Let $x=0 . \overline{001}$

$=0+\frac{1}{999}$

$=\frac{1}{999}$

The correct option is D.

Question 18: The value of $0 . \overline{23}+0 . \overline{22}$ is

(a) $0 . \overline{45}$

(b) $0 . \overline{43}$

(c) $0 . \overline{45}$

(d) $0.45$

Solution. Given that $0 . \overline{23}+0 . \overline{22}$

Let $x=0 . \overline{23}+0 . \overline{22}$

Now we have to find the value of $x$

$\Rightarrow x=0 . \overline{23}+0 . \overline{22}$

$\Rightarrow x=\frac{23}{99}+\frac{22}{99}$

$\Rightarrow x=\frac{23+22}{99}$

$\Rightarrow x=\frac{45}{99}$

$\Rightarrow x=\frac{5}{11}$

$0 . \overline{23}+\overline{0.22}=0 . \overline{45}$

The correct option is A.

Question 19: An irrational number between 2 and $2.5$ is

(a) $\sqrt{11}$

(b) $\sqrt{5}$

(c) $\sqrt{22.5}$

(d) $\sqrt{12.5}$

Solution. Let

$$a=2$$

$b=2.5$

Here $a$ and $b$ are rational numbers. So we observe that in first decimal place $a$ and $b$ have distinct. According to question $a
Hence the correct answer is B.

Question 20: The number of consecutive zeros in $2^{3} \times 3^{4} \times 5^{4} \times 7$, is

(a) 3

(b) 2

(c) 4

(d) 5

Solution. We are given the following expression and asked to find out the number of consecutive zeros

$2^{3} \times 3^{4} \times 5^{4} \times 7$

We basically, will focus on the powers of 2 and 5 because the multiplication of these two number gives one zero. So

$2^{3} \times 3^{4} \times 5^{4} \times 7=2^{3} \times 5^{4} \times 3^{4} \times 7$

$=2^{3} \times 5^{3} \times 5 \times 3^{4} \times 7$

$=(2 \times 5)^{3} \times 5 \times 3^{4} \times 7$

$=10^{3} \times 5 \times 3^{4} \times 7$

$=5 \times 81 \times 7 \times 1000$

$=2835000$

Therefore the consecutive zeros at the last is 3

So the option (a) is correct

Question 21: The smallest rational number by which $\frac{1}{3}$ should be multiplied so that its decimal expansion terminates after one place of decimal, is

(a) $\frac{1}{10}$

(b) $\frac{3}{10}$

(c) 3

(d) 30

Solution. Give number is $\frac{1}{3}$. Now multiplying by $\frac{3}{10}$ in the given number, we have

$\frac{1}{3}=\frac{1}{3} \times \frac{3}{10}$

$\Rightarrow \frac{1}{3}=\frac{1}{10}$

$\Rightarrow \frac{1}{3}=0.1$

Hence the correct option is B.

Question 1: The decimal expansion of a rational number is either or_______ or______.

Solution. The decimal expansion of a rational number either terminates after finitely many digits or ends with a repeating sequence.

Hence, the decimal expansion of a rational number is either terminating or recurring.

Question 2: The decimal expansion of an irrational number is non-terminating and______.

Solution. The decimal expansion of a rational number either terminates after finitely many digits or ends with a repeating sequence.

In case of irrational number, the decimal expansion neither terminates nor repeats after finitely many digits.

Hence, the decimal expansion of an irrational number is non-terminating and non-repeating.

Question $3:$

The decimal expansion of $\sqrt{2}is_____________ and___________.

Solution. $\sqrt{2}$ is an irrational number.

The decimal expansion of an irrational number neither terminates nor repeats after finitely many digits.

Hence, the decimal expansion of $\sqrt{2}$ is non-terminating and non-repeating.

Question 4: The value of $1.999 .$ in the form of $\frac{m}{n}$, where $m$ and $n$ are integers and $n \neq 0$, is________.

Solution. Let $x=1.999 \ldots \ldots$ $\ldots(1)$

Multiply (1) by 10 on both sides, we get

$10 x=19.999 \ldots \ldots$ $\ldots(2)$

Subtracting (1) from (2), we get

$10 x-x=19.999 \ldots-1.999 \ldots$

$\Rightarrow 9 x=18$

$\Rightarrow x=\frac{18}{9}$

$\Rightarrow x=\frac{2}{1}$

Hence, the value of $1.999 \ldots$ in the form of $\frac{m}{n}$, where $m$ and $n$ are integers and $n \neq 0$, is $\frac{2}{1}$.

Question 5: Every recurring decimal is a__________ number.

Solution. The decimal expansion of a rational number either terminates after finitely many digits or ends with a repeating sequence.

Hence, every recurring decimal is a rational number.

Question $6:$

$\pi$ is an_________ number.

Solution. The decimal expansion of $\pi$ neither terminates nor repeats after finitely many digits.

Therefore, it is an irrational number.

Hence, $\pi$ is an irrational number.

Question 7: The product of a non-zero rational number with an irrational number is always an__________ number.

Solution. The product of a non-zero rational number with an irrational number always results in an irrational number.

Hence, the product of a non-zero rational number with an irrational number is always an irrational number.

Question 8: The simplest form of $1 . \overline{6}$ is____________.

Solution. Let $x=1.6666 \ldots \ldots$ $\ldots(1)$

Multiply (1) by 10 on both sides, we get

$10 x=16.6666 \ldots \ldots$ ... (2)

Subtracting (1) from (2), we get

$10 x-x=16.6666 \ldots-1.6666 \ldots$

$\Rightarrow 9 x=15$

$\Rightarrow x=\frac{15}{9}$

$\Rightarrow x=\frac{5}{3}$

Hence, the simplest form of $1 . \overline{6}$ is $\frac{5}{3}$.

Question 9 $0 . \overline{3}+0 . \overline{4}$ is equal to___________.

Solution. Let $x=0.3333 \ldots \ldots$ $\cdots(1)$

Multiply (1) by 10 on both sides, we get

$10 x=3.3333 \ldots \ldots$ $\ldots(2)$

Subtracting (1) from (2), we get

$10 x-x=3.333 \ldots-0.333 \ldots$

$\Rightarrow 9 x=3$

$\Rightarrow x=\frac{3}{9}$ $\ldots(3)$

Let $y=0.4444 \ldots \ldots$ $\ldots(4)$

Multiply (1) by 10 on both sides, we get

$10 y=4.4444 \ldots \ldots$ $\ldots(5)$

Subtracting $(4)$ from $(5)$, we get

$10 y-y=4.4444 \ldots-0.4444 \ldots$

$\Rightarrow 9 y=4$

$\Rightarrow y=\frac{4}{9}$ $\ $\ldots(6)$

Now,

$0 . \overline{3}+0 . \overline{4}=x+y$

$=\frac{3}{9}+\frac{4}{9} \quad$ (From (3) and (6) $)$

$=\frac{7}{9}$

Hence, $0 . \overline{3}+0 . \overline{4}$ is equal to $\frac{7}{9}$.

Question 10: The sum of a rational number and an irrational number is___________ number.

Solution. The sum of a rational number and an irrational number always results in an irrational number.

Hence, the sum of a rational number and an irrational number is an irrational number.

Question 11: Every real number is either ________ or _______ number.

Solution. The real number includes all the rational as well as irrational numbers.

Hence, every real number is either rational or irrational number.

Question 1: Is zero a rational number? Can you write it in the form $\frac{p}{q}$, where $p$ and $q$ are integers and $q \neq 0 ?$

Solution. Yes, zero is a rational number because it is either terminating or non-terminating so we can write in the form of $\frac{p}{q}$, where $p$ and $q$ are natural numbers and $q$ is not equal to zero.

So,

$p=0, q=1,2,3 \ldots$

Therefore,

$\frac{p}{q}=\frac{0}{1}$ or $\frac{0}{2}$ or $\frac{0}{3} \ldots$

Question 2: Find five rational numbers between 1 and 2.

Solution. We need to find 5 rational numbers between 1 and $2 .$

Consider,

$1=\frac{1}{1}$

$\Rightarrow 1=\frac{1}{1} \times \frac{6}{6}$

$\Rightarrow 1=\frac{6}{6}$

And

$\Rightarrow 2=\frac{2}{1}$

$\Rightarrow 2=\frac{2}{1} \times \frac{6}{6}$

$\Rightarrow 2=\frac{12}{6}$

So, five rational numbers between $\frac{6}{6}$ and $\frac{12}{6}$ will be $\frac{7}{6}, \frac{8}{6}, \frac{9}{6}, \frac{10}{6}, \frac{11}{6}$.

Hence 5 rational numbers between 1 and 2 are:



Question 3: Find six rational numbers between 3 and 4.

Solution. We need to find 6 rational numbers between 3 and 4.

Consider,

$3=\frac{3}{1}$

$\Rightarrow 3=\frac{3}{1} \times \frac{7}{7}$

$\Rightarrow 3=\frac{21}{7}$

And

$4=\frac{4}{1}$

$\Rightarrow 4=\frac{4}{1} \times \frac{7}{7}$

$\Rightarrow 4=\frac{28}{7}$

So, six rational numbers between $\frac{21}{7}$ and $\frac{28}{7}$ will be



Hence 6 rational numbers between 3 and 4 are



Question 4: Find five rational numbers between $\frac{3}{5}$ and $\frac{4}{5}$.

Solution. We need to find 5 rational numbers between $\frac{3}{5}$ and $\frac{4}{5}$

Since, LCM of denominators $=\operatorname{LCM}(5,5)=5$

So, consider

$\frac{3}{5}=\frac{3}{5} \times \frac{6}{6}$

$\Rightarrow \frac{3}{5}=\frac{18}{30}$

And,

$\Rightarrow \frac{4}{5}=\frac{4}{5} \times \frac{6}{6}$

$\Rightarrow \frac{4}{5}=\frac{24}{30}$

Hence 5 rational numbers between $\frac{3}{5}$ and $\frac{4}{5}$ are:



Question 5: Are the following statements true or false? Give reasons for your answer.

(i) Every whole number is a natural number.

(ii) Every integer is a rational number.

(iii) Every rational number is an integer.

(iv) Every natural number is a whole number.

(v) Every integer is a whole number.

(vi) Every rational number is a whole number.

Solution. (i) False, because whole numbers start from zero and natural numbers start from one

(ii) True, because it can be written in the form of a fraction with denominator 1

(iii) False, rational numbers are represented in the form of fractions. Integers can be represented in the form of fractions but all fractions are not integers. for example: $\frac{3}{4}$ is a rational number but not an integer.

(iv) True, because natural numbers belong to whole numbers

(v) False, because set of whole numbers contains only zero and set of positive integers, whereas set of integers is the collection of zero and all positive and negative integers.

(vi) False, because rational numbers include fractions but set of whole number does not include fractions.

So, that’s all from this article. I hope you enjoyed this post. If you found this article helpful then please share it with other students.

Also Read,

Download NCERT Class 9 Maths Chapterwise Book Free

Download NCERT Class 10 Maths Chapterwise Book Free

Download NCERT Class 9 Maths Chapterwise Exemplar Free

Download NCERT Class 10 Maths Chapterwise Exemplar Free

If you have any Confusion related to RD Sharma Solutions for Class 9 Maths Chapter 1 Number System then feel free to ask in the comments section down below.

To watch Free Learning Videos on Class 9 by Kota’s top Faculties Install the eSaral App