RD Sharma Solutions for Class 9 Maths Chapter 2 Exponents of Real Numbers - Free PDF Download

Hey, are you a class 9 student and looking for ways to download RD Sharma Solutions for Class 9 Maths Chapter 2 "Exponents of Real Numbers"? If yes. Then read this post till the end.

In this article, we have listed RD Sharma Solutions for Class 9 Maths Chapter 2 in PDF that is prepared by Kota’s top IITian’s Faculties by keeping Simplicity in mind.

If you want to learn and understand class 9 Maths Chapter 2 "Exponents of Real Numbers" in an easy way then you can use these solutions PDF.

Chapter 2 of RD Sharma Class 9 deals with rational exponents of real numbers and laws of rational exponents. If you want to improve your basic fundamentals of Exponents of Real Numbers then you can use this.

RD Sharma Solutions helps students to Practice important concepts of subjects easily. RD Sharma class 9 solutions provide detailed explanations of all the  exercise questions that students can use to clear their doubts instantly.

If you want to become good at Math then it is very important for you to have a good knowledge of all the important topics of class 9 math, so to learn and practice those topics you can use eSaral RD Sharma Solutions.

In this article, we have listed RD Sharma Solutions for Class 9 Maths Chapter 2 that you can download to start your preparations anytime.

So, without wasting more time Let’s start.

RD Sharma Solutions for Class 9 Maths Chapter 2 Exponents of Real Numbers - Free PDF Download

Question 1: Simplify the following

(i) $3\left(a^{4} b^{3}\right)^{10} \times 5\left(a^{2} b^{2}\right)^{3}$

(ii) $\left(2 x^{-2} y^{3}\right)^{3}$

(iii) $\frac{\left(4 \times 10^{7}\right)\left(6 \times 10^{-5}\right)}{8 \times 10^{4}}$

(iv) $\frac{4 a b^{2}\left(-5 a b^{3}\right)}{10 a^{2} b^{2}}$

$(v)\left(\frac{x^{2} y^{2}}{a^{2} b^{3}}\right)^{n}$

(vi) $\frac{\left(a^{3 n-9}\right)^{6}}{a^{2 n-4}}$

Solution. Using laws: $\left(a^{m}\right)=a^{m n}, a^{0}=1, a^{m}=1 / a$ and $\left.a^{m} \times a^{n}=a^{m+n}\right]$ (i) $3\left(a^{4} b^{3}\right)^{10} \times 5\left(a^{2} b^{2}\right)^{3}$

On simplifying the given equation, we get;

$=3\left(a^{40} b^{30}\right) \times 5\left(a^{\circ} b^{c}\right)$

$=15\left(a^{40} b^{36}\right)$

[using laws: $\left(a^{m}\right)^{n}=a^{m n}$ and $\left.a^{m} \times a^{n}=a^{m+n}\right]$

(ii) $\left(2 x^{-2} y^{3}\right)^{3}$

On simplifying the given equation, we get;

$=\left(2^{3} \mathrm{X}^{-2 \times 3} \mathrm{y}^{3 \times 3}\right)$

$=8 x^{-0} y^{9}$

(iii) $\frac{\left(4 \times 10^{7}\right)\left(6 \times 10^{-5}\right)}{8 \times 10^{4}}$

$=\frac{\left(24 \times 10^{7} \times 10^{-5}\right)}{8 \times 10^{4}}$

$=\frac{\left(24 \times 10^{7-5}\right)}{8 \times 10^{4}}$

$=\frac{\left(24 \times 10^{2}\right)}{8 \times 10^{4}}$

$=\frac{\left(3 \times 10^{2}\right)}{10^{4}}$

$=\frac{3}{100}$

(iv) $\frac{4 a b^{2}\left(-5 a b^{3}\right)}{10 a^{2} b^{2}}$

$=\frac{4 \times(-5)}{10}$

$\times a^{1+1-2} b^{2+3-2}$

$=-2 \times a^{0} b^{3}$

$=-2 b^{3}$

$(v)\left(\frac{x^{2} y^{2}}{a^{2} b^{3}}\right)^{n}$

$=\frac{x^{2 n} \times y^{2 n}}{a^{2 n} b^{3 n}}$

$=\frac{x^{2 n} \times y^{2 n}}{a^{2 n} b^{3 n}}$

(vi) $\frac{\left(a^{3 n-9}\right)^{6}}{a^{2 n-4}}$

$=\frac{a^{(3 n-9) 6}}{a^{2 n-4}}$

$=\frac{a^{18 n-54}}{a^{2 n-4}}$

$=a^{18 n-54-2 n+4}$

$=a^{16 n-50}$

Question 2: If $a=3$ and $b=-2$, find the values of:

(i) $\mathbf{a}^{a}+b^{b}$

(ii) $\mathbf{a}^{\mathrm{b}}+\mathbf{b}^{\mathrm{a}}$

(iii) $(\mathrm{a}+\mathrm{b})^{\mathrm{ab}}$

Solution. (i) $a^{a}+b^{b}$

Now putting the values of ' $a$ ' and ' $b$ ', we get;

$=3^{3}+(-2)^{-2}$

$=3^{3}+(-1 / 2)^{2}$

$=27+1 / 4$

$=109 / 4$ (ii) $a^{b}+b^{a}$

Now putting the values of 'a' and ' $b$ ', we get;

$=3^{-2}+(-2)^{3}$

$=(1 / 3)^{2}+(-2)^{3}$

$=1 / 9-8$

$=-71 / 9$

(iii) $(\mathrm{a}+\mathrm{b})^{\mathrm{ab}}$

Now putting the values of 'a' and ' $b$ ', we get;

$=(3+(-2))^{3(-2)}$

$=(3-2))^{-6}$

$=1^{-6}$

$=1$

Question 3: Prove that



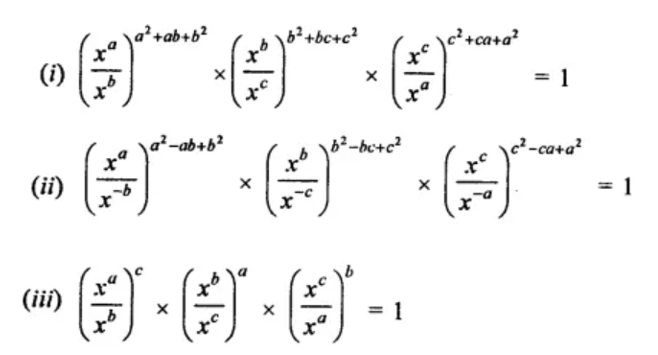
Solution. (i) $L . H . S .=$

$\frac{x^{a^{3}+a^{2} b+a b^{2}}}{x^{a^{2} b+a b^{2}+b^{3}}}$

$\times \frac{x^{b^{3}+b^{2} c+b c^{2}}}{x^{b^{2} c+b c^{2}+c^{3}}}$

$\times \frac{x^{c^{3}+c^{2} a+c a^{2}}}{x^{c^{2} a+c a^{2}+a^{3}}}$

$=x^{a^{3}+a^{2} b+a b^{2}-\left(b^{3}+a^{2} b+a b^{2}\right)}$

$\times x^{b^{3}+b^{2} c+b c^{2}-\left(c^{3}+b^{2} c+b c^{2}\right)}$

$\times x^{c^{3}+c^{2} a+c a^{2}-\left(a^{3}+c^{2} a+c a^{2}\right)}$

$=x^{a^{3}-b^{3}} \times x^{b^{3}-c^{3}} \times x^{c^{3}-a^{3}}$

$=x^{a^{3}-b^{3}+b^{3}-c^{3}+c^{3}-a^{3}}$

$=x^{0}$

$=1$

= R.H.S.

(ii) We have to prove here;

$\left(\frac{x^{a}}{x^{-b}}\right)^{a^{2}-a b+b^{2}}$

$\times\left(\frac{x^{b}}{x^{-c}}\right)^{b^{2}-b c+c^{2}}$

$\times\left(\frac{x^{c}}{x^{-a}}\right)^{c^{2}-c a+a^{2}}$

$=x^{2\left(a^{3}+b^{3}+c^{3}\right)}$

L.H.S. $=$

$=x^{(a+b)\left(a^{2}-a b+b^{2}\right)}$

$\times x^{(b+c)\left(b^{2}-b c+c^{2}\right)}$

$\times x^{(c+a)\left(c^{2}-c a+a^{2}\right)}$

$=x^{a^{3}+b^{3}} \times x^{b^{3}+c^{3}} \times x^{c^{3}+a^{3}}$ $=x^{a^{3}+b^{3}+b^{3}+c^{3}+c^{3}+a^{3}}$

$=x^{2\left(a^{3}+b^{3}+c^{3}\right)}$

$=\text { R.H.S. }$

(iii) L.H.S. =

$\left(\frac{x^{a}}{x^{b}}\right)^{c} \times\left(\frac{x^{b}}{x^{c}}\right)^{a} \times\left(\frac{x^{c}}{x^{a}}\right)^{b}$

$=\left(\frac{x^{a c}}{x^{b c}}\right) \times\left(\frac{x^{b a}}{x^{c a}}\right) \times\left(\frac{x^{b c}}{x^{a b}}\right)$

$=x^{a c-b c} \times x^{b a-c a} \times x^{b c-a b}$

$=x^{a c-b c+b a-c a+b c-a b}$

$=x^{0}$

$=1$

Question 4: Prove that

(i) $\frac{1}{1+x^{a-b}}+\frac{1}{1+x^{b-a}}=1$

(ii) $\frac{1}{1+x^{b-a}+x^{c-a}}+\frac{1}{1+x^{a-b}+x^{c-b}}+\frac{1}{1+x^{b-c}+x^{a-c}}$

Solution: (i) L.H.S

$=\frac{1}{1+\frac{x^{a}}{x^{b}}}+\frac{1}{1+\frac{x^{b}}{x^{a}}}$

$=\frac{x^{b}}{x^{b}+x^{a}}+\frac{x^{a}}{x^{a}+x^{b}}$

$=\frac{x^{b}+x^{a}}{x^{a}+x^{b}}$

$=1$

= R.H.S.

(ii) L.H.S

$=\frac{1}{1+\frac{x^{b}}{x^{a}}+\frac{x^{c}}{x^{a}}}$

$+\frac{1}{1+\frac{x^{a}}{x^{b}}+\frac{x^{c}}{x^{b}}}$

$+\frac{1}{1+\frac{x^{b}}{x^{c}}+\frac{x^{a}}{x^{c}}}$

$=\frac{x^{a}}{x^{a}+x^{b}+x^{c}}$

$+\frac{x^{b}}{x^{b}+x^{a}+x^{c}}$

$+\frac{x^{c}}{x^{c}+x^{b}+x^{a}}$

$=\frac{x^{a}+x^{b}+x^{c}}{x^{a}+x^{b}+x^{c}}$

$=1$

$=\text { R.H.S. }$

Question 5: Prove that

(i) $\frac{a+b+c}{a^{-1} b^{-1}+b^{-1} c^{-1}+c^{-1} a^{-1}}=a b c$

(ii) $\left(a^{-1}+b^{-1}\right)^{-1}=\frac{a b}{a+b}$

Solution: (i) L.H.S.

$=\frac{a+b+c}{\frac{1}{a b}+\frac{1}{b c}+\frac{1}{c a}}$

$=\frac{a+b+c}{\frac{a+b+c}{a b c}}$

$=a b c$

= R.H.S.

(ii) L.H.S.

$=\frac{1}{\left(a^{-1}+b^{-1}\right)}$

$=\frac{1}{\left(\frac{1}{a}+\frac{1}{b}\right)}$

$=\frac{1}{\left(\frac{a+b}{a b}\right)}$

$=\frac{a b}{a+b}$

$\text { = R.H.S. }$

Question 6: If $a b c=1$, show that

$\frac{1}{1+a+b^{-1}}+\frac{1}{1+b+c^{-1}}+\frac{1}{1+c+a^{-1}}=1$

Solution: $=\frac{1}{1+a+\frac{1}{b}}$

$+\frac{1}{1+b+\frac{1}{c}}$

$+\frac{1}{1+c+\frac{1}{a}}$

$=\frac{b}{b+a b+1}$

$+\frac{c}{c+b c+1}$

$+\frac{a}{a+a c+1}$$\ldots(1)$

Given, $a b c=1$

So, $c=1 / a b$

By putting the value $c$ in equation (1)

$=\frac{b}{b+a b+1}$

$+\frac{\frac{1}{a b}}{\frac{1}{a b}+b\left(\frac{1}{a b}\right)+1}$

$+\frac{a}{a+a\left(\frac{1}{a b}\right)+1}$c

$=\frac{b}{b+a b+1}$

$+\frac{\frac{1}{a b} \times a b}{1+b+a b}$

$+\frac{a b}{1+a b+b}$

$=\frac{b}{b+a b+1}$

$+\frac{1}{1+b+a b}$

$+\frac{a b}{1+a b+b}$

$=\frac{1+a b+b}{b+a b+1}$

$=1$

Exercise $2.2$

Question 1: Assuming that $\mathrm{x}, \mathrm{y}, \mathrm{z}$ are positive real numbers, simplify each of the following:

(i) $\left(\sqrt{\left(x^{-3}\right)}\right)^{5}$

(ii) $\sqrt{x^{3} y^{-2}}$

(iii) $\left(x^{-\frac{2}{3}} y^{-\frac{1}{2}}\right)^{2}$

(iv) $(\sqrt{x})^{-\frac{2}{3}} \sqrt{y^{4}} \div \sqrt{x y^{-\frac{1}{2}}}$

(v) $\sqrt[5]{243 x^{10} y^{5} z^{10}}$

(vi) $\left(\frac{x^{-4}}{y^{-10}}\right)^{\frac{5}{4}}$

(vii) $\left(\frac{\sqrt{2}}{\sqrt{3}}\right)^{5}\left(\frac{6}{7}\right)^{2}$

Solution: (i) $\left(\sqrt{\left(x^{-3}\right)}\right)^{5}=\left(\sqrt{\frac{1}{x^{3}}}\right)^{5}$

$\left(\frac{1}{x^{\frac{3}{2}}}\right)^{5}=\frac{1}{x^{\frac{15}{2}}}$

(ii) $\sqrt{x^{3} y^{-2}}=\frac{x^{\frac{3}{2}}}{y^{2 \times \frac{1}{2}}}=\frac{x^{\frac{3}{2}}}{y}$

(iii) $\left(x^{-\frac{2}{3}} y^{-\frac{1}{2}}\right)^{2}$

$=\left(x^{-\frac{2}{3}} y^{-\frac{1}{2}}\right)^{2}=\left(\frac{1}{x^{\frac{2}{3}} y^{\frac{1}{2}}}\right)^{2}$

$=\left(\frac{1}{x^{\frac{2}{3} \times 2} y^{\frac{1}{2} \times 2}}\right)$

$=\frac{1}{x^{\frac{4}{3}} y}$

(iv) $(\sqrt{x})^{-\frac{2}{3}} \sqrt{y^{4}} \div \sqrt{x y^{-\frac{1}{2}}}$

$=\left(x^{\frac{1}{2}}\right)^{-\frac{2}{3}}\left(y^{2}\right) \div \sqrt{x y^{-\frac{1}{2}}}$

$=\frac{x^{-\frac{1}{3}} y^{2}}{x^{\frac{1}{2}} y^{-\frac{1}{2} \times \frac{1}{2}}}$

$=\left(x^{-\frac{1}{3}} \times x^{-\frac{1}{2}}\right) \times\left(y^{2} \times y^{\frac{1}{4}}\right)$

$=\left(x^{-\frac{1}{3}-\frac{1}{2}}\right)\left(y^{2+\frac{1}{4}}\right)$

$=\left(x^{\frac{-2-3}{6}}\right)\left(y^{\frac{8+1}{4}}\right)$

$=\left(x^{-\frac{5}{6}}\right)\left(y^{\frac{9}{4}}\right)$

$=\frac{y^{\frac{9}{4}}}{x^{\frac{5}{6}}}$

(v) $\sqrt[5]{243 x^{10} y^{5} z^{10}}$

$=\left(243 x^{10} y^{5} z^{10}\right)^{\frac{1}{5}}$

$=(243)^{\frac{1}{5}} x^{\frac{10}{5}} y^{\frac{5}{5}} z^{\frac{10}{5}}$

$=\left(3^{5}\right)^{\frac{1}{5}} x^{2} y z^{2}$

$=3 x^{2} y z^{2}$

$(\mathrm{Vi})\left(\frac{x^{-4}}{y^{-10}}\right)^{\frac{5}{4}}$

$=\left(\frac{y^{10}}{x^{4}}\right)^{\frac{5}{4}}$

$=\left(\frac{y^{10 \times \frac{5}{4}}}{x^{4 \times \frac{5}{4}}}\right)$

$=\left(\frac{y^{\frac{25}{2}}}{x^{5}}\right)$

(vii) $\left(\frac{\sqrt{2}}{\sqrt{3}}\right)^{5}\left(\frac{6}{7}\right)^{2}$

$=\left(\sqrt{\frac{2}{3}}\right)^{5}\left(\frac{6}{7}\right)^{\frac{4}{2}}$

$=\left(\frac{2}{3}\right)^{\frac{5}{2}}\left(\frac{6}{7}\right)^{\frac{4}{2}}$

$=\left(\frac{2^{5}}{3^{5}}\right)^{\frac{1}{2}}\left(\frac{6^{4}}{7^{4}}\right)^{\frac{1}{2}}$

$=\left(\frac{2^{5}}{3^{5}} \times \frac{6^{4}}{7^{4}}\right)^{\frac{1}{2}}$

$=\left(\frac{2 \times 2 \times 2 \times 2 \times 2}{3 \times 3 \times 3 \times 3 \times 3} \times \frac{6 \times 6 \times 6 \times 6}{7 \times 7 \times 7 \times 7}\right)$

$=\left(\frac{512}{7203}\right)^{\frac{1}{2}}$

Question 2: Simplify

(i) $\left(16^{-1 / 5}\right)^{5 / 2}$

(ii) $\sqrt[5]{(32)^{-3}}$

(iii) $\sqrt[3]{(343)^{-2}}$

(iv) $(0.001)^{1 / 3}$

(v) $\frac{(25)^{3 / 2} \times(243)^{3 / 5}}{(16)^{5 / 4} \times(8)^{4 / 3}}$

(vi) $\left(\frac{\sqrt{2}}{5}\right)^{8} \div\left(\frac{\sqrt{2}}{5}\right)^{13}$

(vii) $\left(\frac{5^{-1} \times 7^{2}}{5^{2} \times 7^{-4}}\right)^{\frac{7}{2}} \times\left(\frac{5^{-2} \times 7^{3}}{5^{3} \times 7^{-5}}\right)^{\frac{-5}{2}}$

Solution: (i) $\left(16^{-\frac{1}{5}}\right)^{\frac{5}{2}}$

$=(16)^{-\frac{1}{5} \times \frac{5}{2}}=(16)^{-\frac{1}{2}}$

$=\left(4^{2}\right)^{-\frac{1}{2}}$

$=\left(4^{2 \times-\frac{1}{2}}\right)=\frac{1}{4}$

(ii) $\sqrt[5]{(32)^{-3}}$

$=\left[\left(2^{5}\right)^{-3}\right]^{\frac{1}{5}}$

$=\left(2^{-15}\right)^{\frac{1}{5}}$

$=2^{-3}$

$=\frac{1}{2^{3}}$

$=\frac{1}{8}$

(iii) $\sqrt[3]{(343)^{-2}}$

$=\left[(343)^{-2}\right]^{\frac{1}{3}}$

$=(343)^{-2 \times \frac{1}{3}}$

$=\left(7^{3}\right)^{-\frac{2}{3}}$

$=\left(7^{-2}\right)$

$=\left(\frac{1}{7^{2}}\right)$

$=\left(\frac{1}{49}\right)$

(iv) $(0.001)^{\frac{1}{3}}$

$=\left(\frac{1}{10^{3}}\right)^{\frac{1}{3}}=\frac{1}{10^{3 \times \frac{1}{3}}}$

$=\frac{1}{10}=0.1$

(v) $\frac{(25)^{\frac{3}{2}} \times(243)^{\frac{3}{5}}}{(16)^{\frac{5}{4}} \times(8)^{\frac{4}{3}}}$

$=\frac{\left(\left(5^{2}\right)\right)^{\frac{3}{2}} \times\left(\left(3^{5}\right)\right)^{\frac{3}{5}}}{\left(\left(4^{2}\right)\right)^{\frac{5}{4}} \times\left(\left(4^{2}\right)\right)^{\frac{4}{3}}}$

$=\frac{5^{3} \times 3^{3}}{2^{5} \times 2^{4}}$

$=\frac{125 \times 27}{32 \times 16}$

$=\frac{3375}{512}$

(vi) $\left(\frac{\sqrt{2}}{5}\right)^{8} \div\left(\frac{\sqrt{2}}{5}\right)^{13}=\left(\frac{\sqrt{2}}{5}\right)^{8-13}$

$=\left(\frac{\sqrt{2}}{5}\right)^{-5}=\frac{5^{5}}{2^{\frac{5}{2}}}=\frac{3125}{4 \sqrt{2}}$

(vii) $\left(\frac{5^{-1} \times 7^{2}}{5^{2} \times 7^{-4}}\right)^{\frac{7}{2}} \times\left(\frac{5^{-2} \times 7^{3}}{5^{3} \times 7^{-5}}\right)^{\frac{-5}{2}}$

$=\frac{5^{-1 \times \frac{7}{2}} \times 7^{2 \times \frac{7}{2}}}{5^{2 \times \frac{7}{2}} \times 7^{-4 \times \frac{7}{2}}} \times \frac{5^{-2 \times\left(\frac{-5}{2}\right)} \times 7^{3 \times\left(\frac{-5}{2}\right)}}{5^{3 \times\left(\frac{-5}{2}\right)} \times 7^{-5 \times\left(\frac{-5}{2}\right)}}$

$=\frac{5^{\frac{-7}{2}} \times 7^{7}}{5^{7} \times 7^{-14}}=\frac{5^{5} \times 7^{\frac{-15}{2}}}{5^{\frac{-15}{2}} \times 7^{\frac{25}{2}}}$

$=5^{\frac{-7}{2}+5-7+\frac{15}{2}} \times 7^{7-\frac{15}{2}+14-\frac{25}{2}}$

$=5^{\frac{25}{2}}-\frac{21}{2} \times 7^{21-\frac{40}{2}}=5^{\frac{4}{2}} \times 7^{\frac{2}{2}}$

$=5^{2} \times 7^{1}=25 \times 7=175$

Question 3: Prove that

(i) $\left(\sqrt{3 \times 5^{-3}} \div \sqrt[3]{3^{-1}} \sqrt{5}\right) \times \sqrt[6]{3 \times 5^{6}}=\frac{3}{5}$

(ii) $9^{\frac{3}{2}}-3 \times 5^{0}-\left(\frac{1}{81}\right)^{-\frac{1}{2}}=15$

(iii) $\left(\frac{1}{4}\right)^{-2}-3 \times 8^{\frac{2}{3}} \times 4^{0}+\left(\frac{9}{16}\right)^{-\frac{1}{2}}=\frac{16}{3}$

(iv) $\frac{2^{\frac{1}{2}} \times 3^{\frac{1}{3}} \times 4^{\frac{1}{4}}}{10^{-\frac{1}{5}} \times 5^{\frac{3}{5}}} \div \frac{3^{\frac{4}{3}} \times 5^{-\frac{7}{5}}}{4^{-\frac{3}{5}} \times 6}=10$

(v) $\sqrt{\frac{1}{4}}+(0.01)^{-\frac{1}{2}}-(27)^{\frac{2}{3}}=\frac{3}{2}$

(vi) $\frac{2^{n}+2^{n-1}}{2^{n+1}-2^{n}}=\frac{3}{2}$

(vii) $\left(\frac{64}{125}\right)^{-\frac{2}{3}}+\frac{1}{\left(\frac{256}{625}\right)^{\frac{1}{4}}}+\left(\frac{\sqrt{25}}{\sqrt[3]{64}}\right)^{0}=\frac{61}{16}$

(viii) $\frac{3^{-3} \times 6^{2} \times \sqrt{98}}{5^{2} \times \sqrt[3]{\frac{1}{25}} \times(15)^{-\frac{4}{3}} \times 3^{\frac{1}{3}}}=28 \sqrt{2}$

(ix) $\frac{(0.6)^{0}-(0.1)^{-1}}{\left(\frac{3}{8}\right)^{-1}\left(\frac{3}{2}\right)^{3}+\left(\frac{1}{3}\right)^{-1}}=\frac{-3}{2}$

Solution: (i) L.H.S.

$\left(\sqrt{3 \times 5^{-3}} \div \sqrt[3]{3^{-1}} \sqrt{5}\right) \times \sqrt[6]{3 \times 5^{6}}$

$=\left(\left(3 \times 5^{-3}\right)^{\frac{1}{2}} \div\left(3^{-1}\right)^{\frac{1}{3}}(5)^{\frac{1}{2}}\right)$

$\times\left(3 \times 5^{6}\right)^{\frac{1}{6}}$

$=\left((3)^{\frac{1}{2}}\left(5^{-3}\right)^{\frac{1}{2}} \div\left(3^{-1}\right)^{\frac{1}{3}}(5)^{\frac{1}{2}}\right)$

$\times\left(3 \times 5^{6}\right)^{\frac{1}{6}}$

$=\left((3)^{\frac{1}{2}}(5)^{\frac{-3}{2}} \div(3)^{\frac{-1}{3}}(5)^{\frac{1}{2}}\right)$

$\times\left((3)^{\frac{1}{6}} \times(5)^{\frac{6}{6}}\right)$

$=\left((3)^{\frac{1}{2}-\left(-\frac{1}{3}\right)} \times(5)^{-\frac{3}{2}-\frac{1}{2}}\right)$

$\times\left((3)^{\frac{1}{6}} \times(5)\right)$

$=\left((3)^{\frac{3+2}{6}} \times(5)^{-\frac{4}{2}}\right)$

$\times\left((3)^{\frac{1}{6}} \times(5)\right)$

$=\left((3)^{\frac{5}{6}} \times(5)^{-2}\right)$

$\times\left((3)^{\frac{1}{6}} \times(5)\right)$

$=\left((3)^{\frac{5}{6}+\frac{1}{6}} \times(5)^{-2+1}\right)$

$=\left((3)^{\frac{6}{6}} \times(5)^{-1}\right)$

$=\left((3)^{1} \times(5)^{-1}\right)$

$=\left((3) \times(5)^{-1}\right)$

$=\left((3) \times\left(\frac{1}{5}\right)\right)$

$=\left(\frac{3}{5}\right)$

= R.H.S.

(ii) $9^{\frac{3}{2}}-3 \times 5^{0}-\left(\frac{1}{81}\right)^{-\frac{1}{2}}$

$=\left(3^{2}\right)^{\frac{3}{2}}-3-\left(\frac{1}{9^{2}}\right)^{-\frac{1}{2}}$

$=3^{2 \times \frac{3}{2}}-3-\left(9^{-2}\right)^{-\frac{1}{2}}$

$=3^{3}-3-(9)^{-2 \times-\frac{1}{2}}$

$=27-3-9$

$=15$

(iii) $\left(\frac{1}{4}\right)^{-2}-3 \times 8^{\frac{2}{3}} \times 4^{0}+\left(\frac{9}{16}\right)^{-\frac{1}{2}}$

$=\left(\frac{1}{2^{2}}\right)^{-2}-3 \times 8^{\frac{2}{3}} \times 1+\left(\frac{3^{2}}{4^{2}}\right)^{-\frac{1}{2}}$

$=2^{4}-3 \times 2^{3 \times \frac{2}{3}}+\frac{4}{3}$

$=16-3 \times 4+\frac{4}{3}$

$=\frac{12+4}{3}$

$=\frac{16}{3}$

(iv) $\frac{2^{\frac{1}{2}} \times 3^{\frac{1}{3}} \times 4^{\frac{1}{4}}}{10^{-\frac{1}{5}} \times 5^{\frac{3}{5}}} \div \frac{3^{\frac{4}{3}} \times 5^{-\frac{7}{5}}}{4^{-\frac{3}{5}} \times 6}$

$=\frac{2^{\frac{1}{2}} \times 3^{\frac{1}{3}} \times\left(2^{2}\right)^{\frac{1}{4}}\left(2^{2}\right)^{-\frac{3}{5}} \times(2 \times 3)}{(2 \times 5)^{-\frac{1}{5}} \times 5^{\frac{3}{5}} \times 3^{\frac{4}{3}} \times 5^{-\frac{7}{5}}}$

$=\frac{2^{\frac{1}{2}} \times 2^{\frac{1}{2}} \times\left(2^{2}\right)^{-\frac{6}{5}} \times 2^{1} \times 3^{\frac{1}{3}} \times 3}{2^{-\frac{1}{5}} \times 5^{-\frac{1}{5}} \times 5^{\frac{3}{5}} \times 3^{\frac{4}{3}} \times 5^{-\frac{7}{5}}}$

$=\frac{2^{\frac{1}{5}} \times 2^{\frac{1}{2}} \times 2^{\frac{1}{2}} \times 2^{-\frac{6}{5}} \times 2 \times 3^{\frac{1}{3}} \times 3 \times 3^{-\frac{4}{3}}}{5^{-\frac{1}{5}} \times 5^{\frac{3}{5}} \times 5^{-\frac{7}{5}}}$

$=\frac{(2)^{\frac{1}{2}+\frac{1}{2}-\frac{6}{5}+1+\frac{1}{5}} \times(3)^{\frac{1}{3}+1-\frac{4}{3}}}{5^{-\frac{1}{5}} \times 5^{\frac{3}{5}} \times 5^{-\frac{7}{5}}}$

$=\frac{(2)^{\frac{1}{5}+2-\frac{6}{5}} \times(3)^{1-1}}{5^{-1}}$

$=\frac{(2)^{1} \times(3)^{0}}{5^{-1}}$

$=2 \times 1 \times 5$

$=10$

(v) $\sqrt{\frac{1}{4}}+(0.01)^{-\frac{1}{2}}-(27)^{\frac{2}{3}}$

$=\frac{1}{2}+\frac{1}{(0.01)^{\frac{1}{2}}}-\left(3^{3}\right)^{\frac{2}{3}}$

$=\frac{1}{2}+\frac{1}{(0.1)^{2 \times \frac{1}{2}}}-(3)^{3 \times \frac{2}{3}}$

$=\frac{1}{2}+\frac{1}{(0.1)^{1}}-(3)^{2}$

$=\frac{1}{2}+\frac{1}{(0.1)}-9$

$=\frac{3}{2}$

(vi) $\frac{2^{n}+2^{n-1}}{2^{n+1}-2^{n}}$

$=\frac{2^{n}+2^{n} \times 2^{-1}}{2^{n} \times 2^{1}-2^{n}}$

$=\frac{2^{n}\left[1+2^{-1}\right]}{2^{n}[2-1]}$

$=1+\frac{1}{2}$

$=\frac{3}{2}$

(vii) $\left(\frac{64}{125}\right)^{-\frac{2}{3}}+\frac{1}{\left(\frac{256}{625}\right)^{\frac{1}{4}}}+\left(\frac{\sqrt{25}}{\sqrt[3]{64}}\right)^{0}$

$=\left(\frac{125}{64}\right)^{\frac{2}{3}}+\frac{1}{\left(\frac{4^{4}}{5^{4}}\right)^{\frac{1}{4}}}+1$

$=\left(\frac{5^{3}}{4^{3}}\right)^{\frac{2}{3}}+\frac{1}{\left(\frac{4}{5}\right)}+1$

$=\left(\frac{5}{4}\right)^{2}+\frac{5}{4}+1$

$=\frac{25}{16}+\frac{9}{4}$

$=\frac{25}{16}+\frac{36}{16}$

$=\frac{61}{16}$

(viii) $\frac{3^{-3} \times 6^{2} \times \sqrt{98}}{5^{2} \times \sqrt[3]{\frac{1}{25}} \times(15)^{-\frac{1}{3}} \times 3^{\frac{1}{3}}}$

$=\frac{3^{-3} \times 36 \times \sqrt{7 \times 7 \times 2}}{5^{2} \times\left(\frac{1}{25}\right)^{\frac{1}{3}} \times(15)^{-\frac{4}{3}} \times 3^{\frac{1}{3}}}$

$=\frac{3^{-3} \times 2^{2} \times 3^{2} \times 2^{\frac{1}{2}} \times\left(7^{2}\right)^{\frac{1}{2}}}{5^{2} \times\left(5^{2}\right)^{\frac{-1}{3}} \times 3^{\frac{-4}{3}} \times 5^{\frac{-4}{3}} \times 3^{\frac{1}{3}}}$

$=2^{2} \cdot 2^{\frac{1}{2}} \cdot 3^{-3+2+\frac{4}{3}-\frac{1}{3}} \cdot 5^{\frac{2}{3}-2+\frac{4}{3}} \cdot 7^{1}$

$=4 \sqrt{2} \times 3^{0 \times} 5^{0} \times 7^{1}$

$=4 \sqrt{2} \times 1 \times 1 \times 7$

$=28 \sqrt{2}$

(ix) $\frac{(0.6)^{0}-(0.1)^{-1}}{\left(\frac{3}{8}\right)^{-1}\left(\frac{3}{2}\right)^{3}+\left(\frac{1}{3}\right)^{-1}}$

$=\frac{1-\frac{1}{0.1}}{\frac{8}{3} \times\left(\frac{3}{2}\right)^{3}-3}$

$=\frac{1-10}{\frac{8}{3} \times \frac{3^{3}}{2^{3}}-3}$

$=\frac{-9}{3^{2}-3}$

$=-3 / 2$

Question $4 .$ Show that:





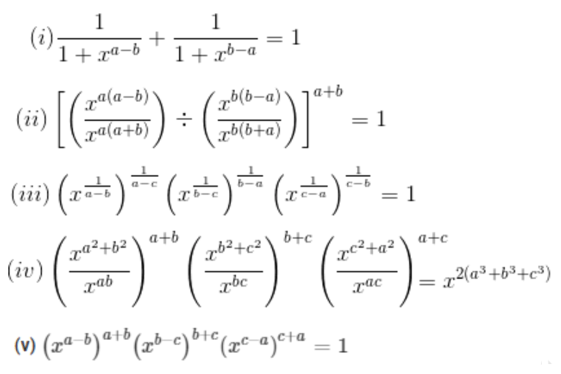
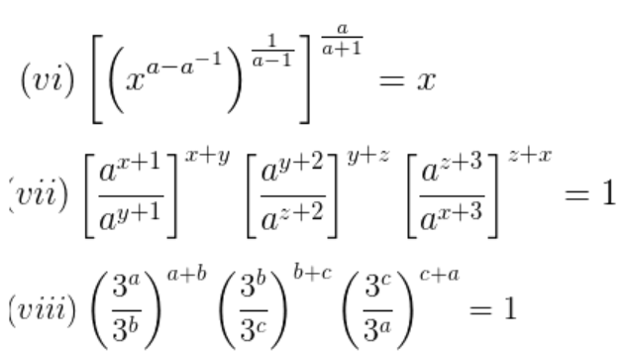
Solution: (i) $\frac{1}{1+x^{a-b}}+\frac{1}{1+x^{b-a}}$

$=\frac{1}{1+\frac{x^{a}}{x^{b}}}+\frac{1}{1+\frac{x^{b}}{x^{a}}}$

$=\frac{x^{b}}{x^{b}+x^{a}}+\frac{x^{a}}{x^{a}+x^{b}}$

$=\frac{x^{b}+x^{a}}{x^{a}+x^{b}}$

$=1$

$(i i)\left[\left(\frac{x^{a(a-b)}}{x^{a(a+b)}}\right) \div\left(\frac{x^{b(b-a)}}{x^{b(b+a)}}\right)\right]^{a+b}$

$=\left[\left(\frac{x^{a^{2}-a b}}{x^{a^{2}+a b}}\right) \div\left(\frac{x^{b^{2}-a b}}{x^{b^{2}+a b}}\right)\right]^{a+b}$

$=\left[x^{\left(a^{2}-a b\right)-\left(a^{2}-a b\right)}\right.$

$\left.\div x^{\left(b^{2}-a b\right)-\left(b^{2}-a b\right)}\right]^{a+b}$

$=\left[x^{-2 a b-(-2 a b)}\right]^{a+b}$

$=\left[x^{0}\right]^{a+b}=[1]^{a+b}=1$

$($ iii $)\left(x^{\frac{1}{a-b}}\right)^{\frac{1}{a-c}}\left(x^{\frac{1}{b-c}}\right)^{\frac{1}{b-a}}\left(x^{\frac{1}{c-a}}\right)^{\frac{1}{c-b}}$

$=\left(x^{\frac{1}{(a-b)(a-c)}}\right)\left(x^{\frac{1}{(b-c)(b-a)}}\right)\left(x^{\frac{1}{(c-a)(c-b)}}\right)$

$=x^{\left(\frac{1}{(a-b)(a-c)}+\frac{-1}{(b-c)(a-b)}+\frac{1}{(a-c)(b-c)}\right)}$

$=x^{\left(\frac{b-c-a+c+a-b}{(a-b)(a-c)(b-c)}\right)}$

$=x^{0}=1$

$(i v)\left(\frac{x^{a^{2}+b^{2}}}{x^{a b}}\right)^{a+b}$

$\left(\frac{x^{b^{2}+c^{2}}}{x^{b c}}\right)^{b+c}$

$\left(\frac{x^{c^{2}+a^{2}}}{x^{a c}}\right)^{a+c}$

$=\left(x^{a^{2}+b^{2}-a b}\right)^{a+b}$

$\left(x^{b^{2}+c^{2}-b c}\right)^{b+c}$

$\left(x^{c^{2}+a^{2}-a c}\right)^{a+c}$

$=\left(x^{a+b\left(a^{2}+b^{2}-a b\right)}\right)$

$\left(x^{b+c\left(b^{2}+c^{2}-b c\right)}\right)$

$\left(x^{a+c\left(c^{2}+a^{2}-a c\right)}\right)$

$=\left(x^{a^{3}+a b^{2}-a^{2} b+a b^{2}+b^{3}-a b^{2}}\right)$

$\left(x^{b^{3}+b c^{2}-b^{2} c+c b^{2}+c^{3}-b c^{2}}\right)$

$\left(x^{a c^{2}+a^{3}-a^{2} c+c^{3}+a^{2} c-a c^{2}}\right)$

$=\left(x^{a^{3}+b^{3}}\right)\left(x^{b^{3}+c^{3}}\right)\left(x^{a^{3}+c^{3}}\right)$

$=\left(x^{a^{3}+b^{3}+b^{3}+c^{3}+a^{3}+c^{3}}\right)$

$=\left(x^{2 a^{3}+2 b^{3}+2 c^{3}}\right)$

(v) $\left(x^{a-b}\right)^{a+b}\left(x^{b-c}\right)^{b+c}\left(x^{c-a}\right)^{c+a}=1$

$\left(x^{a-b}\right)^{a+b}\left(x^{b-c}\right)^{b+c}\left(x^{c-a}\right)^{c+a}$

$=x^{a^{2}-b^{2}} x^{b^{2}-c^{2}} x^{c^{2}-a^{2}}$

$=x^{a^{2}-b^{2}+b^{2}-c^{2}+c^{2}-a^{2}}$

$=x^{0}$

$=1$

$(v i)$ $\left[\left(x^{a-a^{-1}}\right)^{\frac{1}{a-1}}\right]^{\frac{a}{a+1}}$

$=\left[\left(x^{\frac{a-a^{-1}}{a-1}}\right)\right]^{\frac{a}{a+1}}$

$=\left(x^{\frac{a\left(a-a^{-1}\right)}{a^{2}-1}}\right)$

$=\left(x^{\frac{a^{2}-a^{-1+1}}{a^{2}-1}}\right)$

$=\left(x^{\frac{a^{2}-1}{a^{2}-1}}\right)$

$=x^{1}=x$

$(v i i)\left[\frac{a^{x+1}}{a^{y+1}}\right]^{x+y}$

$\left[\frac{a^{y+2}}{a^{z+2}}\right]^{y+z}$

$\left[\frac{a^{z+3}}{a^{x+3}}\right]^{z+x}$

$=\left[a^{(x+1)-(y+1)}\right]^{x+y}$

$\left[a^{(y+2)-(z+2)}\right]^{y+z}$

$\left[a^{(z+3)-(x+3)}\right]^{z+x}$

$=\left[a^{x-y}\right]^{x+y}$

$\left[a^{y-z}\right]^{y+z}$

$\left[a^{\tilde{z}-x}\right]^{\tilde{z}+x}$

$=\left[a^{x^{2}-y^{2}}\right]$

$\left[a^{y^{2}-z^{2}}\right]$

$\left[a^{z^{2}-x^{2}}\right]$

$=a^{x^{2}-y^{2}+y^{2}-z^{2}+z^{2}-x^{2}}$

$=a^{0}=1$

$(v i i i)\left(\frac{3^{a}}{3^{b}}\right)^{a+b}$

$\left(\frac{3^{b}}{3^{c}}\right)^{b+c}$

$\left(\frac{3^{c}}{3^{a}}\right)^{c+a}$

$=\left(3^{a-b}\right)^{a+b}$

$\left(3^{b-c}\right)^{b+c}$

$\left(3^{c-a}\right)^{c+a}$

$=3^{a^{2}-b^{2}} \times 3^{b^{2}-c^{2}} \times 3^{c^{2}-a^{2}}$

$=3^{a^{2}-b^{2}+b^{2}-c^{2}+c^{2}-a^{2}}$

$=3^{0}=1$

Exercise-VSAQs

Question 1: Write (625) ${ }^{-14}$ in decimal form.

Solution: $(625)^{-1 / 4}=\left(5^{4}\right)^{-14}=5^{-1}=1 / 5=0.2$

Question 2: State the product law of exponents:

Solution: To multiply two parts having same base, add the exponents.

Mathematically: $\mathrm{x}^{\mathrm{m}} \times \mathrm{x}^{\mathrm{n}}=\mathrm{x}^{\mathrm{m}+n}$

Question 3: State the quotient law of exponents.

Solution: To divide two exponents with the same base, subtract the powers.

Mathematically: $x^{m} \div x^{n}=x^{m-n}$

Question 4: State the power law of exponents.

Solution: Power law of exponents :

$\left(\mathrm{X}^{\mathrm{m}}\right)^{\mathrm{n}}=\mathrm{X}^{\mathrm{m} \times \mathrm{n}}=\mathrm{X}^{\mathrm{mn}}$

Question 5: For any positive real number $\mathrm{x}$, find the value of

$\left(\frac{x^{a}}{x^{b}}\right)^{a+b}\left(\frac{x^{b}}{x^{c}}\right)^{b+c}\left(\frac{x^{c}}{x^{a}}\right)^{c+a}$

Solution: $\left(\frac{x^{a}}{x^{b}}\right)^{a+b}$

$\left(\frac{x^{b}}{x^{c}}\right)^{b+c}$

$\left(\frac{x^{c}}{x^{a}}\right)^{c+a}$

$=\left(x^{a-b}\right)^{a+b} \times\left(x^{b-c}\right)^{b+c}$

$\times\left(x^{c-a}\right)^{c+a}$

$=x^{a^{2}-b^{2}} \times x^{b^{2}-c^{2}}$

$\times x^{c^{2}-a^{2}}$

$=x^{a^{2}-b^{2}+b^{2}-c^{2}+c^{2}-a^{2}}$

$=1$

Question $6:$ Write the value of $\left\{5\left(8^{1 / 3}+27^{1 / 3}\right)^{3}\right\}^{1 / 4}$

Solution: $\left\{5\left(8^{1 / 3}+27^{1 / 3}\right)^{3}\right\}^{1 / 4}$

$=\left\{5\left(2^{3 \times 1 / 3}+3^{3 \times 1 / 3}\right)^{3}\right\}^{1 / 4}$

$=\left\{5(2+3)^{\wedge} 3\right\}^{1 / 4}$

$=\left(5^{4}\right)^{1 / 4}$

$=5$

Also Read,

Download NCERT Class 9 Maths Chapterwise Book Free

Download NCERT Class 10 Maths Chapterwise Book Free

Download NCERT Class 9 Maths Chapterwise Exemplar Free

Download NCERT Class 10 Maths Chapterwise Exemplar Free

If you have any Confusion related to RD Sharma Solutions for Class 9 Maths Chapter 2 Exponents of Real Numbers then feel free to ask in the comments section down below.

To watch Free Learning Videos on Class 9 by Kota’s top Faculties Install the eSaral App