RD Sharma Solutions for Class 9 Maths Chapter 7 Introduction to Euclid's Geometry – Free PDF Download

Hey, are you a class 9 student and looking for ways to download RD Sharma Solutions for Class 9 Maths Chapter 7 "Introduction to Euclid's Geometry"? If yes. Then read this post till the end.

In this article, we have listed RD Sharma Solutions for Class 9 Maths Chapter 7 in PDF that is prepared by Kota’s top IITian’s Faculties by keeping Simplicity in mind.

If you want to learn and understand class 9 Maths Chapter 7 "Introduction to Euclid's Geometry" in an easy way then you can use these solutions PDF.

Chapter 7 of RD Sharma Class 9 deals with Euclid’s Geometry. Euclid's Geometry is a fundamental concept that forms the basis for much more advanced topics. If you want to improve your basic Euclid's Geometry, then you can use this.

RD Sharma Solutions helps students to Practice important concepts of subjects easily. RD Sharma class 9 solutions provide detailed explanations of all the  exercise questions that students can use to clear their doubts instantly.

If you want to become good at Math then it is very important for you to have a good knowledge of all the important topics of class 9 math, so to learn and practice those topics you can use eSaral RD Sharma Solutions.

In this article, we have listed RD Sharma Solutions for Class 9 Maths Chapter 7 that you can download to start your preparations anytime.

So, without wasting more time Let’s start.

RD Sharma Solutions for Class 9 Maths Chapter 7 Introduction to Euclid's Geometry - Free PDF Download

Question 1: Define the following terms.

(i) Line segment

(ii) Collinear points

(iii) Parallel lines

(iv) Intersecting lines

(v) Concurrent lines

(vi) Ray

(vii) Half-line

Solution: (i) Line segment: The part of a line that connects two points or we can say that a shortest distance between the two points. A line segment is one-dimensional.



Here $\mathrm{AB}$ is a line segment.

(ii) Collinear points: Two or more points are said to be collinear if all the points lie on same line.

(iii) Parallel lines : Two lines in a plane are said to be parallel lines if they do not intersect each other.



Here I and $\mathrm{m}$ are parallel lines.

(iv) Intersecting lines: Two lines are intersecting if they have a common point. The common point is known as point of intersection.



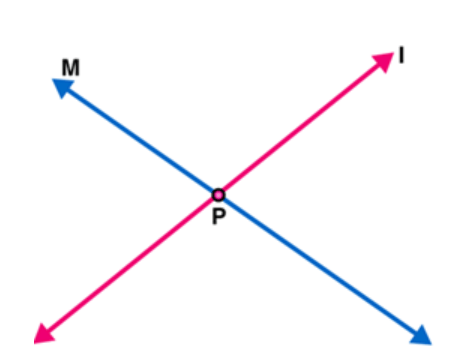
Here $I$ and $M$ are intersecting lines. And $P$ is point of intersection.

(v) Concurrent lines: Two or more lines are said to be concurrent if there is a point which lies on all of them.



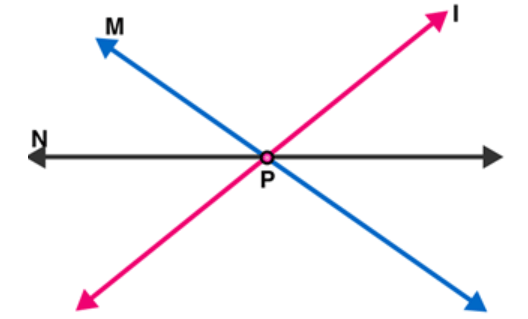
Here I, $\mathrm{m}$ and $\mathrm{n}$ are concurrent lines.

(vi) Ray: A straight line extending from a point indefinitely in one direction only.



Here $\mathrm{OA}$ is a ray.

(vii) Half-line: If $A$, B. C be the points on a line I, such that A lies between B and C, and we delete the point A from line I, the two parts of I that remain are each called a half-line.



Question 2: (i) How many lines can pass through a given point?

(ii) In how many points can two distinct lines at the most intersect?



Solution: (i) Infinitely many

(ii) One

Question 3: (i) Given two points $\mathrm{P}$ and $\mathrm{Q}$. Find how many line segments do they determine.

(ii) Name the line segments determined by the three collinear points $\mathrm{P}, \mathrm{Q}$ and $\mathrm{R}$.

Solution: (i) One

(ii) $\mathrm{PQ}, \mathrm{QR}, \mathrm{PR}$

Question 4: Write the truth value (T/F) of each of the following statements:

(i) Two lines intersect in a point.

(ii) Two lines may intersect in two points.

(iii) A segment has no length.

(iv) Two distinct points always determine a line.

(v) Every ray has a finite length.

(vi) A ray has one end-point only.

(vii) A segment has one end-point only.

(viii) The ray AB is same as ray BA.

(ix) Only a single line may pass through a given point.

(x) Two lines are coincident if they have only one point in common

Solution: (i) False

(ii) False

(iii) False

(iv) True

(v) False

(vi) True

(vii) False

(viii) False

(ix) False

(x) False

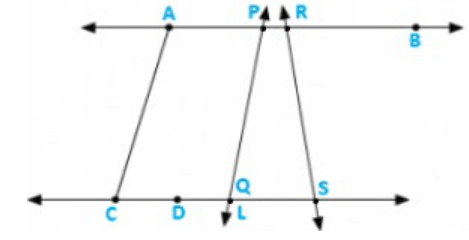
Question 5: In the below figure, name the following:

(i) Five line segments

(ii) Five rays

(iii) Four collinear points

(iv) Two pairs of non–intersecting line segments



Solution: (i) Five line segments $A B, C D, A C, P Q . D S$

(ii) Five rays :

$\overrightarrow{P A}, \overrightarrow{R B}, \overrightarrow{D C}, \overrightarrow{Q S}, \overrightarrow{D S}$

(iii) Four collinear points. C, D, Q, S

(iv) Two pairs of non-intersecting line segments $A B$ and $C D, P B$ and LS.

Question 6: Fill in the blanks so as to make the following statements true:

(i) Two distinct points in a plane determine a___________ line.

(ii) Two distinct _________in a plane cannot have more than one point in common.

(iii) Given a line and a point, not on the line, there is one and only _____________ line which passes through the given point and is _______________ to the given line.

(iv) A line separates a plane into _________ parts namely the __________ and the _____ itself.

Solution: (i) unique

(ii) lines

(iii) perpendicular, perpendicular

(iv) three, two half planes, line.

Exercise VSAQs Page No: $7.9$

Question 1: How many least number of distinct points determine a unique line?

Solution: Two

Question 2: How many lines can be drawn through both the given points?

Solution: One

Question 3: How many lines can be drawn through a given point?

Solution: Infinite

Question 4: In how many points two distinct lines can intersect?

Solution: One

Question 5: In how many points a line, not in a plane, can intersect the plane?

Solution: One

Question 6: In how many points two distinct planes can intersect?

Solution: Infinite

Also Read,

Download NCERT Class 9 Maths Chapterwise Book Free

Download NCERT Class 10 Maths Chapterwise Book Free

Download NCERT Class 9 Maths Chapterwise Exemplar Free

Download NCERT Class 10 Maths Chapterwise Exemplar Free

If you have any Confusion related to RD Sharma Solutions for Class 9 Maths Chapter 7 Introduction to Euclid's Geometry, then feel free to ask in the comments section down below.

To watch Free Learning Videos on Class 9 by Kota’s top Faculties Install the eSaral App