
RD Sharma Solutions for Class 9 Maths Chapter 8 Lines and Angles – Free PDF Download
Hey, are you a class 9 student and looking for ways to download RD Sharma Solutions for Class 9 Maths Chapter 8 "Lines and Angles"? If yes. Then read this post till the end.
In this article, we have listed RD Sharma Solutions for Class 9 Maths Chapter 8 in PDF that is prepared by Kota’s top IITian’s Faculties by keeping Simplicity in mind.
If you want to learn and understand class 9 Maths Chapter 8 "Lines and Angles" in an easy way then you can use these solutions PDF.
Chapter 8 of RD Sharma Class 9 deals with lines and angles, their different types and formulas. If you want to improve your basic lines and angles, then you can use this.
RD Sharma Solutions helps students to Practice important concepts of subjects easily. RD Sharma class 9 solutions provide detailed explanations of all the exercise questions that students can use to clear their doubts instantly.
If you want to become good at Math then it is very important for you to have a good knowledge of all the important topics of class 9 math, so to learn and practice those topics you can use eSaral RD Sharma Solutions.
In this article, we have listed RD Sharma Solutions for Class 9 Maths Chapter 8 that you can download to start your preparations anytime.
So, without wasting more time Let’s start.
RD Sharma Solutions for Class 9 Maths Chapter 8 Lines and Angles - Free PDF Download
Question 1: Write the complement of each of the following angles:
(i) $20^{\circ}$
(ii) $35^{\circ}$
(iii) $90^{\circ}$
(iv) $77^{\circ}$
$(v) 30^{\circ}$
Solution: (i) The sum of an angle and its complement $=90^{\circ}$
Therefore, the complement of $20^{\circ}=90^{\circ}-20^{\circ}=70^{\circ}$
(ii) The sum of an angle and its complement $=90^{\circ}$
Therefore, the complement of $35^{\circ}=90^{\circ}-35^{\circ}=55$
(iii) The sum of an angle and its complement $=90^{\circ}$
Therefore, the complement of $90^{\circ}=90^{\circ}-90^{\circ}=0^{\circ}$
(iv) The sum of an angle and its complement $=90^{\circ}$
Therefore, the complement of $77^{\circ}=90^{\circ}-77^{\circ}=13^{\circ}$
(v) The sum of an angle and its complement $=90^{\circ}$
Therefore, the complement of $30^{\circ}=90^{\circ}-30^{\circ}=60^{\circ}$
Question $2:$ Write the supplement of each of the following angles:
(i) $54^{\circ}$
(ii) $132^{\circ}$
(iii) $138^{\circ}$
Solution: (i) The sum of an angle and its supplement $=180^{\circ}$.
Therefore supplement of angle $54^{\circ}=180^{\circ}-54^{\circ}=126^{\circ}$
(ii) The sum of an angle and its supplement $=180^{\circ}$.
Therefore supplement of angle $132^{\circ}=180^{\circ}-132^{\circ}=48^{\circ}$
(iii) The sum of an angle and its supplement $=180^{\circ}$.
Therefore supplement of angle $138^{\circ}=180^{\circ}-138^{\circ}=42^{\circ}$
Question 3: If an angle is $28^{\circ}$ less than its complement, find its measure?
Solution: Let the measure of any angle is ' a 'degrees
Thus, its complement will be $(90-a)^{\circ}$
So, the required angle $=$ Complement of $a-28$
$a=(90-a)-28$
$2 \mathrm{a}=62$
$a=31$
Hence, the angle measured is $31^{\circ}$.
Question $4:$ If an angle is $30^{\circ}$ more than one half of its complement, find the measure of the angle?
Solution: Let an angle measured by ' $a$ ' in degrees
Thus, its complement will be $(90-\mathrm{a})^{\circ}$
Required Angle $=30^{\circ}+$ complement $/ 2$
$a=30^{\circ}+(90-a)^{\circ} / 2$
$a+a / 2=30^{\circ}+45^{\circ}$
$3 a / 2=75^{\circ}$
$\mathrm{a}=50^{\circ}$
Therefore, the measure of required angle is $50^{\circ}$.
Question 5 : Two supplementary angles are in the ratio $4: 5 .$ Find the angles?
Solution: Two supplementary angles are in the ratio $4: 5$.
Let us say, the angles are $4 \mathrm{a}$ and $5 \mathrm{a}$ (in degrees)
Since angle are supplementary angles;
Which implies, $4 \mathrm{a}+5 \mathrm{a}=180^{\circ}$
$9 a=180^{\circ}$
$a=20^{\circ}$
Therefore, $4 \mathrm{a}=4(20)=80^{\circ}$ and
$5(a)=5(20)=100^{\circ}$
Hence, required angles are $80^{\circ}$ and $100^{\circ}$.
Question 6 : Two supplementary angles differ by $48^{\circ} .$ Find the angles?
Solution: Given: Two supplementary angles differ by $48^{\circ}$.
Consider $a^{\circ}$ be one angle then its supplementary angle will be equal to $(180-a)^{\circ}$ According to the question;
$(180-a)-x=48$
$(180-48)=2 a$
132 = 2a
$132 / 2=a$
Or $a=66^{0}$
Therefore, $180-\mathrm{a}=114^{\circ}$
Question 7: An angle is equal to 8 times its complement. Determine its measure?
Solution: Given: Required angle $=8$ times of its complement
Consider $a^{0}$ be one angle then its complementary angle will be equal to $(90-a)^{\circ}$
According to the question;
$\mathrm{a}=8$ times of its complement
$a=8(90-a)$
$a=720-8 a$
$a+8 a=720$
$9 a=720$
$a=80$
Therefore, the required angle is $80^{\circ}$.
Exercise $8.2$
Question 1: In the below Fig. OA and OB are opposite rays:
(i) If $x=25^{\circ}$, what is the value of $y$ ?
(ii) If $y=35^{\circ}$, what is the value of $x ?$
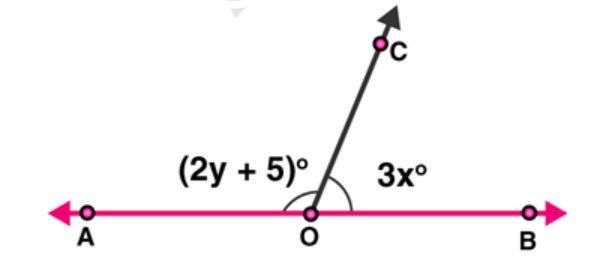
Solution: (i) Given: $x=25$
From figure: $\angle \mathrm{AOC}$ and $\angle \mathrm{BOC}$ form a linear pair
Which implies, $\angle A O C+\angle B O C=180^{\circ}$
From the figure, $\angle A O C=2 y+5$ and $\angle B O C=3 x$
$\angle A O C+\angle B O C=180^{\circ}$
$(2 y+5)+3 x=180$
$(2 y+5)+3(25)=180$
$2 y+5+75=180$
$2 y+80=180$
$2 \mathrm{y}=100$
$y=100 / 2=50$
Therefore, $y=50^{\circ}$
(ii) Given: $y=35^{\circ}$
From figure: $\angle A O C+\angle B O C=180^{\circ}$ (Linear pair angles)
$(2 y+5)+3 x=180$
$(2(35)+5)+3 x=180$
$75+3 x=180$
$3 x=105$
$x=35$
Therefore, $x=35^{\circ}$
Question 2: In the below figure, write all pairs of adjacent angles and all the linear pairs.
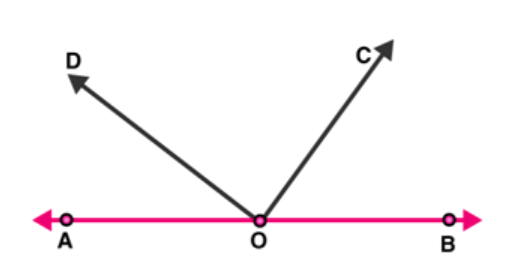
Solution: From figure, pairs of adjacent angles are :
$(\angle \mathrm{AOC}, \angle \mathrm{COB}) ;(\angle \mathrm{AOD}, \angle \mathrm{BOD}) ;(\angle \mathrm{AOD}, \angle \mathrm{COD}) ;(\angle \mathrm{BOC}, \angle \mathrm{COD})$
And Linear pair of angles are $(\angle A O D, \angle B O D)$ and $(\angle A O C, \angle B O C)$.
[As $\angle A O D+\angle B O D=180^{\circ}$ and $\left.\angle A O C+\angle B O C=180^{\circ} .\right]$
Question 3 : In the given figure, find $x$. Further find $\angle B O C, \angle C O D$ and $\angle A O D$.
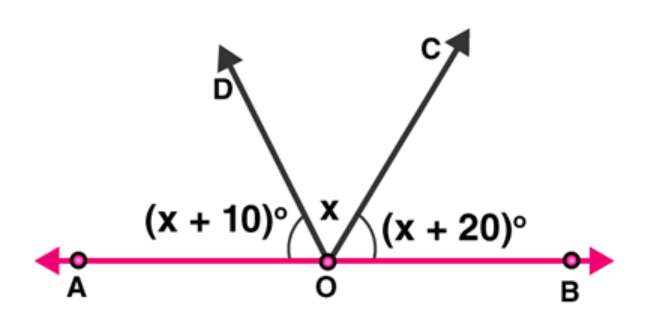
Solution: From figure, $\angle A O D$ and $\angle B O D$ form a linear pair,
Therefore, $\angle A O D+\angle B O D=180^{\circ}$
Also, $\angle A O D+\angle B O C+\angle C O D=180^{\circ}$
Given: $\angle A O D=(x+10)^{\circ}, \angle C O D$
$(x+10)+x+(x+20)=180$
$3 x+30=180$
$3 x=180-30$
$x=150 / 3$
$x=50^{\circ}$
Now,
$\angle A O D=(x+10)=50+10=60$
$\angle C O D=x=50$
$\angle B O C=(x+20)=50+20=70$
Hence, $\angle A O D=60^{\circ}, \angle C O D=50^{\circ}$ and $\angle B O C=70^{\circ}$
Question 4: In figure, rays OA, OB, OC, OD and OE have the common end point 0. Show that $\angle A O B+\angle B O C+\angle C O D+\angle D O E+\angle E O A=360^{\circ}$
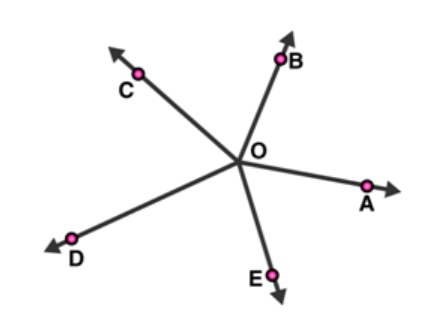
Solution:
Given: Rays $\mathrm{OA}, \mathrm{OB}, \mathrm{OC}, \mathrm{OD}$ and $\mathrm{OE}$ have the common endpoint $\mathrm{O}$.
Draw an opposite ray $O X$ to ray $O A$, which make a straight line $A X$.
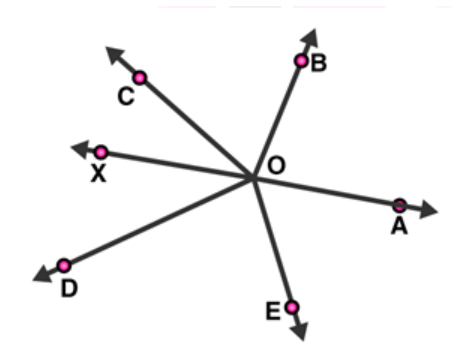
From figure:
$\angle A O B$ and $\angle B O X$ are linear pair angles, therefore,
$\angle A O B+\angle B O X=180^{\circ}$
Or, $\angle A O B+\angle B O C+\angle C O X=180^{\circ}$___________(1)
Also,
$\angle \mathrm{AOE}$ and $\angle \mathrm{EOX}$ are linear pair angles, therefore,
$\angle A O E+\angle E O X=180^{\circ}$
Or, $\angle A O E+\angle D O E+\angle D O X=180^{\circ}$__________(2)
By adding equations, (1) and (2), we get;
$\angle A O B+\angle B O C+\angle C O F+\angle A O E+\angle D O E+\angle D O X=180^{\circ}+180^{\circ}$
$\angle A O B+\angle B O C+\angle C O D+\angle D O E+\angle E O A=360^{\circ}$
Hence Proved.
Question 5 : In figure, $\angle A O C$ and $\angle B O C$ form a linear pair. If $a-2 b=30^{\circ}$, find $a$ and $b$ ?
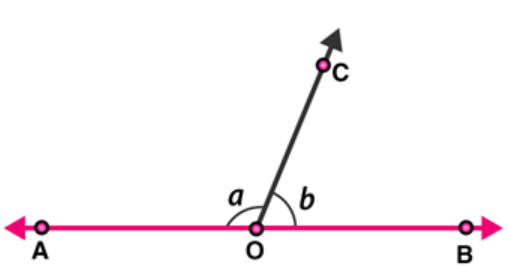
Solution:
Given : $\angle \mathrm{AOC}$ and $\angle \mathrm{BOC}$ form a linear pair.
$\Rightarrow a+b=180^{\circ} \ldots . .(1) $
$a-2 b=30^{\circ} \ldots$(2) (given)
On subtracting equation $(2)$ from $(1)$, we get
$a+b-a+2 b=180-30$
$3 b=150$
$b=150 / 3$
$b=50^{\circ}$
Since, $a-2 b=30^{\circ}$
$a-2(50)=30$
$a=30+100$
$a=130^{\circ}$
Therefore, the values of $a$ and $b$ are $130^{\circ}$ and $50^{\circ}$ respectively.
Question 6: How many pairs of adjacent angles are formed when two lines intersect at a point?
Solution: Four pairs of adjacent angles are formed when two lines intersect each other at a single point.
For example, Let two lines $A B$ and $C D$ intersect at point $O$.
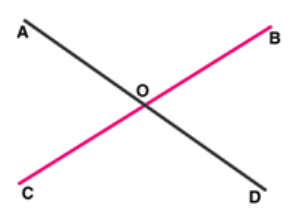
The 4 pair of adjacent angles are :
$(\angle A O D, \angle D O B),(\angle D O B, \angle B O C),(\angle C O A, \angle A O D)$ and $(\angle B O C, \angle C O A)$
Question 7: How many pairs of adjacent angles, in all, can you name in figure given?
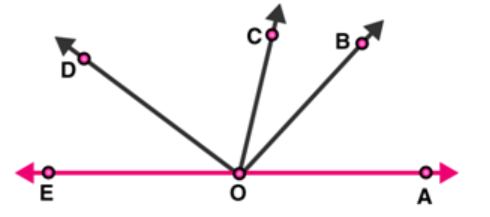
Solution: Number of Pairs of adjacent angles, from the figure, are :
$\angle \mathrm{EOC}$ and $\angle \mathrm{DOC}$
$\angle \mathrm{EOD}$ and $\angle \mathrm{DOB}$
$\angle \mathrm{DOC}$ and $\angle \mathrm{COB}$
$\angle \mathrm{EOD}$ and $\angle \mathrm{DOA}$
$\angle \mathrm{DOC}$ and $\angle \mathrm{COA}$
$\angle B O C$ and $\angle B O A$
$\angle B O A$ and $\angle B O D$
$\angle \mathrm{BOA}$ and $\angle \mathrm{BOE}$
$\angle \mathrm{EOC}$ and $\angle \mathrm{COA}$
$\angle \mathrm{EOC}$ and $\angle \mathrm{COB}$
Hence, there are 10 pairs of adjacent angles.
Question 8: In figure, determine the value of $x$.
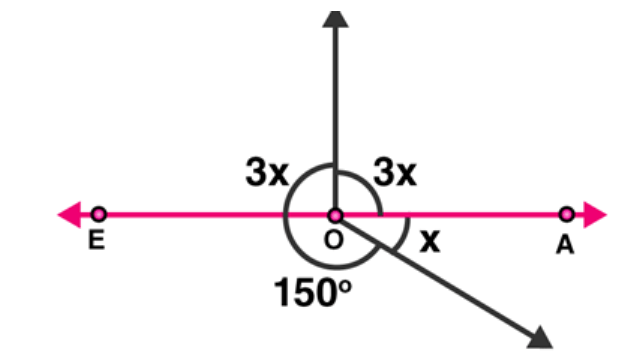
Solution: The sum of all the angles around a point $\mathrm{O}$ is equal to $360^{\circ}$.
Therefore,
$3 x+3 x+150+x=360^{\circ}$
$7 x=360^{\circ}-150^{\circ}$
$7 x=210^{\circ}$
$x=210 / 7$
$x=30^{\circ}$
Hence, the value of $x$ is $30^{\circ}$.
Question 9 : In figure, $A O C$ is a line, find $x$.
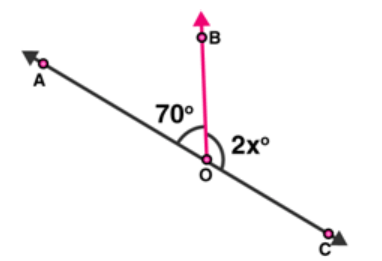
Solution: From the figure, $\angle A O B$ and $\angle B O C$ are linear pairs,
$\angle A O B+\angle B O C=180^{\circ}$
$70+2 x=180$
$2 x=180-70$
$2 x=110$
$x=110 / 2$
$x=55$
Therefore, the value of $x$ is $55^{\circ}$.
Question 10: In figure, POS is a line, find $x$.
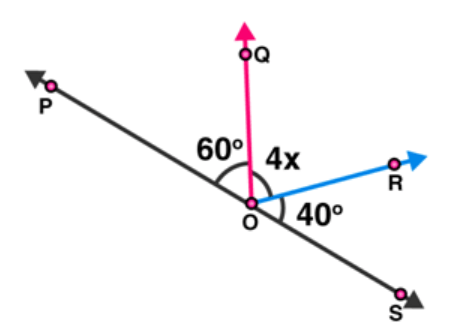
Solution: From figure, $\angle P O Q$ and $\angle Q O S$ are linear pairs.
Therefore,
$\angle \mathrm{POQ}+\angle \mathrm{QOS}=180^{\circ}$
$\angle \mathrm{POQ}+\angle \mathrm{QOR}+\angle \mathrm{SOR}=180^{\circ}$
$60^{\circ}+4 x+40^{\circ}=180^{\circ}$
$4 x=180^{\circ}-100^{\circ}$
$4 x=80^{\circ}$
$x=20^{\circ}$
Hence, the value of $\mathrm{x}$ is $20^{\circ}$.
Exercise 8.3
Question 1: In figure, lines $I_{1}$, and $I_{2}$ intersect at O, forming angles as shown in the figure. If $x$ $=45$. Find the values of $\mathbf{y}, \mathbf{z}$ and $\mathbf{u}$.
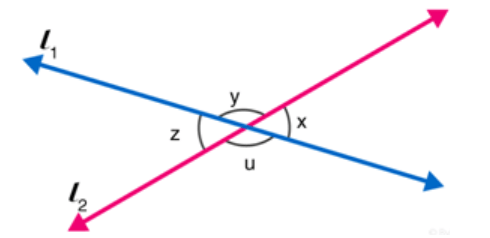
Solution: Given: $x=45^{\circ}$
Since vertically opposite angles are equal, therefore $z=x=45^{\circ}$
$z$ and $u$ are angles that are a linear pair, therefore, $z+u=180^{\circ}$
Solve, $z+u=180^{\circ}$, for $u$
$u=180^{\circ}-z$
$u=180^{\circ}-45$
$\mathrm{u}=135^{\circ}$
Again, $x$ and $y$ angles are a linear pair.
$x+y=180^{\circ}$
$y=180^{\circ}-x$
$y=180^{\circ}-45^{\circ}$
$y=135^{\circ}$
Hence, remaining angles are $y=135^{\circ}, \mathrm{u}=135^{\circ}$ and $\mathrm{z}=45^{\circ}$
Question 2: In figure, three coplanar lines intersect at a point O, forming angles as shown in the figure. Find the values of $\mathbf{x}, \mathbf{y}, \mathbf{z}$ and $\mathrm{u}$.
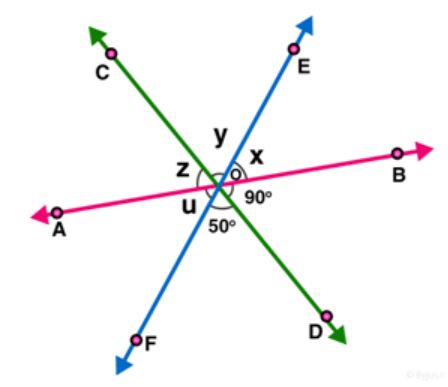
Solution: $(\angle B O D, z) ;(\angle D O F, y)$ are pair of vertically opposite angles.
So, $\angle B O D=z=90^{\circ}$
$\angle \mathrm{DOF}=\mathrm{y}=50^{\circ}$
[Vertically opposite angles are equal.]
Now, $x+y+z=180$ [Linear pair] [AB is a straight line]
$x+y+z=180$
$x+50+90=180$
$x=180-140$
$x=40$
Hence values of $x, y, z$ and $u$ are $40^{\circ}, 50^{\circ}, 90^{\circ}$ and $40^{\circ}$ respectively.
Question 3 : In figure, find the values of $\mathbf{x}, \mathbf{y}$ and $\mathbf{z}$
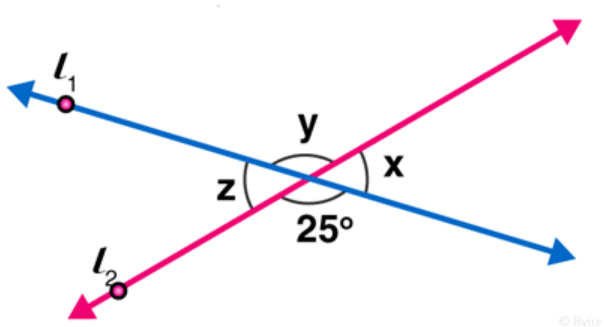
Solution: From figure,
$\mathrm{y}=25^{\circ}$ [Vertically opposite angles are equal]
Now $\angle x+\angle y=180^{\circ}$ [Linear pair of angles]
$x=180-25$
$x=155$
Also, $z=x=155$ [Vertically opposite angles]
Answer: $y=25^{\circ}$ and $z=155^{\circ}$
Question $4:$ In figure, find the value of $x$.
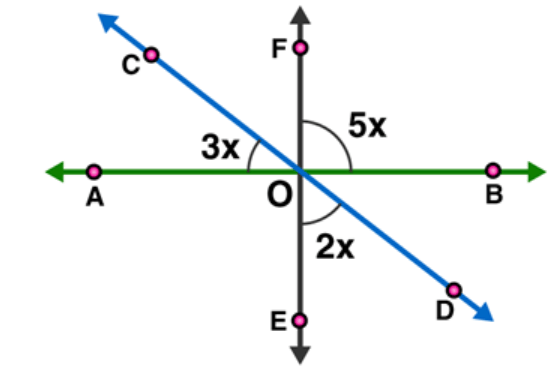
Solution: $\angle \mathrm{AOE}=\angle \mathrm{BOF}=5 \mathrm{x}[$ Vertically opposite angles $]$
$\angle \mathrm{COA}+\angle \mathrm{AOE}+\angle \mathrm{EOD}=180^{\circ}$ [Linear pair]
$3 x+5 x+2 x=180$
$10 \mathrm{x}=180$
$x=180 / 10$
$x=18$
The value of $x=18^{\circ}$
Question $5:$ Prove that bisectors of a pair of vertically opposite angles are in the same straight line.
Solution:
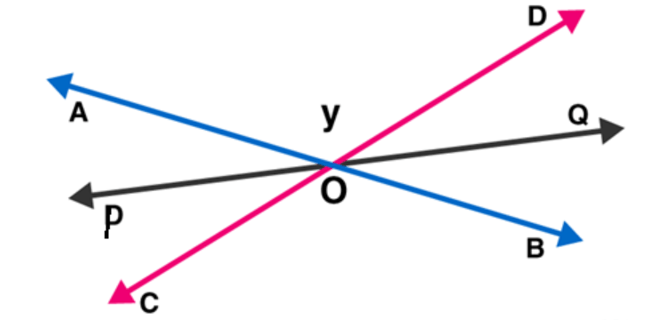
\text { Lines } A B \text { and } C D \text { intersect at point } O, \text { such that }
$\angle A O C=\angle B O D$ (vertically angles) $\ldots$(1)
Also OP is the bisector of $A O C$ and $O Q$ is the bisector of $B O D$
To Prove: $\mathrm{POQ}$ is a straight line.
OP is the bisector of $\angle A O C$ :
$\angle \mathrm{AOP}=\angle \mathrm{COP} \ldots$(2)
$\mathrm{OQ}$ is the bisector of $\angle \mathrm{BOD}$ :
$\angle B O Q=\angle Q O D \ldots$(3)
Now,
Sum of the angles around a point is $360^{\circ}$.
$\angle A O C+\angle B O D+\angle A O P+\angle C O P+\angle B O Q+\angle Q O D=360^{\circ}$
$\angle B O Q+\angle Q O D+\angle D O A+\angle A O P+\angle P O C+\angle C O B=360^{\circ}$
$2 \angle \mathrm{QOD}+2 \angle \mathrm{DOA}+2 \angle \mathrm{AOP}=360^{\circ}(\mathrm{Using}(1),(2)$ and $(3))$
$\angle Q O D+\angle D O A+\angle A O P=180^{\circ}$ $\mathrm{POQ}=180^{\circ}$
Which shows that, the bisectors of pair of vertically opposite angles are on the same straight line.
Hence Proved.
Question 6 : If two straight lines intersect each other, prove that the ray opposite to the bisector of one of the angles thus formed bisects the vertically opposite angle.
Solution: Given $\mathrm{AB}$ and $\mathrm{CD}$ are straight lines which intersect at $\mathrm{O}$.
$\mathrm{OP}$ is the bisector of $\angle \mathrm{AOC}$.
To Prove : $\mathrm{OQ}$ is the bisector of $\angle \mathrm{BOD}$
Proof :
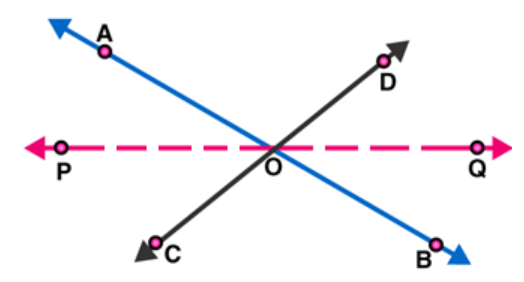
$\mathrm{AB}, \mathrm{CD}$ and $\mathrm{PQ}$ are straight lines which intersect in $\mathrm{O}$.
Vertically opposite angles: $\angle A O P=\angle B O Q$
Vertically opposite angles: $\angle \mathrm{COP}=\angle \mathrm{DOQ}$
OP is the bisector of $\angle A O C: \angle A O P=\angle C O P$
Therefore, $\angle B O Q=\angle D O Q$
Hence, $O Q$ is the bisector of $\angle B O D$.
Exercise $8.4$
Question 1: In figure, $\mathrm{AB}, \mathrm{CD}$ and $\angle 1$ and $\angle 2$ are in the ratio $3: 2$. Determine all angles from 1 to $8 .$
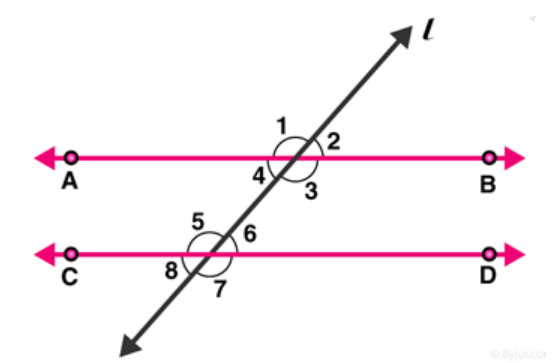
Solution: Let $\angle 1=3 x$ and $\angle 2=2 x$
From figure: $\angle 1$ and $\angle 2$ are linear pair of angles
Therefore, $\angle 1+\angle 2=180$
$3 x+2 x=180$
$5 x=180$
$x=180 / 5$
$=>x=36$
So, $\angle 1=3 x=108^{\circ}$ and $\angle 2=2 x=72^{\circ}$
As we know, vertically opposite angles are equal.
Pairs of vertically opposite angles are:
$(\angle 1=\angle 3) ;(\angle 2=\angle 4) ;(\angle 5, \angle 7)$ and $(\angle 6, \angle 8)$
$\angle 1=\angle 3=108^{\circ}$
$\angle 2=\angle 4=72^{\circ}$
$\angle 5=\angle 7$
$\angle 6=\angle 8$
We also know, if a transversal intersects any parallel lines, then the corresponding angles are equal
$\angle 1=\angle 5=\angle 7=108^{\circ}$
$\angle 2=\angle 6=\angle 8=72^{\circ}$
Answer: $\angle 1=108^{\circ}, \angle 2=72^{\circ}, \angle 3=108^{\circ}, \angle 4$
$108^{\circ}, \angle 4=72^{\circ}, \angle 5$
$\angle 5=108^{\circ}$,
$\angle 6=72^{\circ}, \angle 7$
$=108^{\circ}$ and $\angle 8=72^{\circ}$
Question 2: In figure, I, $m$ and $n$ are parallel lines intersected by transversal $p$ at $X, Y$ and $Z$ respectively. Find $\angle 1, \angle 2$ and $\angle 3$.
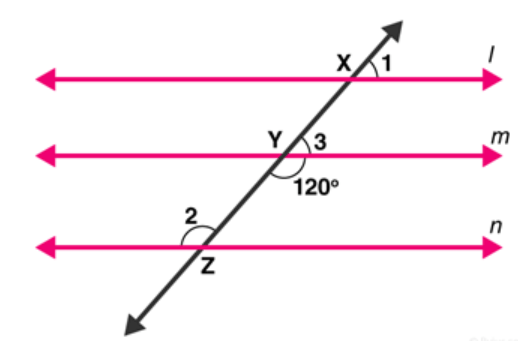
Solution: From figure:
$\angle Y=120^{\circ}[$ Vertical opposite angles $]$
$\angle 3+\angle Y=180^{\circ}$ [Linear pair angles theorem]
$\Rightarrow \angle 3=180-120$
$\Rightarrow \angle 3=60^{\circ}$
Line $I$ is parallel to line $\mathrm{m}$,
$\angle 1=\angle 3$ [ Corresponding angles]
$\angle 1=60^{\circ}$
Also, line $m$ is parallel to line $n$,
$\angle 2=\angle Y$ [Alternate interior angles are equal]
$\angle 2=120^{\circ}$
Answer: $\angle 1=60^{\circ}, \angle 2=120^{\circ}$ and $\angle 3=60^{\circ}$.
Question $3:$ In figure, $A B\|C D\| E F$ and $G H \| K L$. Find $\angle H K L$.
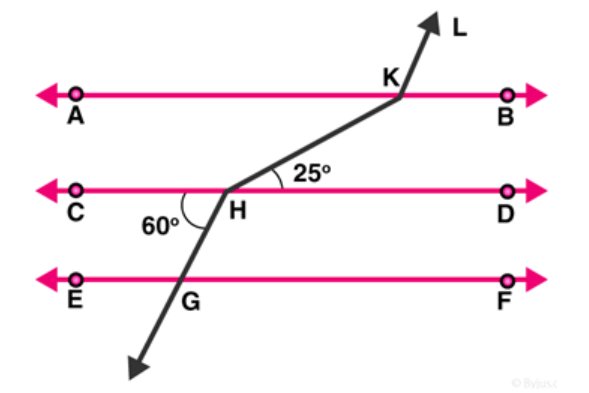
Solution:
Extend LK to meet line GF at point $P$.
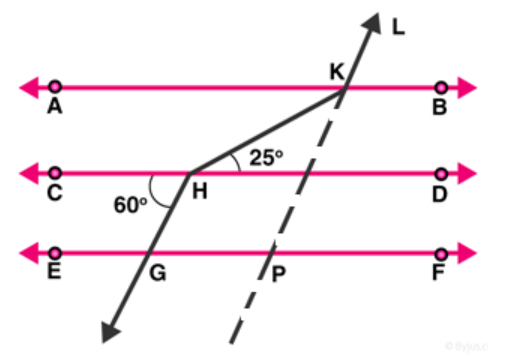
From figure, $\mathrm{CD} \| \mathrm{GF}$, so, alternate angles are equal.
$\angle \mathrm{CHG}=\angle \mathrm{HGP}=60^{\circ}$
$\angle \mathrm{HGP}=\angle \mathrm{KPF}=60^{\circ}$ [Corresponding angles of parallel lines are equal]
Hence, $\angle \mathrm{KPG}=180-60=120^{\circ}$
$\Rightarrow \angle \mathrm{GPK}=\angle \mathrm{AKL}=120^{\circ}$ [Corresponding angles of parallel lines are equal]
$\angle \mathrm{AKH}=\angle \mathrm{KHD}=25^{\circ}$ [alternate angles of parallel lines $]$
Therefore, $\angle \mathrm{HKL}=\angle \mathrm{AKH}+\angle \mathrm{AKL}=25+120=145^{\circ}$
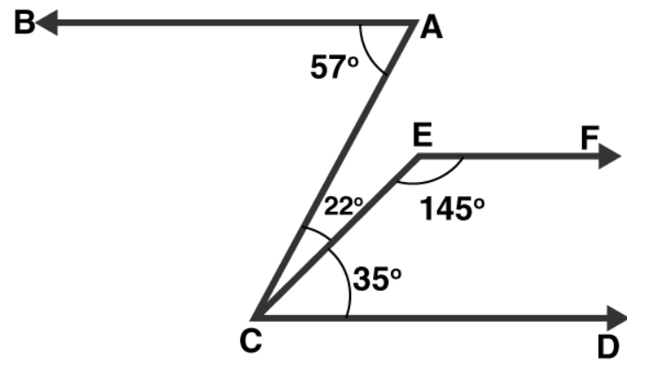
Question 4: In figure, show that AB || EF.
Solution: Produce EF to intersect $\mathrm{AC}$ at point $\mathrm{N}$.
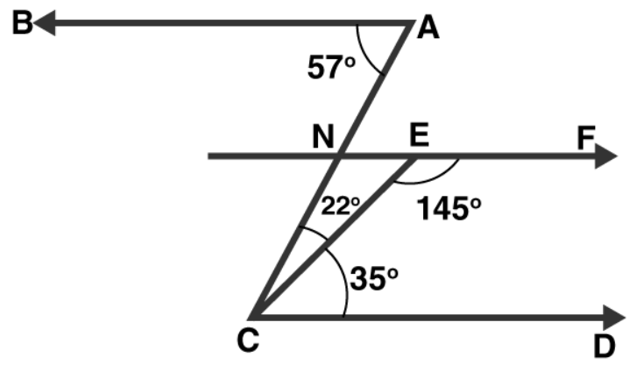
From figure, $\angle B A C=57^{\circ}$ and
$\angle \mathrm{ACD}=22^{\circ}+35^{\circ}=57^{\circ}$
Alternative angles of parallel lines are equal
$\Rightarrow \mathrm{BA} \| \mathrm{EF} \ldots$(1)
Sum of Co-interior angles of parallel lines is $180^{\circ}$
$\mathrm{EF} \| \mathrm{CD}$
$\angle \mathrm{DCE}+\angle \mathrm{CEF}=35+145=180^{\circ}$\ldots(2)$
$\mathrm{AB} \| \mathrm{EF}$
[Since, Lines parallel to the same line are parallel to each other] Hence Proved.
Question 5 : In figure, if $A B$ || $C D$ and CD || EF, find $\angle A C E$.
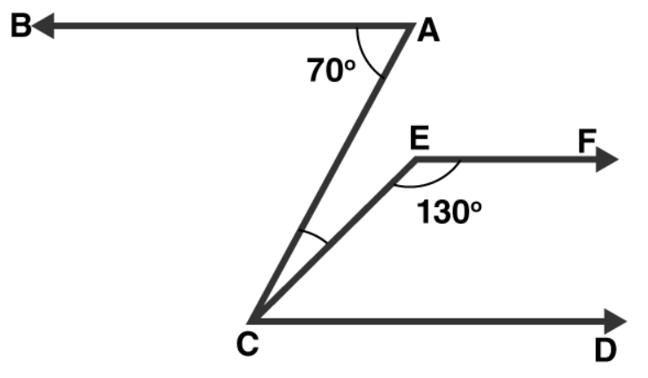
Solution: Given: CD || EF
$\angle \mathrm{FEC}+\angle \mathrm{ECD}=180^{\circ}$
[Sum of co-interior angles is supplementary to each other]
$\Rightarrow \angle \mathrm{ECD}=180^{\circ}-130^{\circ}=50^{\circ}$
Also, BA $\| C D$
$\Rightarrow \angle B A C=\angle A C D=70^{\circ}$
[Alternative angles of parallel lines are equal]
But, $\angle A C E+\angle E C D=70^{\circ}$
$\Rightarrow \angle A C E=70^{\circ}-50^{\circ}=20^{\circ}$
Question 6: In figure, $\mathrm{PQ} \| \mathrm{AB}$ and $\mathrm{PR} \| \mathrm{BC}$. If $\angle \mathrm{QPR}=102^{\circ}$, determine $\angle \mathrm{ABC}$. Give reasons.
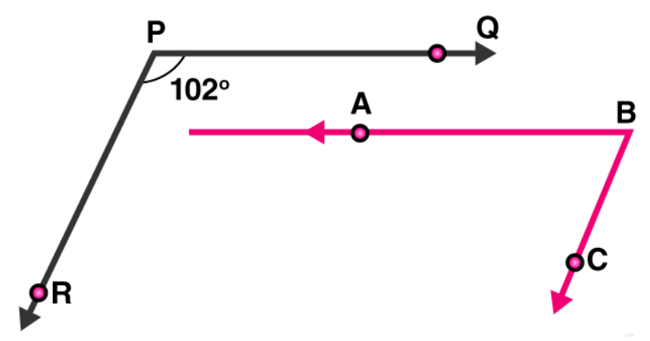
Solution: Extend line $\mathrm{AB}$ to meet line $\mathrm{PR}$ at point $\mathrm{G}$.
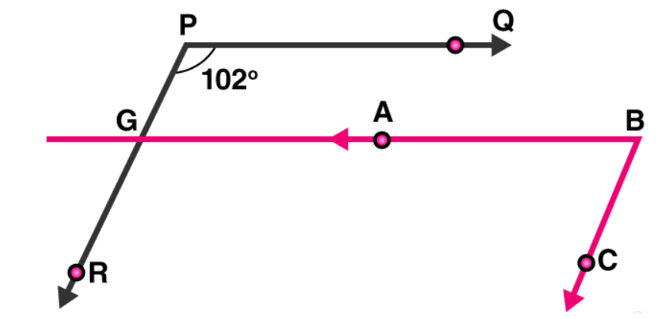
Given: $P Q$ || AB,
$\angle Q P R=\angle B G R=102^{\circ}$
[Corresponding angles of parallel lines are equal]
And PR $\|$ BC,
$\angle R G B+\angle C B G=180^{\circ}$
[Corresponding angles are supplementary]
$\angle \mathrm{CBG}=180^{\circ}-102^{\circ}=78^{\circ}$
Since, $\angle C B G=\angle A B C$
$\Rightarrow \angle A B C=78^{\circ}$
Question 7: In figure, state which lines are parallel and why?
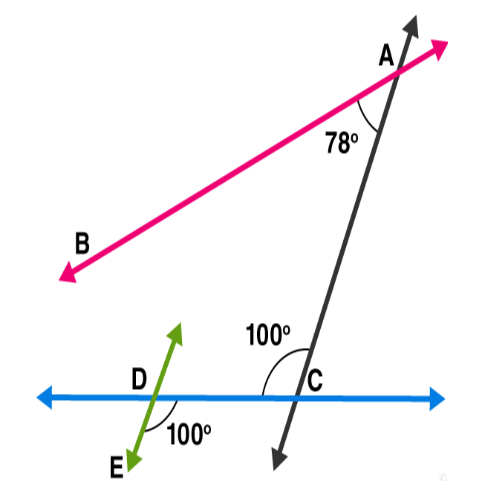
Solution: We know, If a transversal intersects two lines such that a pair of alternate interior angles are equal, then the two lines are parallel
From figure:
$\Rightarrow \angle \mathrm{EDC}=\angle \mathrm{DCA}=100^{\circ}$
Lines DE and AC are intersected by a transversal DC such that the pair of alternate angles are equal.
So, DE $\| A C$
Question 8: In figure, if 1||$m, n \| p$ and $\angle 1=85^{\circ}$, find $\angle 2$.
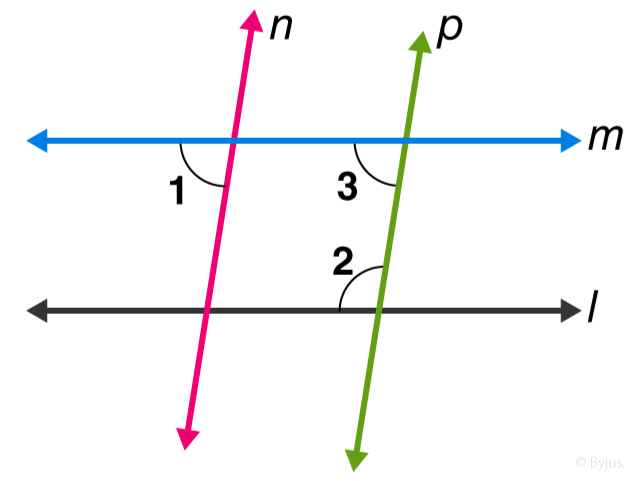
Solution: Given: $\angle 1=85^{\circ}$
As we know, when a line cuts the parallel lines, the pair of alternate interior angles are equal.
$\Rightarrow \angle 1=\angle 3=85^{\circ}$
Again, co-interior angles are supplementary, so
$\angle 2+\angle 3=180^{\circ}$
$\angle 2+55^{\circ}=180^{\circ}$
$\angle 2=180^{\circ}-85^{\circ}$
$\angle 2=95^{\circ}$
Question 9 : If two straight lines are perpendicular to the same line, prove that they are parallel to each other.
Solution: Let lines $\mid$ and $m$ are perpendicular to $n$, then
$\angle 1=\angle 2=90^{\circ}$
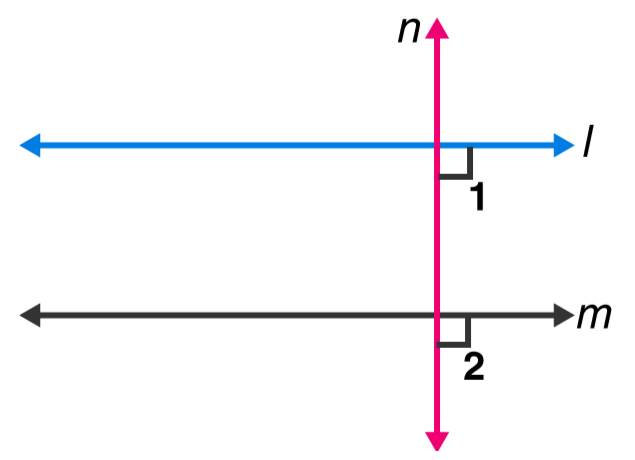
Since, lines $\mid$ and $\mathrm{m}$ cut by a transversal line $\mathrm{n}$ and the corresponding angles are equal, which shows that, line $\mathrm{l}$ is parallel to line $\mathrm{m}$.
Question 10: Prove that if the two arms of an angle are perpendicular to the two arms of another angle, then the angles are either equal or supplementary.
Solution: Let the angles be $\angle A C B$ and $\angle A B D$
Let AC perpendicular to $\mathrm{AB}$, and $\mathrm{CD}$ is perpendicular to $\mathrm{BD}$.
To Prove : $\angle A C D=\angle A B D O R \angle A C D+\angle A B D=180^{\circ}$
Proof :
In a quadrilateral,
$\angle A+\angle C+\angle D+\angle B=360^{\circ}$
[ Sum of angles of quadrilateral is $360^{\circ}$ ]
$\Rightarrow 180^{\circ}+\angle \mathrm{C}+\angle \mathrm{B}=360^{\circ}$
$\Rightarrow \angle \mathrm{C}+\angle \mathrm{B}=360^{\circ}-180^{\circ}$
Therefore, $\angle A C D+\angle A B D=180^{\circ}$
And $\angle A B D=\angle A C D=90^{\circ}$
Hence, angles are equal as well as supplementary.
Exercise VSAQs
Question 1: Define complementary angles.
Solution: When the sum of two angles is 90 degrees, then the angles are known as complementary angles.
Question 2: Define supplementary angles.
Solution: When the sum of two angles is $180^{\circ}$, then the angles are known as supplementary angles.
Question 3: Define adjacent angles.
Solution: Two angles are Adjacent when they have a common side and a common vertex.
Question 4: The complement of an acute angle is_________.
Solution: An acute angle
Question 5: The supplement of an acute angle is___________.
Solution: An obtuse angle
Question 6: The supplement of a right angle is_________.
Solution: A right angle
Also Read,
Download NCERT Class 9 Maths Chapterwise Book Free
Download NCERT Class 10 Maths Chapterwise Book Free
Download NCERT Class 9 Maths Chapterwise Exemplar Free
Download NCERT Class 10 Maths Chapterwise Exemplar Free
If you have any Confusion related to RD Sharma Solutions for Class 9 Maths Chapter 8 Lines and Angles, then feel free to ask in the comments section down below.
To watch Free Learning Videos on Class 9 by Kota’s top Faculties Install the eSaral App
