RD Sharma Solutions for Class 9 Maths Chapter 9 Triangle and its Angles

Hey, are you a class 9 student and looking for ways to download RD Sharma Solutions for Class 9 Maths Chapter 9 "Triangle and its Angles"? If yes. Then read this post till the end.

In this article, we have listed RD Sharma Solutions for Class 9 Maths Chapter 9 in PDF that is prepared by Kota’s top IITian’s Faculties by keeping Simplicity in mind.

If you want to learn and understand class 9 Maths Chapter 9 "Triangle and its Angles" in an easy way then you can use these solutions PDF.

Chapter 9 of RD Sharma Class 9 deals with Triangle and its Angles, their different types and formulas. If you want to improve your basic in Triangle and its Angles, then you can use this.

RD Sharma Solutions helps students to Practice important concepts of subjects easily. RD Sharma class 9 solutions provide detailed explanations of all the  exercise questions that students can use to clear their doubts instantly.

If you want to become good at Math then it is very important for you to have a good knowledge of all the important topics of class 9 math, so to learn and practice those topics you can use eSaral RD Sharma Solutions.

In this article, we have listed RD Sharma Solutions for Class 9 Maths Chapter 9 that you can download to start your preparations anytime.

So, without wasting more time Let’s start.

RD Sharma Solutions for Class 9 Maths Chapter 9 Triangle and its Angles - Free PDF Download

Question 1: In a $\Delta \mathrm{ABC}$, if $\angle A=55^{\circ}, \angle B=40^{\circ}$, find $\angle C$.

Solution: Given: $\angle A=55^{\circ}, \angle B=40^{\circ}$

We know, sum of all angles of a triangle is $180^{\circ}$

$\angle A+\angle B+\angle C=180^{\circ}$

$55^{\circ}+40^{\circ}+\angle C=180^{\circ}$

$95^{\circ}+\angle \mathrm{C}=180^{\circ}$

$\angle C=180^{\circ}-95^{\circ}$

$\angle C=85^{\circ}$

Question 2: If the angles of a triangle are in the ratio $1: 2: 3$, determine three angles.

Solution: Angles of a triangle are in the ratio 1:2:3 (Given)

Let the angles be $x, 2 x, 3 x$

Sum of all angles of triangles $=180^{\circ}$

$x+2 x+3 x=180^{\circ}$

$6 x=180^{\circ}$

$x=180^{\circ} / 6$

$x=30^{\circ}$

Answer:

$\mathrm{x}=30^{\circ}$

$2 x=2(30)^{\circ}=60^{\circ}$

$3 x=3(30)^{\circ}=90^{\circ}$

Question 3: The angles of a triangle are $(x-40)^{\circ},(x-20)^{\circ}$ and $(1 / 2 x-10)^{\circ}$. Find the value of $x$.

Solution: The angles of a triangle are $(x-40)^{\circ},(x-20)^{\circ}$ and $(1 / 2 x-10)^{\circ}$

Sum of all angles of triangle $=180^{\circ}$

$(x-40)^{\circ}+(x-20)^{\circ}+(1 / 2 x-10)^{\circ}=180^{\circ}$

$5 / 2 x-70^{\circ}=1800$

$5 / 2 x=180^{\circ}+70^{\circ}$

$5 x=2(250)^{\circ}$

$\mathrm{x}=500^{\circ} / 5$

$x=100^{\circ}$

Question 4: The angles of a triangle are arranged in ascending order of magnitude. If the difference between two consecutive angles is $10^{\circ}$, find the three angles.

Solution: The difference between two consecutive angles is $10^{\circ}$ (given)

Let $x, x+10^{\circ}, x+20^{\circ}$ be the consecutive angles

$x+x+10^{\circ}+x+20^{\circ}=180^{\circ}$

$3 x=180^{\circ}-30^{\circ}$

$3 x=180^{\circ}-30^{\circ}$

$3 x=150^{\circ}$

or $x=50^{\circ}$

Again,

$x+10^{\circ}=50^{\circ}+10^{\circ}=60^{\circ}$

$x+20^{\circ}=50^{\circ}+20^{\circ}=70$

Question 5: Two angles of a triangle are equal and the third angle is greater than each of those angles by $30^{\circ}$. Determine all the angles of the triangle.

Solution: Two angles of a triangle are equal and the third angle is greater than each of those angles by $30^{\circ}$.

(Given)

Let $x, x, x+30^{\circ}$ be the angles of a triangle.

Sum of all angles in a triangle $=180^{\circ}$

$x+x+x+30^{\circ}=180^{\circ}$

$3 x+30^{\circ}=180^{\circ}$

$3 x=150^{\circ}$

or $x=50^{\circ}$

And $x+30^{\circ}=50^{\circ}+30^{\circ}=80^{\circ}$

Answer: Three angles are $50^{\circ}, 50^{\circ}$ and $80^{\circ}$.

Question $6:$ If one angle of a triangle is equal to the sum of the other two, show that the triangle is a right angle triangle.

Solution: One angle of a triangle is equal to the sum of the other two angles (given)

To Prove: One of the angles is $90^{\circ}$

Let $x, y$ and $z$ are three angles of a triangle, where

$z=x+y \ldots$(1)

Sum of all angles of a triangle $=180^{\circ}$

$x+y+z=180^{\circ}$

$\mathrm{z}+\mathrm{z}=180^{\circ}$ (Using equation (1))

$2 z=180^{\circ}$

$z=90^{\circ}$ (Proved)

Therefore, triangle is a right angled triangle.

Exercise $9.2$ Page No: $9.18$

Question 1: The exterior angles, obtained on producing the base of a triangle both ways are $104^{\circ}$ and $136^{\circ}$. Find all the angles of the triangle.

Solution:



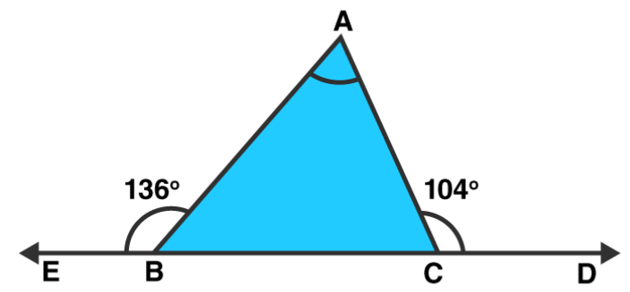
$\angle \mathrm{ACD}=\angle \mathrm{ABC}+\angle \mathrm{BAC}$ [Exterior angle property]

Find $\angle A B C$ :

$\angle \mathrm{ABC}+\angle \mathrm{ABE}=180^{\circ}[\mathrm{Linear}$ pair $]$

$\angle A B C+136^{\circ}=180^{\circ}$

\angle \mathrm{ABC}=44^{\circ}

Find $\angle A C B$ :

$\angle \mathrm{ACB}+\angle \mathrm{ACD}=180^{\circ}$ [Linear pair]

$\angle A C B+104^{\circ}=180^{\circ}$

$\angle A C B=76^{\circ}$

Now,

Sum of all angles of a triangle $=180^{\circ}$

$\angle A+44^{\circ}+76^{\circ}=180^{\circ}$

$\angle A=180^{\circ}-44^{\circ}-76^{\circ}$

$\angle A=60^{\circ}$

Answer: Angles of a triangle are $\angle \mathrm{A}=60^{\circ}, \angle \mathrm{B}=44^{\circ}$ and $\angle \mathrm{C}=76^{\circ}$

Question 2: In a $\triangle A B C$, the internal bisectors of $\angle B$ and $\angle C$ meet at $P$ and the external bisectors of $\angle \mathrm{B}$ and $\angle \mathrm{C}$ meet at $\mathrm{Q}$. Prove that $\angle \mathrm{BPC}+\angle \mathrm{BQC}=180^{\circ}$

Solution: In triangle $A B C$,

$\mathrm{BP}$ and $\mathrm{CP}$ are internal bisector of $\angle \mathrm{B}$ and $\angle \mathrm{C}$ respectively

$\Rightarrow$ External $\angle B=180^{\circ}-\angle B$

$\mathrm{BQ}$ and $\mathrm{CQ}$ are external bisector of $\angle \mathrm{B}$ and $\angle \mathrm{C}$ respectively.

$\Rightarrow$ External $\angle C=180^{\circ}-\angle C$

In triangle BPC,

$\angle \mathrm{BPC}+1 / 2 \angle \mathrm{B}+1 / 2 \angle \mathrm{C}=180^{\circ}$

$\angle B P C=180^{\circ}-1 / 2(\angle B+\angle C) \ldots$(1)

In triangle BQC,

$\angle B Q C+1 / 2\left(180^{\circ}-\angle B\right)+1 / 2\left(180^{\circ}-\angle C\right)=180$

$\angle B Q C+180^{\circ}-1 / 2(\angle B+\angle C)=180$

$\angle \mathrm{BPC}+\angle \mathrm{BQC}=180^{\circ}[\mathrm{Using}(1)]$

Hence Proved.

Question 3: In figure, the sides $\mathrm{BC}, \mathrm{CA}$ and $\mathrm{AB}$ of a $\triangle \mathrm{ABC}$ have been produced to $\mathrm{D}, \mathrm{E}$ and $\mathrm{F}$ respectively. If $\angle A C D=105^{\circ}$ and $\angle E A F=45^{\circ}$, find all the angles of the $\triangle A B C$.



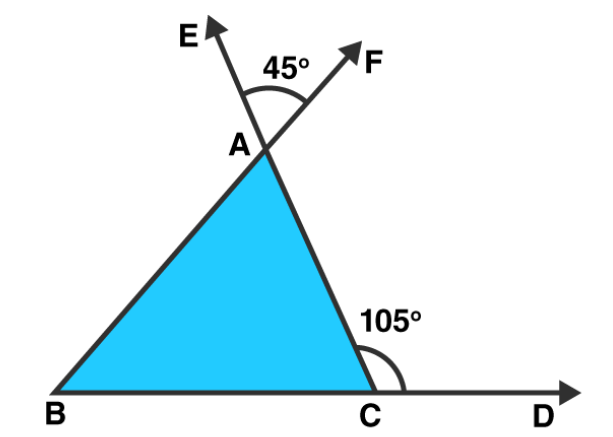
Solution: $\angle B A C=\angle E A F=45^{\circ}[$ Vertically opposite angles $]$

$\angle \mathrm{ACD}=180^{\circ}-105^{\circ}=75^{\circ}$ [Linear pair]

$\angle A B C=105^{\circ}-45^{\circ}=60^{\circ}$ [Exterior angle property]

Question 4: Compute the value of $x$ in each of the following figures:

(i)



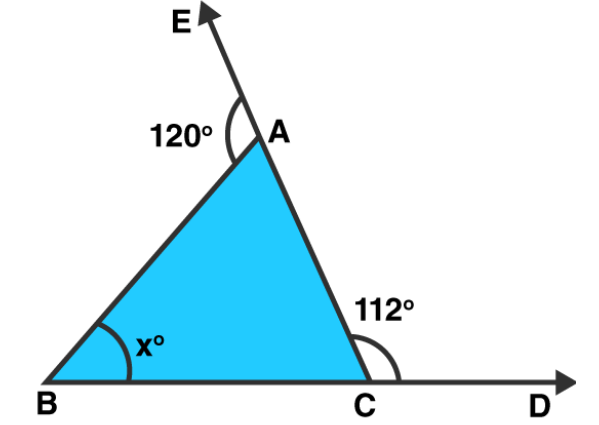
Solution: $\angle B A C=180^{\circ}-120^{\circ}=60^{\circ}$ [Linear pair]

$\angle \mathrm{ACB}=180^{\circ}-112^{\circ}=68^{\circ}$ [Linear pair]

Sum of all angles of a triangle $=180^{\circ}$

$x=180^{\circ}-\angle B A C-\angle A C B$

$=180^{\circ}-60^{\circ}-68^{\circ}=52^{\circ}$

Answer: $x=52^{\circ}$

(ii)



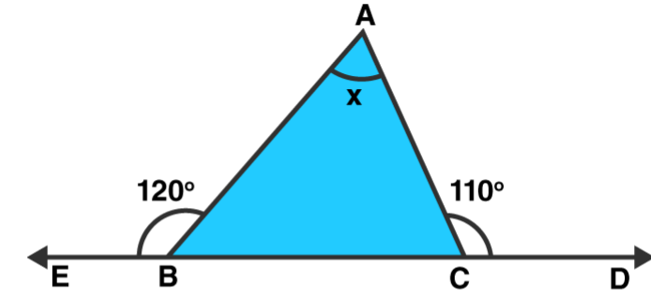
Solution: $\angle \mathrm{ABC}=180^{\circ}-120^{\circ}=60^{\circ}$ [Linear pair]

$\angle \mathrm{ACB}=180^{\circ}-110^{\circ}=70^{\circ}$ [Linear pair]

Sum of all angles of a triangle $=180^{\circ}$

$\mathrm{x}=\angle \mathrm{BAC}=180^{\circ}-\angle \mathrm{ABC}-\angle \mathrm{ACB}$

$=180^{\circ}-60^{\circ}-70^{\circ}=50^{\circ}$

Answer: $x=50^{\circ}$

(iii)



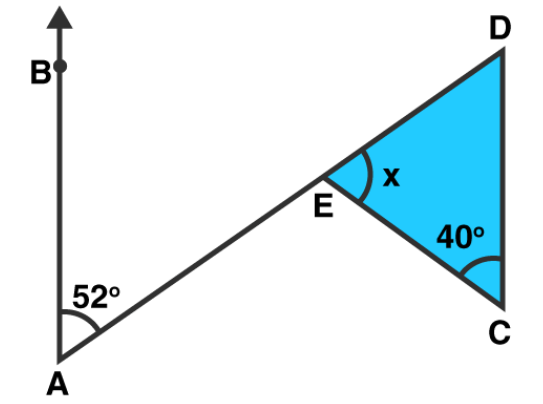
Solution: $\angle \mathrm{BAE}=\angle \mathrm{EDC}=52^{\circ} \text { [Alternate angles] }$

Sum of all angles of a triangle $=180^{\circ}$

$x=180^{\circ}-40^{\circ}-52^{\circ}=180^{\circ}-92^{\circ}=88^{\circ}$

Answer: $x=88^{\circ}$

(iv)



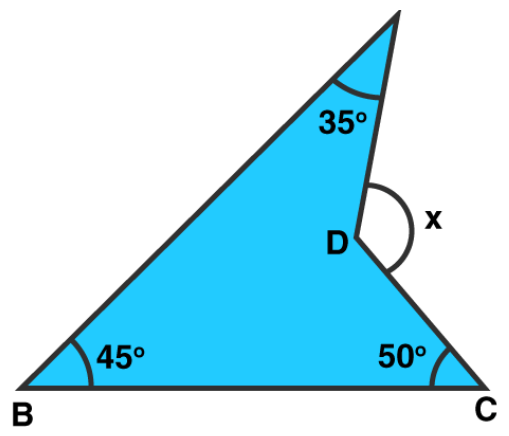
Solution:

$\mathrm{CD}$ is produced to meet $\mathrm{AB}$ at $\mathrm{E}$.



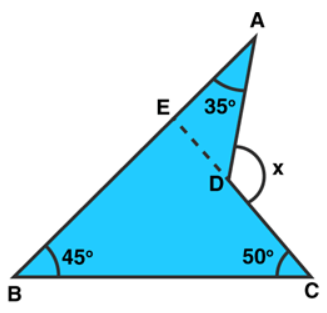
$\angle \mathrm{BEC}=180^{\circ}-45^{\circ}-50^{\circ}=85^{\circ}\left[\right.$ Sum of all angles of a triangle $\left.=180^{\circ}\right]$

$\angle \mathrm{AEC}=180^{\circ}-85^{\circ}=95^{\circ}$ [Linear Pair]

Now, $x=95^{\circ}+35^{\circ}=130^{\circ}$ [Exterior angle Property]

Answer: $x=130^{\circ}$

Question 5: In figure, AB divides $\angle D A C$ in the ratio $1: 3$ and $A B=D B$. Determine the value of $\mathbf{x}$



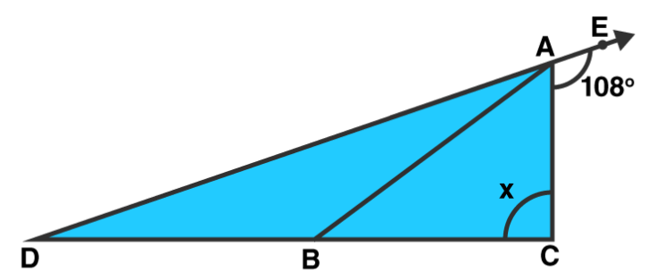
Solution: $\angle \mathrm{DAC}=180^{\circ}-108^{\circ}=72^{\circ}$

$\angle B A C / \angle D A B=1 / 3$

$\angle \mathrm{DAB}=3 \angle \mathrm{BAC}$

$\angle B A C+\angle D A B=\angle D A C=72^{\circ}$

We can write it as

$\angle B A C+3 \angle B A C=72^{\circ}$

$4 \angle \mathrm{BAC}=72^{\circ}$

$\angle B A C=72 / 4=18^{\circ}$

So we get

$\angle \mathrm{DAB}=3 \times 18^{\circ}=54^{\circ}$

$\angle D A B=\angle B D A=54^{\circ}(A B=D B)$

$\angle \mathrm{ABD}=180^{\circ}-\left(54^{\circ}+54^{\circ}\right)$

$=180-108^{\circ}$

$=72^{\circ}$

Now,

$\angle \mathrm{DBA}=72^{\circ}=\angle \mathrm{BAC}+\mathrm{x} \text { (Exterior angle) }$

So we get

$\mathrm{x}=72^{\circ}-18^{\circ}=54^{\circ}$

Exercise VSAQs Page No: $9.21$

Question 1: Define a triangle.

Solution: Triangle is a three-sided polygon that consists of three edges and three vertices. The most important property of a triangle is that the sum of the internal angles of a triangle is equal to 180 degrees.

Question 2: Write the sum of the angles of an obtuse triangle.

Solution: The sum of angles of obtuse triangle $=180^{\circ}$.

Question 3: In $\triangle A B C$, if $\angle B=60^{\circ}, \angle C=80^{\circ}$ and the bisectors of angles $\angle A B C$ and $\angle A C B$ meet at point $O$, then find the measure of $\angle B O C$.

Solution: $\angle B=60^{\circ}, \angle C=80^{\circ} \text { (given) }$

As per question:

$\angle \mathrm{OBC}=60^{\circ} / 2=30^{\circ}$ and

$\angle \mathrm{OCB}=80^{\circ} / 2=40^{\circ}$

In triangle BOC,

$\angle \mathrm{OBC}+\angle \mathrm{OCB}+\angle \mathrm{BOC}=180^{\circ}$

[Sum of angles of a triangle $\left.=180^{\circ}\right]$

$30^{\circ}+40^{\circ}+\angle B O C=180^{\circ}$

$\angle B O C=110^{\circ}$

Question 4: If the angles of a triangle are in the ratio $2: 1: 3$, then find the measure of smallest angle.

Solution: Let angles of a triangles are $2 x, x$ and $3 x$, where $x$ is the smallest angle.

To find: measure of $x$.

As, Sum of angles of a triangle $=180^{\circ}$

$2 x+x+3 x=180^{\circ}$

$6 x=180^{\circ}$

$\mathrm{x}=30^{\circ}$. Answer

Question 5 : If the angles $A, B$ and $C$ of $\triangle A B C$ satisfy the relation $B-A=C-B$, then find the measure of $\angle B$.

Solution: Sum of angles of a triangle $=180^{\circ}$

$A+B+C=180^{\circ} \ldots(1)$

$\mathrm{B}-\mathrm{A}=\mathrm{C}-\mathrm{B} \ldots($ Given $)$

$2 B=C+A \ldots(2)$

$(1)=>2 B+B=180^{\circ}$

$3 B=180^{\circ}$

Or $B=60^{\circ}$

Also Read,

Download NCERT Class 9 Maths Chapterwise Book Free PDF

Download NCERT Class 10 Maths Chapterwise Book Free PDF

Download NCERT Class 9 Maths Chapterwise Exemplar Free PDF

Download NCERT Class 10 Maths Chapterwise Exemplar Free PDF

If you have any Confusion related to RD Sharma Solutions for Class 9 Maths Chapter 9 Triangle and its Angles, then feel free to ask in the comments section down below.

To watch Free Learning Videos on Class 9 by Kota’s top Faculties Install the eSaral App