Q. A thin uniform rod of length l and mass m is swinging freely about a horizontal axis passing through its end. Its maximum angular speed is $\omega$. Its centre of mass rises to a maximum height of:
(1) $\frac{1}{2} \frac{l^{2} \omega^{2}}{g}$
(2) $\frac{1}{6} \frac{l^{2} \omega^{2}}{9}$
(3) $\frac{1}{3} \frac{l^{2} \omega^{2}}{9}$
( 4)$\frac{1}{6} \frac{l \omega}{g}$
[AIEEE – 2009]
Q. A small particle of mass $\mathrm{m}$ is projected at an angle $\theta$ with the $\mathrm{x}$ -axis with an initial velocity $\mathrm{v}_{0}$
in the $\mathrm{x}$ -y plane as shown in the figure. At a time $\mathrm{t}<\frac{\mathrm{v}_{0} \sin \theta}{\mathrm{g}},$ the angular momentum of the
particle is: Where $\hat{\mathrm{i}}, \hat{\mathrm{j}}$ and $\hat{\mathrm{k}}$ are unit vectors along $\mathrm{x}$, y and $\mathrm{z}$ -axis respectively.
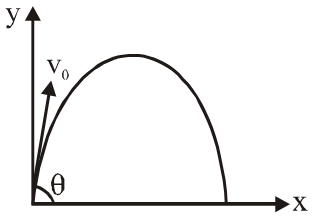(1) $\frac{1}{2} \mathrm{mg} \mathrm{v}_{0} \mathrm{t}^{2} \cos \theta \hat{\mathrm{i}}$
(2) $-\mathrm{mg} \mathrm{v}_{0} \mathrm{t}^{2} \cos \theta \hat{\mathrm{j}}$
(3) $\operatorname{mg} \mathrm{v}_{0}$ t $\cos \theta \hat{\mathrm{k}}$
(4)-\frac{1}{2} \operatorname{mg} v_{0} t^{2} \cos \theta \hat{k}
[AIEEE-2010]
(1) $\frac{1}{2} \mathrm{mg} \mathrm{v}_{0} \mathrm{t}^{2} \cos \theta \hat{\mathrm{i}}$
(2) $-\mathrm{mg} \mathrm{v}_{0} \mathrm{t}^{2} \cos \theta \hat{\mathrm{j}}$
(3) $\operatorname{mg} \mathrm{v}_{0}$ t $\cos \theta \hat{\mathrm{k}}$
(4)-\frac{1}{2} \operatorname{mg} v_{0} t^{2} \cos \theta \hat{k}
[AIEEE-2010]
Q. A pulley of radius 2 m is rotated about its axis by a force \mathrm{F}=\left(20 \mathrm{t}-5 \mathrm{t}^{2}\right) newton (where t is measured in seconds) applied tangentially. If the moment of inertia of the pulley about its axis of rotationis 10 kg \mathrm{m}^{2}, the number of rotations made by the pulley before its direction of motion it reversed, is :-
(1) more than 6 but less than 9
(2) more than 9
(3) less than 3
(4) more than 3 but less than 6
[AIEEE-2011]
Q. A thin horizontal circular disc is rotating about a vertical axis passing through its centre. An insect is at rest at a point near the rim of the disc. The insect now moves along a diameter of the disc to reach its other end. Euring the fjourney of the insect, then angular speed of the disc :-
[AIEEE-2011]
Q. A particle of mass ‘m’ is projected with a velocity v making an angle of 30^{\circ} with the horizontal. The magnitude of angular momentum of the projectile about the point of projection when the particle is at its maximum height ‘h’ is :-
(1) $\frac{\sqrt{3}}{2} \frac{\mathrm{mv}^{2}}{9}$
(2) zero
(3) $\frac{\mathrm{mv}^{3}}{\sqrt{2} \mathrm{g}}$
(4) $\frac{\sqrt{3}}{16} \frac{\mathrm{mv}^{3}}{\mathrm{g}}$
[AIEEE-2011]
Q. A hoop of radius r and mass m rotating with an angular velocity $\omega_{0}$ is placed on a rough horizontal surface. The initial velocity of the centre of the hoop is zero. What will be the velocity of the centre of the hoop when it ceases to slip?
(1) $\frac{\mathrm{r\omega}_{0}}{4}$
( 2)$\frac{\mathrm{r} \omega_{0}}{3}$
(3) $\frac{\mathrm{r} \omega_{0}}{2}$
(4) $\mathrm{r\omega}_{0}$
[JEE Mains-2013]
Q. A bob of mass m attached to an inextensible string of length is suspended from a vertical support. The bob rotates in a horizontal circle with an angular speed rad/s about the vertical. About the point of suspension :
(1) Angular momentum changes in direction but not in magnitude
(2) Angular momentum changes both in direction and magnitude
(3) Angular momentum is conserved
(4) Angular momentum changes in magnitude but not in direction.
[JEE Mains-2014]
Q. A mass ‘m’ is supported by a massless string wound around a uniform hollow cylinder of mass m and radius R. If the string does not slip on the cylinder, with what acceleration will the mass fall on release?
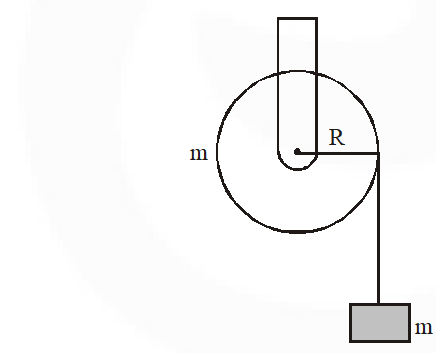(1) $\frac{5 \mathrm{g}}{6}$ (2) g (3) $\frac{2 \mathrm{g}}{3}$ (4) $\frac{\mathrm{g}}{2}$
[JEE Mains-2014]
(1) $\frac{5 \mathrm{g}}{6}$ (2) g (3) $\frac{2 \mathrm{g}}{3}$ (4) $\frac{\mathrm{g}}{2}$
[JEE Mains-2014]
Q. From a solid sphere of mass M and radius R a cube of maximum possible volume is cut. Moment of inertia of cube about an axis passing through its centre and perpendicular to one of its faces is:-
(1) $\frac{4 \mathrm{MR}^{2}}{9 \sqrt{3} \pi}$
(2) $\frac{4 \mathrm{MR}^{2}}{3 \sqrt{3 \pi}}$
(3) $\frac{\mathrm{MR}^{2}}{32 \sqrt{2} \pi}$
(4) $\frac{\mathrm{MR}^{2}}{16 \sqrt{2} \pi}$
[JEE Mains-2015]
Q. A particle of mass m is moving along the side of a square of side ‘a’, with a uniform speed in the x-y plane as shown in the figure :
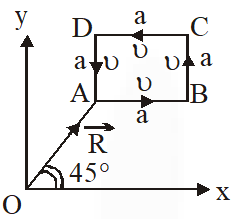Which of the following statement is false for the angular momentum $\overrightarrow{\mathrm{L}}$ about the origin ?
(1) $\overrightarrow{\mathrm{L}}=\frac{\mathrm{mv}}{\sqrt{2}} \mathrm{R} \hat{\mathrm{k}}$ when the particle is moving from $\mathrm{D}$ to $\mathrm{A}$
(2) $\overrightarrow{\mathrm{L}}=-\frac{\mathrm{mv}}{\sqrt{2}} \mathrm{R} \hat{\mathrm{k}}$ when the particle is moving from $\mathrm{A}$ to $\mathrm{B}$
(3) $\overrightarrow{\mathrm{L}}=\mathrm{mu}\left[\frac{\mathrm{R}}{\sqrt{2}}-\mathrm{a}\right] \hat{\mathrm{k}}$ when the particle is moving from $\mathrm{C}$ to $\mathrm{D}$
(4) $\overrightarrow{\mathrm{L}}=\mathrm{mv}\left[\frac{\mathrm{R}}{\sqrt{2}}+\mathrm{a}\right] \hat{\mathrm{k}}$ when the particle is moving from $\mathrm{B}$ to $\mathrm{C}$
[JEE Mains-2016]
Which of the following statement is false for the angular momentum $\overrightarrow{\mathrm{L}}$ about the origin ?
(1) $\overrightarrow{\mathrm{L}}=\frac{\mathrm{mv}}{\sqrt{2}} \mathrm{R} \hat{\mathrm{k}}$ when the particle is moving from $\mathrm{D}$ to $\mathrm{A}$
(2) $\overrightarrow{\mathrm{L}}=-\frac{\mathrm{mv}}{\sqrt{2}} \mathrm{R} \hat{\mathrm{k}}$ when the particle is moving from $\mathrm{A}$ to $\mathrm{B}$
(3) $\overrightarrow{\mathrm{L}}=\mathrm{mu}\left[\frac{\mathrm{R}}{\sqrt{2}}-\mathrm{a}\right] \hat{\mathrm{k}}$ when the particle is moving from $\mathrm{C}$ to $\mathrm{D}$
(4) $\overrightarrow{\mathrm{L}}=\mathrm{mv}\left[\frac{\mathrm{R}}{\sqrt{2}}+\mathrm{a}\right] \hat{\mathrm{k}}$ when the particle is moving from $\mathrm{B}$ to $\mathrm{C}$
[JEE Mains-2016]
Download eSaral App for Video Lectures, Complete Revision, Study Material and much more...
Sol. (1,3)
Q. A roller is made by joining together two cones at their vertices O. It is kept on two rails AB and CD which are placed asymmetrically (see figure), with its axis perpendicular to CD and its centre O at the centre of line joining AB and CD (see figure). It is given a light push so that it starts rolling with its centre O moving parallel to CD in the direction shown. As it moves, the roller will tend to :-
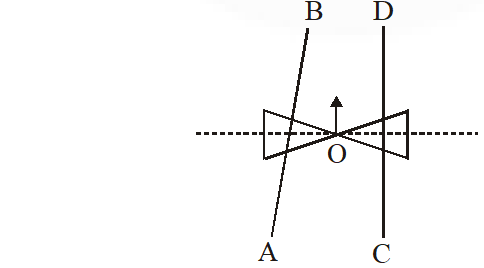(1) turn left and right alternately.
(2) turen left.
(3) turn right.
(4) go straight.
[JEE Mains-2016]
(1) turn left and right alternately.
(2) turen left.
(3) turn right.
(4) go straight.
[JEE Mains-2016]
Q. The moment of inertia of a uniform cylinder of length and radius R about its perpendicular bisector is I. What is the ratio /R such that the moment of inertia is minimum ?
(1) 1
(2) $\frac{3}{\sqrt{2}}$
(3) $\sqrt{\frac{3}{2}}$
(4) $\frac{\sqrt{3}}{2}$
[JEE Mains-2017]
Q. A slender uniform rod of mass M and length is pivoted at one end so that it can rotate in a vertical plane (see figure). There is negligible friction at the pivot. The free end is held vertically above the pivot and then released. The angular acceleration of the rod when it makes an angle $\theta$ with the vertical is :
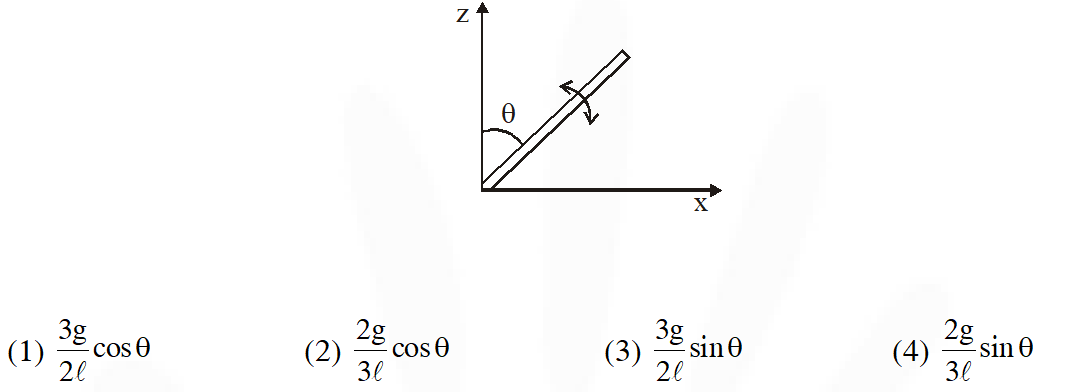[JEE Mains-2017]
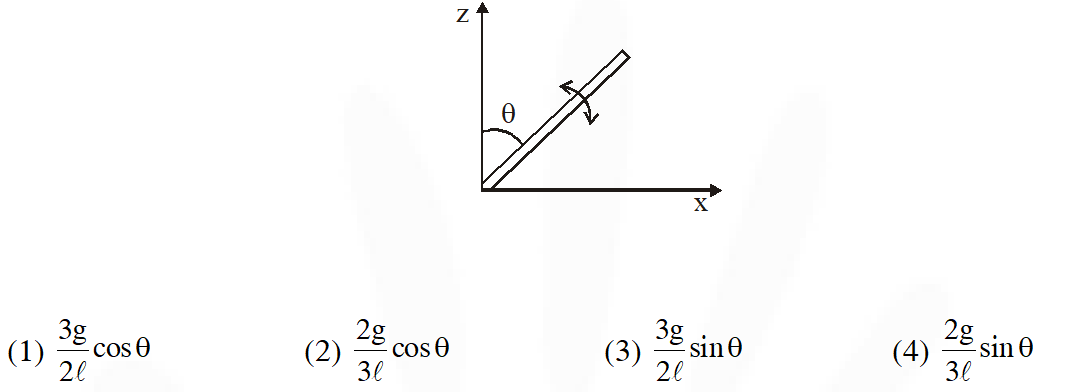[JEE Mains-2017]
Q. From a uniform circular disc of radius R and mass 9M, a small disc of radius $\frac{\mathrm{R}}{3}$ is removed as shown in the figure. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through centre of disc is :
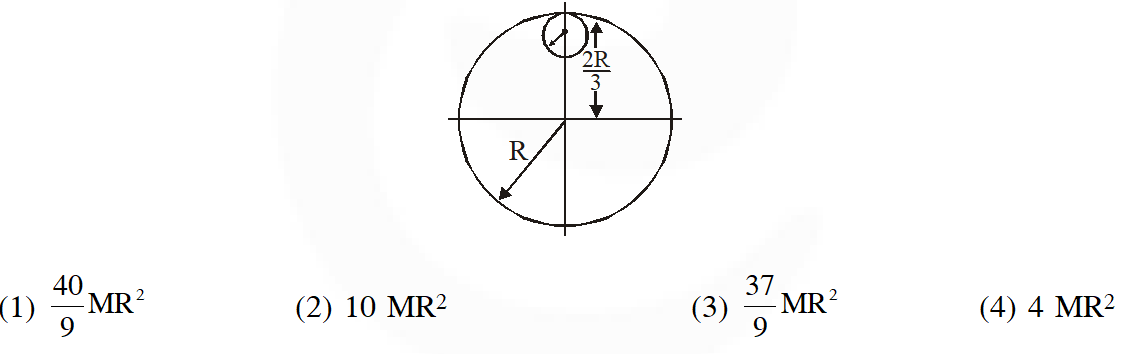[JEE Mains-2018]
[JEE Mains-2018]
Q. Seven identical circular planar disks, each of mass M and radius R are welded symmetrically as shown. The moment of inertia of the arrangement about the axis normal to the plane and passing through the point P is :
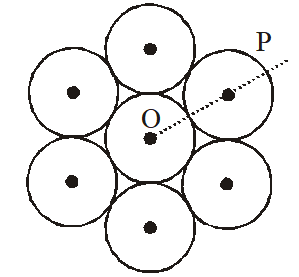(1) $\frac{55}{2} \mathrm{MR}^{2}$
(2) $\frac{73}{2} \mathrm{MR}^{2}$
(3) $\frac{181}{2} \mathrm{MR}^{2}$
(4) $\frac{19}{2} \mathrm{MR}^{2}$
[JEE Mains-2018]
(1) $\frac{55}{2} \mathrm{MR}^{2}$
(2) $\frac{73}{2} \mathrm{MR}^{2}$
(3) $\frac{181}{2} \mathrm{MR}^{2}$
(4) $\frac{19}{2} \mathrm{MR}^{2}$
[JEE Mains-2018]
Please try to give new questions of 2019 and 2020
very easy questions
Good stuffs
aaaaaaaaaaaaaaaaaa
aaaaaaaaaaaaa
LOW STANDARD QUESTIONS
Madarchod sol nahi diya teri bb ko chodu sol dede randve badu land ter
Dude these questions are asked in JEE Main so you can find their solutions anyway easily
bsdk gali kyo de raha h itni
Thank you for your collection of questions but it is somewhat difficult to understand some values given in questions so please improve it
Would be great if questions of higher difficulty are added
Please improve the writting of questions