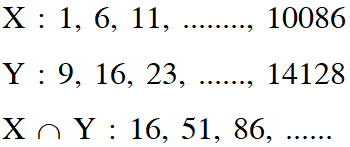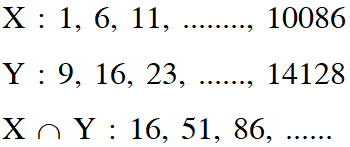JEE Advanced Previous Year Questions of Math with Solutions are available at eSaral. Practicing JEE Advanced Previous Year Papers Questions of mathematics will help the JEE aspirants in realizing the question pattern as well as help in analyzing weak & strong areas.
eSaral helps the students in clearing and understanding each topic in a better way. eSaral also provides complete chapter-wise notes of Class 11th and 12th both for all subjects.
Besides this, eSaral also offers NCERT Solutions, Previous year questions for JEE Main and Advance, Practice questions, Test Series for JEE Main, JEE Advanced and NEET, Important questions of Physics, Chemistry, Math, and Biology and many more.
Download eSaral app for free study material and video tutorials.
Q. If the sum of first $n$ terms of an A.P. is $\mathrm{c} n^{2},$ then the sum of squares of these $n$ terms is
(A) $\frac{\mathrm{n}\left(4 \mathrm{n}^{2}-1\right) \mathrm{c}^{2}}{6}$
(B) $\frac{\mathrm{n}\left(4 \mathrm{n}^{2}+1\right) \mathrm{c}^{2}}{3}$
(C) $\frac{\mathrm{n}\left(4 \mathrm{n}^{2}-1\right) \mathrm{c}^{2}}{3}$
(D) $\frac{n\left(4 n^{2}+1\right) c^{2}}{6}$
[JEE 2009, 3 (–1)]
Ans. (C)
$\mathrm{C}$
$\mathrm{S}_{\mathrm{n}}=\mathrm{cn}^{2}$
$\mathrm{S}_{\mathrm{n}-1}=\mathrm{c}(\mathrm{n}-1)^{2}$
$\mathrm{T}_{\mathrm{n}}=\mathrm{S}_{\mathrm{n}}-\mathrm{S}_{\mathrm{n}-1}=\mathrm{c}(2 \mathrm{n}-1)$
$\mathrm{T}_{\mathrm{n}}^{\prime}=\mathrm{T}_{\mathrm{n}}^{2}=\mathrm{c}^{2}\left(4 \mathrm{n}^{2}-4 \mathrm{n}+1\right)$
$\sum \mathrm{T}_{\mathrm{n}}^{\prime}=\mathrm{nc}^{2}\left(\frac{4 \mathrm{n}^{2}-1}{3}\right)$
Q. Let $a_{1}, a_{2}, a_{3}, \ldots \ldots \ldots a_{11}$ be real numbers satisfying
$\mathrm{a}_{1}=15,27-2 \mathrm{a}_{2}>0$ and $\mathrm{a}_{\mathrm{k}}=2 \mathrm{a}_{\mathrm{k}-1}-\mathrm{a}_{\mathrm{k}-2}$ for $\mathrm{k}=3,4 \ldots \ldots \ldots 11$
If $\frac{a_{1}^{2}+a_{2}^{2}+\ldots \ldots+a_{11}^{2}}{11}=90,$ then the value of $\frac{a_{1}+a_{2}+\ldots \ldots+a_{11}}{11}$ is equal to
[JEE 2010,3+3]
Ans. 0




Q. The minimum value of the sum of real numbers $a^{-5}, a^{-4}, 3 a^{-3}, 1, a^{8}$ and $a^{10}$ with $a>0$ is
[JEE 2011, 4]
Ans. 8
As $a>0$
and all the given terms are positive
hence considering A.M. $\geq$ G.M. for given numbers :
$\frac{\mathrm{a}^{-5}+\mathrm{a}^{-4}+\mathrm{a}^{-3}+\mathrm{a}^{-3}+\mathrm{a}^{-3}+\mathrm{a}^{8}+\mathrm{a}^{10}}{7} \geq\left(\mathrm{a}^{-5} \cdot \mathrm{a}^{-4} \cdot \mathrm{a}^{-3} \cdot \mathrm{a}^{-3} \cdot \mathrm{a}^{-3} \cdot \mathrm{a}^{10}\right)^{\frac{1}{7}}$
$\Rightarrow \frac{\mathrm{a}^{-5}+\mathrm{a}^{-4}+\mathrm{a}^{-3}+\mathrm{a}^{-3}+\mathrm{a}^{-3}+\mathrm{a}^{8}+\mathrm{a}^{10}}{7} \geq 1 \quad \Rightarrow\left(\mathrm{a}^{-5}+\mathrm{a}^{-4}+3 \mathrm{a}^{-3}+\mathrm{a}^{-3}+\mathrm{a}^{10}\right)_{\min }=7$
where $\mathrm{a}^{-5}=\mathrm{a}^{-4}=\mathrm{a}^{-3}=\mathrm{a}^{8}=\mathrm{a}^{10}$ i.e. $\mathrm{a}=1$
$\Rightarrow\left(\mathrm{a}^{-5}+\mathrm{a}^{-4}+3 \mathrm{a}^{-3}+\mathrm{a}^{8}+\mathrm{a}^{10}+1\right)_{\min }=8 \quad$ when $\mathrm{a}=1$
Q. Let $a_{1}, a_{2}, a_{3}, \ldots \ldots \ldots, a_{100}$ be an arithmetic progression with $a_{1}=3$ and $S_{p}=\sum_{i=1}^{p} a_{i}, 1 \leq p \leq 100 .$ For any integer $n$ with $1 \leq n \leq 20,$ let $m=5 n .$ If $\frac{S_{m}}{S_{n}}$ does not depend on n, then $a_{2}$ is
[JEE 2011, 4]
Ans. 9 or 3
9 or 3
(Comment : The information about the common difference i.e. zero or non-zero is not given in the question. Hence there are two possible answers)
Consider $\mathrm{d} \neq 0$ the solution is
$\mathrm{a}_{1}, \mathrm{a}_{2}, \mathrm{a}_{3}, \ldots \ldots \ldots \ldots ., \mathrm{a}_{100} \rightarrow \mathrm{AP}$
$\mathrm{a}_{1}=3 ; \quad \mathrm{S}_{\mathrm{p}}=\sum_{\mathrm{i}=1}^{\mathrm{p}} \mathrm{a}_{\mathrm{i}} \quad 1 \leq \mathrm{n} \leq 20$
$\mathrm{m}=5 \mathrm{n}$
$\frac{\mathrm{S}_{\mathrm{m}}}{\mathrm{S}_{\mathrm{n}}}=\frac{\frac{\mathrm{m}}{2}\left[2 \mathrm{a}_{1}+(\mathrm{m}-1) \mathrm{d}\right]}{\frac{\mathrm{n}}{2}\left[2 \mathrm{a}_{1}+(\mathrm{n}-1) \mathrm{d}\right]}$
$\frac{\mathrm{S}_{\mathrm{m}}}{\mathrm{S}_{\mathrm{n}}}=\frac{5\left[\left(2 \mathrm{a}_{1}-\mathrm{d}\right)+5 \mathrm{nd}\right]}{\left[\left(2 \mathrm{a}_{1}-\mathrm{d}\right)+\mathrm{nd}\right]}$ for $\frac{\mathrm{S}_{\mathrm{m}}}{\mathrm{S}_{\mathrm{n}}}$ to be independent of $\mathrm{n}$
$\begin{array}{ll}{\therefore 2 \mathrm{a}_{1}-\mathrm{d}=0} & {\Rightarrow \mathrm{d}=2 \mathrm{a}_{1} \Rightarrow \mathrm{d}=6 \Rightarrow \mathrm{a}_{2}=9} \\ {\text { If } \mathrm{d}=0 \quad \Rightarrow} & {\mathrm{a}_{2}=\mathrm{a}_{1}=3}\end{array}$
Q. Let $a_{1}, a_{2}, a_{3}, \ldots .$ be in harmonic progression with $a_{1}=5$ and $a_{20}=25 .$ The least positive integer n for which $a_{n}<0$ is
(A) 22 (B) 23 (C) 24 (D) 25
[JEE 2012, 3 (–1)]
Ans. (D)
$a_{1}, a_{2}, a_{3} \dots \ldots . .$ be in $\mathrm{H.P} \Rightarrow \frac{1}{\mathrm{a}_{1}}, \frac{1}{\mathrm{a}_{2}}, \frac{1}{\mathrm{a}_{3}} \ldots$ be in A.P.
in A.P. $\mathrm{T}_{1}=\frac{1}{\mathrm{a}_{1}}=\frac{1}{5}$ and $\mathrm{T}_{20}=\frac{1}{\mathrm{a}_{20}}=\frac{1}{25}$
$\therefore \mathrm{T}_{20}=\mathrm{T}_{1}+19 \mathrm{d}$
$\frac{1}{25}=\frac{1}{5}+19 \mathrm{d} \Rightarrow \mathrm{d}=-\frac{4}{19 \times 25}$
$\mathrm{T}_{\mathrm{n}}=\mathrm{T}_{1}+(\mathrm{n}-1) \mathrm{d}<0 \Rightarrow \frac{1}{5}-\frac{(\mathrm{n}-1) \cdot 4}{19 \times 25}<0 \quad \Rightarrow \frac{1}{5}<\frac{4(\mathrm{n}-1)}{25 \times 19} \Rightarrow \frac{5 \times 19}{4}+1<\mathrm{n} \Rightarrow \frac{99}{4}<\mathrm{n}$
$\Rightarrow$ least positive integer $n$ is 25
Q. Let $\mathrm{S}_{\mathrm{n}}=\sum_{\mathrm{k}=1}^{4 \mathrm{n}}(-1)^{\frac{\mathrm{k}(\mathrm{k}+1)}{2}} \mathrm{k}^{2} .$ Then $\mathrm{S}_{\mathrm{n}}$ can take value(s)
(A) 1056 (B) 1088 (C) 1120 (D) 1332
[JEE-Advanced 2013, 4, (–1)]
Ans. (A,D)
$\mathrm{S}_{\mathrm{n}}=-1^{2}-2^{2}+3^{2}+4^{2}-5^{2}-6^{2}+7^{2}+8^{2} \ldots \ldots \ldots$
$\mathrm{S}_{\mathrm{n}}^{\mathrm{n}}=\left(3^{2}-1^{2}\right)+\left(4^{2}-2^{2}\right)+\ldots \ldots \ldots \ldots$
$\mathrm{S}_{\mathrm{n}}=2(1+2+3+\ldots \ldots+4 \mathrm{n})=\frac{2(4 n)(4 \mathrm{n}+1)}{2}$
$\mathrm{S}_{\mathrm{n}}=4 \mathrm{n}(4 \mathrm{n}+1)$
$\mathrm{S}_{\mathrm{n}}=4 \mathrm{n}(4 \mathrm{n}+1)=1056$ is possible when $\mathrm{n}=8$
$4 n(4 n+1)=1088$ not possible
$4 n(4 n+1)=1120$ not possible
$4 n(4 n+1)=1332$ possible when $n=9$
Q. A pack contains n cards numbered from 1 to n. Two consecutive numbered cards are removed from the pack and the sum of the numbers on the remaining cards is 1224. If the smaller to the numbers on the removed cards is k, then k – 20 =
[JEE-Advanced 2013, 4, (–1)]
Ans. 5
When 1 and 2 are removed from numbers 1 to n then we get maximum possible sum of remaining numbers and when n –1,n are removed then get minimum possible sum of remaining numbers.


Q. Let a, b, c be positive integers such that $\frac{b}{a}$ is an integer. If $a, b, c$ are in geometric progression and the arithmetic mean of $a, b, c$ is $b+2,$ then the value of $\frac{a^{2}+a-14}{a+1}$ is
[JEE(Advanced)-2014, 3]
Ans. 4


Q. Let $b_{i}>1$ for $i=1,2, \ldots \ldots, 101 .$ Suppose $\log _{e} b_{1}, \log _{e} b_{2}, \ldots \ldots, \log b_{10}$ are in Arithmetic Progression (A.P.) with the common difference log $2 .$ Suppose $a_{1}, a_{2}, \ldots . ., a_{101}$ are in A.P. such that $a_{1}=$ $b_{1}$ and $a_{51}=b_{51}$. If $t=b_{1}+b_{2}+\ldots . .+b_{51}$ and $s=a_{1}+a_{2}+\ldots . .+a_{51}$ then
(A) $\mathrm{s}>\mathrm{t}$ and $\mathrm{a}_{101}>\mathrm{b}_{101}$
(B) $\mathrm{s}>\mathrm{t}$ and $\mathrm{a}_{101}<\mathrm{b}_{101}$
(C) $\mathrm{s}<\mathrm{t}$ and $\mathrm{a}_{101}>\mathrm{b}_{101}$
(D) $\mathrm{s}<\mathrm{t}$ and $\mathrm{a}_{101}<\mathrm{b}_{101}$
[JEE(Advanced)-2016]
Ans. B






Q. The sides of the right angled triangle are in arithmetic progression. If the triangle has area 24, then what is the length of its smallest side ?
[JEE(Advanced)-2017]
Ans. 6
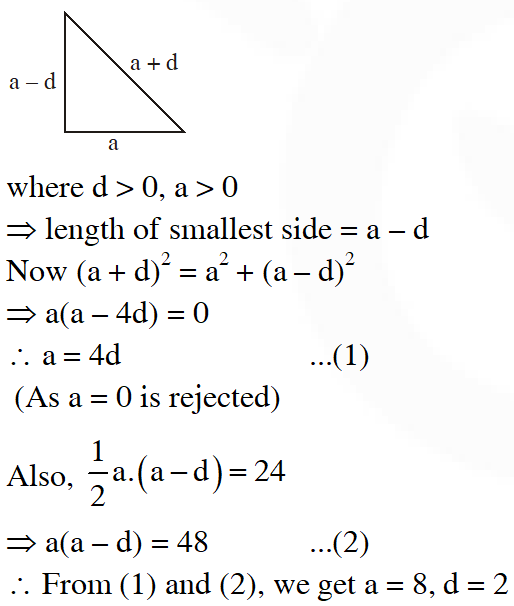

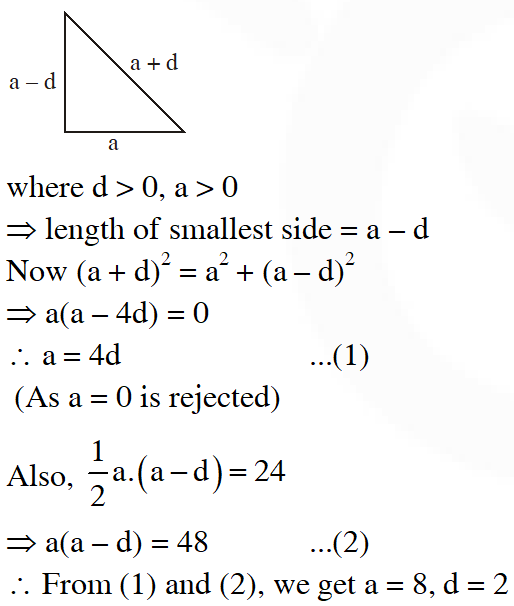
Q. Let $X$ be the set consisting of the first 2018 terms of the arithmetic progression $1,6,11, \ldots .$ , and $Y$ be the set consisting of the first 2018 terms of the arithmetic progression $9,16,23,$ $\ldots \ldots$ Then, the number of elements in the set $X \cup Y$ is
[JEE(Advanced)-2018]
Ans. 3748