Sequence-Series - JEE Main Previous Year Question with Solutions
Sequence and Series questions in JEE Main primarily test Arithmetic Progressions (AP), Geometric Progressions (GP), and Arithmetico-Geometric Progressions (AGP). NTA has asked 1–2 questions per paper from this chapter. Students who master sum formulas, common difference/ratio properties, and AM–GM inequalities typically solve these questions within 2 minutes.
JEE Main Previous Year Question of Math with Solutions are available at eSaral. Practicing JEE Main Previous Year Papers Questions of mathematics will help the JEE aspirants in realizing the question pattern as well as help in analyzing weak & strong areas.eSaral helps the students in clearing and understanding each topic in a better way. eSaral is providing complete chapter-wise notes of Class 11th and 12th both for all subjects.Besides this, eSaral also offers NCERT Solutions, Previous year questions for JEE Main and Advance, Practice questions, Test Series for JEE Main, JEE Advanced and NEET, Important questions of Physics, Chemistry, Math, and Biology and many more.Download eSaral app for free study material and video tutorials.
Q. The sum to infinity of the series $1+\frac{2}{3}+\frac{6}{3^{2}}+\frac{10}{3^{3}}+\frac{14}{3^{4}}+\ldots .$ is :- (1) 4 (2) 6 (3) 2 (4) 3[AIEEE-2009]
Ans. (4)
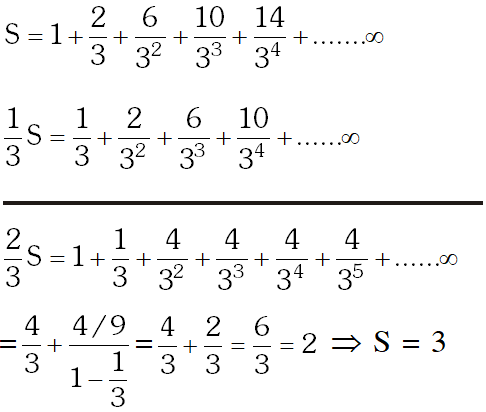
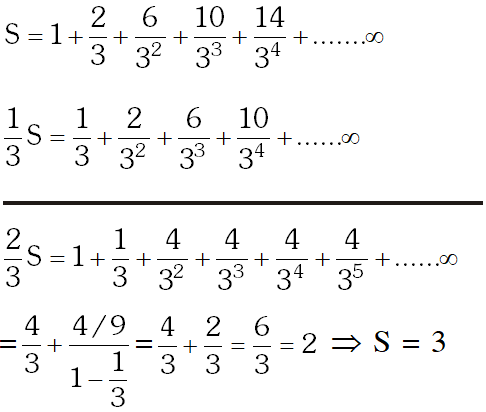
Q. A person is to count 4500 currency notes. Let a denote the number of notes he counts in the $\mathrm{n}^{\mathrm{th}}$ minute. If $\mathrm{a}_{1}=\mathrm{a}_{2}=\ldots=\mathrm{a}_{10}=150$ and $\mathrm{a}_{10} \mathrm{a}_{11}, \ldots$ are in an AP with common difference - $2,$ then the time taken by him to count all notes is :- (1) 24 minutes (2) 34 minutes (3) 125 minutes (4) 135 minutes[AIEEE-2010]
Ans. (2)
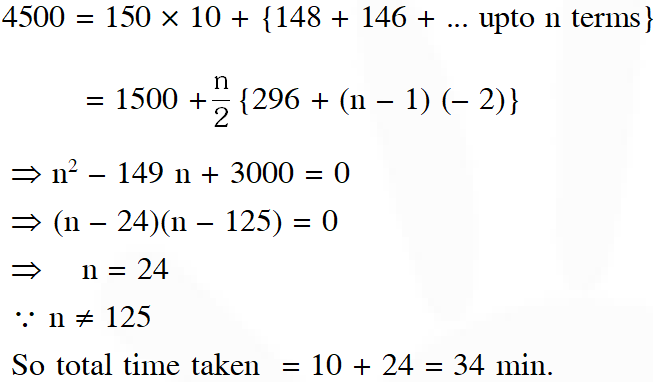
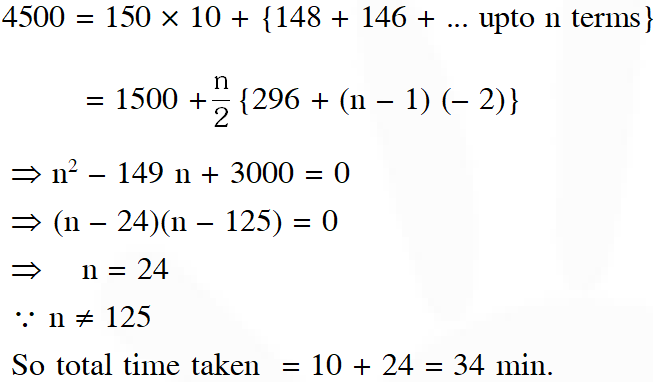
Q. A man saves Rs. 200 in each of the first three months of his service. In each of the subsequent months his saving increases by Rs. 40 more the saving of immediately previous month. His total saving from the start of service will be Rs. 11040 after :- (1) 20 months (2) 21 months (3) 18 months (4) 19 months[AIEEE-2011]
Ans. (2) Saving after first 3 month $=600$$600+\left\{\frac{240+280+\ldots .}{\text { let } n \text { month }}\right\}=11040$$| 240+280+\ldots . .$ n terms $|=10440$n/2 $[480+\ldots . . . \text { n terms }]=10440$n/2 $[480+(n-1) 40]=10440$n $\{440+40 n\}=20880$$\mathrm{n}^{2}+11 \mathrm{n}-522=0$$\mathrm{n}=18,-29 \quad(-29 \text { rejected })$Total months $=\mathrm{n}+3$18 $+3=21$ Months
Q. Let $a_{n}$ be the $n^{\text {th }}$ term of an A.P. If $\sum_{r=1}^{100} a_{2 r}=\alpha$ and $\sum_{r=1}^{100} a_{2 r-1}=\beta,$ then the common difference of the A.P. is : (1) $\frac{\alpha-\beta}{200}$(2) $\alpha-\beta$(3) $\frac{\alpha-\beta}{100}$(4) $\beta-\alpha$[AIEEE-2011]
Ans. (3)
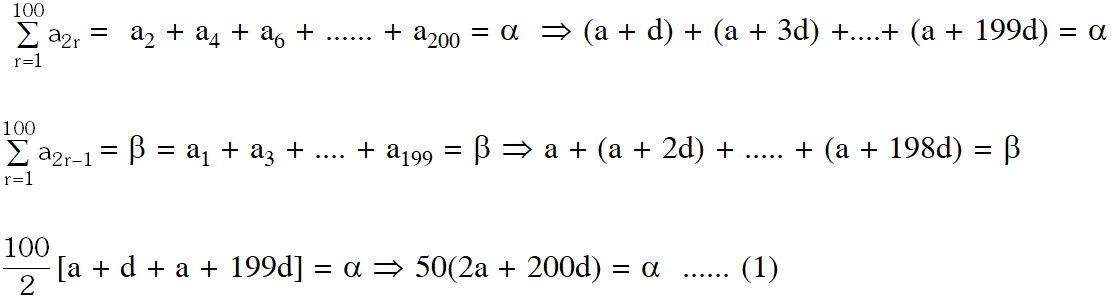
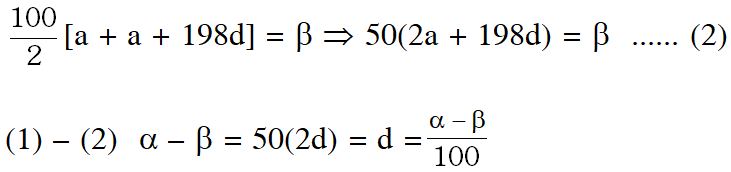
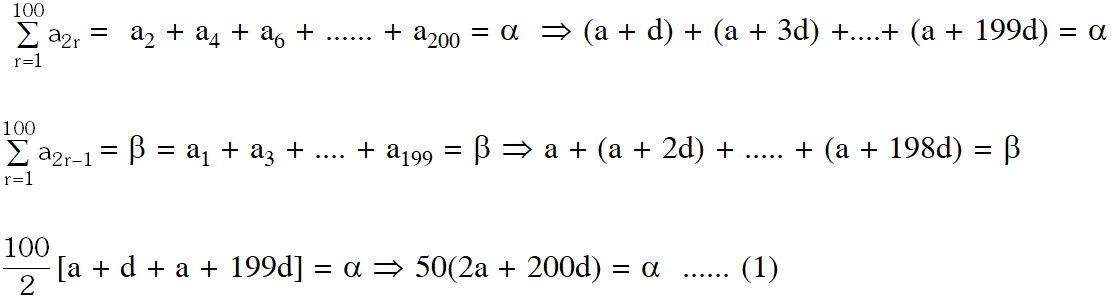
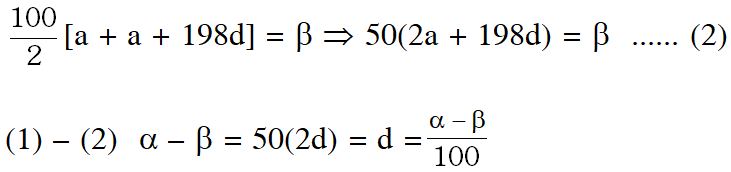
Q. Statement-1: The sum of the series $1+(1+2+4)+(4+6+9)+(9+12+16)$ $\quad+\ldots \ldots+(361+380+400)$ is $8000 .$Statement-2: $\sum_{\mathrm{k}=1}^{\mathrm{n}}\left(\mathrm{k}^{3}-(\mathrm{k}-1)^{3}\right)=\mathrm{n}^{3},$ for any natural number $\mathrm{n}$(1) Statement-1 is true, Statement-2 is false.(2) Statement- 1 is false, Statement- 2 is true.(3) Statement- 1 is true, Statement-2 is true ; Statement-2 is a correct explanation forStatement-1.(4) Statement-1 is true, Statement-2 is true; Statement-2 is not a correct explanation forStatement- - $1 .$[AIEEE-2012]
Ans. (4) Statement-1:$\left(1^{3}-0^{3}\right)+\left(2^{3}-1^{3}\right)+\left(3^{3}-2^{3}\right)+\ldots+\left(20^{3}-19^{3}\right)=20^{3}=8000$ Statement-l is true.Statement-2:$\sum_{k=1}^{n} k^{3}-(k-1)^{3}=\left(1^{3}-0^{3}\right)+\left(2^{3}-1^{3}\right)+\left(3^{3}-2^{3}\right)+\ldots . n^{3}+(n-1)^{3}=n^{3}$Statement-2 is true and Statement-2 is a correct explanation of Statement- $1 .$
Q. If 100 times the 100th term of an A.P. with non-zero common difference equals the 50 times its 50th term, then the 150th term of this A.P. is :(1) zero (2) –150 (3) 150 times its 50th term (4) 150[AIEEE-2012]
Ans. (1)
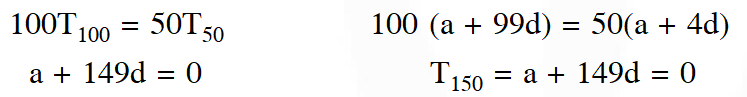
Q. The sum of first 20 terms of the sequence 0.7, 0.77, 0.777, ......, is : (1) $\frac{7}{81}\left(179-10^{-20}\right)$(2) $\frac{7}{9}\left(99-10^{-20}\right)$(3) $\frac{7}{81}\left(179+10^{-20}\right)$(4) $\frac{7}{9}\left(99-10^{-20}\right)$[JEE(Main)-2013]
Ans. (3) $S=\frac{7}{10}+\frac{77}{100}+\frac{777}{1000}+\ldots \ldots \quad S=\frac{7}{9}\left\{\frac{10-1}{10}+\frac{100-1}{100}+\frac{1000-1}{1000}+\ldots\right\}$$=\frac{7}{9}\left\{20-\frac{1}{10}\left(\frac{1-10^{-20}}{9 / 10}\right)\right\}=\frac{7}{9}\left\{20-\frac{1}{9}\left(1-10^{-20}\right)\right\}=\frac{7}{81}\left(179+10^{-20}\right)$
Q. Let $\alpha$ and $\beta$ be the roots of equation $\mathrm{px}^{2}+\mathrm{qx}+\mathrm{r}=0, \mathrm{p} \neq 0 .$ If $\mathrm{p}, \mathrm{q}, \mathrm{r}$ are in A.P. and $\frac{1}{\alpha}+\frac{1}{\beta}=4,$ then the value of $|\alpha-\beta|$ is: (1) $\frac{\sqrt{61}}{9}$(2) $\frac{2 \sqrt{17}}{9}$(3) $\frac{\sqrt{34}}{9}$(4) $\frac{2 \sqrt{13}}{9}$[JEE(Main)-2014]
Ans. (4) $\frac{\alpha+\beta}{\alpha \beta}=4=-\frac{q}{r} \Rightarrow q=-4 r$$\because p, q \& r$ are in A.P $2 q=p+r$$\Rightarrow \quad-8 r=p+r \Rightarrow p=-9 r$$|\alpha-\beta|=\sqrt{(\alpha+\beta)^{2}-4 \alpha \beta}=\sqrt{\frac{16 r^{2}+36 r^{2}}{p^{2}}}=\sqrt{\frac{52 r^{2}}{p^{2}}}=\sqrt{\frac{52}{81}}=\frac{2 \sqrt{13}}{9}$
Q. Three positive numbers form an increasing G.P. If the middle term in this G.P. is doubled, the new numbers are in A.P. Then the common ratio of the G.P. is : (1) $\sqrt{2}+\sqrt{3}$(2) $3+\sqrt{2}$(3) $2-\sqrt{3}$(4) $2+\sqrt{3}$[JEE(Main)-2014]
Ans. (4) Let a, ar, ar $^{2}$ are in G.P$\therefore \quad$ a, 2 ar, $\operatorname{ar}^{2}$ are in AP$\Rightarrow \quad 4$ ar $=a+a r^{2}$$\Rightarrow \quad r^{2}-4 r+1=0$$\Rightarrow r=2+\sqrt{3}, 2-\sqrt{3}$since GP is an increasing G.P$\Rightarrow r=2+\sqrt{3}$
Q. If $(10)^{9}+2(11)^{1}(10)^{8}+3(11)^{2}(10)^{7}+\ldots \ldots+10(11)^{9}=\mathrm{k}(10)^{9},$ then $\mathrm{k}$ is equal to : (1) $\frac{121}{10}$(2) $\frac{441}{100}$(3) 100(4) 110[JEE(Main)-2014]
Q. If $\mathrm{m}$ is the A.M. of two distinct real numbers 1 and $\mathrm{n}(1, \mathrm{n}>1)$ and $\mathrm{G}_{1}, \mathrm{G}_{2}$ and $\mathrm{G}_{3}$ are three geometric means between 1 and $\mathrm{n}$, then $\mathrm{G}_{1}^{4}+2 \mathrm{G}_{2}^{4}+\mathrm{G}_{3}^{4}$ equals – (1) $4 \operatorname{lmn}^{2}$(2) $41^{2} \mathrm{m}^{2} \mathrm{n}^{2}$(3) $4 \mathrm{l}^{2} \mathrm{mn}$(4) $4 \ln ^{2} n$[JEE(Main)-2015]
Ans. (4) $\ell, \mathrm{G}_{1}, \mathrm{G}_{2}, \mathrm{G}_{3}, \mathrm{n}$ in G.P.Let $\mathrm{r}$ be the common ratio $\Rightarrow \mathrm{r}^{4}=\frac{\mathrm{n}}{\ell}$Here $\mathrm{G}_{1}^{4}+2 \mathrm{G}_{2}^{4}+\mathrm{G}_{3}^{4}=(\ell \mathrm{r})^{4}+2\left(\ell \mathrm{r}^{2}\right)^{4}+\left(\ell \mathrm{r}^{3}\right)^{4}=\mathrm{n} \ell\left[\ell^{2}+2 \ell \mathrm{n}+\mathrm{n}^{2}\right]=\mathrm{n} \ell(\ell+\mathrm{n})^{2}=\mathrm{n} \ell 4 \mathrm{m}^{2}$$=4 \mathrm{m}^{2} \mathrm{n} \ell \quad(\because 2 \mathrm{m}=\mathrm{n}+\ell)$
Q. If the 2nd, 5th and 9th terms of a non-constant A.P. are in G.P., then the common ratio of this G.P.is ( 1)$\frac{7}{4}$(2) $\frac{8}{5}$(3) $\frac{4}{3}$(4) 1[JEE(Main)-2016]
Ans. (3) Let 'a' be the first term and d be the common difference$2^{\text {nd }} \operatorname{term}=a+d, 5^{\text {th }} \operatorname{term}=a+4 d$,9th term $=4+8 d$$\therefore$ Common ratio $=\frac{a+4 d}{a+d}=\frac{a+8 d}{a+4 d}=\frac{4 d}{3 d}=\frac{4}{3}$
Q. If the sum of the first ten terms of the series $\left(1 \frac{3}{5}\right)^{2}+\left(2 \frac{2}{5}\right)^{2}+\left(3 \frac{1}{5}\right)^{2}+4^{2}+\left(4 \frac{4}{5}\right)^{2}+\ldots,$ is $\frac{16}{5} \mathrm{m}$, then $\mathrm{m}$ is equal to :- (1) 99 (2) 102 (3) 101 (4) 100[JEE(Main)-2016]
Ans. (3) Given series is$\mathrm{S}=\frac{8^{2}}{5^{2}}+\frac{12^{2}}{5^{2}}+\frac{16^{2}}{5^{2}}+\ldots 10 \mathrm{terms}$$=\frac{4^{2}}{5^{2}}\left(2^{2}+3^{2}+4^{2}+\ldots .10 \mathrm{terms}\right)$$=\frac{16}{25}\left(\frac{11.12 .23}{6}-1\right)=\frac{16}{25} \times 505$$\therefore \mathrm{m}=101$
Q. If, for a positive integer n, the quadratic equation, $\mathrm{x}(\mathrm{x}+1)+(\mathrm{x}+1)(\mathrm{x}+2)+\ldots \ldots+(\mathrm{x}+\overline{\mathrm{n}-1})(\mathrm{x}+\mathrm{n})$= 10n has two consecutive integral solutions, then n is equal to :(1) 11 (2) 12 (3) 9 (4) 10[JEE(Main)-2017]
Ans. (1) We have$\sum_{\mathrm{r}=1}^{\mathrm{n}}(\mathrm{x}+\mathrm{r}-1)(\mathrm{x}+\mathrm{r})=10 \mathrm{n}$$\Rightarrow \sum_{\mathrm{r}=1}^{\mathrm{n}}\left(\mathrm{x}^{2}+(2 \mathrm{r}-1) \mathrm{x}+\left(\mathrm{r}^{2}-\mathrm{r}\right)\right)=10 \mathrm{n}$$\therefore$ On solving, we get
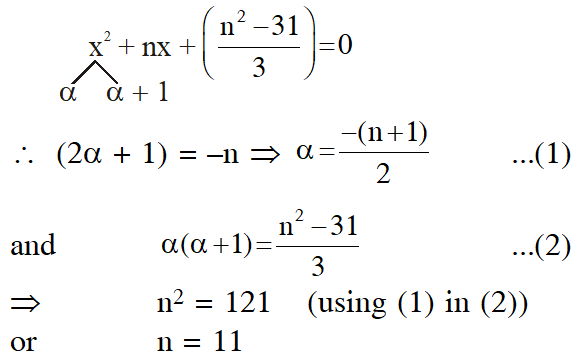
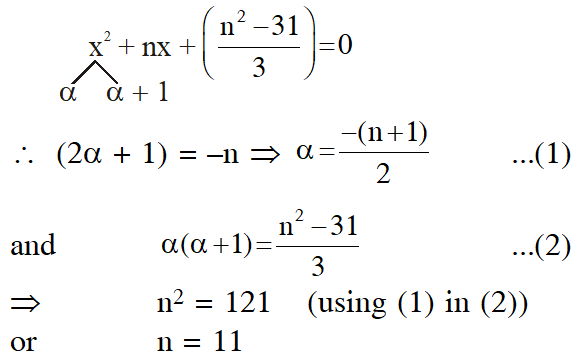
Q. For any three positive real numbers a, b and $c, 9\left(25 a^{2}+b^{2}\right)+25\left(c^{2}-3 a c\right)=15 b(3 a+c)$ Then : (1) a, b and c are in G.P.(2) b, c and a are in G.P.(3) b, c and a are in A.P.(4) a, b and c are in A.P.[JEE(Main)-2017]
Ans. (3) $(15 a)^{2}+(3 b)^{2}+(5 c)^{2}-(15 a)(5 c)-(15 a)(3 b)-(3 b)(5 c)=0$$\frac{1}{2}\left[(15 a-3 b)^{2}+(3 b-5 c)^{2}+(5 c-15 a)^{2}\right]=0$it is possible when $15 a=3 b=5 c$$\therefore b=\frac{5 c}{3}, a=\frac{c}{3}$$a+b=2 c$$\Rightarrow b, c, a$ in A.P.
Q. Let $a, b, c \in R .$ If $f(x)=a x^{2}+b x+c$ is such that $a+b+c=3$ and $f(x+y)=f(x)+f(y)+$ $\mathrm{xy}, \forall \mathrm{x}, \mathrm{y} \in \mathrm{R},$ then $\sum_{\mathrm{n}=1}^{10} \mathrm{f}(\mathrm{n})$ is equal to : (1) 255 (2) 330 (3) 165 (4) 190[JEE(Main)-2017]
Ans. (2)
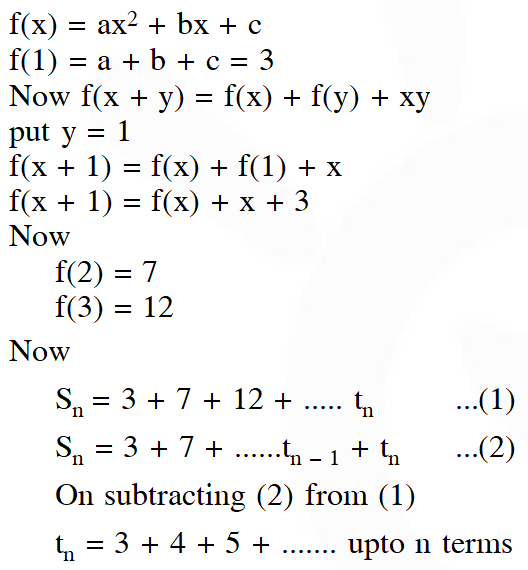
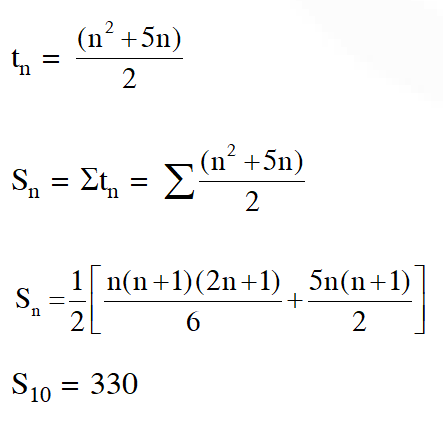
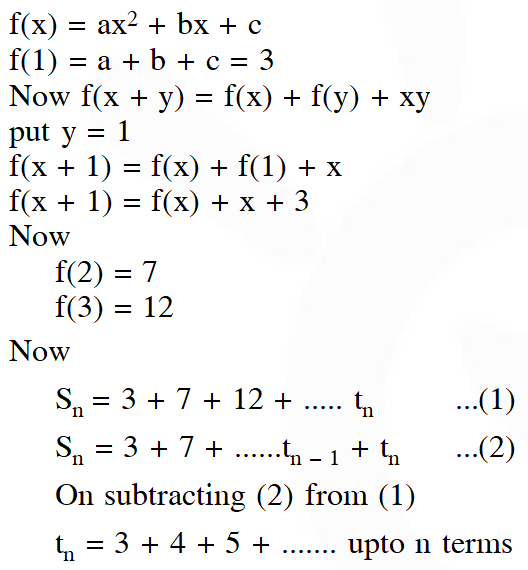
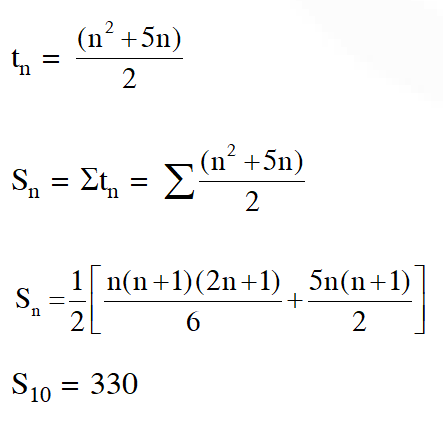
Q. Let $a_{1}, a_{2}, a_{3}, \ldots ., a_{49}$ be in A.P. such that $\sum_{\mathrm{k}=0}^{12} \mathrm{a}_{4 \mathrm{k}+1}$ $=416$ and $a_{9}+a_{43}=66 .$ If $a_{1}^{2}+a_{2}^{2}+\ldots \ldots+a_{17}^{2}$ = 140m, then m is equal to- (1) 68 (2) 34 (3) 33 (4) 66[JEE(Main)-2018]
Ans. (2)
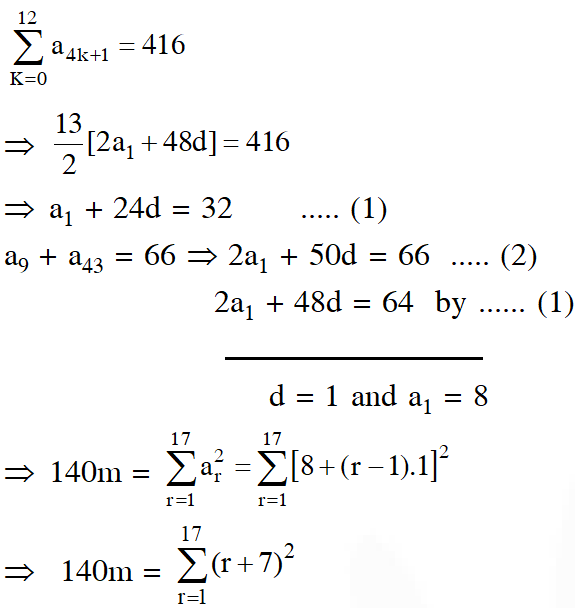
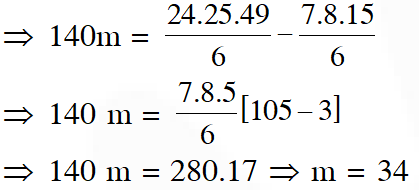
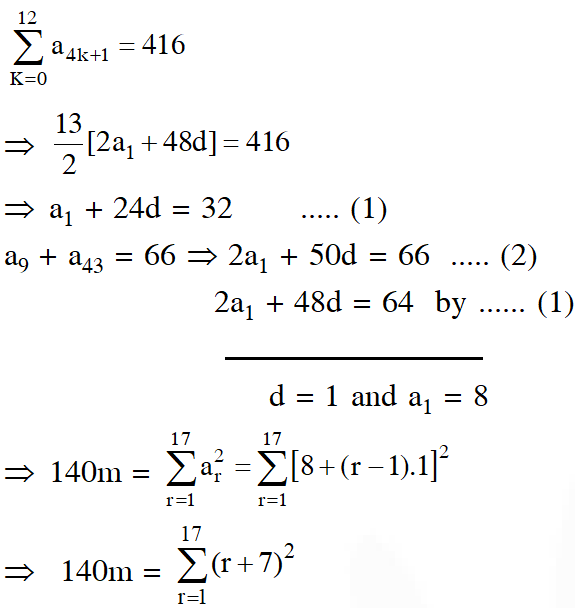
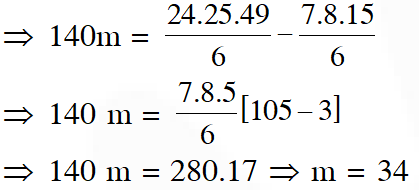
Q. Let A be the sum of the first 20 terms and B be the sum of the first 40 terms of the series $1^{2}+2 \cdot 2^{2}+3^{2}+2 \cdot 4^{2}+5^{2}+2 \cdot 6^{2}+\ldots \ldots \ldots \quad$ If $\mathrm{B}-2 \mathrm{A}=100 \lambda,$ then $\lambda$ is equal to : (1) 248 (2) 464 (3) 496 (4) 232[JEE(Main)-2018]
Ans. (1)
Share Blog
Share via...
Or copy link
Frequently Asked Questions
Find answers to common questions.
Can I solve Sequence and Series questions without practising previous year papers?
Technically yes, but practically no. The JEE Main question style has specific patterns — disguised APs, functional equations that reduce to series, and statements about means — that only become recognisable through repeated exposure to past papers. Students who skip previous year questions consistently underperform in this chapter relative to their conceptual preparation level
What formulas must be memorised for Sequence and Series JEE Main?
Essential formulas: sum of n terms of AP (Sₙ = n/2 [2a + (n−1)d]), sum of GP (Sₙ = a(rⁿ−1)/(r−1)), sum to infinity of GP (a/(1−r) for |r|<1), sum of squares (Σn² = n(n+1)(2n+1)/6), sum of cubes (Σn³ = [n(n+1)/2]²), and the AGP standard result. These seven cover 90% of JEE Main questions on this topic.
What is the best way to study Sequence and Series for JEE Main?
Start with NCERT Class 11 theory to solidify definitions. Then solve the previous year questions on this page year-by-year, not topic-by-topic. This trains pattern recognition. Finally, time yourself: each Sequence and Series question in JEE Main should take under 2.5 minutes. If it is taking longer, you need more formula fluency, not more theory.
Is Sequence and Series asked in JEE Advanced too?
Yes. JEE Advanced asks more complex forms — multi-variable progressions, inequalities involving AM–GM–HM, and integer-type problems requiring exact sums. Clearing JEE Main-level questions with full understanding (not just memorised steps) is the right foundation for JEE Advanced preparation.
Which sub-topics of Sequence and Series are most important for JEE Main?
Arithmetic Progressions (AP) are the most frequently tested sub-topic, appearing in 7 of the 18 questions on this page alone. Geometric Progressions (GP) come second. Students should also prepare AGP (Arithmetico-Geometric Progressions) and telescoping sums, as these appear as medium-to-hard questions that can differentiate ranks.
How many questions come from Sequence and Series in JEE Main?
JEE Main typically asks 1–2 questions from Sequence and Series per session. With NTA conducting multiple sessions per year, this chapter can contribute 4–6 questions across the full exam cycle. It is a medium-weightage but highly scoring topic because the question types repeat predictably across years
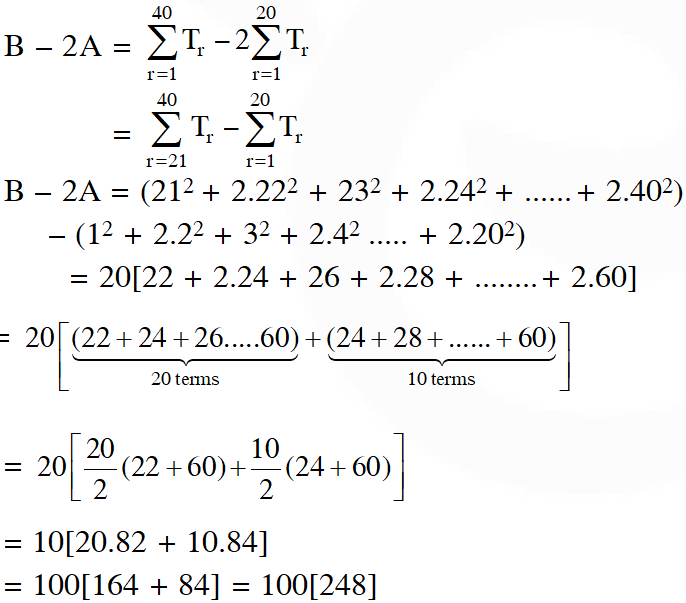
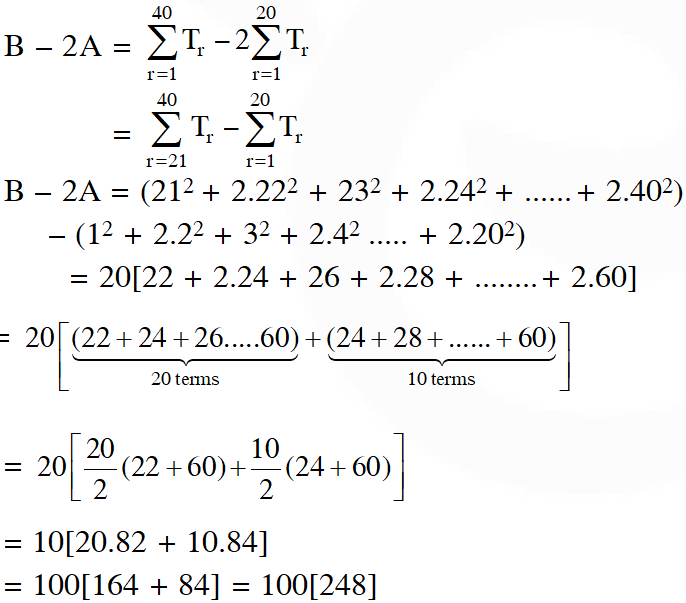
Comments
Sampreet
Nov. 12, 2025, 6:35 a.m.
Very nice it has helped me alot thsnk you
Payal
Oct. 20, 2025, 6:35 a.m.
Thanku
Alok kumar
Oct. 26, 2024, 6:35 a.m.
Please add question of 2019-20-21-22-23-24
Srushti More
Nov. 8, 2024, 6:35 a.m.
Hii
Srushti More
Nov. 8, 2024, 6:35 a.m.
Please add question 2020 21 22 23 24
Arpit Giri
Oct. 26, 2024, 6:35 a.m.
Please add question of 2019-20-21-22-23-24
Suraj kumar
Jan. 22, 2024, 6:35 a.m.
Last questions solution is not explain. But thank you for questions.
Kritika
Aug. 22, 2023, 6:54 p.m.
Please add questions of 2019-20-21-22-23
Raja
March 11, 2023, 7:29 p.m.
In the last question,the solution is inaccurate.
Raja
March 11, 2023, 7:29 p.m.
In the last second
Aashna Khurana
July 23, 2022, 10:40 a.m.
Thank u E saral for providing these questions really thank u
Vijaydeep
March 16, 2022, 5:48 p.m.
Thank you 🙏
Kalmkaar raftaar
Jan. 29, 2022, 1:24 p.m.
Thnk. You eSaral
Mukkamala sumanth
Aug. 23, 2021, 3:36 p.m.
Thankuu broo
Heavy driver
June 6, 2021, 8:59 p.m.
Nice
Bhuvana
March 8, 2021, 7:04 p.m.
Update 2019,2020 questions also
sanobar
Feb. 17, 2021, 1:49 p.m.
but I am still trying . ................mission_______LETS KILL JEE %%%%%%%%
sanobar
Feb. 17, 2021, 1:45 p.m.
its too hard doode
swap
Dec. 16, 2020, 4:56 p.m.
cannot open solutions tho
swap
Dec. 16, 2020, 4:56 p.m.
nice
Amaan
Dec. 7, 2020, 12:02 a.m.
Subscription liya hai bhai eska?
Monu
Dec. 5, 2020, 12:30 a.m.
Nice helps a lot THANKS TO THE WHOLE eSARAL TEAM for their efforts
cristiano ronaldo
Nov. 26, 2020, 12:08 a.m.
where are 2020 and 2019 questions
Anonymous
Nov. 19, 2020, 5:02 p.m.
Now I can!
Anonymous
Nov. 19, 2020, 4:58 p.m.
Can't load solutions!
Divyanshu
Oct. 19, 2020, 9:42 p.m.
Superb esaral ne jee or neet ke bachoo ke liye joo chapterwise privi previous year ke liye question ek jgh collect krke rkh rakhe h ye bht useful h superb esaral apne students ka kaam kr saral kr diya h
prashant chauhan
Sept. 29, 2020, 8:33 p.m.
nice
Bamniya Bro
Sept. 26, 2020, 12:16 p.m.
Excellent job
pallavi
Sept. 18, 2020, 7:28 p.m.
good
Monu
Sept. 16, 2020, 10:46 a.m.
It's helpful
Madhu
Sept. 12, 2020, 7:12 p.m.
Gogious thanks
Manoj
Sept. 3, 2020, 8:36 a.m.
Ok
Goodboi
Sept. 1, 2020, 6:01 p.m.
Please Update this list and add 2019 and 2020 Questions also .
