JEE Main Previous Year Question of Math with Solutions are available at eSaral. Practicing JEE Main Previous Year Papers Questions of mathematics will help the JEE aspirants in realizing the question pattern as well as help in analyzing weak & strong areas.
eSaral helps the students in clearing and understanding each topic in a better way. eSaral is providing complete chapter-wise notes of Class 11th and 12th both for all subjects.
Besides this, eSaral also offers NCERT Solutions, Previous year questions for JEE Main and Advance, Practice questions, Test Series for JEE Main, JEE Advanced and NEET, Important questions of Physics, Chemistry, Math, and Biology and many more.
Download eSaral app for free study material and video tutorials.
Q. If $\mathrm{A}, \mathrm{B}$ and $\mathrm{C}$ are three sets such that $\mathrm{A} \cap \mathrm{B}=\mathrm{A} \cap \mathrm{C}$ and $\mathrm{A} \cup \mathrm{B}=\mathrm{A} \cup \mathrm{C},$ then :-
(1) B = C
$(2) \mathrm{A} \cap \mathrm{B}=\phi$
(3) A = B
(4) A = C
[AIEEE- 2009]
Ans. (1)
$\mathrm{n}(\mathrm{A})=3, \mathrm{n}(\mathrm{B})=6, \mathrm{n}(\mathrm{A} \cap \mathrm{B})=3(\text { maximum })$
so $\mathrm{n}(\mathrm{A} \cup \mathrm{B})=\mathrm{n}(\mathrm{A})+\mathrm{n}(\mathrm{B})-\mathrm{n}(\mathrm{A} \cap \mathrm{B})$
$3+6-3$
$\mathrm{n}(\mathrm{A} \cup \mathrm{B})=6$
so minimum no of elements in $\mathrm{A} \cup \mathrm{B}$ is $6 .$
Q. Two sets A and B are as under
$\mathrm{A}=\{(\mathrm{a}, \mathrm{b}) \in \mathrm{R} \times \mathrm{R}:|\mathrm{a}-5|<1 \text { and }|\mathrm{b}-5|<1\}$
$\mathrm{B}=\left\{(\mathrm{a}, \mathrm{b}) \in \mathrm{R} \times \mathrm{R}: 4(\mathrm{a}-6)^{2}+9(\mathrm{b}-5)^{2} \leq 36\right\} .$ Then
(1) $\mathrm{A} \subset \mathrm{B}$
(2) $\mathrm{A} \cap \mathrm{B}=\phi$ (an empty set)
(3) neither $\mathrm{A} \subset \mathrm{B}$ nor $\mathrm{B} \subset \mathrm{A}$
(4) $\mathrm{B} \subset \mathrm{A}$
[JEE-MAINS-2018]
Ans. (1)
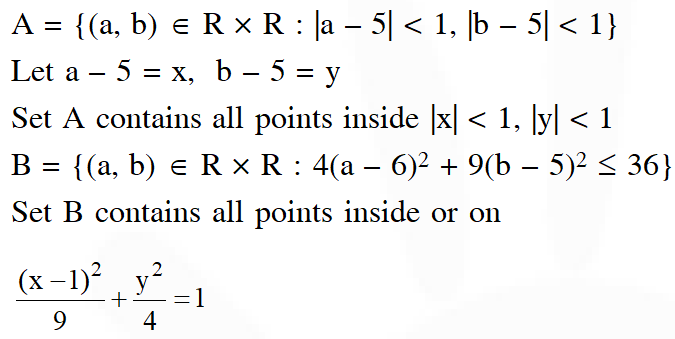
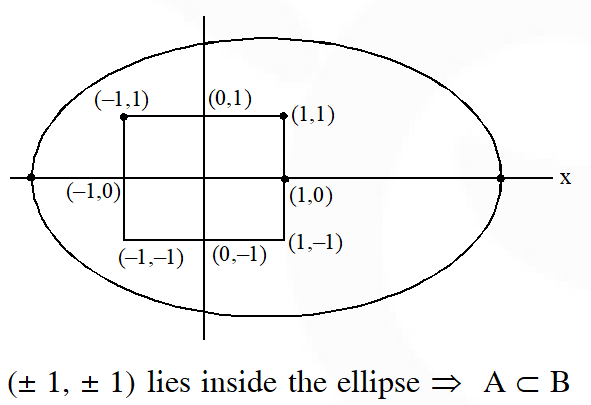
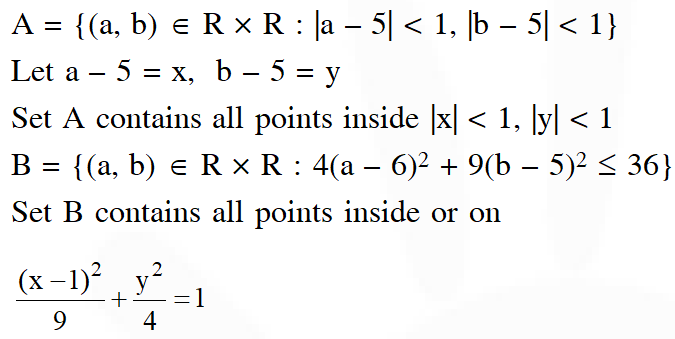
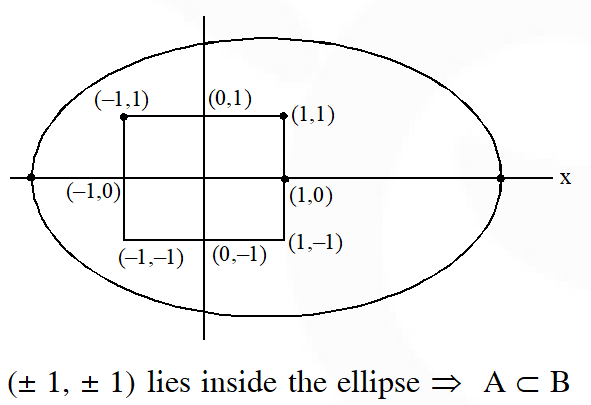
Q. Let $\mathrm{S}=\{\mathrm{x} \in \mathrm{R}: \mathrm{x} \geq 0 \text { and } 2|\sqrt{\mathrm{x}}-3|+\sqrt{\mathrm{x}}(\sqrt{\mathrm{x}}-6)+6=0\} .$ Then $\mathrm{S}:$
(1) contains exactly one element.
(2) contains exactly two elements.
(3) contains exactly four elements.
(4) is an empty set.
[JEE-MAINS-2018]
Ans. (2)
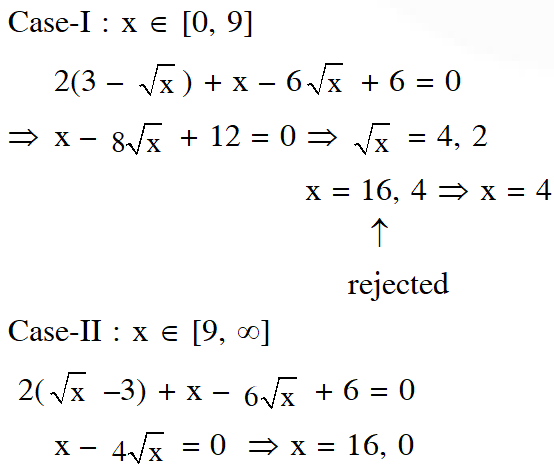
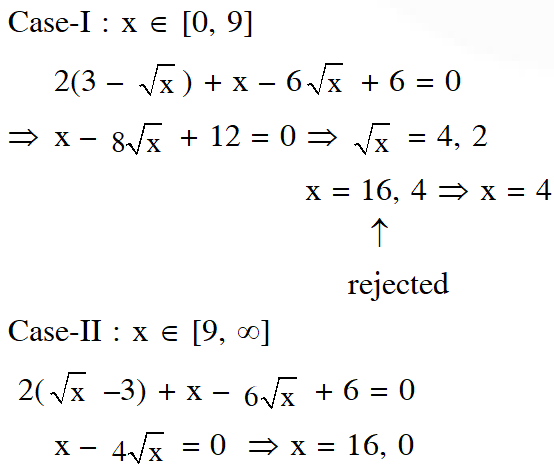
Comments
online pharmacies in usa
Oct. 25, 2023, 7:03 a.m.
Write more, thats all I have to say. Literally, it seems as though you relied on the video to make your point. You definitely know what youre talking about, why throw away your intelligence on just posting videos to your blog when you could be giving us something informative to read?
Nikhil Kumar
Sept. 23, 2021, 8:09 p.m.
Provide more number of questions and give correct solutions of each regarding questions.
Op lol
July 23, 2021, 6:06 p.m.
E sala become rotten u provide more no of
Question and do their best solution
But yo do wrong solution
Manas
Nov. 24, 2020, 11:34 a.m.
Not giving sol correct that problem rather than that no problem good
