Snell's law of refraction - Ray Optics, Physics - eSaral

Hey, do you want to learn about Snell's law of refraction? If yes. Then keep reading.

Snell’s Law:

For any two media and for the light of a given wavelength, the ratio of the sine of the angle of incidence to the sine of the angle of refraction is a constant.

$\frac{\operatorname{Sin} \mathrm{i}}{\operatorname{Sin} \mathrm{r}}=$ constant,

Where i = incidence angle
r = refraction angle.

The incident ray, the refracted ray, and the normal at the incident point all lie in the same plane. Frequency (and hence the color) and phase do not change (while wavelength and velocity changes)

Application of Snell’s Law:

1. When light passes from rarer to denser medium it bends toward the normal. Using Snell’s Law $\mu_{1} \sin \theta_{1}=\mu_{2} \sin \theta_{2}$ 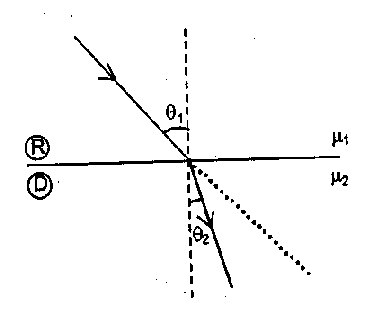$\frac{\sin \theta_{1}}{\sin \theta_{2}}=\frac{\mu_{2}}{\mu_{1}}$ Thus If $\mu_{2}>\mu_{1}$ then $\theta_{2}<\theta_{1}$
   
   
2. When light passes from denser to rarer medium it bends away from the normal. From Snell’s law
   
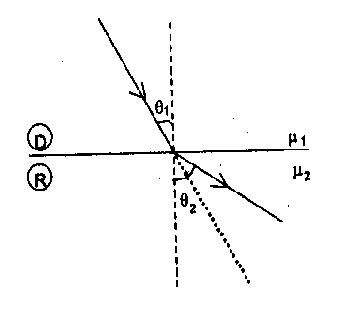
   $\frac{\sin \theta_{1}}{\sin \theta_{2}}=\frac{\mu_{2}}{\mu_{1}}$ Thus If $\mu_{2}<\mu_{1}$ then $\theta_{2}>\theta_{1}$
   
   
3. When light propagates through a series of layers of different medium, then according to Snell’s law
   
   
   
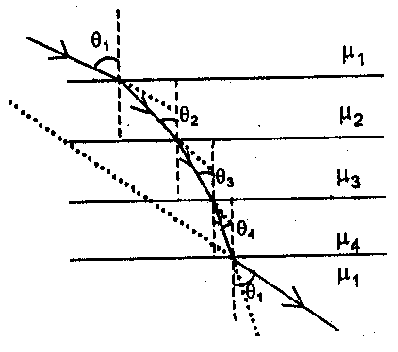
   $\mu_{1} \sin \theta,=\mu_{2} \sin \theta_{2}=\mu_{3} \sin \theta_{3}=\ldots \ldots \ldots .=$ constant
   
   
4. Conditions of no refraction
   
   (a) If light is incident normally on a boundary i.e., $\angle \mathrm{i}=0^{\circ}$ Then from Snell’s law

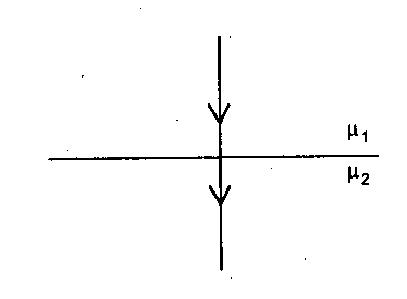$\mu_{1} \sin 0=\mu_{2} \sin r$

$\sin r=0$ i.e. $\angle \mathrm{r}=0$

i.e., light passes undeviated from the boundary.

(so boundary will be invisible)

(b) If the refractive indices of two media are equal i.e., if, 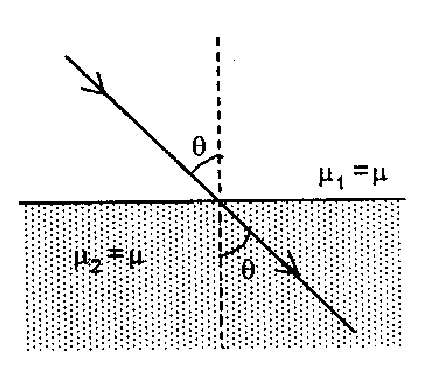$\mu_{1}=\mu_{2}=\mu$

Then from Snell’s law

$\mu_{1} \sin \mathrm{i}=\mu \sin r$

$\Rightarrow \angle \mathrm{i}=\angle \mathrm{r}$ i.e.

ray passes undeviated from the boundary with $\angle \mathrm{i}=\angle \mathrm{r} \neq 0$ and boundary will not be visible.

This is also why a transparent solid is invisible in a liquid if $\mu_{s}=\mu_{L}$

5.  Relation between object and image distance :

An object O placed in first medium (refractive index $\mu_{1}$) is viewed from the second medium (refractive index $\mu_{2}$). Then the image distance $\mathrm{d}_{\mathrm{AP}}$ and the object

distance $\mathrm{d}_{\mathrm{AC}}$ are related as

$\mathrm{d}_{\mathrm{AP}}=\left(\frac{\mu_{2}}{\mu_{1}}\right) \mathrm{d}_{\mathrm{AC}}$

(a.)  If $\mu_{2}>\mu_{1}$, i.e., when the object is observed from a denser medium, it appears to be farther away from the interface,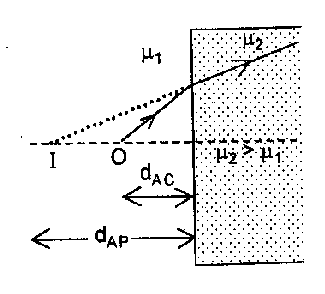 i.e. $\mathrm{d}_{\mathrm{AP}}>\mathrm{d}_{\mathrm{AC}}$

(b.) If $\mu_{2}<\mu_{1}$, i.e., when the object is observed from a rarer medium, it appears to be closer to the interface, i.e.

$\mathrm{d}_{\mathrm{AP}}<\mathrm{d}_{\mathrm{AC}}$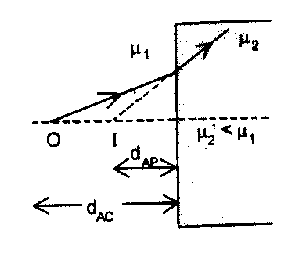

Note: The above formula is applicable only for normal view or paraxial ray assumption.

6. Relation between object and image Velocities:

(a.) If an object O moves toward the plane boundary of a denser medium then the image appears to be farther but moves faster to an observer in the denser medium. If $v_{0}=v$ then $v_{1}=\mu v$ Where $v_{0} \& v_{1}$ represents object and image velocities respectively.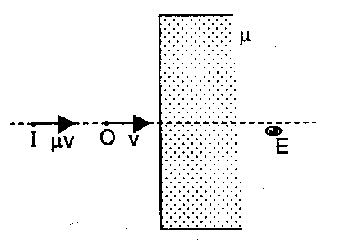

(b.) If an object O moves toward the plane boundary of a rarer medium then the image appears to be closer but moves slower to an observer in rarer medium. If $v_{0}=v$ then $v_{1}=v / \mu$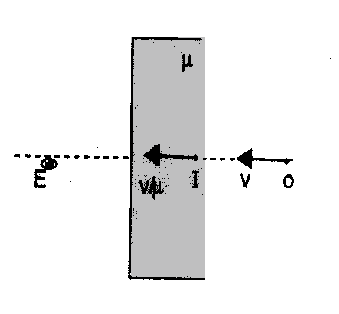

7. Deviation (d):

(a.) A light ray traveling from a denser to a rarer medium at an angle $\alpha<\theta_{\mathrm{C}}$ then deviation. 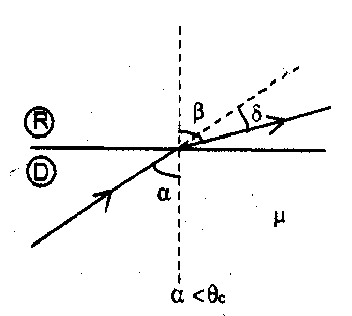$\delta=\beta-\alpha=\sin ^{-1}(\mu \sin \alpha)-\alpha$

and $\delta_{\max }=\frac{\pi}{2}-\theta_{\mathrm{c}}$

(b.)  If the light is incident at an angle $\alpha>\theta_{C}$, Then the angle of deviation is 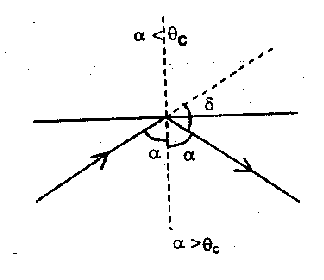$\delta=\pi-2 \alpha$ and $\delta_{\max }=\pi-2 \theta_{c}$

(c.) Graphically the relation between d & a can be shown as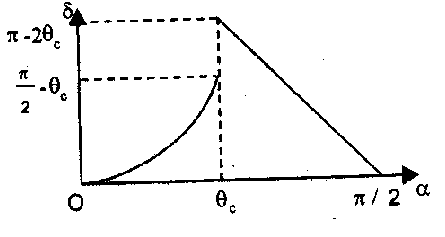

So, that's all from this article. I hope you get the idea about Snell's law of refraction. If you found this article informative then please share it with your friends. If you have any confusion related to this topic then feel free to ask in the comments section down below.

For a better understanding of this chapter, please check the detailed notes of Ray Optics. To watch Free Learning Videos on physics by Saransh Gupta sir Install the eSaral App.