Get Solid State important questions for Boards exams. Download or View the Important Question bank for Class 12 Chemistry. These important questions will play significant role in clearing concepts of Chemistry. This question bank is designed by NCERT keeping in mind and the questions are updated with respect to upcoming Board exams. You will get here all the important questions for class 12 chemistry chapter wise CBSE. Click Here for Detailed Chapter-wise Notes of Chemistry for Class 12th, JEE & NEET. You can access free study material for all three subject’s Physics, Chemistry and Mathematics. Click Here for Detailed Notes of any chapter.
eSaral provides you complete edge to prepare for Board and Competitive Exams like JEE, NEET, BITSAT, etc. We have transformed classroom in such a way that a student can study anytime anywhere. With the help of AI we have made the learning Personalized, adaptive and accessible for each and every one. Visit eSaral Website to download or view free study material for JEE & NEET. Also get to know about the strategies to Crack Exam in limited time period.
Q. What is the C.N of $\mathrm{Ca}^{2+}$ and $\mathrm{F}^{-}$ in $\mathrm{CaF}_{2}$ crystal lattice?
Ans. C.N of $C a^{2+}$ ion $=8,$ C.N. of $F^{-}$ ion $=4$
Q. How many particles are present in a face centred unit cell?
Ans. Four particles are present in each unit cell.
Q. How many atoms are there in a unit cell of a metal crystallising in fcc structure ?
Ans. Four
Q. A compound $\mathrm{AB}_{2}$ possesses the $\mathrm{CaF}_{2}$ type crystal structure. Write the coordination numbers of $\mathrm{A}^{2+}$ and $\mathrm{B}^{-}$ ions in its crystals.
Ans. Coordination no. of $\mathrm{A}=8,$ Coordination no. of $\mathrm{B}=4$
Q. What other element may be added to silicon to make electrons available for conduction of an electric current ?
Ans. Phosphorus.
Q. Define coordination number of a metal ion in an ionic crystal.
Ans. In an ionic crystal, coordination number of a metal ion (+ve ion) is the number of negative ions surrounding the metal ion, i.e., which are present as its nearest neighbours.
Q. At what temperature ferrimagnetic substance changes to paramagnetic ?
Ans. 850 K
Q. What is the co-ordination number of $\mathrm{Na}^{+}$ and $\mathrm{Cl}$ - ions in $\mathrm{NaCl}$ structure?
Ans. Six.
Q. Sodium chloride has a face centred cubic crystal. What is the co-ordination number of sodium in sodium chloride ?
Ans. Six
Q. What are the co-ordination numbers of each of the ions present in the cubic close packed structure of $\mathrm{Na}_{2} \mathrm{O}$ at ordinary temperature and pressure?
Ans. $N a=4, O=8$
Q. A metallic element crystallises into a lattice containing a sequence of layers of ABABAB $\ldots . .$ Any packing of spheres leaves out voids in the lattice. What percentage by volume of this lattice is empty space?
Ans. 26%
Q. AgI crystallises in cubic close packed ZnS structure. What fraction of tetrahedral sites are occupied by Ag" ions?
Ans. In the face-centred unit cell, there are eight tetrahedral voids. Of these, half are occupied by silver cations.
Q. The unit cell of a substance has cations $\mathrm{A}^{+}$ at the corners of the unit cell and the anions $\mathrm{B}^{-}$ in the centre. What is the simplest formula of the substance?
Ans. AB
Q. What is the maximum possible co-ordination number of an atom in an hcp crystal structure of an element?
Ans. 12
Q. In a crystal of zinc sulphide, zinc occupies tetrahedral voids. What is the co-ordination number of zinc ?
Ans. 4.
Q. Which out of $\mathrm{Cd} \mathrm{Cl}_{2}$ and $\mathrm{NaCl}$ will produce Schottky defect if added to $\mathrm{AgCl}$ crystal $?$
Ans. $\mathrm{CdCl}_{2}$ will produce Schottky defect.
Q. What type of stoichiometric defects are noticed in crystals ?
Ans. These are of two types i.e., Frenkel and Schottky defects.
Q. What type of semi-conductors is produced when silicon is doped with arsenic ?
Ans. It is of n-type because one electron of each silicon atom remains non-bonded.
Q. What is the effect of Frenkel defect on the electrical conductivity of crystalline solids ?
Ans. It increases because of the vacancies that are created.
Q. Why does Frenkel defect not change the density of AgCl crystals?
Ans. Due to Frenkel defect, as no ions are missing from the crystal as a whole, so there is no change in density.
Q. Mention one property which is caused due to the presence of Fcentre in a solid.
Ans. F-centre is reponsible for the colour and paramagnetic behaviour of the solid.
Q. What type of crystal defect is produced when sodium chloride is doped with MgCl_?
Ans. It is called impurity defect. A cation vacancy is produced. A substitutional solid solution is formed (because $2 \mathrm{Na}^{+}$ ion are replaced by one Mg $^{2+}$ ion in the lattice site).
Q. What causes the conduction of electricity by semiconductors ?
Ans. Electrons and holes produced by defects.
Q. A cubic solid is made up of two atoms A and B. Atoms A are present at the corners and B at the centre of the body. What is the formula of the unit cell ?
Ans. Contribution by the atoms A present at eight corners = 1 Contribution by the atom B present in the centre of the body = 1 Thus, the ratio of atoms of A : B = 1 : 1 Formula of unit cell = AB
Q. Define the term ‘amorphous’. Give a few examples of amorphous solids.
Ans. An amorphous solid is a substance whose constituent particles do not possess a regular orderly arrangement. Some examples of amorphous solids are glass, plastics, rubber, starch etc.
Q. Calculate the density of silver, which is known to crystallise in face-centred cubic form. distance nearest metal atoms is $287 \mathrm{pm}$ (Molar mass of $\left.\mathrm{Ag}=107.87 \mathrm{g} \mathrm{mol}^{-1} ; \mathrm{N}_{0}=6.022 \times 10^{23} \mathrm{mol}^{-1}\right)$
Ans. Density of unit cell $(\rho)=\frac{Z \times M}{N_{0} \times a^{3} \times 10^{-30}}$ According to available data, Distance between nearest metal atom $(2 r)=287 \mathrm{pm}$ Edge length for foc crytal $(a)=\sqrt{2} \times 2 r=405.87 \mathrm{pm}$ No. of atoms per unit cell $(z)=4$ Atomic mass of silver $(M)=107.87 \mathrm{gmol}^{-1}$ Avogadro's number $\left(N_{0}\right)=6.022 \times 10^{23} \mathrm{mol}^{-1}$ Density of silver $=\frac{4 \times 107.87 g m o l^{-1}}{(405.87)^{3} \times 6.022 \times 10^{23} \mathrm{mol}^{-1} \times 10^{-30} \mathrm{m}^{3}}$ $=10.77 \mathrm{g} \mathrm{cm}^{-3}$
Q. What is the distance between $N a^{+}$ and $C I^{-}$ ions in $N a C l$ crystal if its density is $2.165 \mathrm{g} \mathrm{cm}^{-3} ?$ crystallises in fec lattice?
Ans. Step I. Calculation of Edge Length of unit cell Let the edge length of unit cell $=a$ Volume of unit cell $=a^{3}$ Gram formula mass of $N a C l=23+35.5=585 g m o l^{1}$ No. of particles in foc type unit cell $(Z)=4$ Mass of unit cell $=\frac{Z \times \text { Gramformulamassof } N a C l}{\text { Avogadro's Number }\left(N_{0}\right)}$ $=\frac{4 \times\left(58.5 g \mathrm{mol}^{-1}\right)}{\left(6.022 \times 10^{23} \mathrm{mol}^{-1}\right)}=3.886 \times 10^{-22} \mathrm{g}$ Density of unit cell $(\rho)=2.165 g \mathrm{cm}^{-3}$ Now, Density of unit cell $=\frac{\left(3.886 \times 10^{-22} g\right)}{\text { Volume of unit cell }\left(a^{3}\right)}$ volume of unit cell $(a)=\frac{\left(3.886 \times 10^{-22} g\right)}{\left(2.165 g \mathrm{cm}^{-3}\right)}$ $=1.795 \times 10^{-22} \mathrm{cm}^{3}=179.5 \times 10^{-24} \mathrm{cm}^{3}$ Edge length $(\mathrm{a})=\left(179.5 \times 10^{-24} \mathrm{cm}^{3}\right)^{1 / 3}=5.64 \times 10^{-8} \mathrm{cm}$ \[ =564 \times 10^{-10} \mathrm{cm}=564 \mathrm{pm} \] Step II. Calculation of distance between $N a^{+}$ and $C l^{-}$ ions. Edge length of $N a^{+} C l^{-}$ unit cell $=2\left(r_{N a^{+}}+r_{C l}^{-}\right)$ $2\left(r_{N a^{+}}+r_{C I^{-}}\right)=564 \mathrm{pm}$ or $\left(r_{N a^{+}}+r_{C l^{-}}\right)=\frac{564}{2}=282 \mathrm{pm}$ $\therefore$ Distance in and ions $=282$ pm
Q. Calculate the value of Avogadro's number from the following data : Density of $\mathrm{NaCl}=2.165 \mathrm{g} \mathrm{cm}^{-3},$ Distance between $\mathrm{Na}^{+}$ and $\mathrm{Cl}^{-}$ ions in $\mathrm{NaCl}$ crystal $=281 \mathrm{pm}$
Ans. We know that $\rho=\frac{Z \times M}{a^{3} \times N_{0} \times 10^{30}}$ or $\quad N_{0}=\frac{Z \times M}{a^{3} \times \rho \times 10^{-30}}$ Edge length of $N a C l(a)=2\left(r_{N a^{+}}+r_{C l}\right)=2 . \times 281=562 \mathrm{pm}$ No. of atoms per unit cell $(Z)=4$ $(\because N a C l$ hasfcc structure) Density of $N a C l(\rho)=2.165 g \mathrm{cm}^{-3}$ Gram molecular mass of $N a C l(M)=23+35.5$ $=58.5 g \mathrm{mol}^{-1}$ $\therefore$ Avogadro's Number $\left(N_{0}\right)=\frac{4 \times\left(58.5 g m o l^{-1}\right)}{(562)^{3} \times\left(2.165 g \mathrm{cm}^{-3}\right) \times\left(10^{-30} \mathrm{cm}^{3}\right)}$ $=6.089 \times 10^{23} \mathrm{mol}^{-1}$
Q. How does the electrical conductivity of metallic conductors vary with temperature ?
Ans. Electrical conductivity decreases with increase in temperature because kernels start vibrating and create hinderance in the flow of electrons.
Q. What is the coordination number of (i) Sodium in sodium oxide $\left(\mathrm{Na}_{2} \mathrm{O}\right)$ (ii) Oxide ion in sodium oxide (Na,O)? (iii) Calcium in calcium fluoride $\left(\mathrm{CaF}_{2}\right) ?$ (iv) $\operatorname{zinc}$ in zinc blende (ZnS)?
Ans. (i) 4 (ii) 8 (iii) 8 (iv) 4 (v) 4.
Q. In CaF- $_{2}$ crystal $\mathrm{Ca}^{2+}$ ions are present in FCC arrangement. Calculate the number of $\mathrm{F}^{-}$ ions in the unit cell.
Ans. No. of $C a^{2+}$ ions per unit cell $=8 \times \frac{1}{8}+6 \times \frac{1}{2}=4 .$ Hence, no. of $F^{-}$ ions per unit cell $=2 \times 4=8$
Q. How many atoms can be assigned to its unit cell if an element forms (i) body-centred cubic cell (ii) a face-centred cubic cell.
Ans. (i) 2 (ii) 4.
Q. What are the types of lattice imperfections found in crystals ?
Ans. (a) Stoichiometric defects, viz., Schottky defect and Frenkel defect and (b) Non-stoichiometric defects, viz., metal excess, metal deficiency and impurity defects.
Q. What are non-soichiometric compounds ?
Ans. If the actual ratio of the cations and anions is not same as represented by the ideal chemical formula of the compound, it is called a non-stoichiometric compound.
Q. What is Frenkel defect ?
Ans. When some ions (usually cations) are missing from the lattice sites and they occupy the interstitial sites so that electrical neutrality as well as stoichiometry is maintained, it is called Frenkel defect
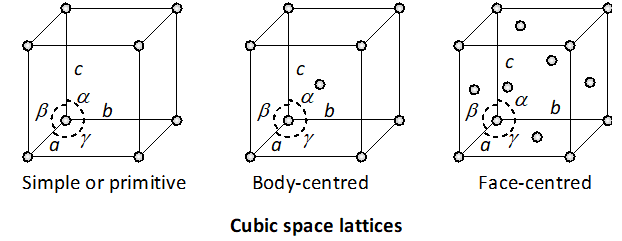
Q. Explain with the help of diagrams the structural differ-ences between three types of cubic crystals.
Ans. The crystals belonging to cubic system have three kinds of Bravais lattices. These are : (i) Simple cubic lattice
: There are points only at the corners of each unit. (ii) Face-centred cubic lattice
: There are points at the corners as well as at the centre of each of the six faces of the cube. (iii) Body-centred cubic lattice : There are points at the corners as well as in the body centre of each cube.
Q. What is the difference between ‘Schottky defects’ and ‘Frenkel detects’ ?
Ans. 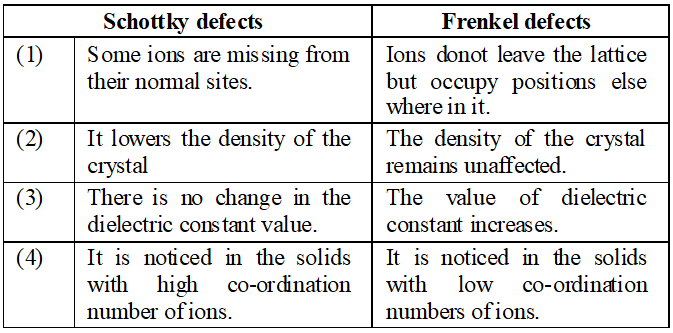
Q. Pure silicon is an insulator. Silicon doped with phosphorus is a semiconductor. Silicon doped with gallium is also a semiconductor. What is the difference between the two doped silicon semiconductors ?
Ans. When silicon is doped with phosphorus (a group 15 element) one electron of each phosphorus atom becomes free because it is not involved in any bonding with silicon atom. Thus, silicon containing phosphorus as the impurity is n-type semi-conductor. When silicon is doped with gallium (a group 13 element) only three valence electrons of silicon may be involved in the bonding with the three valence electrons of gallium. Since silicon atom has four valence electrons, this may result in creating vacancies or holes. These holes responsible for electrical conductivity and will result in p-type semi-conductors.
Q. Explain superconductivity.
Ans. There are certain solids called super conducting solids which do not offer any resistance to flow of electric current which means that they have zero resistivity. A few important examples are $B a_{7} K_{3} B i O_{3}, L a_{1.8} S r_{.2} C u O_{4}, Y B a_{2} C u_{3} O_{7}$ etc.
Q. Sodium crystallises in a body-centred cubic unit cell (bcc) with edge length 4.29 $\hat{\mathrm{A}}$. What is the radius of the sodium atom? What is the length of the body-diagonal of the unit cell?
Ans. For a body centred cubic unit cell (bcc)
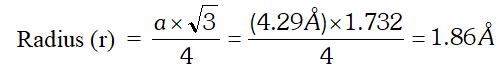
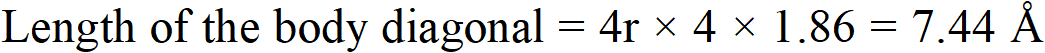
Q. Aluminium metal forms a cubic face centred close packed crystal structure. Its atomic radius is \[ 125 \times 10^{-12} \mathrm{m} \] (a) Calculate the length of the side of the unit cell. (b) How many unit cells are there in $1.0 \mathrm{m}^{3}$ of aluminium?
Ans. (a) For a face centred cubic lattice (fcc). Radius $(\mathrm{r})=\frac{a}{2 \sqrt{2}}$ $a=r \times 2 \sqrt{2}=125 \times 10^{-12} \times 2 \sqrt{2} m$ $=125 \times 2 \times 1.414 \times 10^{-12}=354 \times 10^{-12} \mathrm{m}$ (b) Volume of unit cell $(a)^{3}$ $=\left(354 \times 10^{-12}\right)^{3} m^{3}=4.436 \times 10^{-29} m^{3}$ No. of unit cells in $1.0 \mathrm{m}^{3}$ of $\mathrm{Al}$ $=\frac{\left(1.0 m^{3}\right)}{\left(4.436 \times 10^{-29} m^{3}\right)}=2.25 \times 10^{28}$
Q. The edge length of $\mathrm{NaCl}$ unit cell is 564 pm. What is the density of $\mathrm{NaCl}$ in $\mathrm{g} / \mathrm{cm}^{3} ?$
Ans. Density of unit cell $(\rho)=\frac{Z \times M}{a^{3} \times N_{0} \times 10^{-30}}$ According to available data, Edge length $(a)=564$ pm Molar mass of $N a C l(M)=23+35.5=58.5 \mathrm{g} \mathrm{mol}^{-1}$ No. of atoms per unit cell" $(Z)=4$ Avogadro's number $\left(N_{0}\right)=6.022 \times 10^{23} \mathrm{mol}^{-1}$ Density of unit cell $=\frac{4 \times\left(58.5 g m o l^{-1}\right)}{(564)^{3} \times\left(6.022 \times 10^{23} \mathrm{mol}^{-1}\right) \times\left(10^{-30} \mathrm{cm}^{3}\right)}$ $=2.16 g \mathrm{cm}^{-3}$
Q. Cesium chloride crystallises as a body centred cubic lattice and has a density of $4.0 \mathrm{gcm}^{-3} .$ Calculate the edge length of unit cell of cesium chloride crystal. (Moalr mass of $\left.\mathrm{CsCl}=168.5 \mathrm{g} \mathrm{mol}^{-1} ; \mathrm{N}_{\mathrm{A}}=6.02 \times 1023 \mathrm{mol}^{-1}\right)$
Ans. Density of unit cell $(\rho)=\frac{Z \times M}{N_{0} \times a^{3} \times 10^{-30}}$ or $\quad a^{3}=\frac{Z \times M}{\rho \times N_{0} \times 10^{-30}}$ According to available data, No. of atoms in the b.c.c. unit cell $(Z)=2$ Density of unit cell $(\rho)=4.0 \mathrm{g} \mathrm{cm}^{-3}$ Molar mass of $\operatorname{CsCl}(M)=168.5 \mathrm{g} \mathrm{mol}^{-1}$ Avogadro's no. $\left(N_{0}\right)=6.02 \times 10^{23} \mathrm{mol}^{-1}$ By substituting the values, $a^{3}=\frac{2 \times\left(168.5 g m o l^{-1}\right)}{\left(4.0 g c m^{-3}\right) \times\left(6.02 \times 10^{23} \mathrm{mol}^{-1}\right) \times 10^{-30}}$ $=1.399 \times 10^{8}(p m)^{3}$ Edge length $(a)=\left[1.399 \times 10^{8}(p m)^{3}\right]^{1 / 3}$ (.: Value of a is in pm) $=1.12 \times 10^{2} \mathrm{pm}$
Q. How can you determine the atomic mass of an unknown metal if you know its density and the dimension of its unit cell ? Explain
Ans. (a) The number of nearest neighbours in a packing is called coordination number. For example, in hexagonal close packing (HCP) in three dimensions each atom (or constituent particle) is touching 12 other atoms. So its coordination number is 12 . (b) $\quad$ (i) In cubic close-packed structures each atom is in direct contact with 12 other atoms. Hence, its coordination number is 12 (ii) In body centred cubic structure coordination number is $8 .$
Q. ‘Stability of a crystal is reflected in the magnitude of its melting point.’ Comment. Collect melting point of solid water, ethyl alcohol, diethyl ether, and methane from a data book. What can you say about the intermolecular forces between these molecules.
Ans. A solid having stronger interparticle forces has higher melting point and is more stable. Thus, we can get an idea about stability of a crystal from its melting point. More stable crystals have higher melting points than less stable crystal. Thus, it is correct to say that stability of a crystal is reflected in magnitude of its melting point. Methane < Diethyl ether < Ethyl alcohol < Water Water having highest melting point has the strongest interparticle forces whereas methane having lowest melting point has the weakest intermolecular forces. The intermolecular forces in these molecules are in the order : Methane < Diethyl ether < Ethyl alcohol < Water
Q. How will you distinguish between the following pairs of terms (a) Hexagonal close packing and cubic close packing (b) Crystal lattice and unit cell (c) Tetrahedral void and octahedral void.
Ans. (a) In hexagonal close packing every third layer is similar to the first layer. Thus there is ABAB ...........arrangement. In cubic close packing every fourth layer is similar to first thus, there is ABC ABC ..... arrangement. (b) A crystal lattice may be defined as a regular three dimensional arrangement of identical points in space. While a unit cell may be defined as a three dimensional group of lattice points that generates the whole lattice by translation or stacking. (c) The vacant space between four touching sphere is called tetrahedral void. Centres of these spheres occupy corners of regular tetrahedron. The interstitial void formed by combination of two triangular voids of the first and second layer is called octahedral void because this is enclosed between six spheres, centres of which occupy corners of a regular octahedron.
Q. What is a semiconductor ? Describe the two main types of semiconductors and contrast their conduction mechanisms.
Ans. Semi-conductors. These are the solids whose conductivity lies in-between those of conductors and insulators. It normally ranges between $10^{-6}$ to $10^{4}$ ohm $^{-1} \mathrm{cm}^{-1} .$ They, infact allow only a portion of applied electric current to pass through them.
Conduction of electricity in semi-conductors The electric conductivity of semi conductors is explained with the help of band theory. As we know, there is only a small energy gap between valence band (filled band) and conduction band (empty band) in semi-conductors. Therefore, some electrons can jump from valence band to vacant band and electric conductance is thus, possible. It can further increases with the rise in temperature since more electrons can jump to the conduction band.
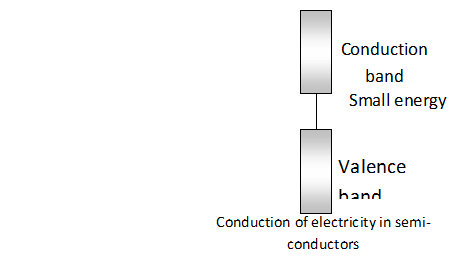 Intrinsic semi-conductors.
Intrinsic semi-conductors. The extrinsic semi-conductors are formed when impurities of certain elements are added to the insulators.
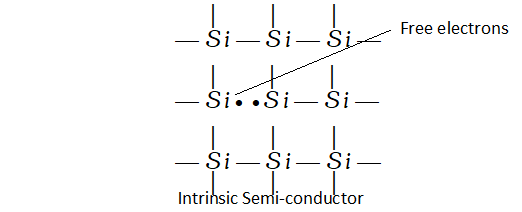
This process known as doping makes available electrons or holes for conductivity and thus, leads to two types of semi-conduction. These are called n-type semi-conductors and p-type semi-conductors.
n-type semi-conductors. n-type semiconductors are formed when impurity atoms containing more valence electrons than the atoms of the parent in insulator are introduced in it. These are called
electron rich impurities. For example, when traces of phosphorus (a group 15 element) is added to pure silicon (a group 14 element) on electron of each phosphorus atom (has five valence electrons) becomes free because it is not involved in any bonding with silicon atom (has four valence electrons). The unbonded electrons are free to carry the electric current. Thus, silicon containing phosphorus as the impurity is
n-type semi-conductor. 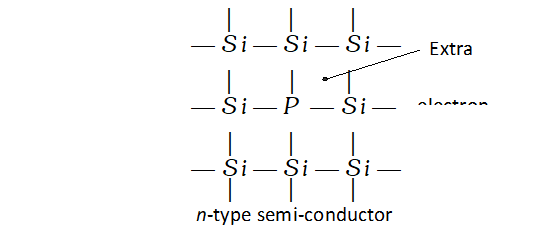
(ii)
p-type semi-conductors. These are formed when impurity atoms containing lesser number of valence electrons than the atoms of the parent insulator element added to it. These are called electron deficient impurities. For example, when traces of boron. (a group 13 element) are added to pure silicon (a group 14 element) only three valence electrons of silicon may be involved in the bonding with the three valence electrons of boron. Since silicon atom has four valence electrons, this may result in creating vacancies or holes. These holes are responsible for electrical conductivity and will result in p-type semi-conductors.
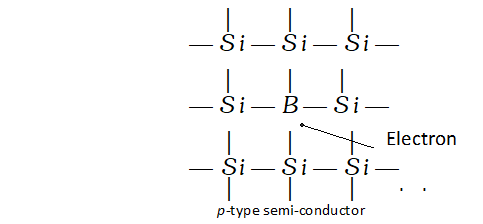
Q. Classify each of the following as being either a p-type or an n-type semiconductor : (i) Ge doped with In (ii) B doped with Si
Ans. (i) Ge is an element of group- 14 and has configuration $4 s^{2} 4 p^{2}$ It has been doped with In, a $13^{\text {th }}$ group element having $5 s^{2} 5 p^{1}$ configuration. All three valence electrons of In get bonded with three out of four electrons of Ge. Thus, the fourth bond of Ge contains only one electron and hence is an electron deficient bond or a hole. Conductivity is due to these holes or electron deficient bonds. Therefore, it is a p-type semiconductor. (ii) Boron, $\mathrm{B}$ is an element of group- 13 and has $2 s^{2} 2 p^{1}$ configuration. It is doped with $S i,$ an element of group- 14 having $3 s^{2} 3 p^{2}$ configuration. All three electrons of boron get bonded with 3 out of 4 electrons of Si and $4^{\text {th }}$ electron of impurity atom (i.e., Si) is responsible for conductivity. Thus it is a n-type semiconductor.
Q. An element crystallises in a bcc structure. The edge length of its unit cell is 288 pm. If the density of the crystal is $7.3 \mathrm{g} \mathrm{cm}^{-3}$, what is the atomic mass of the element?
Ans. We know that $\rho=\frac{Z \times M}{a^{3} \times N_{0} \times 10^{-30}}$ or $M=\frac{\rho \times a^{3} \times N_{0} \times 10^{-30}}{Z}$ According to available data, Edge length $(a)=288$ pm No. of atoms per unit cell $(Z)=2$ $(\because \text { bcc structure })$ Density of the element $=7.3 \mathrm{g} \mathrm{cm}^{-3}$ Avogadro's No. $\left(N_{0}\right)=6.022 \times 10^{23} \mathrm{mol}^{-1}$
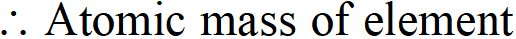
$=52.51 g \mathrm{mol}^{-1}$
Q. The element chromium crystallises in a body centred cubic lattice whose density is $7.20 \mathrm{g} / \mathrm{cm}^{3} .$ The length of the edge of the unit cell is $288.4 \mathrm{pm} .$ Calculate Avogadro's number (Atomic mass of $\mathrm{Cr}=52)$
Ans. We know that $\rho=\frac{Z \times M}{a^{3} \times N_{0} \times 10^{-30}}$ Or $N_{0}=\frac{Z \times M}{a^{3} \times \rho \times 10^{-30}}$ Edge length of the unit cell $(\mathrm{a})=288.4 \mathrm{pm}$ No. of atoms per unit cell $(Z)=2$ Density of the unit cell $(\rho)=7.2 \mathrm{g} / \mathrm{cm}^{3}$ Atomic mass of the element $(\mathrm{M})=52 \mathrm{g} \mathrm{mol}^{-1}$ $N_{0}=\frac{2 \times\left(52 g m o l^{-1}\right)}{(288.4)^{3} \times\left(7.2 g \mathrm{cm}^{-3}\right) \times\left(10^{-30} \mathrm{cm}^{3}\right)}$ $=6.04 \times 10^{23} \mathrm{mol}^{-1}$
Q. The density of chromium is $7.2 \mathrm{g} \mathrm{cm}^{-3} .$ If the unit cell is a cubic with edge length of 289 pm, determine the type of the unit cell. (Atomic mass of $\mathrm{Cr}=52$ amu)
Ans. We know that $\rho=\frac{Z \times M}{a^{3} \times N_{0} \times 10^{-30}}$ or $\quad Z=\frac{\rho \times a^{3} \times N_{0} \times 10^{-30}}{M}$ Gram atomic mass of $C r(M)=52.0 \mathrm{gmol}^{-1}$ Edge length of unit cell $(\mathrm{a})=289 \mathrm{pm}$ Density of unit cell $(\rho)=7.2 \mathrm{g} \mathrm{cm}^{-3}$ Avogadro's number $\left(N_{0}\right)=6.022 \times 10^{23} \mathrm{mol}^{-1}$ $\therefore Z=\frac{\left(7.2 g \mathrm{cm}^{-3}\right) \times\left(289^{3} \times\left(6.022 \times 10^{23} \mathrm{mol}^{1}\right) \times\left(10^{-30} \mathrm{cm}^{3}\right)\right.}{\left(520 \mathrm{gmol}^{1}\right)}=2$ since the unit cell has 2 atoms, it is body centre in nature.
Q. Calculate the efficiency of packing in case of a metal crystal for (a) Simple cubic (b) Body centred cubic (c) Face centred cubic
Ans. (a)
Packing Efficiency of Simple Cubic Structure In a simple cubic unit cell there is only one atom per unit cell. Let a be the edge length of the unit cell and r be the radius of sphere. Volume of the sphere $=\frac{4}{3} \pi r^{3}$ As the spheres at the corners are touching each other, the edge length a is equal to $2 \mathrm{r}$. Volume of the cube $=a^{3}=(2 r)^{3}=8 r^{3}$ $\%$ of the space occupied by spheres $=\frac{\text { Volume of sphere }}{\text { Volume of cube }} \times 100=\frac{\frac{4}{3} \pi r^{3}}{8 r^{3}} \times 100$
Thus, packing efficiency of simple cubic lattice is 52.4% (b)
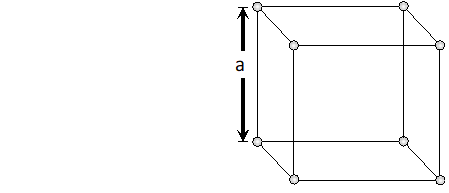
Packing Efficiency of Body Centred Cubic (BCC) Structure We know that in a body centred cubic unit cell there are two spheres per unit cell. Let a be the side of the unit cell and r be the radius of sphere. volume of sphere $=\frac{4}{3} \pi r^{3}$ Volume occupied by two spheres $=2 \times \frac{4}{3} \pi r^{3}=\frac{8}{3} \pi r^{3}$
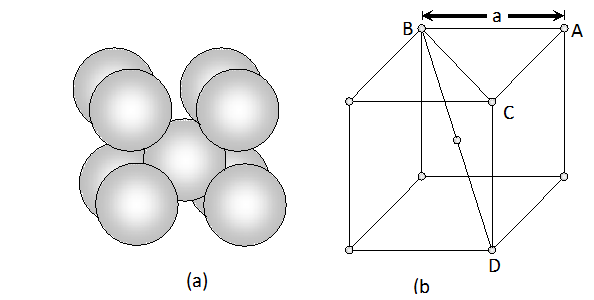
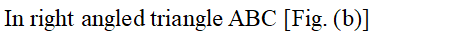
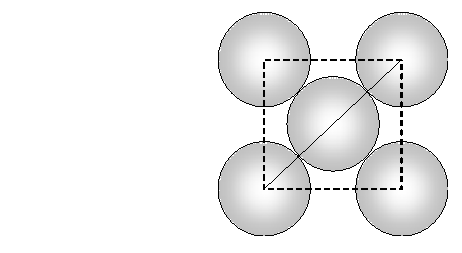
Face diagonal $A C=\sqrt{A B^{2}+B C^{2}}=\sqrt{2 a^{2}}$ In right angled triangle ACD Body diagonal $A D=\sqrt{A C^{2}+C D^{2}}=\sqrt{2 a^{2}+a^{2}}=\sqrt{3} a$ In a body centred cubic unit cell, the spheres at the corners are not touching each other but are in contact with the sphere at the centre. As a result the body diagonal AD is equal to the four times the radius of the sphere. $\therefore A D=\sqrt{3} a=4 r$ $a=\frac{4}{\sqrt{3}} r$ Volume of unit cell $=a^{3}=\left(\frac{4}{\sqrt{3}} r\right)^{3}=\frac{64}{3 \sqrt{3}} r^{3}$ Percentage of space occupied by spheres $=\frac{\text { Volume of spheres }}{\text { Volume of cube }} \times 100$ $=\frac{\frac{8}{3} \pi r^{3}}{\frac{64}{3 \sqrt{3}} r^{3}} \times 100=\frac{8}{3} \times \frac{22}{7} \times \frac{3 \sqrt{3}}{64} \times 100=68 \%$ Thus, packing efficiency of a bcc arrangement is $68 \% .$ (c) Face centred cubic In a cubic close packing, the unit cell is face centred cube. In a face centred cubic unit cell there are 4 spheres per unit cell. Let r be the radius of sphere and a be the edge length of the cube. Volume of sphere $=\frac{4}{3} \pi r^{3}$ Volume of four spheres $=4 \times \frac{4}{3} \pi r^{3}=\frac{16}{3} \pi r^{3}$ 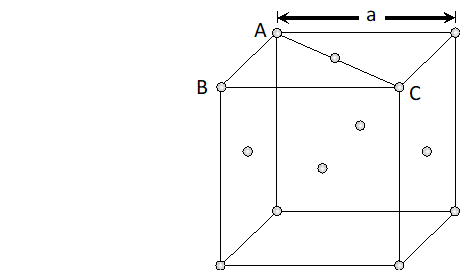 In a face centred cubic unit cell, the spheres at corners are in contact with sphere at the face centre but are not touching each other. Therefore, face diagonal $\mathrm{AC}$ is equal to four times the radius of sphere. $A C=4 r$ But in right angled triangle ABC (figure) $A C=\sqrt{A B^{2}+B C^{2}}=\sqrt{a^{2}+a^{2}}=\sqrt{2} a$ $\therefore \sqrt{2} a=4 r$ $a=\frac{4 r}{\sqrt{2}}$ Volume of the unit cell $=a^{3}=\left(\frac{4 r}{\sqrt{3}}\right)^{3}=\frac{64}{2 \sqrt{2}} r^{3}$ Percentage of space occupied by spheres $=\frac{\text { Volume of spheres }}{\text { Volume of cube }} \times 100=\frac{\frac{16}{3} \pi^{3}}{\frac{64}{2 \sqrt{2}} r^{3}} \times 100$ $=\frac{16}{3} \times \frac{22}{7} \times \frac{2 \sqrt{2}}{64} \times 100=74 \%$ Thus, packing efficiency of ccp arrangement is 74%. Similarly, packing efficiency of hcp is also 74%.
In a face centred cubic unit cell, the spheres at corners are in contact with sphere at the face centre but are not touching each other. Therefore, face diagonal $\mathrm{AC}$ is equal to four times the radius of sphere. $A C=4 r$ But in right angled triangle ABC (figure) $A C=\sqrt{A B^{2}+B C^{2}}=\sqrt{a^{2}+a^{2}}=\sqrt{2} a$ $\therefore \sqrt{2} a=4 r$ $a=\frac{4 r}{\sqrt{2}}$ Volume of the unit cell $=a^{3}=\left(\frac{4 r}{\sqrt{3}}\right)^{3}=\frac{64}{2 \sqrt{2}} r^{3}$ Percentage of space occupied by spheres $=\frac{\text { Volume of spheres }}{\text { Volume of cube }} \times 100=\frac{\frac{16}{3} \pi^{3}}{\frac{64}{2 \sqrt{2}} r^{3}} \times 100$ $=\frac{16}{3} \times \frac{22}{7} \times \frac{2 \sqrt{2}}{64} \times 100=74 \%$ Thus, packing efficiency of ccp arrangement is 74%. Similarly, packing efficiency of hcp is also 74%.
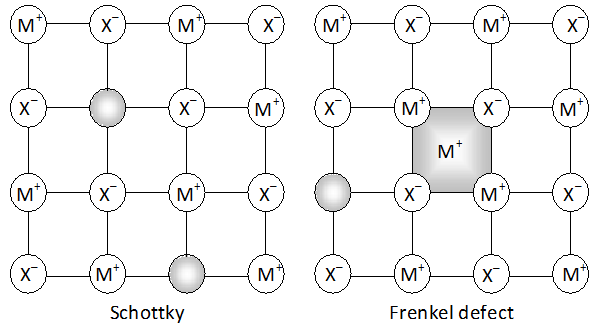
Q. Explain the following terms with suitable examples : (i) Schottky defect (ii) Frenkel defect (iii) Interstitials (iv) F-centres
Ans. (i) Schottky Defects. This type of defect is created when one positive ion and one negative ion are missing from their respective positions leaving behind a pair of holes (figure.). Schottky defect are more common in ionic compounds with high co-ordination number, and where the sizes of positive and negative ions are almost equal. For example, $N a C l, K C l, C s C l, A g B r$ and $K B r .$ $\mathrm{NaCl}$ has one defect in $10^{15}$ lattice sites at room temperature. The number of defects increases with increases in temperature. The number of defects increases to one in $10^{6}$ sites at $775 \mathrm{K}$ and one in $10^{4}$ sites at $1075 \mathrm{K} .$ The presence of large number of Schottky defects in crystal results in significant decrease in its density. This defect is also known as vacancy defect. (ii) Frenkel Defect. This type of defect is created when an ion leaves its correct lattice site and occupies an interstitial site (fig. Frenkel defects are common in ionic compound which have low co-ordination number and in which there is large difference in size between positive and negative ions. For example, $Z n S, A g C l, A g B r$ and $A g I$
(iii)
Interstitial Defects. This type of defect is caused due to the presence of ions in the normally vacant interstitial sites in the crystal. The ions occupying the interstitial sites are called interstitials. The formation of interstitial defects in determined by the size of the interstitial ion. (iv) The "holes' occupied by electrons are called F-centres (or colour centres) and are responsible for the colour of the compound and many other interesting properties. For example, the excess sodium in $\mathrm{NaCl}$ makes the crystal appear yellow, excess potassium in $K C l$ makes it violet and excess lithium in LiClmakes it pink. Greater the number of F-centres, greater is the intensity of colour. Solids containing F-centres are paramagnetic because the electrons occupying the "holes' are unpaired.
Q. Aluminium crystallizes in a cubic close packed structure. Its metallic radius is $125 \mathrm{pm} .$ (a) What is the length of the side of the unit cell? (b) How many unit cells are there in $1.00 \mathrm{cm}^{3}$ of aluminium?
Ans. (a) In cubic close packed structure, face diagonal of the unit cell is equal to four times the atomic radius Face diagonal $=4 \times r=4 \times 125 \mathrm{pm}=500 \mathrm{pm}$ But face diagonal $=\sqrt{2} \times$ edge length $\therefore$ Edge length $=\frac{\text { Face diagonal }}{\sqrt{2}}=\frac{500}{\sqrt{2}}=354 \mathrm{pm}$
(b) Volume of one unit cell $=\mathrm{a}^{3}$ $=\left(3.54 \times 10^{-8} \mathrm{cm}\right)^{3}$ No. of unit cells $1.00 \mathrm{cm}^{3}$ $=\frac{1.00}{\left(3.54 \times 10^{-8}\right)^{3}}$ $=2.26 \times 10^{22}$


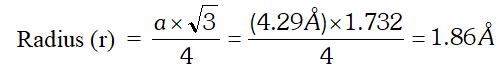
 Intrinsic semi-conductors. The extrinsic semi-conductors are formed when impurities of certain elements are added to the insulators.
Intrinsic semi-conductors. The extrinsic semi-conductors are formed when impurities of certain elements are added to the insulators.  This process known as doping makes available electrons or holes for conductivity and thus, leads to two types of semi-conduction. These are called n-type semi-conductors and p-type semi-conductors. n-type semi-conductors. n-type semiconductors are formed when impurity atoms containing more valence electrons than the atoms of the parent in insulator are introduced in it. These are called electron rich impurities. For example, when traces of phosphorus (a group 15 element) is added to pure silicon (a group 14 element) on electron of each phosphorus atom (has five valence electrons) becomes free because it is not involved in any bonding with silicon atom (has four valence electrons). The unbonded electrons are free to carry the electric current. Thus, silicon containing phosphorus as the impurity is n-type semi-conductor.
This process known as doping makes available electrons or holes for conductivity and thus, leads to two types of semi-conduction. These are called n-type semi-conductors and p-type semi-conductors. n-type semi-conductors. n-type semiconductors are formed when impurity atoms containing more valence electrons than the atoms of the parent in insulator are introduced in it. These are called electron rich impurities. For example, when traces of phosphorus (a group 15 element) is added to pure silicon (a group 14 element) on electron of each phosphorus atom (has five valence electrons) becomes free because it is not involved in any bonding with silicon atom (has four valence electrons). The unbonded electrons are free to carry the electric current. Thus, silicon containing phosphorus as the impurity is n-type semi-conductor.  (ii) p-type semi-conductors. These are formed when impurity atoms containing lesser number of valence electrons than the atoms of the parent insulator element added to it. These are called electron deficient impurities. For example, when traces of boron. (a group 13 element) are added to pure silicon (a group 14 element) only three valence electrons of silicon may be involved in the bonding with the three valence electrons of boron. Since silicon atom has four valence electrons, this may result in creating vacancies or holes. These holes are responsible for electrical conductivity and will result in p-type semi-conductors.
(ii) p-type semi-conductors. These are formed when impurity atoms containing lesser number of valence electrons than the atoms of the parent insulator element added to it. These are called electron deficient impurities. For example, when traces of boron. (a group 13 element) are added to pure silicon (a group 14 element) only three valence electrons of silicon may be involved in the bonding with the three valence electrons of boron. Since silicon atom has four valence electrons, this may result in creating vacancies or holes. These holes are responsible for electrical conductivity and will result in p-type semi-conductors. 
 Thus, packing efficiency of simple cubic lattice is 52.4% (b) Packing Efficiency of Body Centred Cubic (BCC) Structure We know that in a body centred cubic unit cell there are two spheres per unit cell. Let a be the side of the unit cell and r be the radius of sphere. volume of sphere $=\frac{4}{3} \pi r^{3}$ Volume occupied by two spheres $=2 \times \frac{4}{3} \pi r^{3}=\frac{8}{3} \pi r^{3}$
Thus, packing efficiency of simple cubic lattice is 52.4% (b) Packing Efficiency of Body Centred Cubic (BCC) Structure We know that in a body centred cubic unit cell there are two spheres per unit cell. Let a be the side of the unit cell and r be the radius of sphere. volume of sphere $=\frac{4}{3} \pi r^{3}$ Volume occupied by two spheres $=2 \times \frac{4}{3} \pi r^{3}=\frac{8}{3} \pi r^{3}$ 
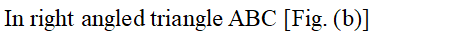
 In a face centred cubic unit cell, the spheres at corners are in contact with sphere at the face centre but are not touching each other. Therefore, face diagonal $\mathrm{AC}$ is equal to four times the radius of sphere. $A C=4 r$ But in right angled triangle ABC (figure) $A C=\sqrt{A B^{2}+B C^{2}}=\sqrt{a^{2}+a^{2}}=\sqrt{2} a$ $\therefore \sqrt{2} a=4 r$ $a=\frac{4 r}{\sqrt{2}}$ Volume of the unit cell $=a^{3}=\left(\frac{4 r}{\sqrt{3}}\right)^{3}=\frac{64}{2 \sqrt{2}} r^{3}$ Percentage of space occupied by spheres $=\frac{\text { Volume of spheres }}{\text { Volume of cube }} \times 100=\frac{\frac{16}{3} \pi^{3}}{\frac{64}{2 \sqrt{2}} r^{3}} \times 100$ $=\frac{16}{3} \times \frac{22}{7} \times \frac{2 \sqrt{2}}{64} \times 100=74 \%$ Thus, packing efficiency of ccp arrangement is 74%. Similarly, packing efficiency of hcp is also 74%.
In a face centred cubic unit cell, the spheres at corners are in contact with sphere at the face centre but are not touching each other. Therefore, face diagonal $\mathrm{AC}$ is equal to four times the radius of sphere. $A C=4 r$ But in right angled triangle ABC (figure) $A C=\sqrt{A B^{2}+B C^{2}}=\sqrt{a^{2}+a^{2}}=\sqrt{2} a$ $\therefore \sqrt{2} a=4 r$ $a=\frac{4 r}{\sqrt{2}}$ Volume of the unit cell $=a^{3}=\left(\frac{4 r}{\sqrt{3}}\right)^{3}=\frac{64}{2 \sqrt{2}} r^{3}$ Percentage of space occupied by spheres $=\frac{\text { Volume of spheres }}{\text { Volume of cube }} \times 100=\frac{\frac{16}{3} \pi^{3}}{\frac{64}{2 \sqrt{2}} r^{3}} \times 100$ $=\frac{16}{3} \times \frac{22}{7} \times \frac{2 \sqrt{2}}{64} \times 100=74 \%$ Thus, packing efficiency of ccp arrangement is 74%. Similarly, packing efficiency of hcp is also 74%.  (iii) Interstitial Defects. This type of defect is caused due to the presence of ions in the normally vacant interstitial sites in the crystal. The ions occupying the interstitial sites are called interstitials. The formation of interstitial defects in determined by the size of the interstitial ion. (iv) The "holes' occupied by electrons are called F-centres (or colour centres) and are responsible for the colour of the compound and many other interesting properties. For example, the excess sodium in $\mathrm{NaCl}$ makes the crystal appear yellow, excess potassium in $K C l$ makes it violet and excess lithium in LiClmakes it pink. Greater the number of F-centres, greater is the intensity of colour. Solids containing F-centres are paramagnetic because the electrons occupying the "holes' are unpaired.
(iii) Interstitial Defects. This type of defect is caused due to the presence of ions in the normally vacant interstitial sites in the crystal. The ions occupying the interstitial sites are called interstitials. The formation of interstitial defects in determined by the size of the interstitial ion. (iv) The "holes' occupied by electrons are called F-centres (or colour centres) and are responsible for the colour of the compound and many other interesting properties. For example, the excess sodium in $\mathrm{NaCl}$ makes the crystal appear yellow, excess potassium in $K C l$ makes it violet and excess lithium in LiClmakes it pink. Greater the number of F-centres, greater is the intensity of colour. Solids containing F-centres are paramagnetic because the electrons occupying the "holes' are unpaired. 
