Get Solution & Colligative Properties important questions for Boards exams. Download or View the Important Question bank for Class 12 Chemistry. These important questions will play significant role in clearing concepts of Chemistry. This question bank is designed by NCERT keeping in mind and the questions are updated with respect to upcoming Board exams. You will get here all the important questions for class 12 chemistry chapter wise CBSE. Click Here for Detailed Chapter-wise Notes of Chemistry for Class 12th, JEE & NEET. You can access free study material for all three subject’s Physics, Chemistry and Mathematics. Click Here for Detailed Notes of any chapter. eSaral provides you complete edge to prepare for Board and Competitive Exams like JEE, NEET, BITSAT, etc. We have transformed classroom in such a way that a student can study anytime anywhere. With the help of AI we have made the learning Personalized, adaptive and accessible for each and every one.
Visit eSaral Website to download or view free study material for JEE & NEET. Also get to know about the strategies to Crack Exam in limited time period.
Q. Why does molality of a solution remain unchanged with the rise in temperature ? [AI 2004 C]
Ans. Mass of solvent does not change with temperature.
Q. What is van’t Hoff equation for dilute solution ?
Ans. $\pi V=n R T$ where $n$ is the no. of moles of solute present in $V$ litres of solution, $\pi$ is osmotic pressure, $T$ is temperature and $R$ is gas constant or solution constant.
Q. Mention a large scale use of the phenomenon called ‘reverse osmosis’.
[Delhi 2004; CBSE 2004]
Ans. It is used for desalination of sea water.
Q. What do you understand by ‘colligative properties’? [Delhi 1999]
Ans. Colligative properties are those properties which depends upon number of particles of solute and not on natures of solute.
Q. Why is the cooking temperature in pressure cooker higher than in open pan ? [Delhi 2002 C]
Ans. In pressure cooker, high pressure is exerted by steam due to which boiling point becomes higher than in open pan.
Q. What is it that elevation in boiling point of water is not same in following solutions? 0.1 molar $N a C l$ solution and 0.1 molar sugar solution.
Ans. $0.1 M N a C /$ has higher elevation in boiling point because it contains more number of particles than $0.1 M$ solution of glucose. $N a C l \rightarrow N a^{+}+C l^{-}$
Q. What is de-icing agent ? How does it work ?
Ans. Common salt is called de-icing agent because it lowers the freezing point of water to such an extent that it does not freeze to form ice. Hence, it is used to clear snow from roads.
Q. Why is the vapour pressure of a solution of glucose in water lower than that of water ? [A.I.S.B. 2006]
Ans. At a number of sites, non-volatile glucose molecules will occupy the surface instead of water molecules. Hence, effective surface area for evaporation decreases and so the vapour pressure is lower.
Q. Give one example each of solid in gas and liquid in gas solutions. [H.P.S.B. 1998]
Ans. Iodine vapour in air, aerated drinks.
Q. What happens when blood cells are placed in pure water ? [Delhi 2003, 04; D.S.B. 2004 C]
Ans. Due to osmosis, water molecules move into blood cells through the cells walls. As a result, blood cells swell and may even burst.
Q. Write expression for the Raoult’s law for non-volatile solutes.
Ans. $\left(p^{\circ}-p_{s}\right) / p^{\circ}=n_{2} /\left(n_{1}+n_{2}\right)$ where $p^{\circ}=V . P .$ of pure solvent $p_{s}=V . P .$ of solution, $n_{2}=$ no. of moles of solute and $n_{1}=$ no. of moles of solvent.
Q. What is the difference between lowering of vapour pressure and relative lowering of vapour pressure ?
Ans. Lowering of V.P. $=p^{\circ}-p_{s} .$ Relative lowering of V.P. $=\left(p^{\circ}-p_{s}\right) / p^{\circ}$
Q. State any two characteristic of ideal solution. [Delhi 1999; Foreign 1999]
Ans. Ideal solutions (i) Follow Raoult’s law (ii) They can be separated by fractional distillation
Q. On mixing equal volumes of water and ethanol, what type of deviation would you expect from Raoult’s law ? [Delhi 1999 C]
Ans. It is because of $H$ -bonding between acetone and $C H C l_{3}$, the force of attraction increases, therefore energy is released.
Q. Why are ethers not miscible in water ?
Ans. Because they can not form H-bonds with water.
Q. Why is benzene insoluble in water but soluble in toluene? [AI 1999 C]
Ans. Benzene is insoluble in water because benzene is non polar where as water is polar. Toluene is non polar solvent therefore, Benzene is soluble in toluene.
Q. Give an example of a compound in which hydrogen bonding results in the formation of a dimer.
Ans. Acetic acid forms dimer due to H-bonding.
Q. Why is freezing point depression 0.1 M sodium chloride solution nearly twice that of 0.1 M glucose solution ? [A.I.S.B. 2006]
Ans. $\mathrm{NaCl},$ being an electrolytes, dissociates almost completely to give $N a^{+}$ and $\quad C I^{-}$ ions whereas glucose, being nonelectrolyte, does not dissociate. Hence, the number of particles in 0.1 MNaCl solution is nearly double than in $0.1 M$ glucose solution. Freezing point depression, being a colligative properly, is therefore, nearly twice for solution than for glucose solution of same molarity.
Q. State the formula relating pressure of a gas with its mole fraction in a liquid solution in contact with it. [DSB2005]
Ans. According to Henry’s law. Partial pressure of gas above the solution $=k_{H} \times$ mole fraction of the gas in the solution or $\quad p_{A}=k_{H} \times x_{A^{\prime}}$ where $k_{H}=$ Henry's constant.
Q. When fruits and vegetables are dried and placed in water, they slowly swell and return to original form. Why ? Does an increase in temperature accelerate the process ? Explain.
Ans. When fruits and vegetables that have dried and are placed in water osmosis takes place, i.e., water molecules pass through semipermiable membranes present in cell walls, therefore, they swell. If temperature is increased, osmosis will be faster.
Q. Why does the use of pressure cooker reduce cooking time?
Ans. At higher pressure over the liquid (due to weight of the pressure cooker lid), the liquid boils at higher temperature. Therefore, cooking occurs faster.
Q. Sodium chloride solution freezes at lower temperature than water but boils at higher temperature than water. Explain.
Ans. Freezing point of a liquid depresses on the addition of a non-volatile solute and therefore, a solution of sodium chloride freezes at lower temperature than freezing point of water. On he other hand, there is elevation in boiling point on the addition of a non-volatile solute and consequently boiling point of sodium chloride solution is more than that of water.
Q. Addition of $\mathrm{HgI}_{2}$ to aqueous solution of $K I$ shows an increase in vapour pressure. Why?
Ans. HgI$_{2}$ forms a complex with $K I$ and therefore, the number of particles in solution increases. $H g I_{2}+2 K I \rightarrow K_{2}\left[H g I_{4}\right] \Longrightarrow 2 K^{+}+\left[H g I_{4}\right]^{2-}$ Therefore, the osmotic pressure increases.
Q. Give one example each of miscible liquid pairs showing positive and negative deviations from Raoult’s law. Give one reason each for such deviations. [Delhi 2000; AI 2000]
Ans. Ethanol and water, methanol and $H_{2} O$ show positive deviation from Raoult's law because force of attraction between them decreases on mixing. and and, show negative deviation from Raoult's law because force of attraction between them increases on mixing.
Q. “The solution of a non-volatile solute boils at a higher temperature than the pure solvent.” Show this relationship on a graphic diagram. [AI 2002 C]
Ans. The diagram shows that solution containing non-volatile solute boils at temperature $T_{2}$ which is higher than boiling point of pure solvent, i.e., $T_{1}$
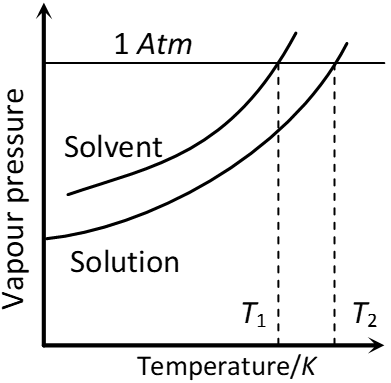
Variation of vapour pressure with Temperature showing boiling point of solution is higher than that of pure solvent.
Q. Carbon tetrachloride and water are immiscible whereas ethanol and water are miscible in all proportions. Correlate this behaviour with molecular structures of these compounds. [AI 2003]
Ans. Carbon tetrachloride is a non-polar compounds, it cannot form $H$ -bond with water, that is why $C C l_{4}$ and water do not mix with each other. Ethanol is a polar compound and $H_{2} \mathrm{O}$ is polar solvent, there is $H$ -bond between ethanol and water, therefore, ethanol and water are miscible in all proportions.
Q. Calculate molarity and molality of a $13 \%$ solution (by weight) of sulphuric acid? Its density is $1.020 \mathrm{g} \mathrm{cm}^{-3}$ (Atomic mass $H=1, O=16, S=32 \text { a. } m . u .)$ [Foreign 1999]
Ans. $M=\frac{w_{B}}{M_{B}} \times \frac{1000}{w_{A}}=\frac{13 \times 1000}{98 \times \frac{100}{1.02}}=\frac{13 \times 10 \times 1.02}{98}=\frac{1326}{98}$ $=1.353 \mathrm{mol} L^{-1}$ or $1.353 \mathrm{M}$ $m=\frac{w_{B}}{M_{B}} \times \frac{100}{w_{A}}=\frac{13}{98} \times \frac{1000}{87}=1.524 \mathrm{mol} / \mathrm{kg}_{\mathrm{or}} 1.524 \mathrm{m}$
Q. A solution is prepared by adding 60 g of methyl alcohol to 120 g of water. Calculate the mole fraction of methanol and water. [H.P. 1995]
Ans. Mass of methanol = 60 g Moles of methanol $\left.=\frac{60}{32}=1.875 \text { (Molar mass }=32\right)$ Moles of water $=\frac{120}{18}=6.667$ Total No. of moles = 1.875 + 6.667 = 8.542 Mole fraction of methanol $=\frac{1.875}{8.542}=0.220$ Mole fraction of water $=\frac{6.667}{8.542}=0.780$
Q. Vapour pressure of pure water at $35^{\circ} \mathrm{C}$ is $31.82 \mathrm{mm} \mathrm{Hg}$. When $27.0 \mathrm{g}$ of solute is dissolved in $100 \mathrm{g}$ of water (at the same temperature) vapour pressure of the solution thus formed is $30.95 \mathrm{mm}$ Hg. Calculate the molecular mass of the solute.
Ans. $\frac{P_{A}^{\circ}-P_{A}}{P_{A}^{\circ}}=X_{B} \Rightarrow \frac{31.82-30.95}{31.82}=\frac{27 / M}{100 / 18}$ $\Rightarrow \frac{0.87}{31.82}=\frac{27}{M_{B}} \times \frac{18}{100} \Rightarrow M_{B}=\frac{27 \times 18 \times 31.82}{0.87 \times 100}$ $\Rightarrow 177.75 g \mathrm{mol}^{-1}$
Q. In a solution of urea, $3.0 g$ of it is dissolved in $100 \mathrm{ml}$ of water. What will be the freezing point of this solution? State the approximation made if any. $\left[k_{f} \text { for water }=1.86 \mathrm{K} \mathrm{kg} \mathrm{mol}^{-1}, \text { molar mass of urea }=60 \mathrm{g}\right.$ $\left.m o l^{-1}\right]$ [Delhi 2002 C]
Ans. $\Delta T_{f}=k_{f} \times m$ $\Delta T_{f}=1.86 \times \frac{W_{B}}{M_{B}} \times \frac{1000}{W_{A}}=\frac{1.86 \times 3}{60} \times \frac{1000}{100}=0.93$ Freezing point of solution $=273 K-0.93=272.07 K$
Q. Give one example each of miscible liquid pairs showing positive and negative deviation from Raoults law. give one reason each for such deviations. [CBSE 2004]
Ans. Solution of $n$ hexane and ethanol shows positive deviations from Raoults law because $n$ -hexane molecular weaken the H-bonds between ethanol molecules which increases its vapour
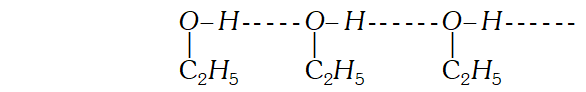
Solution of acetone and chloroform shows negative deviations from Raoult's law because of the formation of the $H$ -bonds between acetone and chloroform molecules.
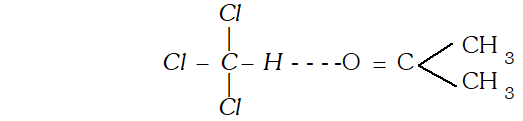
Q. What is meant by abnormal molecular mass of solute ? Discuss the factors, which bring abnormality in the experimentally determined molecular masses of solutes using colligative properties. [AI 1999 C]
Ans. The molecular mass obtained with the help of colligative property sometimes is different from normal molecular mass, it is called abnormal molecular mass. The factor which bring abnormality are (i) Association : When solute particles undergo association, number of particles become less and molecular mass determined with the help of colligative property will be more. (ii) Dissociation : It leads to increase in number of particles, therefore, increase in colligative property, therefore, therefore, decrease in molecular weight because colligative property is inversely proportional to molecular weight.
Q. Explain why vapour pressure of solvent is lowered by addition of a non-volative solute ?
Ans. It is observed that the presence of a non-volatile solute in a solution reduces the escaping tendency of solvent molecules into vapour phase. It is because some of the solute particles occupy the position of the solvent molecules on the liquid surface and thus dower the vapour pressure of the solvent.
Q. Ristinguish between ideal and non ideal solutions. [MP 2001, 02, 06]
Ans. 
Q. How will you determine the molecular mass of a substance by osmotic pressure method ?
Ans. According to Van’t Hoff equation $\pi v=n R T$ .....(i) $\pi=$ osmotic pressure; $T=$ Temperature for a solution If $w$ gram of solute is dissolved in $v$ litres of he solution and $M$ is the molecular mass of the solute, then $n=\frac{w}{M}$ Substituting this value in equation (v) we get, $\pi v=\frac{w}{M} R T \Rightarrow M=\frac{w R T}{\pi v}$ .....(ii) Thus, measuring the osmotic pressure of a solution containing grams of the solute in litres of the solution, at temperature the molecular man, of the solute can be calculated using equation (ii).
Q. The vapour pressure of pure liquid $A$ and $B$ are $70 \mathrm{mm}$ and $90 \mathrm{mm}$ Hg respectively at $25^{\circ} .$ The mole fraction of ^{ } $A^{\prime}$ in a solution of the two is $0.3 .$ Assuming that $A$ and $B$ form an ideal solution, calculate the partial pressure of each component in equilibrium with the solution. [AI 1999 C]
Ans. 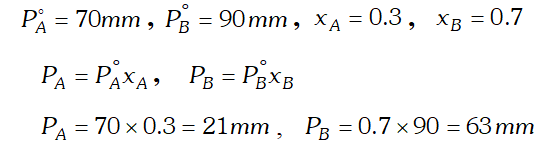
Q. Assuming complete dissociation, calculate the expected freezing point of a solution prepared by dissolving $6.00 \mathrm{g}$ Glaubers salt, $N a_{2} S O_{4}, 10 H_{2} O$ in. 100 kg of $H_{2} O\left[K_{f}=1.86\right.$ $\left.K \mathrm{kg} \mathrm{mol}^{-1}\right)$ [CBSE Board 1998]
Ans. 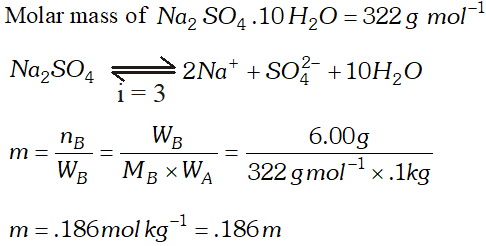
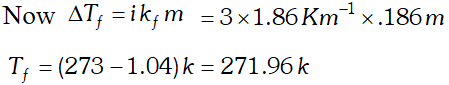
Q. $2 \mathrm{g}$ of $\mathrm{C}_{6} \mathrm{H}_{5} \mathrm{COOH}$ dissolved in $25 \mathrm{g}$ of benzene shows a depression in freezing point equal to $1.62 \mathrm{K} .$ Molar depression constant for benzene is $4.9 \mathrm{K} \mathrm{kg} \mathrm{mol}^{-1} .$ What is the percentage association of acid if it exists as dimer in solution. [CBSE 2004]
Ans. Here $W_{A}=25 g, W_{b}=2 g, \Delta T_{f}=1.62 K, K_{f}=4.9 K \mathrm{kg} \mathrm{mol}^{-1}$ Observed molecular mass of benzoic acid, $M_{B}=\frac{1000 K_{f} \times W_{B}}{\Delta T_{f} \times W_{A}}=\frac{1000 \times 4.9 \times 2}{1.62 \times 25}=242$ Calculated molecular mass of benzoic acid $=72+5+12+32+1=122$ Van't Hoff factor $i=\frac{\text { Calculated molecular mass }}{\text { Observed molecular mass }}=\frac{122}{242}=.504$ Let $\alpha$ be the degree of dissociation \[ 2 C_{6} H_{5} C O O H \rightleftharpoons\left(C_{6} H_{5} C O O H\right)_{2} \]
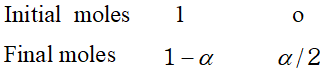
Total number of moles after association $=1-\alpha+\frac{\alpha}{2}=1-\frac{\alpha}{2}$ $\therefore \quad i=\frac{1-\frac{\alpha}{2}}{1}=.504$ or $\quad \alpha=(1-.504) \times 2=.496 \times 2=.992$ percentage of association $=99.2 \%$
Q. With the help of a simple diagram, describe Berkeley and Hartley’s method of determining the osmotic pressure of a dilute solution. [MP 2002, 04, 06]
Ans. Experimental Measurement of Osmotic Pressure. A number of methods are available for measurement of osmotic pressure. The best out of these is Berkeley and Hartley’s Method. This method is based upon applying pressure on the solution which is just sufficient to prevent the entry of the solvent into the solution through the semi-permeable membrane. The apparatus used by Berkeley and nartley is shown in Figure. It consists of a porous tube (open at both ends) containing the semi-permeable membrance of copper ferrocyanide. The porous tube is fitted with a reservoir R on one side and a tube T on the other. The porous tube is filled with the pure solvent so that the level in the tube T stands at the mark M. The porous tube is fitted into an outer vessel made of gun metal. This vessel has a wide tube at the top which is fitted with a frictionless piston and a pressure gauge as shown in figure. The solution under study is taken in the outer gun metal vessel. As a result of osmosis, the level in the tube tends to fall. The pressure applied on the solution by means of the piston which keeps the level in the tube at is a measure of the osmotic pressure and can be read directly on the pressure gauge. This method is superior to the other methods because of the following reasons :
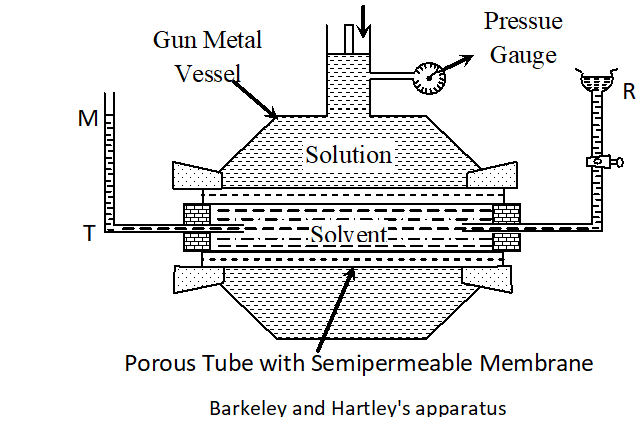
(a) In this method, the osmotic pressure is balanced by the external pressure so that there is no strain on the membrane. (b) The concentration of the solution does not change because the entry of the solvent into the solution is prevented by the external pressure. (c) The time taken for the measurement of osmotic pressure is much less in this method as compared to the other methods.
Q. Draw a suitable labelled diagram to express the relationships for ideal solution of A and B between vapour pressure and mole fractions of components at constant temperature. [CBSE 2002; Delhi 2002]
Ans. 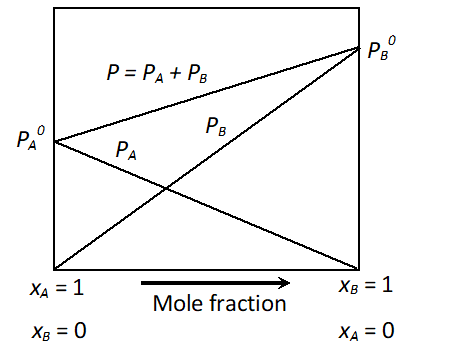
Relationships between V.P. and mole fraction for ideal solution
Q. $2 g$ of benzoic acid $\left(C_{6} H_{5} C O O H\right)$ dissolved in $25 g$ of benzene shows a depression in freezing point equal to $1.62 K .$ Molal depression constant for benzene is $4.9 K$ $k g \mathrm{mol}^{-1} .$ What is the percentage association of acid if it forms dimer in solution?
Ans. The given quantities are : $w_{2}=2 g ; K_{f}=4.9 \mathrm{K} \mathrm{kg} \mathrm{mol}^{-1}$ ; $w_{1}=25 g, \Delta T_{f}=1.62 K$ Substituting these values in equation $M_{2}=\frac{k_{f} \times w_{2} \times 1000}{\Delta T_{f} \times w_{1}}$ $M_{2}=\frac{4.9 \mathrm{K} \mathrm{kg} \mathrm{mol}^{-1} \times 2 \mathrm{g} \times 1000 \mathrm{g} \mathrm{kg}^{-1}}{25 \mathrm{g} \times 1.62 \mathrm{K}}=241.98 \mathrm{gmol}^{-1}$ Thus, experimental molar mass of benzoic acid in benzene is $=241.98 \mathrm{g} \mathrm{mol}^{-1}$ Now consider the following equilibrium for the acid: $2 \mathrm{C}_{6} \mathrm{H}_{5} \mathrm{COOH}$ BHA $\left(\mathrm{C}_{6} \mathrm{H}_{5} \mathrm{COOH}\right)_{2}$ If $x$ represents the degree of association of the solute then we would have $(1-x)$ mol of benzoic acid left in unassociated form and correspondingly $\frac{x}{2}$ as associated moles of benzoic acid at equilibrium. Therefore, total number of moles of particles at equilibrium is: $1-x+\frac{x}{2}=1-\frac{x}{2}$ Thus, total number of moles of particles at equilibrium equals Van't Hoff factor $i$ But $i=\frac{\text { Normal molar mass }}{\text { Abnormal molar mass }}=\frac{122 g \mathrm{mol}^{-1}}{241.98 \mathrm{gmol}^{-1}}$ $\Rightarrow \frac{x}{2}=1-\frac{122}{241.98}=1-0.504=0.496$ $\Rightarrow x=2 \times 0.496=0.992$ Therefore, degree of association of benzoic acid in benzene is $99.2 \%$
 Variation of vapour pressure with Temperature showing boiling point of solution is higher than that of pure solvent.
Variation of vapour pressure with Temperature showing boiling point of solution is higher than that of pure solvent. 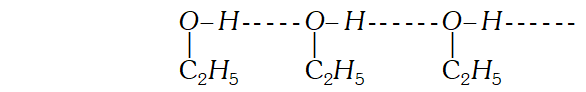 Solution of acetone and chloroform shows negative deviations from Raoult's law because of the formation of the $H$ -bonds between acetone and chloroform molecules.
Solution of acetone and chloroform shows negative deviations from Raoult's law because of the formation of the $H$ -bonds between acetone and chloroform molecules. 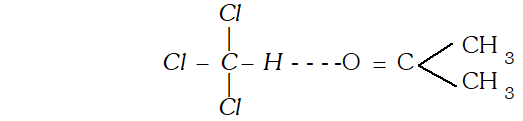

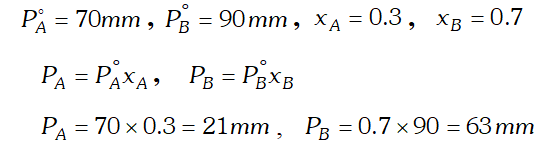
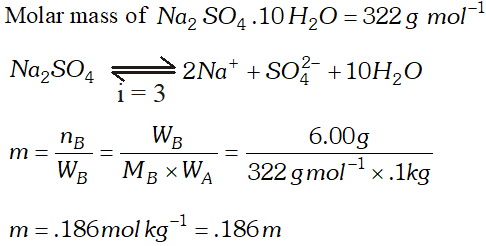
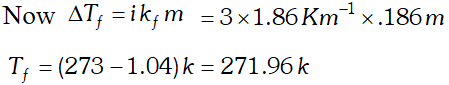
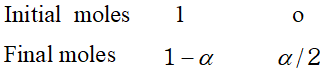 Total number of moles after association $=1-\alpha+\frac{\alpha}{2}=1-\frac{\alpha}{2}$ $\therefore \quad i=\frac{1-\frac{\alpha}{2}}{1}=.504$ or $\quad \alpha=(1-.504) \times 2=.496 \times 2=.992$ percentage of association $=99.2 \%$
Total number of moles after association $=1-\alpha+\frac{\alpha}{2}=1-\frac{\alpha}{2}$ $\therefore \quad i=\frac{1-\frac{\alpha}{2}}{1}=.504$ or $\quad \alpha=(1-.504) \times 2=.496 \times 2=.992$ percentage of association $=99.2 \%$  (a) In this method, the osmotic pressure is balanced by the external pressure so that there is no strain on the membrane. (b) The concentration of the solution does not change because the entry of the solvent into the solution is prevented by the external pressure. (c) The time taken for the measurement of osmotic pressure is much less in this method as compared to the other methods.
(a) In this method, the osmotic pressure is balanced by the external pressure so that there is no strain on the membrane. (b) The concentration of the solution does not change because the entry of the solvent into the solution is prevented by the external pressure. (c) The time taken for the measurement of osmotic pressure is much less in this method as compared to the other methods.  Relationships between V.P. and mole fraction for ideal solution
Relationships between V.P. and mole fraction for ideal solution 