JEE Advanced Previous Year Questions of Physics with Solutions are available at eSaral. Practicing JEE Advanced Previous Year Papers Questions of Physics will help the JEE aspirants in realizing the question pattern as well as help in analyzing weak & strong areas.
Get detailed Class 11th & 12th Physics Notes to prepare for Boards as well as competitive exams like IIT JEE, NEET etc.
eSaral helps the students in clearing and understanding each topic in a better way. eSaral is providing complete chapter-wise notes of Class 11th and 12th both for all subjects.
Click Here for JEE main Previous Year Topic Wise Questions of Physics with Solutions
Download eSaral app for free study material and video tutorials.
Simulator
Previous Years JEE Advanced Questions
Q. A police car with a siren of frequency 8 kHz is moving with uniform velocity 36 km/hr towards a tall building which reflects the sound waves. The speed of sound in air is 320 m/s. The frequency of the siren heard by the car driver is ?
(A) 8.50 kHz (B) 8.25 kHz (C) 7.75 kHz (D) 7.50 kHz
[JEE 2011]
Ans. (A)
$f^{\prime}=\left(\frac{v}{v-v_{s}}\right)\left(\frac{v+v_{0}}{v}\right) f \Rightarrow f^{\prime}=\left(\frac{320}{320-10}\right)\left(\frac{320+10}{320}\right) \times 8 \Rightarrow f^{\prime} \approx 8.50 \mathrm{kHz}$
Q. Column-I shows four systems, each of the same length L, for producing standing waves. The lowest possible natural frequency of a system is called its fundamental frequency, whose wavelength is denoted as $\lambda_{\mathrm{f}}$. Match each system with statements given in Column-II describing the nature and wavelength of the standing waves.
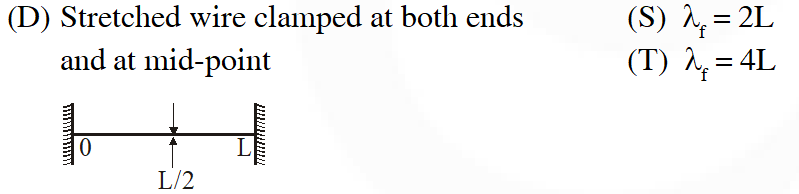[JEE 2011]
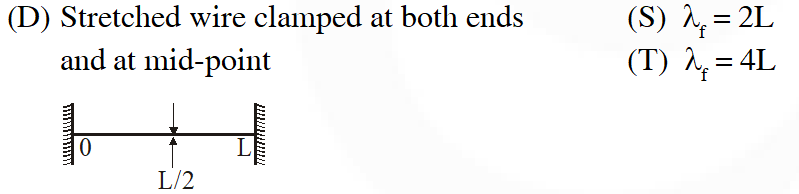[JEE 2011]
Ans. ((A) $\mathrm{P}, \mathrm{T}(\mathrm{B}) \mathrm{P}, \mathrm{S}(\mathrm{C}) \mathrm{Q}, \mathrm{S}(\mathrm{D}) \mathrm{Q}, \mathrm{R}$)
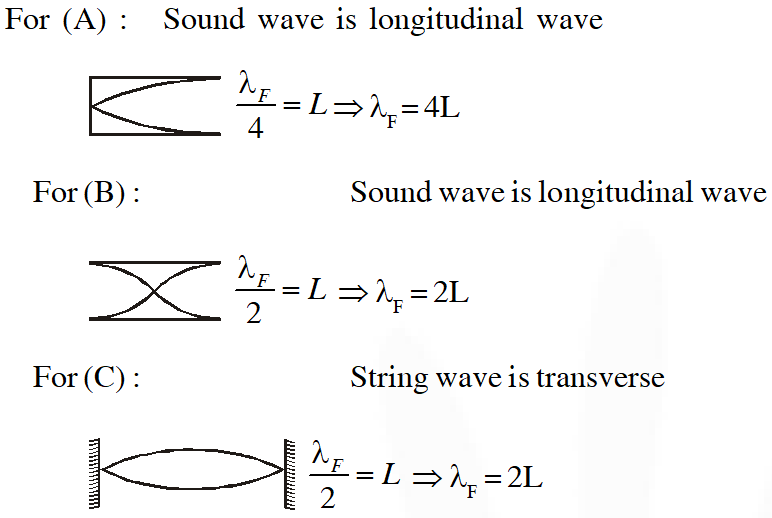
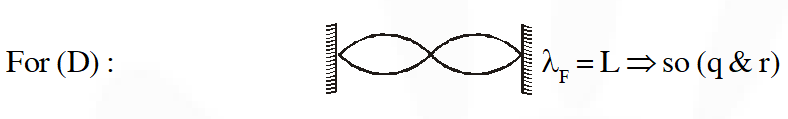
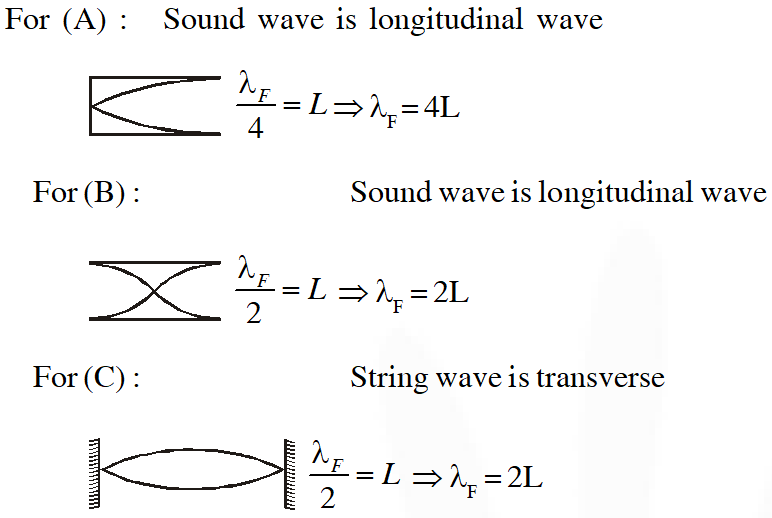
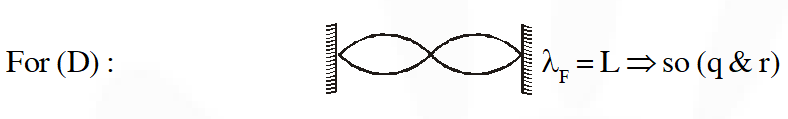
Q. A person blows into open-end of a long pipe. As a result, a high-pressure pulse of air travels down the pipe. When this pulse reaches the other end of the pipe.
(A) a high-pressure pulse starts travelling up the pipe, if the other end of the pipe is open
(B) a low -pressure pulse starts travelling up the pipe, if the other end of the pipe is open
(C) a low pressure pulse starts travelling up the pipe, if the other end of the pipe is closed
(D) a high-pressure pulse starts travelling up the pipe, if the other end of the pipe is closed
[JEE 2012]
Ans. ($\mathrm{B}, \mathrm{D}$)
Information Based (Refer NCERT)
Q. A student is performing the experiment of Resonance Column. The diameter of the column tube is 4 cm. The frequency of the tuning fork is 512 Hz. The air temperature is $38^{\circ} \mathrm{C}$in which the speed of sound is 336 m/s. The zero of the meter scale coincides with the top end of the Resonance column tube. When the first resonance occurs, the reading of the water level in the column is :-
(A) 14.0 cm (B) 15.2 cm (C) 16.4 cm (D) 17.6 cm
[JEE 2012]
Ans. (B)
In resonance column experiment $\frac{\lambda}{4}=\ell_{1}+e$ so, $\ell_{1}=\frac{\lambda}{4}-e=\frac{v}{4 f}-0.3 d$
$=\frac{336 \times 100 \mathrm{cm}}{4 \times 512}-(0.3)(4 \mathrm{cm})=16.4-1.2=15.2 \mathrm{cm}$
Q. A student is performing an experiment using a resonance column and a tuning fork of frequency
$244 \mathrm{s}^{-1}$ . He is told that the air in the tube has been replaced by another gas (assume that the column remains filled with the gas). If the minimum height at which resonance occurs is (0.350 $\pm 0.005)$ m, the gas in the tube is
(Useful information $: \sqrt{167 \mathrm{RT}}=640 \mathrm{J}^{1 / 2}$ mole $^{-1 / 2} ; \sqrt{140 \mathrm{RT}}=590 \mathrm{J}^{1 / 2}$ mole $^{-1 / 2} .$ The molar masses M in grams are given in the options. Take the values of $\sqrt{\frac{10}{\mathrm{M}}}$ for each gas as given there. )
(A) Neon $\left(\mathrm{M}=20, \sqrt{\frac{10}{20}}=\frac{7}{10}\right)$
(B) Nitrogen $\left(\mathrm{M}=28, \sqrt{\frac{10}{28}}=\frac{3}{5}\right)$
(C) Oxygen $\left(\mathrm{M}=32, \sqrt{\frac{10}{32}}=\frac{9}{16}\right)$
(D) Argon $\left(\mathrm{M}=36, \sqrt{\frac{10}{36}}=\frac{17}{32}\right)$
[JEE Advanced-2014]
Ans. (D)
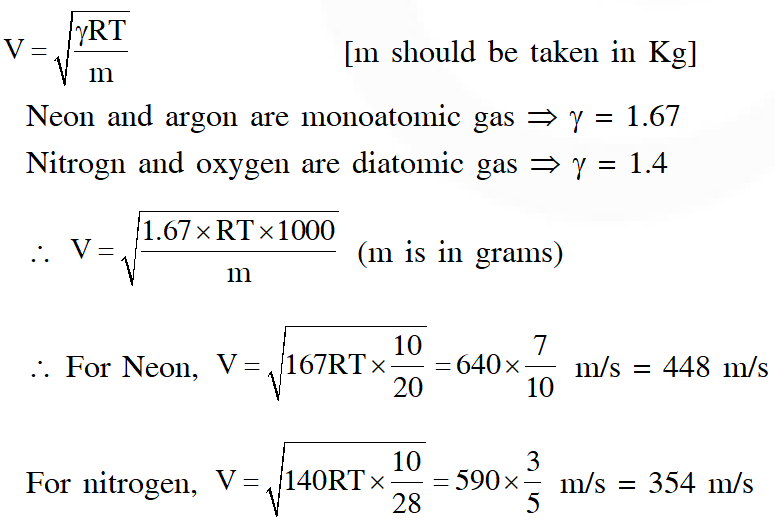
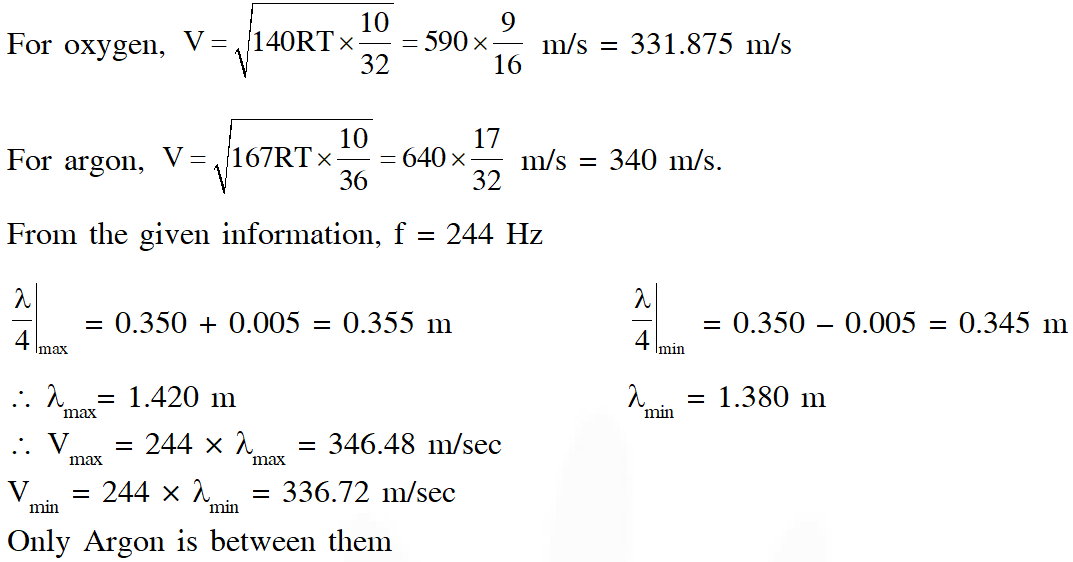
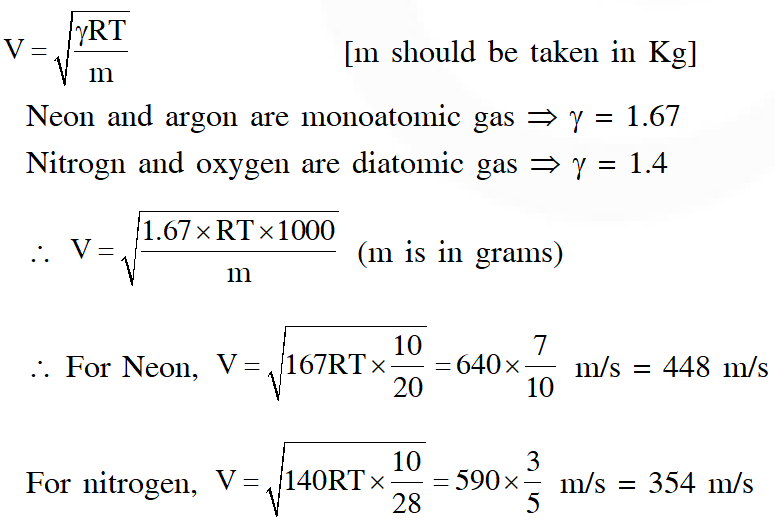
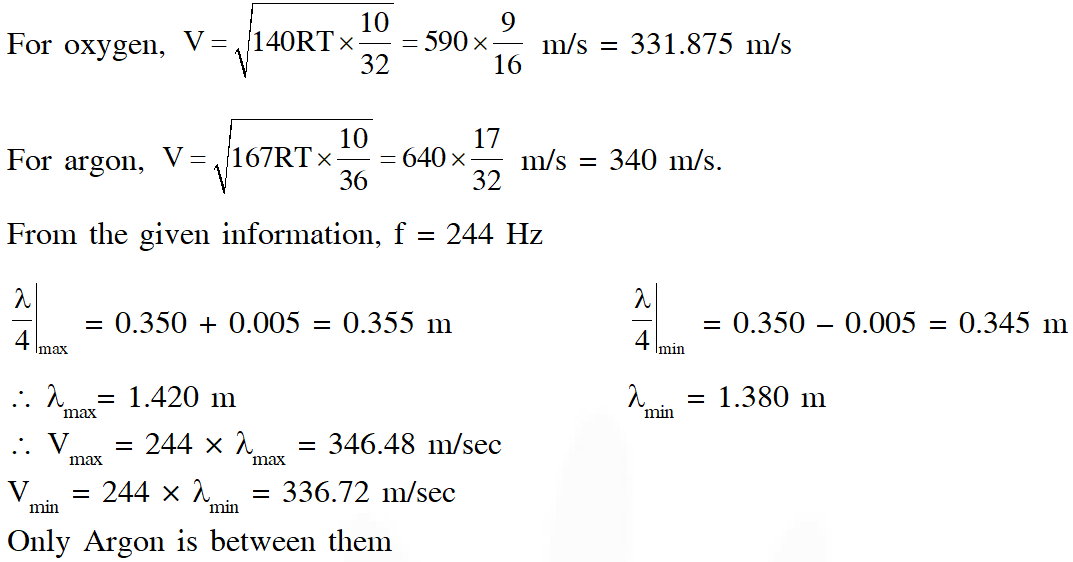
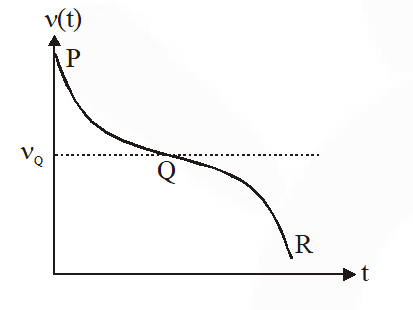
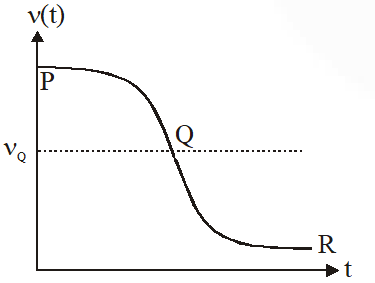
Q. Two loudspeakers M and N are located 20m apart and emit sound at frequencies 118 Hz and 121 Hz, respectively. A car is initially at a point P, 1800 m away from the midpoint Q of the line MN and moves towards Q constantly at 60 km/hr along the perpendicular bisector of MN. It crosses Q and eventually reaches a point R, 1800 m away from Q. Let n(t) represent the beat frequency measured by a person sitting in the car at time t. Let $v_{\mathrm{p}}, v_{\mathrm{Q}}$ and $v_{\mathrm{R}}$ be the beat frequencies measured at locations P, Q and R, respectively. The speed of sound in air is 330 $\mathrm{ms}^{-1}$. Which of the following statement(s) is(are) true regarding the sound heard by the person ?
(A) The plot below represents schematically the variation of beat frequency with time
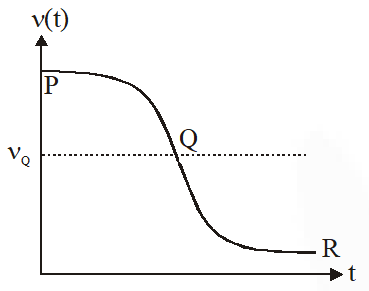(B) The plot below represents schematically the variations of beat frequency with time
(C) The rate of change in beat frequency is maximum when the car passes through Q
(D) $v_{\mathrm{p}}+v_{\mathrm{R}}=2 v_{\mathrm{Q}}$
[JEE Advanced 2016]
(B) The plot below represents schematically the variations of beat frequency with time
(C) The rate of change in beat frequency is maximum when the car passes through Q
(D) $v_{\mathrm{p}}+v_{\mathrm{R}}=2 v_{\mathrm{Q}}$
[JEE Advanced 2016]
Ans. (A,C,D)
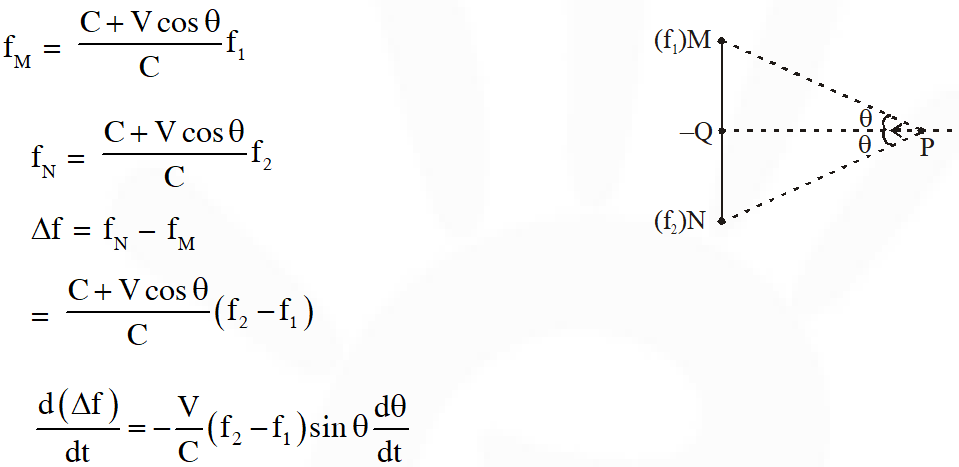
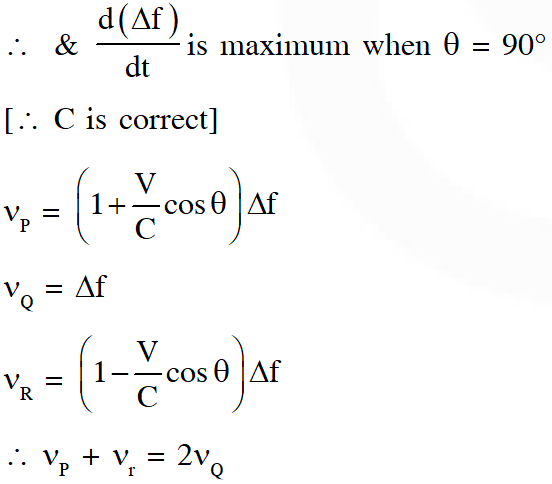
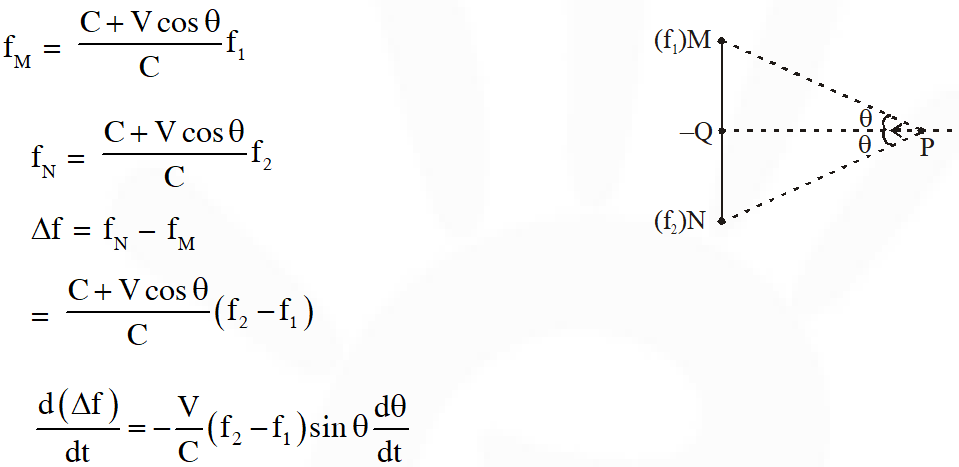
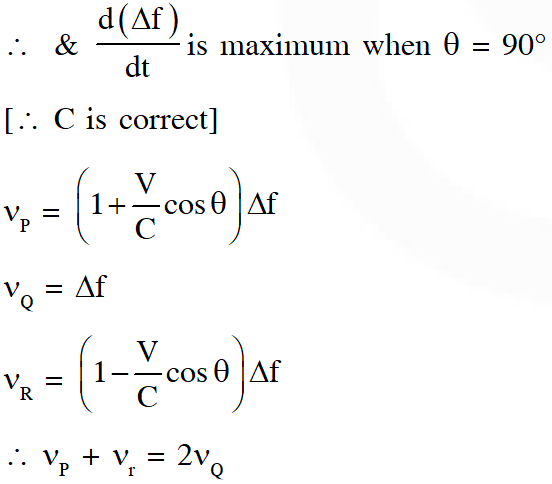
Q. A stationary source emits sound of frequency $\mathrm{f}_{0}=492 \mathrm{Hz}$ . The sound is reflected by a large car approaching the source with a speed of $2 \mathrm{ms}^{-1}$. The reflected signal is received by the source and superposed with the original. What will be the beat frequency of the resulting signal in Hz ? (Given that the speed of sound in air is 330 $\mathrm{ms}^{-1}$ and the car reflects the sound at the frequency it has received).
[JEE Advanced 2017]
Ans. 6
Frequency of sound as received by large car approaching the source.
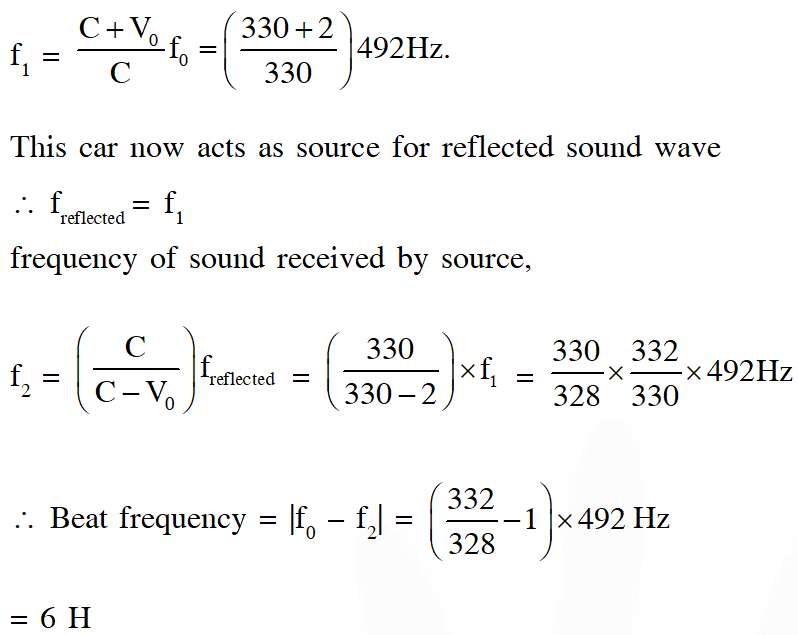
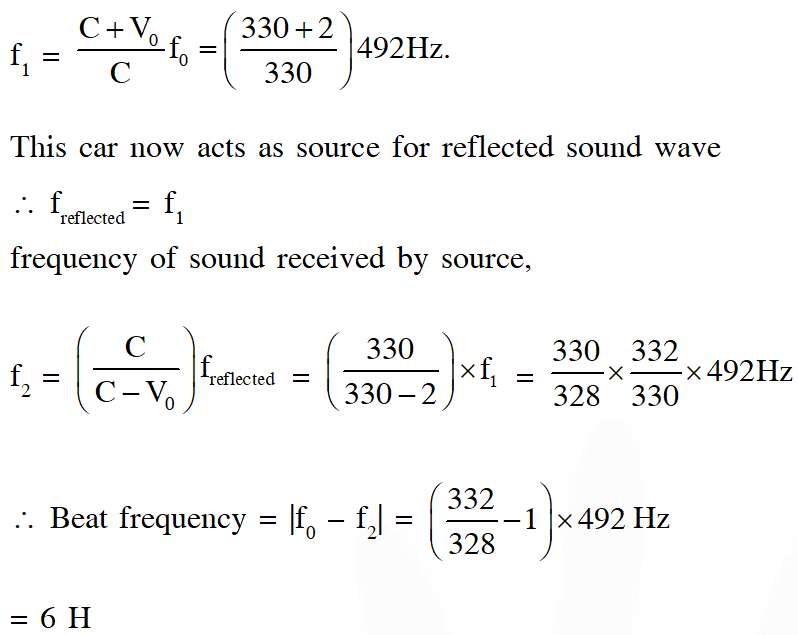
Q. Two men are walking along a horizontal straight line in the same direction. The man in front walks at a speed 1.0 $\mathrm{ms}^{-1}$ and the man behind walks at a speed 2.0 $\mathrm{ms}^{-1}$. A third man is standing at a height 12 m above the same horizontal line such that all three men are in a vertical plane. The two walking men are blowing identical whistles which emit a sound of frequency 1430 Hz. The speed of sound in air is 330 $\mathrm{ms}^{-1}$. At the instant, when the moving men are 10 m apart, the stationary man is equidistant from them. The frequency of beats in Hz, heard by the stationary man at this instant, is _____
[JEE Advanced 2018]
Ans. 5.00 Hz
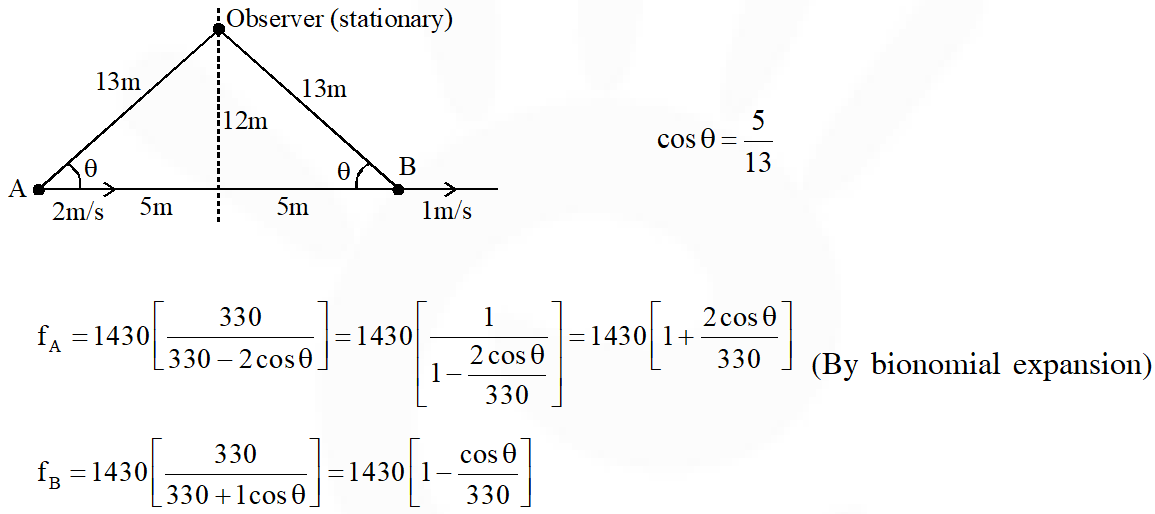
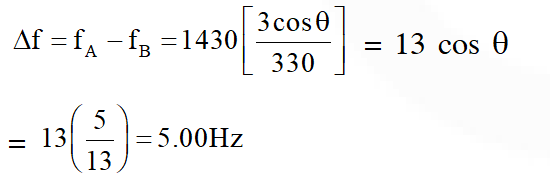
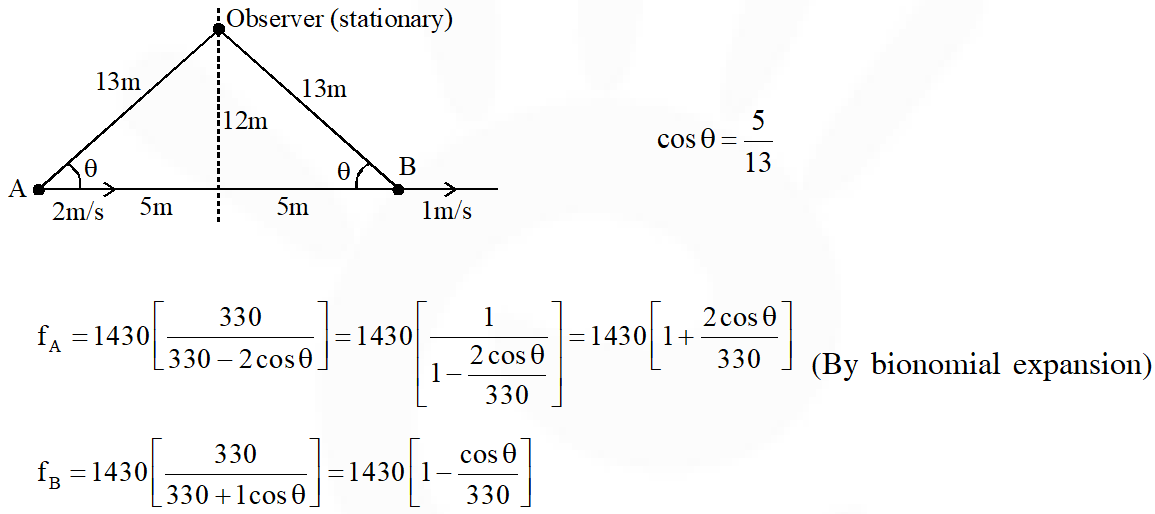
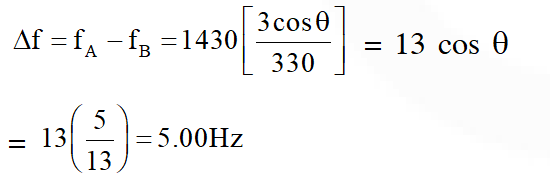
Q. In an experment to measure the speed of sound by a resonating air column, a tuning fork of frequency 500 Hz is used. The length of the air column is varied by changing the level of water in the resonance tube. Two successive resonances are heard at air columns of length 50.7 cm and 83.9 cm. Which of the following statements is (are) true ?
(A) The speed of sound determined from this experiment is $332 \mathrm{ms}^{-1}$
(B) The end correction in this experiment is 0.9 cm
(C) The wavelength of the sound wave is 66.4 cm
(D) The resonance at 50.7 cm corresponds to the fundamental harmonic
[JEE Advanced 2018]
Ans. (A,C)
Let $\mathrm{n}_{1}$ harmonic is corresponding to 50.7 cm & $\mathrm{n}_{2}$ harmonic is corresponding 83.9 cm. since both one consecutive harmonics.
$\therefore$ their difference $=\frac{\lambda}{2}$
$\therefore \frac{\lambda}{2}=(83.9-50.7) \mathrm{cm}$
$\frac{\lambda}{2}=33.2 \mathrm{cm}$
$\lambda=66.4 \mathrm{cm}$
$\therefore \frac{\lambda}{4}=16.6 \mathrm{cm}$
length corresponding to fundamental mode must be close to \frac{\lambda}{4} \& 50.7 cm must be an odd multiple of this length 16.6 × 3 = 49.8 cm. therefore 50.7 is 3^{| \mathrm{rd}}harmonic
If end correction is e, then
\mathrm{e}+50.7=\frac{3 \lambda}{4}
\mathrm{e}=49.8-50.7=-0.9 \mathrm{cm}
\text { speed of sound, } \mathrm{v}=\mathrm{f} \lambda
\therefore \mathrm{v}=500 \times 66.4 \mathrm{cm} / \mathrm{sec}=332.000 \mathrm{m} / \mathrm{s}