JEE Main Previous Year Question of Physics with Solutions are available here. Practicing JEE Main Previous Year Papers Questions of Physics will help all the JEE aspirants in realizing the question pattern as well as help in analyzing their weak & strong areas.
Get detailed Class 11th &12th Physics Notes to prepare for Boards as well as competitive exams like IIT JEE, NEET etc.
eSaral helps the students in clearing and understanding each topic in a better way. eSaral is providing complete chapter-wise notes of Class 11th and 12th both for all subjects.
Besides this, eSaral also offers NCERT Solutions, Previous year questions for JEE Main and Advance, Practice questions, Test Series for JEE Main, JEE Advanced and NEET, Important questions of Physics, Chemistry, Math, and Biology and many more.
Download eSaral app for free study material and video tutorials.
Q. Three sound waves of equal amplitudes have frequencies (–1), , (+1). They superpose to give beats. The number of beats produced per second will be :-
(1) 2 (2) 1 (3) 4 (4) 3
[AIEEE - 2009]
Ans. (1)
Q. A motor cycle starts from rest and accelerates along a straight path at 2 \mathrm{m} / \mathrm{s}^{2}. At the starting point of the motor cycle there is a stationary electric siren. How far has the motor cycle gone when the driver hears the frequency of the siren at 94% of its value when the motor cycle was at rest ? (Speed of sound = 330 \mathrm{ms}^{-1}) :-
(1) 147 m (2) 196 m (3) 49 m (4) 98 m
[AIEEE - 2009]
Ans. (4)
$n^{\prime}=\frac{v-v_{0}}{v} n=\frac{94}{100} n$
from (iii) eq". of motion $v^{2}=u^{2}+2 a s$
$\Rightarrow \mathrm{v}_{0}^{2}=0+2 \mathrm{as} \Rightarrow \mathrm{v}_{0}=\sqrt{2 \mathrm{as}}$
$\Rightarrow \frac{94}{100} \mathrm{n}=\left(\frac{\mathrm{v}-\sqrt{2 \mathrm{as}}}{\mathrm{v}}\right) \mathrm{n} \Rightarrow \mathrm{s}=98 \mathrm{m}$
Q. A pipe of length 85 cm is closed from one end. Find the number of possible natural oscillations of air column in the pipe whose frequencies lie below 1250 Hz. The velocity of sound in air is
340 m/s.
(1) 6 (2) 4 (3) 12 (4) 8
[JEE Mains - 2014]
Ans. (1)
Fundamental frequency of closed organ pipe
$\mathrm{f}_{0}=\frac{\mathrm{v}}{4 \ell}=\frac{340}{4 \times 0.85}=100 \mathrm{Hz}$
So possible frequencies below 1250 Hz are
100 Hz, 300 Hz, 500 Hz, 700 Hz, 900 Hz,
1100 Hz
$\Rightarrow$ No. of frequencies $=6$
Q. A train is moving on a straight track with speed 20 \mathrm{ms}^{-1}. It is blowing its whistle at the frequency of 1000 Hz. The percentage change in the frequency heard by a person standing near the track as the train passes him is (speed of sound = 320 \mathrm{ms}^{-1}) close to :-
(1) 18% (2) 24% (3) 6% (4) 12%
[JEE Mains - 2015]
Ans. (4)
$\mathrm{f}^{\prime}=\mathrm{f}\left(\frac{\mathrm{v}}{\mathrm{v}-\mathrm{v}_{\mathrm{s}}}\right)$
$\mathrm{f}^{\prime \prime}=\mathrm{f}\left(\frac{\mathrm{v}}{\mathrm{v}+\mathrm{v}_{\mathrm{s}}}\right)$
$\frac{\mathrm{f}^{\prime \prime}}{\mathrm{f}^{\prime}}=\frac{\mathrm{v}-\mathrm{v}_{\mathrm{S}}}{\mathrm{v}+\mathrm{v}_{\mathrm{S}}}$
$\frac{\mathrm{f}^{\prime \prime}-\mathrm{f}^{\prime}}{\mathrm{f}^{\prime}} \times 100=\frac{\mathrm{v}-\mathrm{v}_{\mathrm{S}}-\mathrm{v}-\mathrm{v}_{\mathrm{S}}}{\mathrm{v}+\mathrm{v}_{\mathrm{S}}} \times 10$
$=-\frac{2 \mathrm{v}_{\mathrm{S}}}{\mathrm{v}+\mathrm{v}_{\mathrm{S}}}=-\frac{2}{1+\frac{\mathrm{v}}{\mathrm{v}_{\mathrm{S}}}} \times 100 \simeq 12 \%$
Q. An observer is moving with half the speed of light towards a stationary microwave source emitting waves at frequency 10 GHz. What is the frequency of the microwave measured by the observer?
(speed of light $=3 \times 10^{8} \mathrm{ms}^{-1}$ )
(1) 17.3 GHz
(2) 15.3 GHz
(3) 10.1 GHz
(4) 12.1 GHz
[JEE Mains - 2017]
Ans. (1)
Doppler effect in light (speed of observer is not very small compare to speed of light)
$\mathrm{f}^{1}=\sqrt{\frac{1+\mathrm{V} / \mathrm{C}}{1-\mathrm{V} / \mathrm{C}}} \mathrm{f}_{\mathrm{source}}=\sqrt{\frac{1+1 / 2}{1-1 / 2}}(10 \mathrm{GHz})$
= 17.3 GHz
Q. A granite rod of 60 cm length is clamped at its middle point and is set into longitudinal vibrations. The density of granite is $2.7 \times 10^{3} \mathrm{kg} / \mathrm{m}^{3}$ and its Young's modulus is $9.27 \times 10^{10}$ Pa. What will be the fundamental frequency of the longitudinal vibrations ?
(1) 2.5 kHz
(2) 10 kHz
(3) 7.5 kHz
(4) 5 kHz
[JEE Mains - 2018]
Ans. (4)
Velocity of wave $=\sqrt{\frac{\mathrm{Y}}{\rho}}$
$=\sqrt{\frac{9.27 \times 10^{10}}{2.7 \times 10^{3}}}$
$=\sqrt{3.433 \times 10^{7}}$
$=10^{3} \times \sqrt{34.33}$
$\mathrm{v}_{\omega}=5.85 \times 10^{3} \mathrm{m} / \mathrm{sec}$
Since rod is clamped at middle fundamental wave shape is as follow
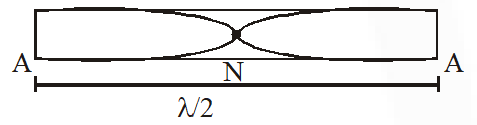$\frac{\lambda}{2}=\mathrm{L}$
$\lambda=2 \mathrm{L}$
$\mathrm{L}=60 \mathrm{cm}=0.6 \mathrm{m}(\mathrm{given})$
$\lambda=1.2 \mathrm{m}$
$\mathrm{v}=\mathrm{f} \lambda$
$\mathrm{f}=\frac{\mathrm{v}}{\lambda}=\frac{5.85 \times 10^{3}}{1.2}$
$=4.88 \times 10^{3} \mathrm{Hz} \square 5 \mathrm{KHz}$
$\frac{\lambda}{2}=\mathrm{L}$
$\lambda=2 \mathrm{L}$
$\mathrm{L}=60 \mathrm{cm}=0.6 \mathrm{m}(\mathrm{given})$
$\lambda=1.2 \mathrm{m}$
$\mathrm{v}=\mathrm{f} \lambda$
$\mathrm{f}=\frac{\mathrm{v}}{\lambda}=\frac{5.85 \times 10^{3}}{1.2}$
$=4.88 \times 10^{3} \mathrm{Hz} \square 5 \mathrm{KHz}$