Hey, do you want to learn how to State and explain Coulomb law? If yes. Then keep reading.

Coulomb's law

The force of attraction or repulsion between two stationary point charges is directly proportional to the product of charges and inversely proportional to the square of the distance between them. This force acts along the line joining the center of two charges.

If $q_{1} \& q_{2}$ are charges, r is the distance between them and F is the force acting between them

Then, $F \alpha q_{1} q_{2}$

$\mathrm{F} \alpha 1 / \mathrm{r}^{2}$

$\mathrm{F} \alpha \frac{\mathrm{q}_{1} \mathrm{q}_{2}}{\mathrm{r}^{2}}$

Or $\mathrm{F}=\mathrm{c} \frac{\mathrm{q}_{1} \mathrm{q}_{2}}{\mathrm{r}^{2}}$

C is const. which depends upon system of units and also on medium between two charges

$C=\frac{1}{4 \pi \varepsilon_{0}}=9 \times 10^{9} \mathrm{Nm}^{2} / \mathrm{C}^{2}$

(In SI unit)

C = 1 in electrostatic unit (esu)

$\varepsilon_{0}=8.85 \times 10^{-12} \mathrm{C}^{2} / \mathrm{Nm}^{2}$

= permittivity of free space or vacuum

Effect of medium

The dielectric constant of a medium is the ratio of the electrostatic force between two charges separated by a given distance in air to electrostatic force between same two charges separated by same distance in that medium.

$\mathrm{F}_{\text {air }}=\frac{1}{4 \pi \varepsilon_{0}} \frac{\mathrm{q}_{1} \mathrm{q}_{2}}{\mathrm{r}^{2}}$

And

$F_{\text {medium }}=\frac{1}{4 \pi \varepsilon_{0} \varepsilon_{\mathrm{r}}} \frac{\mathrm{q}_{1} \mathrm{q}_{2}}{\mathrm{r}^{2}}$

$\frac{F_{\text {medium }}}{\mathrm{F}_{\text {air }}}=\frac{1}{\varepsilon_{\mathrm{r}}}=\mathrm{K}$

$\varepsilon_{r}$ or $\mathrm{K}$ = Dielectric constant or Relative permittivity or specific inductive capacity of medium.

1. Permittivity: Permittivity is a measure of the ability of the medium surrounding electric charges to allow electric lines of force to pass through it. It determines the forces between the charges.
2. Relative Permittivity : The relative permittivity or the dielectric constant $\left(\varepsilon_{r}\right.$ or $\left.\mathrm{K}\right)$ of a medium is defined as the ratio of the permittivity $\varepsilon$ of the medium to the permittivity$\varepsilon_{0}$ of free space i.e.

$\varepsilon_{\mathrm{r}}$

Or

$\mathrm{K}=\frac{\varepsilon}{\varepsilon_{0}}$

Dimensions of permittivity

$\varepsilon_{0}=\frac{Q^{2}}{F \times \text { length }^{2}}$

$=\frac{T^{2} A^{2}}{M L T^{-2} L^{2}}$

$=M^{-1} L^{-3} T^{4} A^{2}$

The dielectric constants of different mediums are

Coulomb's law in vector form

The direction of the force acting between two charges depends on their nature and it is along the line joining the center of two charges.

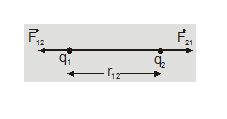
$\vec{F}_{21}=$ force on $q_{2}$ due to $q_{1}$

$\overrightarrow{F_{21}}=\frac{1}{4 \pi \varepsilon_{0} \varepsilon_{r}} \frac{q_{1} q_{2}}{r_{12}^{2}} \hat{r}_{12}$

$\overrightarrow{\mathrm{F}}_{12}=$ Force on $\mathrm{q}_{1}$ due to $\mathrm{q}_{2}$

$\overrightarrow{F_{12}}=\frac{1}{4 \pi \varepsilon_{0} \varepsilon_{r}} \frac{q_{1} q_{2}}{r_{21}^{2}} \hat{r}_{21}$

$\vec{F}_{12}=-\vec{F}_{21} \quad$ (as $\left.\hat{r}_{12}=-\hat{r}_{21}\right)$

Or

$\overrightarrow{\mathrm{F}}_{12}+\overrightarrow{\mathrm{F}}_{21}=0$

Important points

1. The electrostatic force is a medium-dependent force.
2. The electrostatic force is an action-reaction pair, i.e., the force exerted by one charge on the other is equal and opposite to the force exerted by the other on the first.
3. The force is conservative, i.e., work done in moving a point charge around a closed path under the action of Coulomb's force is zero.
4. Coulomb's law is applicable to point charges only. But it can be applied for distributed charges also.
5. This law is valid only for stationary point charges and cannot be applied for moving charges.
6. The law expresses the force between two-point charges at rest. In applying it to the case of extended bodies of finite size care should be taken in assuming the whole charge of a body to be concentrated at its 'center' as this is true only for the spherically charged body, that too for a external point.
7. The equilibrium of a charged particle under the action of coulombian forces alone can never be stable'. This statement is called Earnshaw's theorem.
8. Unit of charge $\mathrm{F}=\frac{1}{4 \pi \varepsilon_{0}} \frac{\mathrm{q}_{1} \mathrm{q}_{2}}{\mathrm{r}^{2}}$

If $q_{1}=q_{2}=1$ coulomb,

$r=1 m$

then $F=\frac{1}{4 \pi \varepsilon_{0}}=9 \times 10^{9}$ N

One coulomb of charge is that charge which when placed at rest in vacuum at a distance of one meter from an equal and similar stationary charge repels it and is repelled by it with a force of

$9 \times 10^{9}$ newton.

So, that's all from this article. I hope you get the idea about how to State and explain coulomb law. If you liked this article then please share it with your friends. If you have any confusion related to this topic then feel free to ask in the comments section down below.

For a better understanding of this chapter, please check the detailed notes of the Electric charge and Fields. To watch Free Learning Videos on physics by Saransh Gupta sir Install the eSaral App.