Hey, do you want to know how to state the law of conservation of angular momentum? If so. Then you are at the right place.
It is a vector quantity, which is often represented by $\overrightarrow{\mathrm{L}}$ or $\overrightarrow{\mathrm{J}}$.
It is an axial vector (i.e. always perpendicular to the plane of motion)
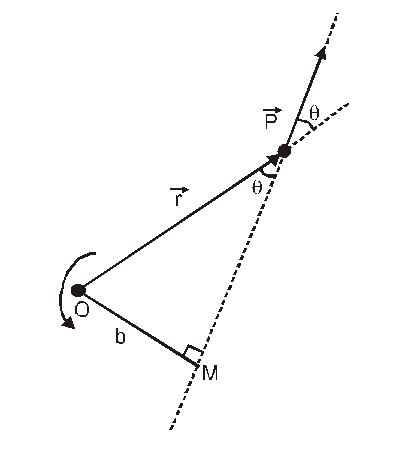
Angular momentum $\overrightarrow{\mathrm{J}}=\overrightarrow{\mathrm{r}} \times \overrightarrow{\mathrm{p}}$
$=\vec{r} \times(m \vec{v})$
$=m(\vec{r} \times \vec{v})$
Or $\overrightarrow{\mathrm{J}}=r p \sin \theta \hat{n}$
$\theta$ is angle between $\vec{r}$ and $\vec{v}$
$\hat{n}$ is unit vector perpendicular to plane of $\vec{r}$ and $\vec{v}$
The direction of angular momentum is perpendicular to the plane of $\overrightarrow{\mathrm{r}}$ and $\overrightarrow{\mathrm{v}}$ and it is given by right-hand screw rule.
If $\theta=0^{\circ}$
J = 0 (Minimum)
If $\theta=90^{\circ}$
J = m v r (Maximum)
S.I. Unit of J is Jule × sec (same as that of Planck’s const.)
Dimension: $\mathrm{M}^{1} \mathrm{~L}^{2} \mathrm{~T}^{-1}$
If direction of rotation is anticlockwise, angular momentum is taken positive and if direction of rotation is clockwise, angular momentum is taken negative.
The angular momentum of a system of particles is equal to the vector sum of angular momentum of each particle
$\overrightarrow{\mathrm{J}}=\overrightarrow{\mathrm{J}}_{1}+\overrightarrow{\mathrm{J}}_{2}+\overrightarrow{\mathrm{J}}_{3}+\ldots \ldots$
$\vec{J}=\sum_{i=1}^{n} \vec{J}_{i}$
$J=I \omega$
I - Moment of inertia with respect to axis of rotation
$\omega$ - Angular velocity due to angular momentum
J - The moment of momentum which is causing rotational motion.
The rate of change of angular momentum is equal to the torque applied on the body.
$\vec{\tau}=\frac{\mathrm{d} \overrightarrow{\mathrm{J}}}{\mathrm{dt}}$
In rotational motion angular momentum has equal importance as linear momentum in linear motion If torque acting of a particle is zero then
$\vec{\tau}=0 \Rightarrow \frac{\mathrm{d} \overrightarrow{\mathrm{J}}}{\mathrm{dt}}=0$
Or
$\overrightarrow{\mathrm{J}}=$ constant
Which implies that the angular momentum remains conserved when no external torque acts on the body.
$\overrightarrow{\mathrm{J}}=\overrightarrow{\mathrm{I} \omega}=$ constant
Proof : For a rigid body, rotating about a given axis.
$\vec{\tau}=\mathrm{I} \vec{\alpha}=\mathrm{I} \cdot \frac{\mathrm{d} \vec{\omega}}{\mathrm{dt}}$
Now, for a rigid body, rotating about a given axis, I remains constant.
Because
$\vec{\tau}=\mathrm{I} \cdot \frac{\mathrm{d} \vec{\omega}}{\mathrm{dt}}$
$=\frac{\mathrm{d}(\mathrm{I} \vec{\omega})}{\mathrm{dt}}=\frac{\mathrm{d} \overrightarrow{\mathrm{J}}}{\mathrm{dt}}$
If the external torque acting on the body, $\vec{\tau}=0$,
$\frac{\mathrm{d} \overrightarrow{\mathrm{J}}}{\mathrm{dt}}=0$
and hence $\vec{J}=$ constant.
For the equation $\mathrm{J}=\mathrm{I} \omega,$ it can be seen that if $\mathrm{J}$ remains constant, $\omega$ increases when I decreases and vice
versa. If I changed to $\mathrm{I}_{1}$, then, in the absence of an external torque, $\omega$ will change to $\omega_{1},$ such that
$\mathrm{I}_{\mathrm{i}} \omega_{\mathrm{i}}=\mathrm{I}_{\mathrm{f}} \omega_{\mathrm{f}}$
This is the law of conservation of angular momentum.
Example :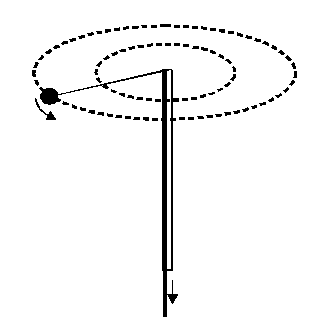
So, that's all from this article. If you get the idea about how to state the law of conservation of angular momentum then please share it with your friends.
For a better understanding of this chapter, please check the detailed notes of the Rotational Dynamics. To watch Free Learning Videos on physics by Saransh Gupta sir Install the eSaral App.
Angular momentum
The moment of linear momentum of a moving particle with respect to the axis of rotation is known as angular momentum.
It is a vector quantity, which is often represented by $\overrightarrow{\mathrm{L}}$ or $\overrightarrow{\mathrm{J}}$.
It is an axial vector (i.e. always perpendicular to the plane of motion)
Angular momentum $\overrightarrow{\mathrm{J}}=\overrightarrow{\mathrm{r}} \times \overrightarrow{\mathrm{p}}$
$=\vec{r} \times(m \vec{v})$
$=m(\vec{r} \times \vec{v})$
Or $\overrightarrow{\mathrm{J}}=r p \sin \theta \hat{n}$
$\theta$ is angle between $\vec{r}$ and $\vec{v}$
$\hat{n}$ is unit vector perpendicular to plane of $\vec{r}$ and $\vec{v}$
The direction of angular momentum is perpendicular to the plane of $\overrightarrow{\mathrm{r}}$ and $\overrightarrow{\mathrm{v}}$ and it is given by right-hand screw rule.
If $\theta=0^{\circ}$
J = 0 (Minimum)
If $\theta=90^{\circ}$
J = m v r (Maximum)
S.I. Unit of J is Jule × sec (same as that of Planck’s const.)
Dimension: $\mathrm{M}^{1} \mathrm{~L}^{2} \mathrm{~T}^{-1}$
If direction of rotation is anticlockwise, angular momentum is taken positive and if direction of rotation is clockwise, angular momentum is taken negative.
The angular momentum of a system of particles is equal to the vector sum of angular momentum of each particle
$\overrightarrow{\mathrm{J}}=\overrightarrow{\mathrm{J}}_{1}+\overrightarrow{\mathrm{J}}_{2}+\overrightarrow{\mathrm{J}}_{3}+\ldots \ldots$
$\vec{J}=\sum_{i=1}^{n} \vec{J}_{i}$
The relation between angular momentum and angular velocity
$J=I \omega$
I - Moment of inertia with respect to axis of rotation
$\omega$ - Angular velocity due to angular momentum
J - The moment of momentum which is causing rotational motion.
The rate of change of angular momentum is equal to the torque applied on the body.
$\vec{\tau}=\frac{\mathrm{d} \overrightarrow{\mathrm{J}}}{\mathrm{dt}}$
In rotational motion angular momentum has equal importance as linear momentum in linear motion If torque acting of a particle is zero then
$\vec{\tau}=0 \Rightarrow \frac{\mathrm{d} \overrightarrow{\mathrm{J}}}{\mathrm{dt}}=0$
Or
$\overrightarrow{\mathrm{J}}=$ constant
Which implies that the angular momentum remains conserved when no external torque acts on the body.
Law of Conservation of Angular Momentum
If no external torque is acting upon a body rotating about an axis, then the angular momentum of the body remains constant that is,$\overrightarrow{\mathrm{J}}=\overrightarrow{\mathrm{I} \omega}=$ constant
Proof : For a rigid body, rotating about a given axis.
$\vec{\tau}=\mathrm{I} \vec{\alpha}=\mathrm{I} \cdot \frac{\mathrm{d} \vec{\omega}}{\mathrm{dt}}$
Now, for a rigid body, rotating about a given axis, I remains constant.
Because
$\vec{\tau}=\mathrm{I} \cdot \frac{\mathrm{d} \vec{\omega}}{\mathrm{dt}}$
$=\frac{\mathrm{d}(\mathrm{I} \vec{\omega})}{\mathrm{dt}}=\frac{\mathrm{d} \overrightarrow{\mathrm{J}}}{\mathrm{dt}}$
If the external torque acting on the body, $\vec{\tau}=0$,
$\frac{\mathrm{d} \overrightarrow{\mathrm{J}}}{\mathrm{dt}}=0$
and hence $\vec{J}=$ constant.
For the equation $\mathrm{J}=\mathrm{I} \omega,$ it can be seen that if $\mathrm{J}$ remains constant, $\omega$ increases when I decreases and vice
versa. If I changed to $\mathrm{I}_{1}$, then, in the absence of an external torque, $\omega$ will change to $\omega_{1},$ such that
$\mathrm{I}_{\mathrm{i}} \omega_{\mathrm{i}}=\mathrm{I}_{\mathrm{f}} \omega_{\mathrm{f}}$
This is the law of conservation of angular momentum.
Example :
-
- A point mass is tied to one end of a cord whose other end passes through a vertical hollow tube, caught in one hand. The point mass is being rotated in a horizontal circle. The cord is then pulled down so that the radius of the circle reduces.Here the force on the point mass due to cord is radial and hence the torque about the center of rotation is zero therefore, the angular momentum must remain constant as the cord shortend.As cord is pulled down, the point mass rotates faster than before. The reason is that by shortening the radius of the circle, the moment of inertia of point mass about axis of rotation decreases
$\mathrm{I}_{\mathrm{i}} \omega_{\mathrm{i}}=\mathrm{I}_{\mathrm{f}} \omega_{\mathrm{f}}$
$\mathrm{I}_{\mathrm{i}}>\mathrm{I}_{\mathrm{f}}$
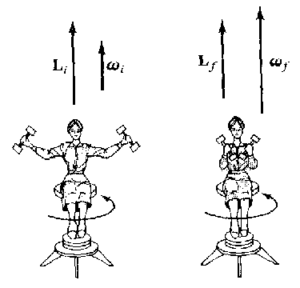
so $\omega_{i}<\omega_{f}$ - A man with his arms outstretched and holding heavy dumb bells in each hand, is standing at the centre of a rotating table. When the man pulls his arms, the speed of rotation of the table increases. The reason is that on pulling the arms, the distance R of the dumbells from the axis of rotation decreases and so the moment of inertia decreases. Therefore, by conservation of angular momentum, the angular velocity increases.
- When a diver jumps into water from a height, he does not keep his body straight but pulls in his arms and legs towards the centre of his body. On doing so, the moment of inertia I of his body decreases. But since the angular momentum I $\omega$ remains constant, his angular velocity $\omega$ correspondingly increases. Hence during jumping he can rotate his body in the air.
- In the same way, the ice skater and the ballet dancer increase or decrease the angular velocity of spin about a vertical axis by pulling or extending out their limbs.
- A : axis is horizontal ; angular momentum about vertical axis = 0.
B : axis is vertical ; angular momentum about vertical axis is still zero; man and chair spin in direction opposite to spin of the wheel.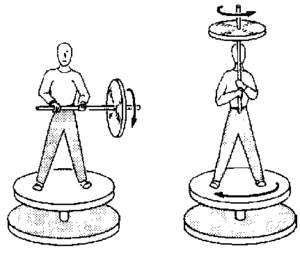
- The angular velocity of a planet around the Sun increases when it comes near the Sun. When a planet revolving around the Sun in an elliptical orbit comes near the Sun, the moment of inertia of the planet about the Sun decreases. In order to conserve angular momentum, the angular velocity shall increase. Similarly, when the planet is away from the Sun, there will be a decrease in the angular velocity.
- The speed of the inner layers of the whirlwind in a tornado is alarmingly high, In a tornado, the moment of inertia of air will go on decreasing as the air moves towards the center. This will be accompanied by an increase in angular velocity such that the angular momentum is conserved.
- A point mass is tied to one end of a cord whose other end passes through a vertical hollow tube, caught in one hand. The point mass is being rotated in a horizontal circle. The cord is then pulled down so that the radius of the circle reduces.Here the force on the point mass due to cord is radial and hence the torque about the center of rotation is zero therefore, the angular momentum must remain constant as the cord shortend.As cord is pulled down, the point mass rotates faster than before. The reason is that by shortening the radius of the circle, the moment of inertia of point mass about axis of rotation decreases
So, that's all from this article. If you get the idea about how to state the law of conservation of angular momentum then please share it with your friends.
For a better understanding of this chapter, please check the detailed notes of the Rotational Dynamics. To watch Free Learning Videos on physics by Saransh Gupta sir Install the eSaral App.