Hey, students do you want to know how to state the law of radioactive decay? If yes. Then read this article till the end.

Radioactive decay law

The rate of decay (number of disintegrations per second) is proportional to number of radioactive atoms (N) present at that time t

rate of decay $\frac{-\mathrm{d} \mathrm{N}}{\mathrm{dt}} \propto \mathrm{N}$

or $\frac{\mathrm{d} \mathrm{N}}{\mathrm{dt}}=-\lambda \mathrm{N}$

or $\quad N=N_{0} e^{-\lambda t}$…..(1)

where $\lambda$ is disintegration constant, $\mathrm{N}_{0}$ = number of active atoms at t = 0

1. Equation one is the radioactive decay law. It shows that the number of active nuclei decreases exponentially with time.
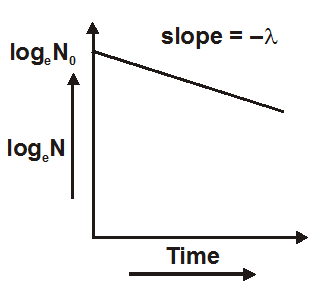
2. The fraction of active atoms remaining at time t is$\frac{\mathrm{N}}{\mathrm{N}_{0}}=\mathrm{e}^{-\lambda \mathrm{t}}$
3. The number of atoms that have decayed in time t is$N_{0}-N$
   
   $=N_{0}\left(1-e^{-\lambda t}\right)$
4. The fraction of atoms that have decayed in time t is$\frac{N_{0}-N}{N_{0}}$
   
   $=1-e^{-\lambda t}$
   

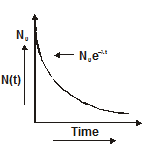
Decay constant

1. Decay constant$\lambda=\frac{-\mathrm{d} \mathrm{N} / \mathrm{dt}}{\mathrm{N}}$
   
   $=\frac{\text { rate of decay }}{\text { number of active atoms }}$



2. at $t=\frac{1}{\lambda}$$\mathrm{N}=\frac{\mathrm{N}_{0}}{\mathrm{e}}$
   
   The decay constant of a radioactive element is equal to the reciprocal of the time after which the number of remaining active atoms reduces to $\frac{1}{\mathrm{e}}$ times of original value.



3. at $t=\frac{1}{\lambda}$fraction of active nuclei left
   
   $\frac{\mathrm{N}}{\mathrm{N}_{0}}=\frac{1}{\mathrm{e}}=0.37$
   
   or $37 \%$
   
   fraction of decayed nuclei
   
   $1-\frac{N}{N_{0}}$
   
   $=0.63=63 \%$
4. $\lambda=\frac{\mathrm{dN} / \mathrm{N}}{\mathrm{dt}}$ The decay constant is the probability of decay per active atom per unit time.



5. The decay constant depends on the nature of the radioactive substance and is independent of temperature, pressure, force, etc.



6. The decay constant for a stable substance is zero



7. Unit of decay constant is second $^{-1}$ and dimension is $\mathrm{T}^{-1}$



8. If there are more than one radioactive elements in a group then the resultant decay constant is equal to sum of individual decay constants
   
   $\lambda=\lambda_{1}+\lambda_{2}+\lambda_{3}+$……..
   
   or
   
   $\frac{1}{\mathrm{~T}}=\frac{1}{\mathrm{~T}_{1}}+\frac{1}{\mathrm{~T}_{2}}+\ldots$

Half life

The time in which the number of radioactive atoms reduce to half of its initial value is known as half-life i.e. at

$\mathrm{t}=\mathrm{T}$

$N=\frac{N_{0}}{2}$

from radioactive decay law

$\frac{N_{0}}{2}=N_{0} e^{-\lambda T}$

or

$\mathrm{T}=\frac{0.693}{\lambda}$

1. The half-life depends on the nature of radioactive elements.
2. The half-life of an element indicates the rate of decay. When half-life is a large rate of decay is small.
3. After t = nT number of active atoms left$N=\frac{N_{0}}{2^{n}}$
   
   $=\frac{1}{2^{t / T}} \cdot \mathrm{N}_{0}$
   
   where T = half-life and n = number of half-lives.
4. Number of radioactive atoms decayed in n half-lives$N_{0}-\frac{N_{0}}{2^{n}}$
   $=N_{0}\left(\frac{2^{n}-1}{2^{n}}\right)$
5. The half-life for a given radioactive substance is constant. It does not change with time. It is unaffected by pressure, temperature, etc.

so, that’s all from this blog, I hope you get the idea about how to state the law of radioactive decay. If you found this article informative then please share it with your friends.

Also, read
Uses Of radioactive Isotopes 

To watch Free Learning Videos on physics by Saransh Gupta sir Install the eSaral App.