JEE Main Previous Year Question of Math with Solutions are available at eSaral. Practicing JEE Main Previous Year Papers Questions of mathematics will help the JEE aspirants in realizing the question pattern as well as help in analyzing weak & strong areas.
eSaral helps the students in clearing and understanding each topic in a better way. eSaral is providing complete chapter-wise notes of Class 11th and 12th both for all subjects.
Besides this, eSaral also offers NCERT Solutions, Previous year questions for JEE Main and Advance, Practice questions, Test Series for JEE Main, JEE Advanced and NEET, Important questions of Physics, Chemistry, Math, and Biology and many more.
Download eSaral app for free study material and video tutorials.
Q. If the mean deviation of the numbers 1, 1 + d, 1 + 2d, ..., 1 + 100d from their mean is 255, then that d is equal to-
(1) 10.1 (2) 20.2 (3) 10.0 (4) 20.0
[AIEEE-2009]
Ans. (1)
Q M.D. of A.P. a, a $+\mathrm{d}, \mathrm{a}+2 \mathrm{d}, \ldots . \mathrm{a}+2 \mathrm{nd}$
about mean is M.D.: $=\frac{\mathrm{n}(\mathrm{n}+1)}{2 \mathrm{n}+1} \mathrm{ld}$
given numbers $1,1+\mathrm{d}, 1+2 \mathrm{d}, \ldots 1+100 \mathrm{d}$ are in A.P. and its M.D. is $255 .$
Here $\mathrm{a}=1,2 \mathrm{nd}=100 \mathrm{d}$ i.e. $\mathrm{n}=50$
$\therefore \quad \frac{50 \times 51}{101}|\mathrm{d}|=255 \quad \Rightarrow \quad \mathrm{d}=10.1$
Q. Statement-1: The variance of first n even natural numbers is $\frac{\mathrm{n}^{2}-1}{4}$
Statement-2 : The sum of first n natural numbers is $\frac{\mathrm{n}(\mathrm{n}+1)}{2}$ and the sum of squares of first n natural numbers is $\frac{\mathrm{n}(\mathrm{n}+1)(2 \mathrm{n}+1)}{6}$
(1) Statement–1 is true, Statement–2 is false.
(2) Statement–1 is false, Statement–2 is true.
(3) Statement–1 is true, Statement–2 is true ; Statement–2 is a correct explanation for Statement–1.
(4) Statement–1 is true, Statement–2 is true ; Statement–2 is not a correct explanation for statement–1.
[AIEEE-2009]
Ans. (2)
Sum of first n even natural numbers
$\Sigma \mathrm{x}_{\mathrm{i}}=2+4+6+\ldots \ldots+2 \mathrm{n}$
$=2[1+2+3+\ldots+\mathrm{n}]=\mathrm{n}(\mathrm{n}+1)$
Sum of square of first n even natural numbers
$\Sigma \mathrm{x}_{\mathrm{i}}^{2}=2^{2}+4^{2}+6^{2}+\ldots \ldots+(2 \mathrm{n})^{2}$
$=2^{2}\left[1^{2}+2^{2}+3^{2}+\ldots+\mathrm{n}^{2}\right]=\frac{2 \mathrm{n}(\mathrm{n}+1)(2 \mathrm{n}+1)}{3}$
Variance of first n even natural numbers
$\sigma^{2}=\frac{\Sigma x_{i}^{2}}{n}-\left(\frac{\Sigma x_{i}}{n}\right)^{2}$
$=\frac{2(n+1)(2 n+1)}{3}-(n+1)^{2}=\frac{n^{2}-1}{3}$
So, statement- 1 is false and statement- 2 is true.
Q. For two data sets each of size is 5, the variances are given to be 4 and 5 and the corresponding means are given to be 2 and 4 respectively, then the variance of the combined data set is :-
(1) $\frac{5}{2}$ (2) $\frac{11}{2}$ (3) 6 (4) $\frac{13}{2}$
[AIEEE-2010]
Ans. (2)
Here $n_{1}=n_{2}=5, \sigma_{1}^{2}=4, \sigma_{2}^{2}=5, \bar{x}_{1}=2, \bar{x}_{2}=4$
Variance of combined set
$\sigma^{2}=\frac{n_{1} \sigma_{1}^{2}+n_{2} \sigma_{2}^{2}}{n_{1}+n_{2}}+\frac{n_{1} n_{2}}{\left(n_{1}+n_{2}\right)^{2}}\left(\bar{x}_{1}-\bar{x}_{2}\right)^{2}$
$=\frac{5 \times 4+5 \times 5}{(5+5)}+\frac{5 \times 5}{(5+5)^{2}}(2-4)^{2}=\frac{9}{2}+1=\frac{11}{2}$
Q. If the mean deviation about the median of the numbers a, $2 a, \ldots \ldots ., 50 \mathrm{a}$ is $50,$ then $|\mathrm{a}|$ equals:
(1) 4 (2) 5 (3) 2 (4) 3
[AIEEE-2011]
Ans. (1)
Mediam $=25.5 \mathrm{a}$
$\begin{aligned} \mathrm{x}_{\mathrm{i}}: & \mathrm{a} \\\left|\mathrm{x}_{\mathrm{i}}-\mathrm{M}\right|: & \mathrm{a} 4.5 \mathrm{a} \quad 2 \mathrm{a} \quad 3 \mathrm{a} \ldots \ldots \ldots \ldots 50 \mathrm{a} \\\left|\mathrm{x}_{\mathrm{i}}-\mathrm{M}\right|: & 24.5 \mathrm{a} \quad 23.5 \mathrm{a} \quad \ldots \ldots \ldots \ldots .24 .5 \mathrm{a} \\ \sum\left|\mathrm{x}_{\mathrm{i}}-\mathrm{M}\right| &=[24.5 \mathrm{a}+23.5 \mathrm{a}+\ldots \ldots+0.5 \mathrm{a}+0.5 \mathrm{a}+\ldots \ldots+24.5 \mathrm{a}] \\ &=2 \mathrm{a}[0.5+1.5+\ldots \ldots+24.5] \\ &=2 \mathrm{a}[0.5+1.5+\ldots \ldots+24.5] \\ \sum_{\mathrm{i}}\left|\mathrm{x}_{\mathrm{i}}-\mathrm{M}\right| &=25 \times 25 \mathrm{a} \\ 50 &=\frac{25 \times 25 \mathrm{a}}{50} \Rightarrow \mathrm{a}=4 \end{aligned}$
Q. A scientist is weighing each of 30 fishes. Their mean weight worked out is 30 gm and a standard deviation of 2 gm. Later, it was found that the measuring scale was misaligned and always under reported every fish weight by 2 gm. The correct mean and standard deviation (in gm) of fishes are respectively :
(1) 28, 4 (2) 32, 2 (3) 32, 4 (4) 28, 2
[AIEEE-2011]
Ans. (2)
$\overline{\mathrm{x}}=$ mean $=\frac{\Sigma \mathrm{x}_{\mathrm{i}}}{\mathrm{n}}$
mean of $\mathrm{x}_{\mathrm{i}}$ is given as $30 \mathrm{gm}$
If each data is increased by some number
(i.e. $2)$ the mean is also increased by $2 .$
i.e. corrected mean $=30+2=32 \mathrm{gm}$
$\sigma=$ standard deviation $=\sqrt{\frac{\Sigma\left|\mathrm{x}_{\mathrm{r}_{1}}-\overline{\mathrm{x}}\right|^{2}}{\mathrm{n}}}$
standard deviation does not depend on change of origin so if every data is increased by same number (i.e. 2) then standard deviation remains same.
So the corrected standard deviation = 2gm.
Q. Let $\mathrm{x}_{1}, \mathrm{x}_{2}, \ldots, \mathrm{x}_{\mathrm{n}}$ be n observations, and let $\overline{\mathrm{x}}$ be their arithmetic mean and $\sigma^{2}$ be their variance.
Statement-1: Variance of $2 \mathrm{x}_{1}, 2 \mathrm{x}_{2}, \ldots, 2 \mathrm{x}_{\mathrm{n}}$ is $4 \sigma^{2}$
Statement-2 : Arithmetic mean of $2 \mathrm{x}_{1}, 2 \mathrm{x}_{2}, \ldots, 2 \mathrm{x}_{\mathrm{n}}$ is $4 \overline{\mathrm{x}}$.
(1) Statement–1 is true, Statement–2 is false.
(2) Statement–1 is false, Statement–2 is true.
(3) Statement–1 is true, Statement–2 is true ; Statement–2 is a correct explanation for Statement–1.
(4) Statement–1 is true, Statement–2 is true ; Statement–2 is not a correct explanation for Statement–1.
[AIEEE-2012]
Ans. (1)
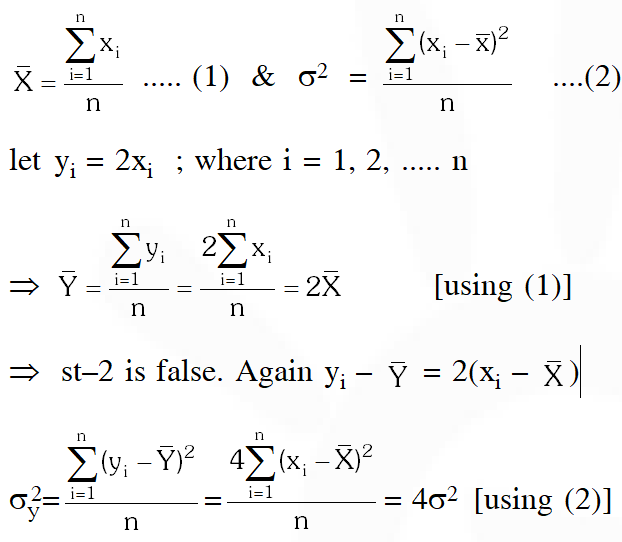therefore st–1 is true
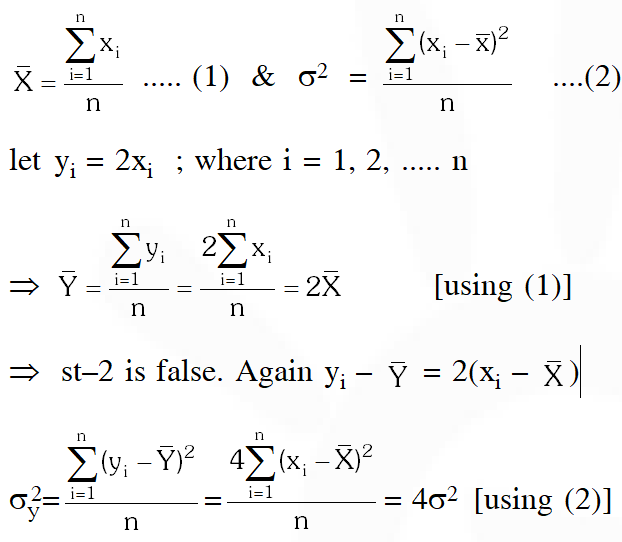therefore st–1 is true
Q. All the students of a class performed poorly in Mathematics. The teacher decided to give grace marks of 10 to each of the students. Which of the following statistical measures will not change even after the grace marks were given?
(1) mean (2) median (3) mode (4) variance
[JEE-MAINS-2013]
Ans. (4)
Variance is independent of change of origin.
Q. The variance of first 50 even natural numbers is:-
(1) $\frac{833}{4}$ (2) 833 (3) 437 (4) $\frac{437}{4}$
[JEE(Main)-2014]
Ans. (2)
We have to calculate variance of the data
2, 4, 6, 8, ....., 100
$\sigma^{2}=\frac{\sum \mathrm{x}_{\mathrm{i}}^{2}}{\mathrm{n}}-\left(\frac{\sum \mathrm{x}_{\mathrm{i}}}{\mathrm{n}}\right)^{2}$
Now, $\sum x_{i}^{2}=2^{2}+4^{2}+\ldots+100^{2}=\frac{4.50 .51 .101}{6}$
Now, $\quad \frac{\sum x_{i}^{2}}{50}=3434$
Also, $\left(\frac{\sum x_{i}}{n}\right)^{2}=\left(\frac{2.50 .51}{2.50}\right)^{2}=2601$
$\therefore \sigma^{2}=3434-2601=833$.
Q. The mean of the data set comprising of 16 observations is 16. If one of the observation valued 16 is deleted and three new observations valued 3, 4 and 5 are added to the data, then the mean of the resultant data, is :
(1) 15.8 (2) 14.0 (3) 16.8 (4) 16.0
[JEE(Main)-2015]
Ans. (2)
$\Sigma \mathrm{x}_{\mathrm{i}}=256$
Let new observations $\mathrm{X}_{\mathrm{i}}$
$\Sigma \mathrm{X}_{\mathrm{i}}=(256-16)+(3+4+5)=252$
$\&$ number of observations 18
$\therefore$ New mean $=\frac{\Sigma \mathrm{X}_{\mathrm{i}}}{18}=14$
Q. If the standard deviation of the numbers 2, 3, a and 11 is 3.5, then which of the following is true ?
(1) $3 a^{2}-23 a+44=0$
(2) $3 \mathrm{a}^{2}-26 \mathrm{a}+55=0$
(3) $3 a^{2}-32 a+84=0$
(4) $3 a^{2}-34 a+91=0$
[JEE(Main)-2016]
Ans. (3)
$\because \mathrm{S.D.}=\sqrt{\frac{\Sigma \mathrm{x}_{\mathrm{i}}^{2}}{\mathrm{n}}-\left(\frac{\Sigma \mathrm{x}_{\mathrm{i}}}{\mathrm{n}}\right)^{2}}$
$\therefore \frac{49}{4}=\frac{4+9+\mathrm{a}^{2}+121}{4}-\left(\frac{16+\mathrm{a}}{4}\right)^{2}$
$\Rightarrow 3 \mathrm{a}^{2}-32 \mathrm{a}+84=0$
Q. If $\sum_{i=1}^{9}\left(x_{i}-5\right)=9$ and $\sum_{i=1}^{9}\left(x_{i}-5\right)^{2}=45,$ then the standard deviation of the 9 items $x_{1}, x_{2}, \ldots ., x_{9}$ is
(1) 4 (2) 2 (3) 3 (4) 9
[JEE(Main)-2018]
Ans. (2)
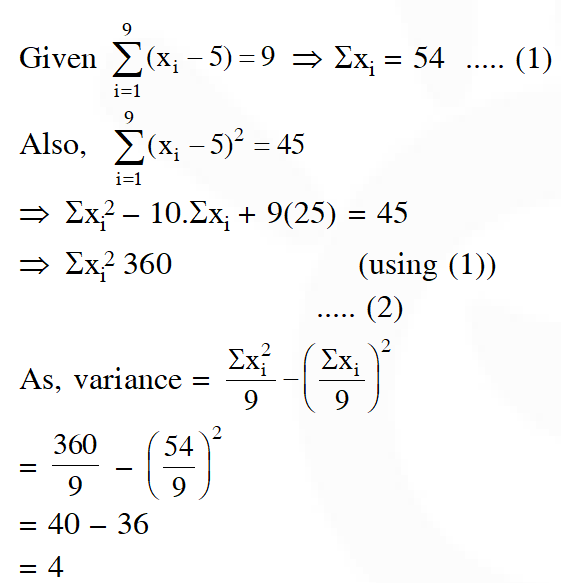Hence standard deviation is 2 (As standared deviation $=\sqrt{\text { var iance }}$
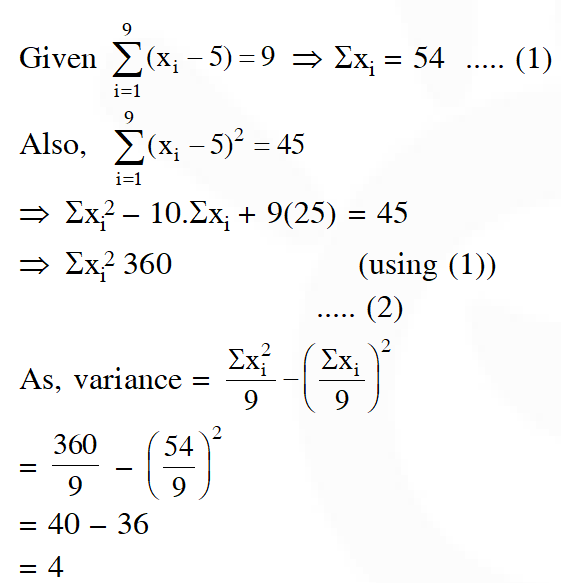Hence standard deviation is 2 (As standared deviation $=\sqrt{\text { var iance }}$
Q. The mean of a set of 30 observations is 75. If each observation is multiplied by a non-zero number $\lambda$ and then each of them is decreased by 25, their mean remains the same. Then $\lambda$ is equal to
(1) $\frac{2}{3}$ (2) $\frac{10}{3}$ (3) $\frac{1}{3}$ ( 4)$\frac{4}{3}$
[JEE(Main)-2018]
Ans. (4)
Q. If the mean of the data $: 7,8,9,7,8,7, \lambda, 8$ is $8,$ then the variance of this data is :-
(1) 2 (2) $\frac{7}{8}$ (3) $\frac{9}{8}$ (4) 1
[JEE(Main)-2018]
Ans. (4)
Q. The mean and the standard deviation(s.d.) of five observations are 9 and 0, respectively. If one of the observations is changed such that the mean of the new set of five observations becomes 10, then their s.d. is :
(1) 0 (2) 1 (3) 4 (4) 2
[JEE(Main)-2018]
Ans. (4)