Tangent galvanometer is an early measuring instrument for small electric currents. It consists of a coil of insulated copper wire wound on a circular non-magnetic frame. Its working is based on the principle of the tangent law of magnetism. When a current is passed through the circular coil, a magnetic field (B) is produced at the center of the coil in a direction perpendicular to the plane of the coil. Here we will study about the Tangent Law and Tangent Galvanometer Experiment with Construction & Working.
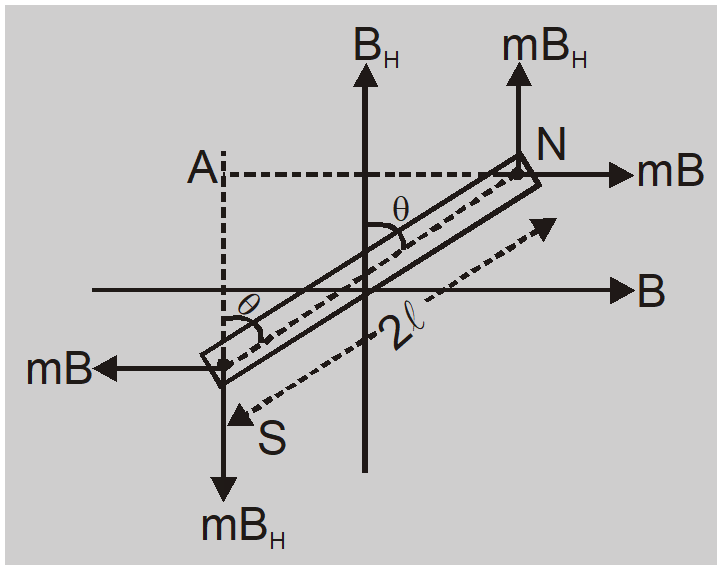When a bar magnet is kept in two mutually perpendicular magnetic fields then each field will exert a couple on the magnet tending to set it parallel to itself. The torque due to $B_{H}$ ries to rotate the magnet in anticlockwise direction while torque due to B in clockwise direction.
In equilibrium torque due to $B_{H}=$ torque due to B
$mB _{ H } \times AN = mB \times AS$ so $B = B _{ H } \frac{ AN }{ AS }= B _{ H } \tan \theta$
Ex. Two tangent galvanometers differ only in the matter of number of turns in the coil. On passing current through the two joined in series, the first shows a deflection of $35^{\circ}$ and the other shows a $45^{\circ}$ deflection. Calculate the ratio of their number of turns. Use tan $35^{\circ}=0.7$ Sol. In tangent galvanometer $\frac{\mu_{0} NI }{2 r }= B _{ H } \tan \theta$ Here $N \propto \tan \theta$ so $\frac{N_{1}}{N_{2}}=\frac{\tan \theta_{1}}{\tan \theta_{2}}=\frac{\tan 35}{\tan 45}=\tan 35=\frac{7}{10}$ Required ratio is 7 : 10
Ex. Two tangent galvanometers A and B have their number of turns in the ratio 1 : 3 and diameters in the ratio 1 : 2 (a) which galvanometer has greater reduction factor (b) which galvanometer shows greater deflection when both are connected in series to a dc source? Sol. (a) $K =\frac{2 a }{ n \mu_{0}} B _{ H }$ so $\frac{ K _{1}}{ K _{2}}=\frac{ a _{1}}{ a _{2}} \cdot \frac{ n _{2}}{ n _{1}}=3 \times \frac{1}{2}=\frac{3}{2}$ or $K _{1}=\frac{3}{2} K _{2}$ so $K _{1}> K _{2}$ Galvanometer A has greater reduction factor (b) $\frac{\mu_{0} nI }{2 a }= B _{ H } \tan \theta$ so $\tan \theta \propto \frac{n}{a}$ $\frac{\tan \theta_{1}}{\tan \theta_{2}}=\frac{n_{1}}{a_{1}} \times \frac{a_{2}}{n_{2}}=\frac{1}{3} \times \frac{2}{1}=\frac{2}{3}$ so $\tan \theta_{1}>\tan \theta_{2}$ or $\theta_{2}>\theta_{1}$ so B shows greater deflection.
Also Read: Biot Savart's Law Click here for the Video tutorials of Magnetic Effect of Current Class 12
Tangent Law
If a small bar magnet is suspended in two mutually perpendicular uniform magnetic fields B and $B_{H}$ such that it comes to rest making angle $\theta$ with direction of field $B _{ H }$ then $B = B _{ H }$ tan $\theta$
When a bar magnet is kept in two mutually perpendicular magnetic fields then each field will exert a couple on the magnet tending to set it parallel to itself. The torque due to $B_{H}$ ries to rotate the magnet in anticlockwise direction while torque due to B in clockwise direction.
In equilibrium torque due to $B_{H}=$ torque due to B
$mB _{ H } \times AN = mB \times AS$ so $B = B _{ H } \frac{ AN }{ AS }= B _{ H } \tan \theta$
Tangent Galvanometer
It is an instrument used to measure very small currents. It is a galvanometer with a fixed coil and moving magnet. It is based on tangents law.Construction & Working
It consists of a circular coil of a large number of turns of insulated copper wire wound on vertical circular frame of non magnetic material. This frame can be rotated about its vertical diameter as axis. A small magnetic compass needle pivoted at centre is free to rotate in horizontal plane over a horizontal circular scale graduated in degrees. The position of needle is read by a long aluminium pointer attached at right angles to magnetic needle. Initially coil is made vertical by levelling screws and coil is brought in magnetic meridian. Now $B_{H}$ is in plane of coil. As current is passed through coil magnetic field B is produced which is perpendicular to plane of coil. According to Tangent law $B=B_{H} \tan \theta$ or $\frac{\mu_{0} nI }{2 a }= B _{ H } \tan \theta$ Or $I =\frac{2 a }{ n \mu_{0}} B _{ H } \tan \theta=\frac{ B _{ H }}{ G _{1}} \tan \theta= K \tan \theta$ where $G _{1}=\frac{ n \mu_{0}}{2 a }$ is galvanometer constant and $K =\frac{ B _{ H }}{ G _{1}}$ $K =\frac{ B _{ H }}{ G _{1}}$ If $\theta=45^{\circ}$ then = K, so reduction factor of a tangent galvanometer is numerically equal to the current in ampere through the galvanometer which produces a deflection of $45^{\circ}$ when the plane of its coil lies in the magnetic meridian. K depends on geometry of coil and value of $B_{H}$.Sensitivity
A tangent galvanometer is both sensitive and accurate if the change in its deflection is large for a given fractional change in current. $I=K \tan \theta \quad$ or $dI = K \sec ^{2} \theta d \theta$ or $\frac{ d I }{ I }=\frac{ d \theta}{\sin \theta \cos \theta}=\frac{2 d \theta}{\sin 2 \theta} \quad$ or $\quad d \theta=\frac{\sin 2 \theta}{2} \frac{ d I }{ I }$ $d \theta=( d \theta)_{\max }$ if $\sin 2 \theta=1=\sin \frac{\pi}{2}$ $SO$ $\theta=\frac{\pi}{4}$ The tangent galvanometer has maximum sensitivity when $\theta=45^{\circ}$.Ex. Two tangent galvanometers differ only in the matter of number of turns in the coil. On passing current through the two joined in series, the first shows a deflection of $35^{\circ}$ and the other shows a $45^{\circ}$ deflection. Calculate the ratio of their number of turns. Use tan $35^{\circ}=0.7$ Sol. In tangent galvanometer $\frac{\mu_{0} NI }{2 r }= B _{ H } \tan \theta$ Here $N \propto \tan \theta$ so $\frac{N_{1}}{N_{2}}=\frac{\tan \theta_{1}}{\tan \theta_{2}}=\frac{\tan 35}{\tan 45}=\tan 35=\frac{7}{10}$ Required ratio is 7 : 10
Ex. Two tangent galvanometers A and B have their number of turns in the ratio 1 : 3 and diameters in the ratio 1 : 2 (a) which galvanometer has greater reduction factor (b) which galvanometer shows greater deflection when both are connected in series to a dc source? Sol. (a) $K =\frac{2 a }{ n \mu_{0}} B _{ H }$ so $\frac{ K _{1}}{ K _{2}}=\frac{ a _{1}}{ a _{2}} \cdot \frac{ n _{2}}{ n _{1}}=3 \times \frac{1}{2}=\frac{3}{2}$ or $K _{1}=\frac{3}{2} K _{2}$ so $K _{1}> K _{2}$ Galvanometer A has greater reduction factor (b) $\frac{\mu_{0} nI }{2 a }= B _{ H } \tan \theta$ so $\tan \theta \propto \frac{n}{a}$ $\frac{\tan \theta_{1}}{\tan \theta_{2}}=\frac{n_{1}}{a_{1}} \times \frac{a_{2}}{n_{2}}=\frac{1}{3} \times \frac{2}{1}=\frac{2}{3}$ so $\tan \theta_{1}>\tan \theta_{2}$ or $\theta_{2}>\theta_{1}$ so B shows greater deflection.
Also Read: Biot Savart's Law Click here for the Video tutorials of Magnetic Effect of Current Class 12
About eSaral At eSaral we are offering a complete platform for IIT-JEE & NEET preparation. The main mission behind eSaral is to provide education to each and every student in India by eliminating the Geographic and Economic factors, as a nation’s progress and development depends on the availability of quality education to each and every one. With the blend of education & technology, eSaral team made the learning personalized & adaptive for everyone.For free video lectures and complete study material, Download eSaral APP.