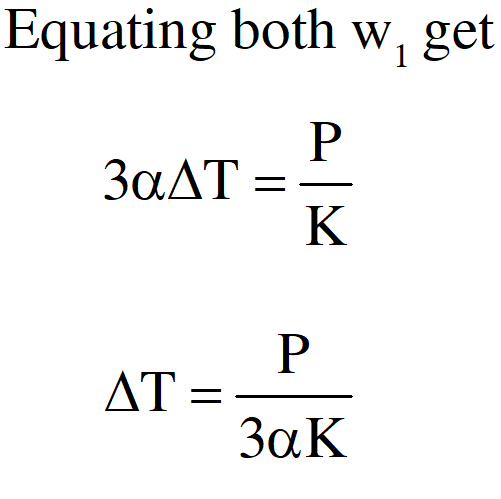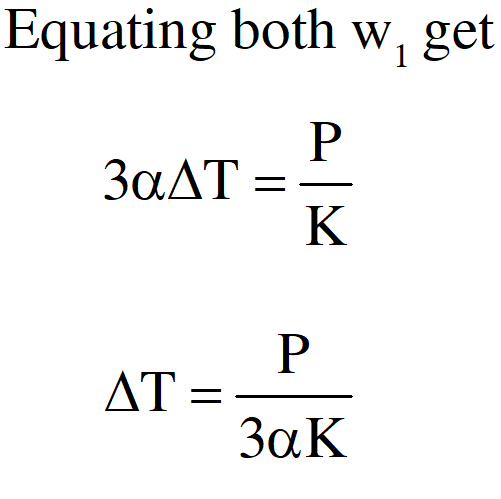JEE Main Previous Year Question of Physics with Solutions are available here. Practicing JEE Main Previous Year Papers Questions of Physics will help all the JEE aspirants in realizing the question pattern as well as help in analyzing their weak & strong areas.
Get detailed Class 11th &12th Physics Notes to prepare for Boards as well as competitive exams like IIT JEE, NEET etc.
eSaral helps the students in clearing and understanding each topic in a better way. eSaral is providing complete chapter-wise notes of Class 11th and 12th both for all subjects.
Besides this, eSaral also offers NCERT Solutions, Previous year questions for JEE Main and Advance, Practice questions, Test Series for JEE Main, JEE Advanced and NEET, Important questions of Physics, Chemistry, Math, and Biology and many more.
Download eSaral app for free study material and video tutorials.
Q. Two wires are made of the same material and have the same volume. However wire 1 has cross-sectional area A and wire 2 has cross-sectional area 3A. If the length of wire 1 increases by Dx on applying force F, how much force is needed to stretch wire 2 by the same amount ?
(1) 6F (2) 9F (3) F (4) 4F
[AIEEE-2009]
Ans. (2)
. $\mathrm{A} \ell_{1}=3 \mathrm{A} \ell_{2}$
$\Rightarrow \ell_{2}=\frac{\ell_{1}}{3}$
For wire $1: Y=\frac{F / A}{\Delta x / \ell_{1}}$
For wire $2: \mathrm{Y}=\frac{F^{\prime} / 3 A}{\Delta x / \ell_{2}}$
$\Rightarrow \mathrm{F}^{\prime}=9 \mathrm{F}$
Q. A wooden wheel of radius R is made of two semicircular parts (see figure). The two parts are held together by a ring made of a metal strip of cross sectional area S and Length L. L is slightly less than $2 \pi \mathrm{R}$. To fit the ring on the wheel, it is heated so that its temperature rises by $\Delta \mathrm{T}$ and it just steps over the wheel. As it cools down to surrounding temperature, it presses the semicircular parts together. If the coefficient of linear expansion of the metal is , and its Young's modulus is Y, the force that one part of the wheel applies on the other part is :
 [AIEEE 2012]
[AIEEE 2012]
 [AIEEE 2012]
[AIEEE 2012]
Ans. (1)
$Y=\frac{F / S}{\Delta L / L}$
$\frac{\Delta L}{L}=\frac{\Delta R}{R}=\alpha \Delta \mathrm{T} \quad[\mathrm{L}=2 \pi \mathrm{R}]$
$\Rightarrow \mathrm{F}=\mathrm{YS} \alpha \Delta \mathrm{T}$
$\therefore$ The ring is pressing the wheel
from both sides, thus
$\mathrm{F}_{\mathrm{net}}=2 \mathrm{F}=2 \mathrm{YS} \alpha \Delta \mathrm{T}$
Q. The pressure that has to be applied to the ends of a steel wire of length 10 cm to keep its length constant when its temperature is raised by $100^{\circ} \mathrm{C}$ is :
(For steel Young's modulus is $2 \times 10^{11} \mathrm{Nm}^{-2}$ and coefficient of thermal expansion is $1.1 \times 10^{-5} \mathrm{K}^{-1}$ )
(1) $2.2 \times 10^{7} \mathrm{Pa}$
(2) $2.2 \times 10^{6} \mathrm{Pa}$
(3) $2.2 \times 10^{8} \mathrm{Pa}$
(4) $2.2 \times 10^{9} \mathrm{Pa}$
[JEE-Main-2014]
Ans. (3)
Thermal strain $=\alpha \Delta \mathrm{T}$
(by $\left.\ell=\ell_{0}(1+\alpha \Delta \mathrm{T})\right)$
$\Rightarrow$ Thermal stress in Rod (Pressure due to
Thermal strain $)=\mathrm{Y} \alpha \Delta \mathrm{T}$
$=2 \times 10^{11} \times 1.1 \times 10^{-5} \times 100$
$=2.2 \times 10^{8} \mathrm{Pa}$
Q. A pendulum made of a uniform wire of cross sectional area A has time period T. When an additional mass M is added to its bob, the time period changes to $\mathrm{T}_{\mathrm{M}}$. If the Young's modulus of the material of the wire is Y then $\frac{1}{\mathrm{Y}}$ is equal to :- (g = gravitational acceleration)
( 1)$\left[1-\left(\frac{\mathrm{T}_{\mathrm{M}}}{\mathrm{T}}\right)^{2}\right] \frac{\mathrm{A}}{\mathrm{Mg}}$
( 2)$\left[1-\left(\frac{\mathrm{T}}{\mathrm{T}_{\mathrm{M}}}\right)^{2}\right] \frac{\mathrm{A}}{\mathrm{Mg}}$
( 3)$\left[\left(\frac{\mathrm{T}_{\mathrm{M}}}{\mathrm{T}}\right)^{2}-1\right] \frac{\mathrm{A}}{\mathrm{Mg}}$
( 4)$\left[\left(\frac{\mathrm{T}_{\mathrm{M}}}{\mathrm{T}}\right)^{2}-1\right] \frac{\mathrm{Mg}}{\mathrm{A}}$
[JEE-Main-2015]
Ans. (3)
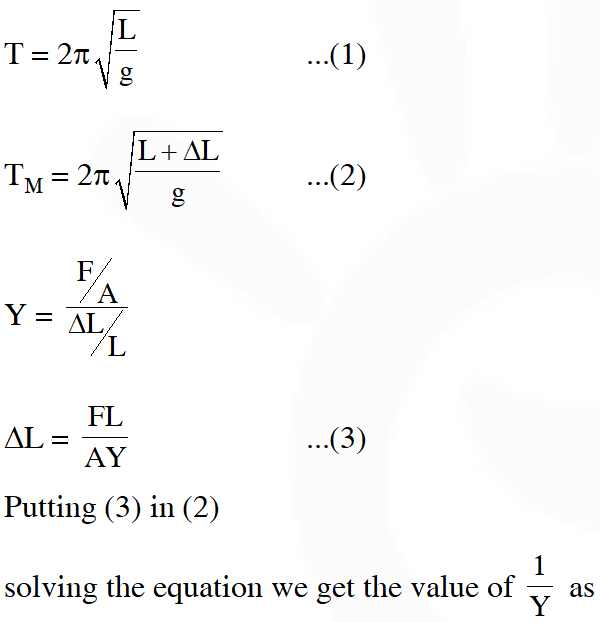
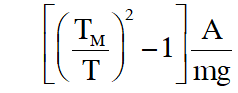
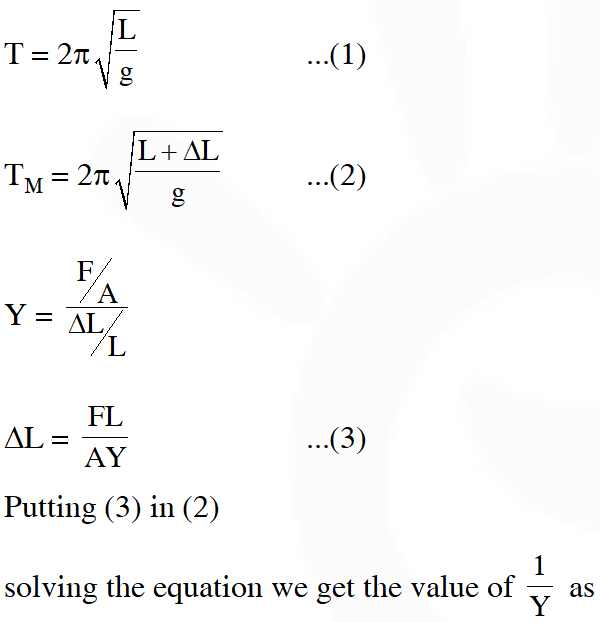
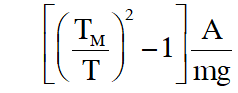
Q. A pendulume clock loses 12s a day if the temperature is $40^{\circ} \mathrm{C}$ and gains 4s a day if the temperature is $20^{\circ} \mathrm{C}$. The temperature at which the clock will show correct time, and the coeffecient of linear expansion $(\alpha)$ of the metal of the pendulum shaft are respectively :-
(1) $55^{\circ} \mathrm{C} ; \alpha=1.85 \times 10^{-2} /^{\circ} \mathrm{C}$
(2) $25^{\circ} \mathrm{C} ; \alpha=1.85 \times 10^{-5} /^{\circ} \mathrm{C}$
(3) $60^{\circ} \mathrm{C} ; \alpha=1.85 \times 10^{-4} /^{\circ} \mathrm{C}$
(4) $30^{\circ} \mathrm{C} ; \alpha=1.85 \times 10^{-3} /^{\circ} \mathrm{C}$
[JEE-Main-2016]
Ans. (2)
$\mathrm{T}=2 \pi \sqrt{\frac{\ell}{\mathrm{g}}}$
$\frac{\Delta \mathrm{T}}{\mathrm{T}}=\frac{1}{2} \frac{\Delta \ell}{\ell}$
When clock gain 12 sec
$\frac{12}{\mathrm{T}}=\frac{1}{2} \alpha(40-\theta)$ …. (1)
When clock lose 4 sec.
$\frac{4}{\mathrm{T}}=\frac{1}{2} \alpha(\theta-20) \quad \ldots(2)$
From equation (1) & (2)
$3=\frac{40-\theta}{\theta-20}$
$3 \theta-60=40-\theta$
$4 \theta=100$
$\theta=25^{\circ} \mathrm{C}$
from equation (1)
$\frac{12}{\mathrm{T}}=\frac{1}{2} \alpha(40-25)$
$\frac{12}{24 \times 3600}=\frac{1}{2} \alpha \times 15$
$\alpha=\frac{24}{24 \times 3600 \times 15}$
$\alpha=1.85 \times 10^{-15} /^{\circ} \mathrm{C}$
Q. An external pressure P is applied on a cube at $0^{\circ} \mathrm{C}$ so that it is equally compressed from all sides. K is the bulk modulus of the material of the cube and $\alpha$ is its coefficient of linear expansion. Suppose we want to bring the cube to its original size by heating. The temperature should be raised by :
(1) $\frac{3 \alpha}{\mathrm{PK}}$
(2) $3 \mathrm{PK} \alpha$
(3) $\frac{\mathrm{P}}{3 \alpha \mathrm{K}}$
(4) $\frac{\mathrm{P}}{\alpha \mathrm{K}}$
[JEE-Main-2017]
Ans. (3)
Due to thermal expansion
$\frac{\Delta \mathrm{v}}{\mathrm{v}}=3 \alpha \Delta \mathrm{T}$
Due to External pressure
$\frac{\Delta \mathrm{v}}{\mathrm{v}}=\frac{\mathrm{P}}{\mathrm{K}}$