JEE Advanced Previous Year Questions of Physics with Solutions are available at eSaral. Practicing JEE Advanced Previous Year Papers Questions of Physics will help the JEE aspirants in realizing the question pattern as well as help in analyzing weak & strong areas.
Get detailed Class 11th & 12th Physics Notes to prepare for Boards as well as competitive exams like IIT JEE, NEET etc.
eSaral helps the students in clearing and understanding each topic in a better way. eSaral is providing complete chapter-wise notes of Class 11th and 12th both for all subjects.
Click Here for JEE main Previous Year Topic Wise Questions of Physics with Solutions
Download eSaral app for free study material and video tutorials.
Simulator
Previous Years JEE Advanced Questions
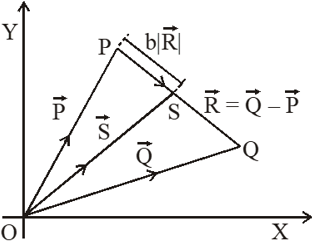
Q. Three vectors $\overrightarrow{\mathrm{P}}, \overrightarrow{\mathrm{Q}}$ and $\overrightarrow{\mathrm{R}}$ are shown in the figure. Let S be any point on the vector $\overrightarrow{\mathrm{R}}$. The distance between the points P and S is b $|\overrightarrow{\mathrm{R}}|$. The general relation among vectors $\overrightarrow{\mathrm{P}}, \overrightarrow{\mathrm{Q}}$ and $\overrightarrow{\mathrm{S}}$ is :
$(\mathrm{A}) \overrightarrow{\mathrm{S}}=(1-\mathrm{b}) \overrightarrow{\mathrm{P}}+\mathrm{b}^{2} \overrightarrow{\mathrm{Q}}$
(B) $\overrightarrow{\mathrm{S}}=(b-1) \overrightarrow{\mathrm{P}}+b \overrightarrow{\mathrm{Q}}$
(C) $\overrightarrow{\mathrm{S}}=(1-\mathrm{b}) \overrightarrow{\mathrm{P}}+\mathrm{b} \overrightarrow{\mathrm{Q}}$
$(\mathrm{D}) \overrightarrow{\mathrm{S}}=\left(1-\mathrm{b}^{2}\right) \overrightarrow{\mathrm{P}}+\mathrm{b} \overrightarrow{\mathrm{Q}}$
[JEE Advanced - 2017]
$(\mathrm{A}) \overrightarrow{\mathrm{S}}=(1-\mathrm{b}) \overrightarrow{\mathrm{P}}+\mathrm{b}^{2} \overrightarrow{\mathrm{Q}}$
(B) $\overrightarrow{\mathrm{S}}=(b-1) \overrightarrow{\mathrm{P}}+b \overrightarrow{\mathrm{Q}}$
(C) $\overrightarrow{\mathrm{S}}=(1-\mathrm{b}) \overrightarrow{\mathrm{P}}+\mathrm{b} \overrightarrow{\mathrm{Q}}$
$(\mathrm{D}) \overrightarrow{\mathrm{S}}=\left(1-\mathrm{b}^{2}\right) \overrightarrow{\mathrm{P}}+\mathrm{b} \overrightarrow{\mathrm{Q}}$
[JEE Advanced - 2017]
Ans. (C)
Let vector from point P to point S be $\overrightarrow{\mathrm{c}}$
$\Rightarrow \overrightarrow{\mathrm{c}}=\mathrm{b}|\overrightarrow{\mathrm{R}}| \hat{\mathrm{R}}=\mathrm{b}|\overrightarrow{\mathrm{R}}|\left(\frac{\overrightarrow{\mathrm{R}}}{|\overrightarrow{\mathrm{R}}|}\right)=\mathrm{b} \overrightarrow{\mathrm{R}}=\mathrm{b}(\overrightarrow{\mathrm{Q}}-\overrightarrow{\mathrm{P}})$
from triangle rule of vector addition
$\overrightarrow{\mathrm{P}}+\overrightarrow{\mathrm{C}}=\overrightarrow{\mathrm{S}}$
$\overrightarrow{\mathrm{P}}+\mathrm{b}(\overrightarrow{\mathrm{Q}}-\overrightarrow{\mathrm{P}})=\overrightarrow{\mathrm{S}}$
$\Rightarrow \overrightarrow{\mathrm{S}}=(1-\mathrm{b}) \overrightarrow{\mathrm{P}}+\mathrm{b} \overrightarrow{\mathrm{Q}}$
Q. Consider an expanding sphere of instantaneous radius R whose total mass remains constant. The expansion is such that the instantaneous density remains uniform throughout the volume. The rate of fractional change in density $\left(\frac{1}{\rho} \frac{\mathrm{d} \rho}{\mathrm{dt}}\right)$ is constant. The velocity v of any point on the surface of the expanding sphere is proportional to :
(A) $\mathrm{R}^{3}$
(B) $\frac{1}{\mathrm{R}}$
(C) R
(D) $\mathrm{R}^{2 / 3}$
[JEE Advanced - 2017]
Ans. (C)
Density of sphere is $\rho=\frac{\mathrm{m}}{\mathrm{v}}=\frac{3 \mathrm{m}}{4 \pi \mathrm{R}^{3}}$
$\Rightarrow \frac{1}{\rho} \frac{\mathrm{d} \rho}{\mathrm{dt}}=-\frac{3}{\mathrm{R}} \frac{\mathrm{d} \mathrm{R}}{\mathrm{dt}}$
since $\Rightarrow \frac{1}{\rho} \frac{\mathrm{d} \rho}{\mathrm{dt}}$ is constant
$\therefore \frac{\mathrm{d} \mathrm{R}}{\mathrm{dt}} \propto \mathrm{R}$
Velocity of any point on the circumfrence V is equal to $\frac{\mathrm{d} \mathrm{R}}{\mathrm{dt}}$ (rate of change of radius of outer layer)