JEE Advanced Previous Year Questions of Math with Solutions are available at eSaral. Practicing JEE Advanced Previous Year Papers Questions of mathematics will help the JEE aspirants in realizing the question pattern as well as help in analyzing weak & strong areas.
eSaral helps the students in clearing and understanding each topic in a better way. eSaral also provides complete chapter-wise notes of Class 11th and 12th both for all subjects.
Besides this, eSaral also offers NCERT Solutions, Previous year questions for JEE Main and Advance, Practice questions, Test Series for JEE Main, JEE Advanced and NEET, Important questions of Physics, Chemistry, Math, and Biology and many more.
Download eSaral app for free study material and video tutorials.
Let O be the origin, and $\overrightarrow{\mathrm{OX}}, \overrightarrow{\mathrm{OY}}, \overrightarrow{\mathrm{OZ}}$ be three unit vectors in the directions of the sides $\overrightarrow{\mathrm{QR}}, \overrightarrow{\mathrm{RP}}, \overrightarrow{\mathrm{PQ}},$ respectively, of a triangle $\mathrm{PQR}$
Q. (A) If $\vec{a}, \vec{b}, \vec{c}$ and $\vec{d}$ are unit vectors such that $(\vec{a} \times \vec{b}) \cdot(\vec{c} \times \vec{d})=1$ and $\vec{a} \cdot \vec{c}=\frac{1}{2},$ then $-$
(A) $\overrightarrow{\mathrm{a}}, \overrightarrow{\mathrm{b}}, \overrightarrow{\mathrm{c}}$ are non-coplanar
(B) $\overrightarrow{\mathrm{b}}, \overrightarrow{\mathrm{c}}, \overrightarrow{\mathrm{d}}$ are non-coplanar
(C) $\overrightarrow{\mathrm{b}}, \overrightarrow{\mathrm{d}}$ arenon-parallel
(D) $\overrightarrow{\mathrm{a}}, \overrightarrow{\mathrm{d}}$ are parallel and $\overrightarrow{\mathrm{b}}, \overrightarrow{\mathrm{c}}$ are parallel
(B) Match the statements / expressions given in Column I with the values given in Column II.
[JEE 2009, 3+8]
[JEE 2009, 3+8]
Ans. ((A) C (B) (A) Q,S (B) P,R,S,T (C) T (D) R )
(A) Let angle between $\overrightarrow{\mathrm{a}}$ and $\overrightarrow{\mathrm{b}}$ be $\theta_{1}, \overrightarrow{\mathrm{c}}$ and $\overrightarrow{\mathrm{d}}$ be $\theta_{2}$ and $\overrightarrow{\mathrm{a}} \times \overrightarrow{\mathrm{b}}$ and $\overrightarrow{\mathrm{c}} \times \overrightarrow{\mathrm{d}}$ be $\theta$
since $(\vec{a} \times \vec{b}) .(\vec{c} \times \vec{d})=1$
$\sin \theta_{1} \sin \theta_{2} \cos \theta=1$
$\theta_{1}=90, \theta_{2}=90, \theta=0$
$\overrightarrow{\mathrm{a}} \perp \overrightarrow{\mathrm{b}}, \overrightarrow{\mathrm{c}} \perp \overrightarrow{\mathrm{d}},(\overrightarrow{\mathrm{a}} \times \overrightarrow{\mathrm{b}}) \|(\overrightarrow{\mathrm{c}} \times \overrightarrow{\mathrm{d}})$
so $\overrightarrow{\mathrm{a}} \times \overrightarrow{\mathrm{b}}=\mathrm{k}(\overrightarrow{\mathrm{c}} \times \overrightarrow{\mathrm{d}})$
and $\quad(\overrightarrow{\mathrm{a}} \times \overrightarrow{\mathrm{b}}) \cdot \overrightarrow{\mathrm{c}}=\mathrm{k}(\overrightarrow{\mathrm{c}} \times \overrightarrow{\mathrm{d}}) \cdot \overrightarrow{\mathrm{c}}$
Case I $(\vec{a} \times \vec{b}) \cdot \vec{d}=k(\vec{c} \times \vec{d}) . \vec{d} \quad \because[\vec{a} \vec{b} \vec{c}]=0$
Case II $\overrightarrow{\mathrm{b}} \cdot(\overrightarrow{\mathrm{a}} \times \overrightarrow{\mathrm{b}})=\mathrm{k} \overrightarrow{\mathrm{b}} \cdot(\overrightarrow{\mathrm{c}} \times \overrightarrow{\mathrm{d}}) \therefore[\overrightarrow{\mathrm{b}} \overrightarrow{\mathrm{c}} \cdot \overrightarrow{\mathrm{d}}]=0$
(A) and (B) are in correct
let $\overrightarrow{\mathrm{b}} \| \overrightarrow{\mathrm{d}} \Rightarrow \overrightarrow{\mathrm{b}}=\pm \overrightarrow{\mathrm{d}}$
As $(\overrightarrow{\mathrm{a}} \times \overrightarrow{\mathrm{b}}) \cdot(\overrightarrow{\mathrm{c}} \times \overrightarrow{\mathrm{d}})=1$
$\Rightarrow(\vec{a} \times \vec{b}) \cdot(\vec{c} \times \vec{b})=\pm 1$
$[\overrightarrow{\mathrm{a}} \times \overrightarrow{\mathrm{b}} \overrightarrow{\mathrm{c}} \overrightarrow{\mathrm{b}}]=\pm 1$
$[\overrightarrow{\mathrm{c}} \quad \overrightarrow{\mathrm{b}} \quad \overrightarrow{\mathrm{a}} \times \overrightarrow{\mathrm{b}}]=\pm 1$
$\overrightarrow{\mathrm{c}} \cdot[\overrightarrow{\mathrm{b}} \times(\overrightarrow{\mathrm{a}} \times \overrightarrow{\mathrm{b}})]=\pm 1$
$\overrightarrow{\mathrm{c}} \cdot[\overrightarrow{\mathrm{a}}-(\overrightarrow{\mathrm{b}} \cdot \overrightarrow{\mathrm{a}}) \overrightarrow{\mathrm{b}}]=\pm 1$
$\overrightarrow{\mathrm{c} .} \overrightarrow{\mathrm{a}}=\pm 1 \quad \because \quad \overrightarrow{\mathrm{a}} \cdot \overrightarrow{\mathrm{b}}=0$
Which is contradiction so option (c) is correct let option (d) is correct
$\overrightarrow{\mathrm{d}}=\pm \overrightarrow{\mathrm{a}}$ and $\overrightarrow{\mathrm{c}}=\pm \overrightarrow{\mathrm{b}}$
$(\vec{a} \times \vec{b}) \cdot(\vec{c} \times \vec{d})=1$
$(\vec{a} \times \vec{b}) \cdot(\vec{b} \times \vec{a})=\pm 1$
so (d) incorrect
(B) $(\mathrm{A}) 2 \sin ^{2} \theta+\sin ^{2} 2 \theta=2$
$\sin ^{2} 2 \theta=2 \cos ^{2} \theta$
$4 \sin ^{2} \theta \cos ^{2} \theta=2 \cos ^{2} \theta$
$\cos ^{2} \theta=0$ or $\sin ^{2} \theta=\frac{1}{2}$
$\theta=\frac{\pi}{2}$ or $\sin 0=\pm \frac{1}{\sqrt{2}}$
$\theta=\frac{\pi}{2}, \pm \frac{\pi}{4}$
(B) $\mathrm{f}(\mathrm{x})=\left[\frac{6 \mathrm{x}}{\pi}\right] \cos \left[\frac{3 \mathrm{x}}{\pi}\right]$
possible point of discontinuty of $\left[\frac{6 \mathrm{x}}{\pi}\right]$
$\frac{6 \mathrm{x}}{\pi}=\mathrm{n}, \mathrm{n} \in \mathrm{I}$
$x=\frac{n \pi}{6}$
$\Rightarrow \mathrm{x}=\frac{\pi}{6}, \frac{\pi}{3}, \frac{\pi}{2}, \pi$
Lt $f(x)=1 \cos 0=1$
$\mathrm{x} \rightarrow \frac{\pi^{+}}{6}$
$\mathrm{Lt}-\mathrm{f}(\mathrm{x})=0 \cos 0=0$
$\mathrm{X} \rightarrow \frac{\pi^{-}}{6}$
disconti at $x=\frac{\pi}{6}$
similarly $x=\frac{\pi}{3}, \frac{\pi}{2}, \pi$
(C) Here $\mathrm{v}=\left|\begin{array}{ccc}{1} & {1} & {0} \\ {1} & {2} & {0} \\ {1} & {1} & {\pi}\end{array}\right|=\pi \mathrm{cm}^{3}$
(d) Given $\overrightarrow{\mathrm{a}}+\overrightarrow{\mathrm{b}}+\sqrt{3} \overrightarrow{\mathrm{c}}=0$
$\overrightarrow{\mathrm{a}}+\overrightarrow{\mathrm{b}}=-\sqrt{3} \overrightarrow{\mathrm{c}}$
$|\overrightarrow{\mathrm{a}}+\overrightarrow{\mathrm{b}}|^{2}=|\sqrt{3} \overrightarrow{\mathrm{c}}|^{2}$
$a^{2}+b^{2}+2 \vec{a} \cdot \vec{b}=3 c^{2}$
$2+\cos \theta=3$
$\cos \theta=\frac{1}{2}$
$\theta=\frac{\pi}{3}$
Q. (A) Two adjacent sides of a parallelogram ABCD are given by $\overrightarrow{\mathrm{AB}}=2 \hat{\mathrm{i}}+10 \hat{\mathrm{j}}+11 \hat{\mathrm{k}}$ and $\overrightarrow{\mathrm{AD}}=-\hat{\mathrm{i}}+2 \hat{\mathrm{j}}+2 \hat{\mathrm{k}} .$ The side $\mathrm{AD}$ is rotated by an acute angle $\alpha$ in the plane of the parallelogram so that AD becomes AD'. If AD' makes a right angle with the side AB, then the cosine of the angle $\alpha$ is given by –
(A) $\frac{8}{9}$
(B) $\frac{\sqrt{17}}{9}$
(C) $\frac{1}{9}$
(D) $\frac{4 \sqrt{5}}{9}$
(B) If $\vec{a}$ and $\vec{b}$ are vectors in space given by $\vec{a}=\frac{\hat{i}-2 \hat{j}}{\sqrt{5}}$ and $\vec{b}=\frac{2 \hat{i}+\hat{j}+3 \hat{k}}{\sqrt{14}},$ then the value of $(2 \vec{a}+\vec{b}) \cdot[(\vec{a} \times \vec{b}) \times(\vec{a}-2 \vec{b})]$ is
[JEE 2010, 5+3]
Ans. ( (A) B (B) 5 )
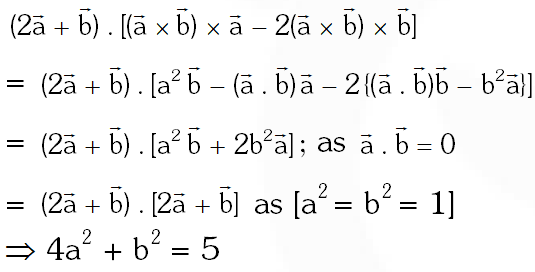
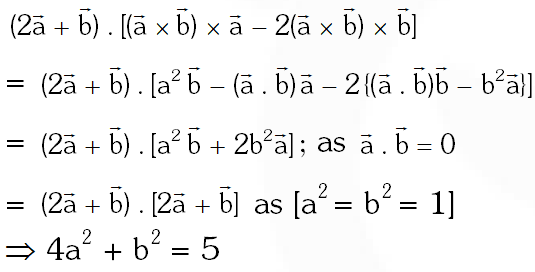
Q. (A) Let $\vec{a}=\hat{i}+\hat{j}+\hat{k}, \vec{b}=\hat{i}-\hat{j}+\hat{k}$ and $\vec{c}=\hat{i}-\hat{j}-\hat{k}$ be three vectors. A vector $\vec{v}$ in the plane of $\overrightarrow{\mathrm{a}}$ and $\overrightarrow{\mathrm{b}},$ whose projection on $\overrightarrow{\mathrm{c}}$ is $\frac{1}{\sqrt{3}},$ is given by
(A) $\hat{\mathrm{i}}-3 \hat{\mathrm{j}}+3 \hat{\mathrm{k}}$
(B) $-3 \hat{\mathrm{i}}-3 \hat{\mathrm{j}}-\hat{\mathrm{k}}$
(C) $3 \hat{\mathrm{i}}-\hat{\mathrm{j}}+3 \hat{\mathrm{k}}$
(D) $\hat{\mathrm{i}}+3 \hat{\mathrm{j}}-3 \hat{\mathrm{k}}$
(B) The vector(s) which is/are coplanar with vectors $\hat{\mathrm{i}}+\hat{\mathrm{j}}+2 \hat{\mathrm{k}}$ and $\hat{\mathrm{i}}+2 \hat{\mathrm{j}}+\hat{\mathrm{k}},$ and perpendicular to the vector $\hat{\mathrm{i}}+\hat{\mathrm{j}}+\hat{\mathrm{k}}$ is/are
(A) $\hat{\mathrm{j}}-\hat{\mathrm{k}}$
(B) $-\hat{\hat{\mathrm{i}}}+\hat{\hat{\mathrm{j}}}$
(C) $\hat{\mathrm{i}}-\hat{\mathrm{j}}$
$(D)-\hat{j}+\hat{k}$
(C) Let $\vec{a}=-\hat{i}-\hat{k}, \vec{b}=-\hat{i}+\hat{j}$ and $\vec{c}=\hat{i}+2 \hat{j}+3 \hat{k}$ be three given vectors. If $\vec{r}$ is a vector such that $\overrightarrow{\mathrm{r}} \times \overrightarrow{\mathrm{b}}=\overrightarrow{\mathrm{c}} \times \overrightarrow{\mathrm{b}}$ and $\overrightarrow{\mathrm{r} .} \overrightarrow{\mathrm{a}}=0,$ then the value of $\overrightarrow{\mathrm{r}} . \overrightarrow{\mathrm{b}}$ is
[JEE 2011, 3+4+4]
Ans. ( (A) C (B) A,D (C) 9 )
$\overrightarrow{\mathrm{v}}=\mathrm{x} \overrightarrow{\mathrm{a}}+\mathrm{y} \overrightarrow{\mathrm{b}}$
$=\hat{\mathbf{i}}(\mathrm{x}+\mathrm{y})+\hat{\mathrm{j}}(\mathrm{x}-\mathrm{y})+\hat{\mathrm{k}}(\mathrm{x}+\mathrm{y}) \ldots .(\mathrm{i})$
Given $, \overrightarrow{\mathrm{v}} . \hat{\mathrm{c}}=\frac{1}{\sqrt{3}}$
$\Rightarrow \frac{x+y-x+y-x-y}{\sqrt{3}}=\frac{1}{\sqrt{3}}$
$\mathrm{y}-\mathrm{x}=1$
$\Rightarrow \mathrm{x}-\mathrm{y}=-1$
using (ii) in (i) we get $\overrightarrow{\mathrm{v}}=(\mathrm{x}+\mathrm{y}) \hat{\mathrm{i}}-\hat{\mathrm{j}}+(\mathrm{x}+\mathrm{y}) \hat{\mathrm{k}}$
(b) $\vec{a}=\hat{i}+\hat{j}+2 \hat{k}$
$\overrightarrow{\mathrm{b}}=\hat{\mathrm{i}}+2 \hat{\mathrm{j}}+\hat{\mathrm{k}}$
$\overrightarrow{\mathrm{c}}=\hat{\mathrm{i}}+\hat{\mathrm{j}}+\hat{\mathrm{k}}$
$\overrightarrow{\mathrm{v}}=\lambda((\overrightarrow{\mathrm{a}} \times \overrightarrow{\mathrm{b}}) \times \overrightarrow{\mathrm{c}})=\lambda((\overrightarrow{\mathrm{a}} \cdot \overrightarrow{\mathrm{c}}) \overrightarrow{\mathrm{b}}-(\overrightarrow{\mathrm{b}} \cdot \overrightarrow{\mathrm{c}}) \overrightarrow{\mathrm{a}}$
$\overrightarrow{\mathrm{v}}=\lambda[4(\hat{\mathrm{i}}+2 \hat{\mathrm{j}}+\hat{\mathrm{k}})-4(\hat{\mathrm{i}}+\hat{\mathrm{j}}+2 \hat{\mathrm{k}})]$
$\overrightarrow{\mathrm{v}}=4 \lambda(\hat{j}-\hat{\mathrm{k}})$
(c) $\overrightarrow{\mathrm{a}}=-\hat{\mathrm{i}}-\hat{\mathrm{k}}$
$\overrightarrow{\mathrm{b}}=-\hat{\mathrm{i}}+\hat{\mathrm{j}}$
$\overrightarrow{\mathrm{c}}=\hat{\mathrm{i}}+2 \hat{\mathrm{j}}+3 \hat{\mathrm{k}}$
$\overrightarrow{\mathrm{r}} \times \overrightarrow{\mathrm{b}}=\overrightarrow{\mathrm{c}} \times \overrightarrow{\mathrm{b}}$
Taking cross product by $\overrightarrow{\mathrm{a}}$
$(\overrightarrow{\mathrm{r}} \times \overrightarrow{\mathrm{b}}) \times \overrightarrow{\mathrm{a}}=(\overrightarrow{\mathrm{c}} \times \overrightarrow{\mathrm{b}}) \times \overrightarrow{\mathrm{a}}$
$\Rightarrow(\overrightarrow{\mathrm{r}} \cdot \overrightarrow{\mathrm{a}}) \overrightarrow{\mathrm{b}}-(\overrightarrow{\mathrm{b}} \cdot \overrightarrow{\mathrm{a}}) \overrightarrow{\mathrm{r}}=(\overrightarrow{\mathrm{c}} \cdot \overrightarrow{\mathrm{a}}) \overrightarrow{\mathrm{b}})-(\overrightarrow{\mathrm{b}} \cdot \overrightarrow{\mathrm{a}}) \overrightarrow{\mathrm{c}}$
$\Rightarrow 0-\overrightarrow{\mathrm{r}}=(-1-3)(-\hat{\mathrm{i}}+\hat{\mathrm{j}})-(1)(\hat{\mathrm{i}}+2 \hat{\mathrm{j}}+3 \hat{\mathrm{k}})$
$\overrightarrow{\mathrm{r}}=-3 \hat{\mathrm{i}}+6 \hat{\mathrm{j}}+3 \hat{\mathrm{k}}$
$\overrightarrow{\mathrm{r}} \cdot \overrightarrow{\mathrm{b}}=3+6=9$
Q. (A) If $\vec{a}, \vec{b}$ and $\vec{c}$ are unit vectors satisfying $|\vec{a}-\vec{b}|^{2}+|\vec{b}-\vec{c}|^{2}+|\vec{c}-\vec{a}|^{2}=9,$ then
\[|2 \overrightarrow{\mathrm{a}}+5 \overrightarrow{\mathrm{b}}+5 \overrightarrow{\mathrm{c}}| \text { is }\]
(B) If $\vec{a}$ and $\vec{b}$ are vectors such that $|\vec{a}+\vec{b}|=\sqrt{29}$ and $\overrightarrow{\mathrm{a}} \times(2 \hat{\mathrm{i}}+3 \hat{\mathrm{j}}+4 \hat{\mathrm{j}}+4 \hat{\mathrm{k}})=(2 \hat{\mathrm{i}}+3 \hat{\mathrm{j}}+4 \hat{\mathrm{k}}) \times \overrightarrow{\mathrm{b}},$ then a possible value of $(\overrightarrow{\mathrm{a}}+\overrightarrow{\mathrm{b}}) \cdot(-7 \hat{\mathrm{i}}+2 \hat{\mathrm{j}}+3 \hat{\mathrm{k}})$ is
(A) 0 (B) 3 (C) 4 (D) 8
[JEE 2012, 4+3]
Ans. ( (A) 3 (B) C)
$|\vec{a}-\vec{b}|^{2}+|\vec{b}-\vec{c}|^{2}+|\vec{c}-\vec{a}|^{2}=9$
$\Rightarrow 6-2 \Sigma \overrightarrow{\mathrm{a}} \cdot \overrightarrow{\mathrm{b}}=9$
$\Rightarrow \Sigma \overrightarrow{\mathrm{a}} \cdot \overrightarrow{\mathrm{b}}=-\frac{3}{2}$
$|\overrightarrow{\mathrm{a}}+\overrightarrow{\mathrm{b}}+\overrightarrow{\mathrm{c}}|^{2} \geq 0$
$\Sigma \overrightarrow{\mathrm{a}}^{2}+2 \Sigma \overrightarrow{\mathrm{a}} \cdot \overrightarrow{\mathrm{b}} \geq 0$
$\sum \overrightarrow{\mathrm{a}} \cdot \overrightarrow{\mathrm{b}} \geq-\frac{3}{2}$
for equality $|\overrightarrow{\mathrm{a}}+\overrightarrow{\mathrm{b}}+\overrightarrow{\mathrm{c}}|=0$
$\Rightarrow \overrightarrow{\mathrm{a}}+\overrightarrow{\mathrm{b}}+\overrightarrow{\mathrm{c}}=0$
$5 \overrightarrow{\mathrm{b}}+5 \overrightarrow{\mathrm{c}}=-5 \overrightarrow{\mathrm{a}}$
$2 \vec{a}+5 \vec{b}+5 \vec{c}=-3 \vec{a}$
$|2 \vec{a}+5 \vec{b}+5 \vec{c}|=3|\vec{a}|=3$
(b) $(\vec{a}+\vec{b}) \times(2 \hat{i}+3 \hat{j}+4 \hat{k})=0$
$\Rightarrow \overrightarrow{\mathrm{a}}+\overrightarrow{\mathrm{b}}=\lambda(2 \hat{\mathrm{i}}+3 \hat{\mathrm{j}}+4 \hat{\mathrm{k}})$
$|\overrightarrow{\mathrm{a}}+\overrightarrow{\mathrm{b}}|=\sqrt{29} \Rightarrow|\lambda|=1$
$\overrightarrow{\mathrm{a}}+\overrightarrow{\mathrm{b}}=(2 \hat{\mathrm{i}}+3 \hat{\mathrm{j}}+4 \hat{\mathrm{k}})$
$(\vec{a}+\vec{b}) \cdot(-7 \hat{i}+2 \hat{j}+3 \hat{k})=-14+6+12=4$
Q. Let $\overrightarrow{\mathrm{PR}}=3 \hat{\mathrm{i}}+\hat{\mathrm{j}}-2 \hat{\mathrm{k}}$ and $\overline{\mathrm{SQ}}=\hat{\mathrm{i}}-3 \hat{\mathrm{j}}-4 \hat{\mathrm{k}}$ determine diagonals of a parallelogram PQRS and $\overrightarrow{\mathrm{PT}}=\hat{\mathbf{i}}+2 \hat{\mathbf{j}}+3 \hat{\mathbf{k}}$ be another vector. Then the volume of the parallelepiped determined by the vectors $\overrightarrow{\mathrm{PT}}, \overrightarrow{\mathrm{PQ}}$ and $\overrightarrow{\mathrm{PS}}$ is
(A) 5 (B) 20 (C) 10 (D) 30
[JEE-Advanced 2013, 2M]
Ans. (C)
$\overrightarrow{\mathrm{a}}+\overrightarrow{\mathrm{b}}=\overrightarrow{\mathrm{PR}} \& \overrightarrow{\mathrm{a}}-\overrightarrow{\mathrm{b}}=\overrightarrow{\mathrm{QS}}$
$\overrightarrow{\mathrm{a}}=\frac{\overrightarrow{\mathrm{PR}}+\overrightarrow{\mathrm{QS}}}{2} \& \overrightarrow{\mathrm{b}}=\frac{\overrightarrow{\mathrm{PR}}-\overrightarrow{\mathrm{QS}}}{2}$
$\overrightarrow{\mathrm{a}}=2 \hat{\mathrm{i}}-\hat{\mathrm{j}}-3 \hat{\mathrm{k}} \& \overrightarrow{\mathrm{b}}=\hat{\mathrm{i}}+2 \hat{\mathrm{j}}+\hat{\mathrm{k}}$
Volume $=\left|\begin{array}{ccc}{2} & {-1} & {-3} \\ {1} & {2} & {1} \\ {1} & {2} & {3}\end{array}\right|$
$2(4)+(3-1)-3(2-2)$
$8+2=10$
Q. Consider the set of eight vectors $\mathrm{V}=\{\mathrm{a} \hat{\mathrm{i}}+\mathrm{b} \hat{\mathrm{j}}+\mathrm{c} \hat{\mathrm{k}}: \mathrm{a}, \mathrm{b}, \mathrm{c} \in\{-1,1\}\} .$ Three non- coplanar vectors can be chosen from $\mathrm{V}$ in $2^{\mathrm{p}}$ ways. Then $\mathrm{p}$ is
[JEE-Advanced 2013, 4, (–1)]
Ans. 5
The 8 vectors will represent $\mathrm{O}$ is at the centre of cube $\overrightarrow{\mathrm{OA}}, \overrightarrow{\mathrm{OB}} \ldots \ldots \overrightarrow{\mathrm{OD}}, \overrightarrow{\mathrm{OP}}, \ldots \ldots . \overrightarrow{\mathrm{OS}}$
ABCDPQRS any three out of these 8 will be coplanar when two of them are
There are 4 pairs of collinear vectors $\overrightarrow{\mathrm{OA}} \& \overrightarrow{\mathrm{OR}}, \overrightarrow{\mathrm{OB}} \& \overrightarrow{\mathrm{OS}}, \overrightarrow{\mathrm{OC}} \& \overrightarrow{\mathrm{OP}}, \overrightarrow{\mathrm{OD}} \& \overrightarrow{\mathrm{OQ}}$
(it will generate $4 \times 6=24$ set of coplanar vectors) rest of the combination of 3 vectors will form three edges of a tetrahedron so they will be not coplanar. So number of non-coplanar vectors $^{8} \mathrm{C}_{3}-4.6=32$
There are 4 pairs of collinear vectors $\overrightarrow{\mathrm{OA}} \& \overrightarrow{\mathrm{OR}}, \overrightarrow{\mathrm{OB}} \& \overrightarrow{\mathrm{OS}}, \overrightarrow{\mathrm{OC}} \& \overrightarrow{\mathrm{OP}}, \overrightarrow{\mathrm{OD}} \& \overrightarrow{\mathrm{OQ}}$
(it will generate $4 \times 6=24$ set of coplanar vectors) rest of the combination of 3 vectors will form three edges of a tetrahedron so they will be not coplanar. So number of non-coplanar vectors $^{8} \mathrm{C}_{3}-4.6=32$
Q. Match List-I with List-II and select the correct answer using the code given
below the lists.
[JEE-Advanced 2013, 3, (–1)]
[JEE-Advanced 2013, 3, (–1)]
Ans. (C)
(P) Given $[\overrightarrow{\mathrm{a}} \overrightarrow{\mathrm{b}} \overrightarrow{\mathrm{c}}]=2$
$[2(\vec{a} \times \vec{b}) 3(\vec{b} \times \vec{c})(\vec{c} \times \vec{a})]=6[\vec{a} \times \vec{b} \quad \vec{b} \times \vec{c} \vec{c} \times \vec{a}]$
$=6[\vec{a} \vec{b} \vec{c}]^{2}=24$
(Q) Given $[\overrightarrow{\mathrm{a}} \overrightarrow{\mathrm{b}} \overrightarrow{\mathrm{c}}]=5$
$[3(\vec{a}+\vec{b})(\vec{b}+\vec{c}) 2(\vec{c}+\vec{a})]=12[\vec{a} \vec{b} \vec{c}]=60$
(R) Given $\frac{1}{2}|\overrightarrow{\mathrm{a}} \times \overrightarrow{\mathrm{b}}|=20$
$\Rightarrow|\overrightarrow{\mathrm{a}} \times \overrightarrow{\mathrm{b}}|=40$
$\left|\frac{1}{2}(2 \vec{a}+3 \vec{b}) \times(\vec{a}-\vec{b})\right|=\frac{1}{2}|0+3 \vec{b} \times \vec{a}-2 \vec{a} \times \vec{b}|$
$=\frac{1}{2}|-5 \overrightarrow{\mathrm{a}} \times \overrightarrow{\mathrm{b}}|=\frac{5}{2}|\overrightarrow{\mathrm{a}} \times \overrightarrow{\mathrm{b}}|=\frac{5}{2} \cdot 40=100$
(S) Given $|\overrightarrow{\mathrm{a}} \times \overrightarrow{\mathrm{b}}|=30$
$|(\vec{a}+\vec{b}) \times \vec{a}|=|0+\vec{b} \times \vec{a}|=30$
Q. Let $\overrightarrow{\mathrm{x}}, \overrightarrow{\mathrm{y}}$ and $\overrightarrow{\mathrm{z}}$ be three vectors each of magnitude $\sqrt{2}$ and the angle between each pair of them is $\frac{\pi}{3} .$ If $\overrightarrow{\mathrm{a}}$ is a nonzero vector perpendicular to $\overrightarrow{\mathrm{x}}$ and $\overrightarrow{\mathrm{y}} \times \overrightarrow{\mathrm{z}}$ and $\overrightarrow{\mathrm{b}}$ is nonzero vector perpendicular to $\overrightarrow{\mathrm{y}}$ and $\overrightarrow{\mathrm{z}} \times \overrightarrow{\mathrm{x}},$ then
(A) $\overrightarrow{\mathrm{b}}=(\overrightarrow{\mathrm{b}} \cdot \overrightarrow{\mathrm{z}})(\overrightarrow{\mathrm{z}}-\overrightarrow{\mathrm{x}})$
(B) $\overrightarrow{\mathrm{a}}=(\overrightarrow{\mathrm{a}} \cdot \overrightarrow{\mathrm{y}})(\overrightarrow{\mathrm{y}}-\overrightarrow{\mathrm{z}})$
(C) $\overrightarrow{\mathrm{a}} \cdot \overrightarrow{\mathrm{b}}=-(\overrightarrow{\mathrm{a}} \cdot \overrightarrow{\mathrm{y}})(\overrightarrow{\mathrm{b}} \cdot \overrightarrow{\mathrm{z}})$
$(D) \quad \vec{a}=(\vec{a} \cdot \vec{y})(\vec{z}-\vec{y})$
[JEE(Advanced)-2014, 3]
Ans. (A,B,C)
Given that $|\overrightarrow{\mathrm{x}}|=|\overrightarrow{\mathrm{y}}|=|\overrightarrow{\mathrm{z}}|=\sqrt{2}$
and angle between each pair is $\frac{\pi}{3}$
$\therefore \overrightarrow{\mathrm{x}} \cdot \overrightarrow{\mathrm{y}}=\overrightarrow{\mathrm{y} .} \cdot \overrightarrow{\mathrm{z}}=\overrightarrow{\mathrm{z}} \cdot \overrightarrow{\mathrm{x}}=\sqrt{2} \cdot \sqrt{2} \cdot \frac{1}{2}=1$
Now $\vec{a}$ is $\perp$ to $\vec{x} \&(\vec{y} \times \vec{z})$
Let $\overrightarrow{\mathrm{a}}=\lambda(\overrightarrow{\mathrm{x}} \times(\overrightarrow{\mathrm{y}} \times \overrightarrow{\mathrm{z}}))$
$=\lambda((\overrightarrow{\mathrm{x}} \cdot \overrightarrow{\mathrm{z}}) \overrightarrow{\mathrm{y}}-(\overrightarrow{\mathrm{x}} \cdot \overrightarrow{\mathrm{y}}) \overrightarrow{\mathrm{z}})=\lambda(\overrightarrow{\mathrm{y}}-\overrightarrow{\mathrm{z}})$
$\overrightarrow{\mathrm{a}} \cdot \overrightarrow{\mathrm{y}}=\lambda(\overrightarrow{\mathrm{y}} \cdot \overrightarrow{\mathrm{y}}-\overrightarrow{\mathrm{y}} \cdot \overrightarrow{\mathrm{z}})=\lambda(2-1)=\lambda$
$\Rightarrow \overrightarrow{\mathrm{a}}=(\overrightarrow{\mathrm{a}} \cdot \overrightarrow{\mathrm{y}})(\overrightarrow{\mathrm{y}}-\overrightarrow{\mathrm{z}})$
Now let $\overrightarrow{\mathrm{b}}=\mu(\overrightarrow{\mathrm{y}} \times(\overrightarrow{\mathrm{z}} \times \overrightarrow{\mathrm{x}}))=\mu(\overrightarrow{\mathrm{z}}-\overrightarrow{\mathrm{x}})$
$\overrightarrow{\mathrm{b}} \cdot \overrightarrow{\mathrm{z}}=\mu(2-1)=\mu$
$\Rightarrow \overrightarrow{\mathrm{b}}=(\overrightarrow{\mathrm{b}} \cdot \overrightarrow{\mathrm{z}})(\overrightarrow{\mathrm{z}}-\overrightarrow{\mathrm{x}})$
Now $\vec{a} \cdot \vec{b}=(\vec{a} \cdot \vec{y})(\vec{y}-\vec{z}) \cdot(\vec{b} \cdot \vec{z})(\vec{z}-\vec{x})$
$=(\vec{a} \cdot \vec{y})(\vec{b} \cdot \vec{z})(\vec{y} \cdot \vec{z}-\vec{y} \cdot \vec{x}-\vec{z} \cdot \vec{z}+\vec{z} \cdot \vec{x})$
$=(\vec{a} \cdot \vec{y})(\vec{b} \cdot \vec{z})(1-1-2+1)$
$=-(\overrightarrow{\mathrm{a}} \cdot \overrightarrow{\mathrm{y}})(\overrightarrow{\mathrm{b}} \cdot \overrightarrow{\mathrm{z}})$
Q. Let $\overrightarrow{\mathrm{a}}, \overrightarrow{\mathrm{b}},$ and $\overrightarrow{\mathrm{c}}$ be three non-coplanar unit vectors such the angle between every pair of them is $\frac{\pi}{3} \cdot$ If $\overrightarrow{\mathrm{a}} \times \overrightarrow{\mathrm{b}}+\overrightarrow{\mathrm{b}} \times \overrightarrow{\mathrm{c}}=\mathrm{p} \overrightarrow{\mathrm{a}}+\mathrm{qb}+\mathrm{r} \overrightarrow{\mathrm{c}},$ where $\mathrm{p}, \mathrm{q}$ and $\mathrm{r}$ are scalars, then the value of
$\frac{\mathrm{p}^{2}+2 \mathrm{q}^{2}+\mathrm{r}^{2}}{\mathrm{q}^{2}}$ is
[JEE(Advanced)-2014, 3]
Ans. 4
Q. Let $\Delta \mathrm{PQR}$ be a triangle. Let $\overrightarrow{\mathrm{a}}=\overrightarrow{\mathrm{QR}}, \overrightarrow{\mathrm{b}}=\overrightarrow{\mathrm{RP}}$ and $\overrightarrow{\mathrm{c}}=\overrightarrow{\mathrm{PQ}} .$ If $|\overrightarrow{\mathrm{a}}|=4 \sqrt{3}$ and $\overrightarrow{\mathrm{b} . \overrightarrow{\mathrm{c}}}=24$ then which of the following is (are) true?
(A) $\frac{|\overrightarrow{\mathrm{c}}|^{2}}{2}-|\overrightarrow{\mathrm{a}}|=12$
(B) $\frac{|\overrightarrow{\mathrm{c}}|^{2}}{2}+|\overrightarrow{\mathrm{a}}|=30$
(C) $|\overrightarrow{\mathrm{a}} \times \overrightarrow{\mathrm{b}}+\overrightarrow{\mathrm{c}} \times \overrightarrow{\mathrm{a}}|=48 \sqrt{3}$
(D) $\overrightarrow{\mathrm{a}} \cdot \overrightarrow{\mathrm{b}}=-72$
[JEE 2015, 4M, –2M]
Ans. (A,C,D)
Q. Suppose that $\overrightarrow{\mathrm{p}}, \overrightarrow{\mathrm{q}}$ and $\overrightarrow{\mathrm{r}}$ are three non-coplanar vectors in $\mathrm{U}^{3} .$ Let the components of a vector $\overrightarrow{\mathrm{s}}$ along $\overrightarrow{\mathrm{p}}, \overrightarrow{\mathrm{q}}$ and $\overrightarrow{\mathrm{r}}$ be $4,3$ and $5,$ respectively. If the components of this vector $\overrightarrow{\mathrm{s}}$ along $(-\overrightarrow{\mathrm{p}}+\overrightarrow{\mathrm{q}}+\overrightarrow{\mathrm{r}}),(\overrightarrow{\mathrm{p}}-\overrightarrow{\mathrm{q}}+\overrightarrow{\mathrm{r}})$ and $(-\overrightarrow{\mathrm{p}}-\overrightarrow{\mathrm{q}}+\overrightarrow{\mathrm{r}})$ are $\mathrm{x}, \mathrm{y}$ and $\mathrm{z},$ respectively, then the value of $2 \mathrm{x}+\mathrm{y}+\mathrm{z}$ is
[JEE 2015, 4M, –0M]
Ans. (Bonus)
Although the language of the question is not appropriate (in complete information) and it must be declare as bonus but as per the theme of problem it must be as follows
$\overrightarrow{\mathrm{s}}=4 \overrightarrow{\mathrm{p}}+3 \overrightarrow{\mathrm{q}}+5 \overrightarrow{\mathrm{r}}$
$\overrightarrow{\mathrm{s}}=\mathrm{x}(-\overrightarrow{\mathrm{p}}+\overrightarrow{\mathrm{q}}+\overrightarrow{\mathrm{r}})+\mathrm{y}(\overrightarrow{\mathrm{p}}-\overrightarrow{\mathrm{q}}+\overrightarrow{\mathrm{r}})+\mathrm{z}(-\overrightarrow{\mathrm{p}}-\overrightarrow{\mathrm{q}}+\overrightarrow{\mathrm{r}})$
$\overrightarrow{\mathrm{s}}=\overrightarrow{\mathrm{p}}(-\mathrm{x}+\mathrm{y}-\mathrm{z})+\overrightarrow{\mathrm{q}}(\mathrm{x}-\mathrm{y}-\mathrm{z})+\overrightarrow{\mathrm{r}}(\mathrm{x}+\mathrm{y}+\mathrm{z})$
$-x+y-z=4$
$x-y-z=3$
$x+y+z=5$
$\Rightarrow \mathrm{x}=4, \mathrm{y}=\frac{9}{2}, \mathrm{z}=-\frac{7}{2}$
$\Rightarrow 2 \mathrm{x}+\mathrm{y}+\mathrm{z}=8-\frac{7}{2}+\frac{9}{2}=9$
Q. Let $\hat{\mathbf{u}}=\mathbf{u}_{1} \hat{\mathbf{i}}+\mathbf{u}_{2} \hat{\mathbf{j}}+\mathbf{u}_{3} \hat{\mathbf{k}}$ be a unit vector in $\mathbb{U}^{2}$ and $\hat{\mathbf{w}}=\frac{1}{\sqrt{6}}(\hat{\mathbf{i}}+\hat{\mathbf{j}}+2 \hat{\mathbf{k}}) .$ Given that there exists a vector $\overrightarrow{\mathrm{v}}$ in $\square^{3}$ such that $|\hat{\mathrm{u}} \times \overrightarrow{\mathrm{v}}|=1$ and $\hat{\mathrm{w}} .(\hat{\mathrm{u}} \times \overrightarrow{\mathrm{v}})=1 .$ Which of the following statement(s) is(are) correct?
(A) There is exactly one choice for such $\overrightarrow{\mathrm{v}}$
(B) There are infinitely many choice for such $\overrightarrow{\mathrm{v}}$
(C) If \hat{u lies in the xy-plane then } $\left|\mathrm{u}_{1}\right|=\left|\mathrm{u}_{2}\right|$
(D) If ú lies in the xz-plane then $2\left|u_{1}\right|=\left|u_{3}\right|$
[JEE(Advanced) 2016]
Ans. (B,C)
Q. Let O be the origin and let PQR be an arbitrary triangle. The point $\mathrm{S}$ is such that $\overrightarrow{\mathrm{OP}} \cdot \overrightarrow{\mathrm{OP}}+\overrightarrow{\mathrm{OR}} \cdot \overrightarrow{\mathrm{OP}}=\overrightarrow{\mathrm{OR}} \cdot \overrightarrow{\mathrm{OP}}+\overrightarrow{\mathrm{OQ}} \cdot \overrightarrow{\mathrm{OS}}=\overrightarrow{\mathrm{OQ}} \cdot \overrightarrow{\mathrm{OR}}+\overrightarrow{\mathrm{OP}} \cdot \overrightarrow{\mathrm{OS}}$ Then the triangle PQR has S as its
(A) incentre
(B) orthocenter
(C) circumcentre
(D) centroid
[JEE(Advanced) 2017]
Ans. (B)
Let position vector of $\mathrm{P}(\overrightarrow{\mathrm{p}}), \mathrm{Q}(\overrightarrow{\mathrm{q}}), \mathrm{R}(\overrightarrow{\mathrm{r}}) \& \mathrm{S}(\overrightarrow{\mathrm{r}})$ with respect to $\mathrm{O}(\overrightarrow{\mathrm{o}})$
Now, $\overrightarrow{\mathrm{OP}} \cdot \overrightarrow{\mathrm{OQ}}+\overrightarrow{\mathrm{OR}} \cdot \overrightarrow{\mathrm{OS}}=\overrightarrow{\mathrm{OR}} \cdot \overrightarrow{\mathrm{OP}}+\overrightarrow{\mathrm{OQ}} \cdot \overrightarrow{\mathrm{OS}}$
$\Rightarrow \overrightarrow{\mathrm{p}} \cdot \overrightarrow{\mathrm{q}}+\overrightarrow{\mathrm{r}} \cdot \overrightarrow{\mathrm{s}}=\overrightarrow{\mathrm{r}} \cdot \overrightarrow{\mathrm{p}}+\overrightarrow{\mathrm{q}} \cdot \overrightarrow{\mathrm{s}}$
$\Rightarrow(\overrightarrow{\mathrm{p}}-\overrightarrow{\mathrm{s}}) \cdot(\overrightarrow{\mathrm{q}}-\overrightarrow{\mathrm{r}})=0$ .....(1)
Also, $\overrightarrow{\mathrm{OR}} \cdot \overrightarrow{\mathrm{OP}}+\overrightarrow{\mathrm{OQ}} \cdot \overrightarrow{\mathrm{OS}}=\overrightarrow{\mathrm{OQ}} \cdot \overrightarrow{\mathrm{OR}}+\overrightarrow{\mathrm{OP}} \cdot \overrightarrow{\mathrm{OS}}$
$\Rightarrow \overrightarrow{\mathrm{r}} \cdot \overrightarrow{\mathrm{p}}+\overrightarrow{\mathrm{q}} \cdot \overrightarrow{\mathrm{s}}=\overrightarrow{\mathrm{q}} \cdot \overrightarrow{\mathrm{r}}+\overrightarrow{\mathrm{p}} \cdot \overrightarrow{\mathrm{s}}$
\[ \Rightarrow(\overrightarrow{\mathrm{r}}-\overrightarrow{\mathrm{s}}) \cdot(\overrightarrow{\mathrm{p}}-\overrightarrow{\mathrm{q}})=0 \] ......(2)
Q. $|\overrightarrow{\mathrm{OX}} \times \overrightarrow{\mathrm{OY}}|=$
(A) sin(Q + R)
(B) sin(P + R)
(C) sin 2R
(D) sin(P + Q)
[JEE(Advanced) 2017]
Ans. (D)
$\overrightarrow{\mathrm{OX}}=\frac{\overrightarrow{\mathrm{QR}}}{\mathrm{QR}}$
$\overrightarrow{\mathrm{OY}}=\frac{\overrightarrow{\mathrm{RP}}}{\mathrm{RP}}$
$|\overrightarrow{\mathrm{OX}} \times \overrightarrow{\mathrm{OY}}|=\sin \mathrm{R}=\sin (\mathrm{P}+\mathrm{Q})$
Q. If the triangle PQR varies, then the minimum value of cos(P + Q) + cos(Q + R) + cos(R + P) is
[JEE(Advanced) 2017]
[JEE(Advanced) 2017]
Ans. (B)
$-(\cos P+\cos Q+\cos R) \geq-\frac{3}{2}$ as we know $\cos P+\cos Q+$ cosR will take
its maximum value when $\mathrm{P}=\mathrm{Q}=\mathrm{R}=\frac{\pi}{3}$
Q. Let $\vec{a}$ and $\vec{b}$ be two unit vectors such that $\vec{a} . \vec{b}=0 .$ For some $\mathbf{x}, y \in \square,$ let $\vec{c}=x \vec{a}+y \vec{b}+(\vec{a} \times \vec{b})$ If $|\overrightarrow{\mathrm{c}}|=2$ and the vector $\overrightarrow{\mathrm{c}}$ is inclined at the same angle $\alpha$ to both $\overrightarrow{\mathrm{a}}$ and $\overrightarrow{\mathrm{b}},$ then the value of $8 \cos ^{2} \alpha$ is
[JEE(Advanced) 2018]
Ans. 3
$\overrightarrow{\mathrm{c}}=\mathrm{x} \overrightarrow{\mathrm{a}}+\mathrm{y} \overrightarrow{\mathrm{b}}+\overrightarrow{\mathrm{a}} \times \overrightarrow{\mathrm{b}}$
$\overrightarrow{\mathrm{c}} \cdot \overrightarrow{\mathrm{a}}=\mathrm{x}$ and $\mathrm{x}=2 \cos \alpha$
$\overrightarrow{\mathrm{c}} \cdot \overrightarrow{\mathrm{b}}=\mathrm{y}$ and $\mathrm{y}=2 \cos \alpha$
Also, $|\overrightarrow{\mathrm{a}} \times \overrightarrow{\mathrm{b}}|=1$
$\begin{aligned} \therefore \quad & \overrightarrow{\mathrm{c}}=2 \cos (\overrightarrow{\mathrm{a}}+\overrightarrow{\mathrm{b}})+\overrightarrow{\mathrm{a}} \times \overrightarrow{\mathrm{b}} \\ \overrightarrow{\mathrm{c}}^{2} &=4 \cos ^{2} \alpha(\overrightarrow{\mathrm{a}}+\overrightarrow{\mathrm{b}})^{2}+(\overrightarrow{\mathrm{a}} \times \overrightarrow{\mathrm{b}})^{2}+2 \cos \alpha(\overrightarrow{\mathrm{a}}+\overrightarrow{\mathrm{b}}) \cdot(\overrightarrow{\mathrm{a}} \times \overrightarrow{\mathrm{b}}) \\ & 4=8 \cos ^{2} \alpha+1 \\ & 8 \cos ^{2} \alpha=3 \end{aligned}$
Comments
Nishu
Sept. 24, 2021, 8:05 p.m.
Really helpful .. thank you eSaral
I wish there would be some gap it's bit confusing
Thank you 😊