Vibration Magnetometer
It is an instrument used to compare magnetic moments of two bar magnets, comparison of horizontal components of earth's magnetic field at two places and for measuring the horizontal component of earth's magnet field.Principle
When a bar magnet suspended freely in a uniform magnetic field is displaced from its equilibrium position it starts executing simple harmonic motion about the equilibrium position. The torque acting on magnet is $\tau=-m B_{H}(2 \ell \sin \theta)=$ $- MB _{ H } \sin \theta$ –ive sign shows that torque acts in the direction of decreasing $\theta$. If $\theta$ is small $\tau=- MB _{ H } \theta$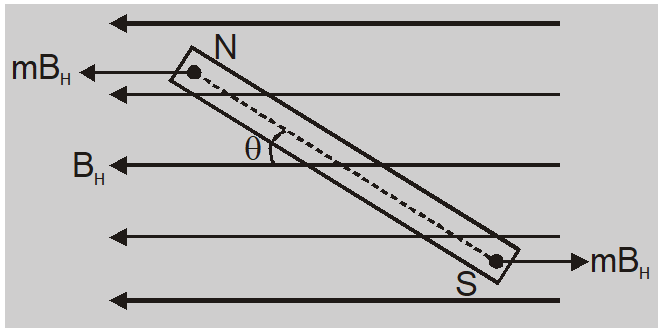
If $\alpha$ is angular acceleration of magnet and $\mathbf{I}$ is moment of inertia of magnet about axis of suspension then $I \alpha=- MB _{ H } \theta$
Time period $T =2 \pi \sqrt{\frac{\text { Angular displacement }}{\text { Angular acceleration }}}=2 \pi \sqrt{\frac{ I }{ MB _{ H }}}$
1. Comparison of Magnetic Moments of Magnets of same size: Let two magnets be of same mass and size. Let $M_{1}$ and $M_{2}$ be the magnetic moments of the magnets then time period of oscillation of each magnet is given by
$T _{1}=2 \pi \sqrt{\frac{ I }{ M _{1} B _{ H }}}$ and $T _{2}=2 \pi \sqrt{\frac{ I }{ M _{2} B _{ H }}}$
So $\frac{T_{1}}{T_{2}}=\sqrt{\frac{M_{2}}{M_{1}}}$ or $\frac{T_{1}^{2}}{T_{2}^{2}}=\frac{M_{2}}{M_{1}}=\frac{m_{2}}{m_{1}}$
2. Comparision of Magnetic Moments of Magnets of different sizes: Let two magnets have moments of inertia $I_{1}$ and $I_{2}$ and magnetic moments $M_{1}$ and $M_{2}$ respectively.
In case (a) $T _{1}=2 \pi \sqrt{\frac{ I _{1}+ I _{2}}{\left( M _{1}+ M _{2}\right) B _{ H }}}$

In case (b) $T _{2}=2 \pi \sqrt{\frac{ I _{1}+ I _{2}}{\left( M _{1}- M _{2}\right) B _{ H }}}$

So $\frac{T_{1}}{T_{2}}=\sqrt{\frac{M_{1}-M_{2}}{M_{1}+M_{2}}}$ or $\frac{T_{1}^{2}}{T_{2}^{2}}=\frac{M_{1}-M_{2}}{M_{1}+M_{2}}$ or $\frac{M_{1}}{M_{2}}=\frac{T_{1}^{2}+T_{2}^{2}}{T_{2}^{2}-T_{1}^{2}}$
Knowing $T_{1}$ and $T_{2}$ we can find $\frac{M_{1}}{M_{2}}$
3. Comparision of horizontal component of earth's magnetic field at different places : Let a magnet of moment of inertia $\mathbf{I}$ and magnetic moment M be vibrated in places with horizontal component $${B_H}\,and\,{B_H}'$$. Then
$T =2 \pi \sqrt{\frac{ I }{ MB _{ H }}}$ and $T ^{\prime}=2 \pi \sqrt{\frac{ I }{ MB _{ H }^{\prime}}}$
So $\frac{T^{\prime}}{T}=\sqrt{\frac{B_{H}}{B_{H}^{\prime}}}$ or $\frac{B_{H}}{B_{H}^{\prime}}=\frac{T^{\prime 2}}{T^{2}}$
Ex. A thin rectangular magnet suspended freely has a period of oscillation of 4 sec. What will be the period of oscillation if the magnet is broken into two halves (each having half the original length) and one of the piece is made to oscillate in the same field ? Sol. In case of torsional vibrations of magnet ; $T =2 \pi \sqrt{\frac{ I }{ MB }}$ ........(1) When the magnet is broken into equal halves perpendicular to its length, $M^{\prime}=m \times \ell=\left(\frac{M}{2}\right)$ $[\text { as } M=m \times 2 \ell]$ and, $I ^{\prime}=\frac{1}{12}(\rho S \ell) \times(\ell)^{2}=\left(\frac{ I }{8}\right)$ $\left[\text { as } I =\frac{1}{12}(2 \rho S \ell) \times(2 \ell)^{2}\right]$ So, $T ^{\prime}=2 \pi \sqrt{\frac{ T }{ M ^{\prime} B }}=2 \pi \sqrt{\frac{( I / 8)}{( M / 2) B }}=\pi \sqrt{\frac{ I }{ MB }}$........(2) And then dividing $eq ^{ n }$ (2) by (1) $\frac{ T ^{\prime}}{ T }=\frac{1}{2}$ i.e., $\quad T^{\prime}=\frac{T}{2}=\frac{4}{2}=2$ sec. Note : If the magnet is broken into two equal pieces parallel to its length, then as $M^{\prime}=\left(\frac{m}{2}\right)(2 \ell)=\frac{M}{2}$ and $I^{\prime}=\left(\frac{\text { mass }}{2}\right)(2 \ell)^{2}=\left(\frac{I}{2}\right)$ So the new time period $T^{\prime \prime}=2 \pi \sqrt{\frac{(I / 2)}{(M / 2) B}}=2 \pi \sqrt{\frac{I}{M B}}=T=4$ sec
Ex. Two bar magnets of same length and breadth but having magnetic moments M and 2M are joined together pole for pole and suspended by a string. The time of oscillation of this assembly in a magnetic field of strength B is 3 sec. What will be the period of oscillation if the polarity of one of the magnets is changed and the combination is again made to oscillate in the same field? Sol. As magnetic moment is a vector, so when magnets are joined together pole for pole M $\rightarrow$ M + 2M = 3M; so $T =2 \pi \sqrt{\frac{\left( I _{1}+ I _{2}\right)}{2 MB }}$ .......(1) When polarity of one magnet is reversed, M’ = M $\sim$ 2M = M; so $T ^{\prime}=2 \pi \sqrt{\frac{\left( I _{1}+ I _{2}\right)}{ MB }}$ .......(2) Dividing $${\rm{e}}{{\rm{q}}^n}$$ (2) by (1), $\frac{T^{\prime}}{T}=\sqrt{3}$ i.e., $T ^{\prime}=(\sqrt{3}) T =3 \sqrt{3} sec$
Ex. A circular coil of 16 turns and radius 10 cm, carrying a current of 0.75 A rests with its plane normal to an external field of magnitude $5.0 \times 10^{-2} T$ The coil is free to turn about an axis in its plane perpendicular to the field direction. When the coil is turned slightly and released, it oscillated about its stable equilibrium with a frequency of $2.0 s ^{-1}$ What is the moment of inertia of the coil about its axis of rotation? Sol. Here, $\mathrm{N}=16, \quad \mathrm{r}=10 \mathrm{cm}=0.1 \mathrm{m}$ i.e., $\quad A=\pi(0.1)^{2}$ $\mathrm{I}=0.75 \mathrm{A}_{\max } B=5.0 \times 10^{-2} T \quad v=2 s^{-1} \quad$ i.e., $\quad \mathrm{T}=0.5 \mathrm{sec}$ magnetic moment of coil $\quad M=N A I=16 \times \pi(0.1)^{2} \times 0.75=0.3768 A m^{2}$ $T=2 \pi \sqrt{\frac{I}{M B}} \quad(\mathrm{I}=$ Moment of inertia of the coil) $I=\frac{T^{2} M B}{4 \pi^{2}}=\frac{0.5 \times 0.5 \times 0.3768 \times 5.0 \times 10^{-2}}{4 \times 3.14 \times 3.14}=\frac{5 \times 5 \times 3768 \times 5}{4 \times 314 \times 314} \times 10^{-4}=1.1943 \times 10^{-4} \mathrm{kg}-m^{2}$
Also Read: Biot Savart's Law Click here for the Video tutorials of Magnetic Effect of Current Class 12
About eSaral At eSaral we are offering a complete platform for IIT-JEE & NEET preparation. The main mission behind eSaral is to provide education to each and every student in India by eliminating the Geographic and Economic factors, as a nation’s progress and development depends on the availability of quality education to each and every one. With the blend of education & technology, eSaral team made the learning personalized & adaptive for everyone.For free video lectures and complete study material, Download eSaral APP.
