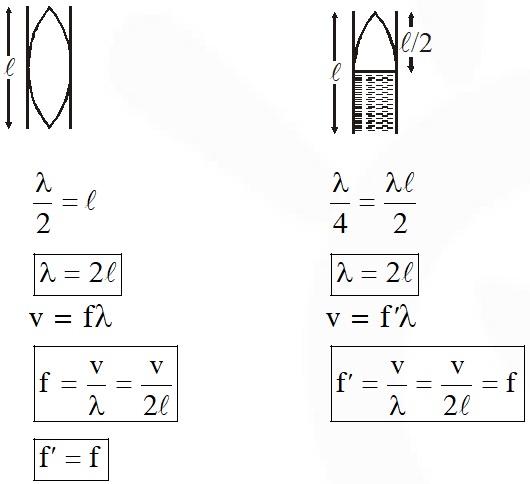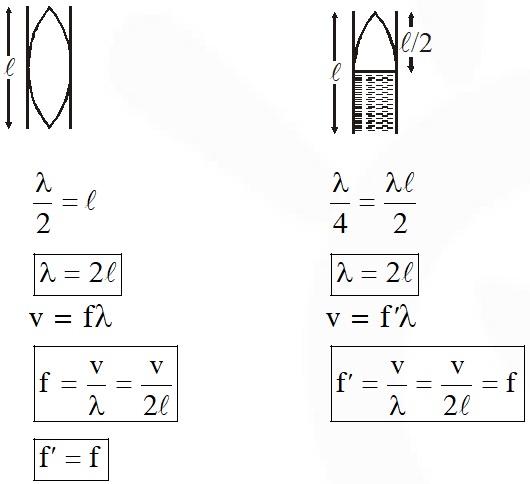JEE Main Previous Year Question of Physics with Solutions are available here. Practicing JEE Main Previous Year Papers Questions of Physics will help all the JEE aspirants in realizing the question pattern as well as help in analyzing their weak & strong areas.
Get detailed Class 11th &12th Physics Notes to prepare for Boards as well as competitive exams like IIT JEE, NEET etc.
eSaral helps the students in clearing and understanding each topic in a better way. eSaral is providing complete chapter-wise notes of Class 11th and 12th both for all subjects.
Besides this, eSaral also offers NCERT Solutions, Previous year questions for JEE Main and Advance, Practice questions, Test Series for JEE Main, JEE Advanced and NEET, Important questions of Physics, Chemistry, Math, and Biology and many more.
Download eSaral app for free study material and video tutorials.
Simulator
Previous Years AIEEE/JEE Mains Question
Q. The equation of a wave on a string of linear mass density 0.04 kg $\mathrm{m}^{-1}$ is given by y $=0.02(\mathrm{m}) \sin \left[2 \pi\left(\frac{\mathrm{t}}{0.04(\mathrm{s})}-\frac{\mathrm{x}}{0.50(\mathrm{m})}\right)\right]$. The tension in the string is :
(1) 6.25 N (2) 4.0 N (3) 12.5 N (4) 0.5 N
[AIEEE - 2010]
Ans. (1)
$y=0.2 \sin \left[2 \pi\left(\frac{t}{0.04}-\frac{x}{0.50}\right)\right]$
$\mathrm{v}=\sqrt{\frac{\mathrm{T}}{\mathrm{m}}}=\frac{\omega}{\mathrm{k}} \Rightarrow \sqrt{\frac{\mathrm{T}}{0.04}}=\frac{\frac{1}{0.04}}{\frac{1}{0.50}}$
$\mathrm{T}=\left(\frac{0.50}{0.04}\right)^{2} \times 0.04=6.25 \mathrm{N}$
Q. The transverse displacement y(x, t) of a wave on a string is given by $y(\mathrm{x}, \mathrm{t})=e^{-\left(\mathrm{ax}^{2}+\mathrm{bt}^{2}+2 \sqrt{\mathrm{ab}} \mathrm{xt}\right)}$. This represents a :-
(1) standing wave of frequency $\sqrt{b}$
(2) standing wave of frequency $\frac{1}{\sqrt{\mathrm{b}}}$
(3) wave moving in $+x$ directionwith speed $\sqrt{\frac{a}{b}}$
(4) wave moving in -x direction with speed $\sqrt{\frac{b}{a}}$
[AIEEE - 2011]
Ans. (4)
$y\left(x_{1} t\right)=e^{-[\sqrt{a x}+\sqrt{b t}]^{2}}$
$\mathrm{v}=\omega / \mathrm{K}=\frac{\sqrt{\mathrm{b}}}{\sqrt{\mathrm{a}}}$ in -ve $\mathrm{x}$ direction.
Q. Statement-1: Two longitudinal waves given by equations : $\mathrm{y}_{1}(\mathrm{x}, \mathrm{t})=2 \mathrm{a} \sin (\omega \mathrm{t}-\mathrm{kx})$ and $\mathrm{y}_{2}$ (x, t) = a sin (2$\omega$t – 2kx) will have equal intensity.
Statement-1: Intensity of waves of given frequency in same medium is proportional to square of amplitude only.
(1) Statement-1 is false, statement-2 is true
(2) Statement-1 is ture, statement-2 is false
(3) Statement-1 is ture, statement-2 true; statement-2 is the correct explanation of statement-1
(4) Statement-1 is true, statement-2 is true; statement -2 is not correct explanation of statement-1.
[AIEEE - 2011]
Ans. (2)
$\mathrm{y}_{1}(\mathrm{x}, \mathrm{t})=2 \mathrm{a} \sin (\mathrm{wt}-\mathrm{kx})$
$y_{2}(\mathrm{x}, \mathrm{t})=\mathrm{a} \sin (2 \mathrm{wt}-2 \mathrm{kx})$
But Intensity
$\mathrm{I}=2 \pi^{2} n^{2} \mathrm{a}^{2} \rho \mathrm{v} \Rightarrow \frac{\mathrm{I}_{1}}{\mathrm{I}_{2}}=\left(\frac{2 \mathrm{a}}{\mathrm{a}} \times \frac{\mathrm{n}}{2 \mathrm{n}}\right)^{2}=\frac{1}{1}$
Intensity depends on frequency and amplitude
So statement- 1 is true statement- 2 is false
Q. A travelling wave represented by y = A sin($\omega$t–kx) is superimposed on another wave represented by y = A sin ($\omega$t + kx). The resultant is :-
(1) A standing wave having nodes at $x=\left(n+\frac{1}{2}\right) \frac{\lambda}{2}, n=0,1,2$
(2) A wave travelling along $+x$ direction
(3) A wave travelling along - x direction
(4) A standing wave having nodes at $\mathrm{x}=\frac{\mathrm{n} \lambda}{2} ; \mathrm{n}=0,1,2$
[AIEEE-2011]
Ans. (1)
$y_{1}=A \sin (w t-k x) \& y_{2}=A \sin (w t+k x)$
By superposition principle
$y=y_{1}+y_{2}$
$=A \sin (w t-k x)+A \sin (w t+k x)$
$=2 \mathrm{A} \sin \mathrm{wt} \cos \mathrm{kx}$
Amplitude = 2A cos kx
At nodes displacement is minimum
$2 \mathrm{A} \cos \mathrm{kx}=0 \Rightarrow \cos \mathrm{kx}=0$
$\mathrm{kx}=(2 \mathrm{n}+1) \frac{\pi}{2} \Rightarrow \frac{2 \pi}{2} \mathrm{x}=(2 \mathrm{n}+1) \frac{\pi}{2}$
$\mathrm{x}=(2 \mathrm{n}+1) \frac{\pi}{4}$ where $\mathrm{n}=0,1,2 \ldots$
Q. A sonometer wire of length 1.5m is made of steel. The tension in it produces an elastic strain of 1%. What is the fundamental frequency of steel if density and elasticity of steel are 7.7 × $10^{3}$ $\mathrm{kg} / \mathrm{m}^{3}$ and 2.2 × $10^{11} \mathrm{N} / \mathrm{m}^{2}$ respectively ?
(1) 188.5 Hz (2) 178.2 Hz (3) 200.5 Hz (4) 770 Hz
[JEE-Main-2013]
Ans. (2)
Fundamental frequency
$\mathrm{f}=\frac{\mathrm{V}}{2 \ell}=\frac{1}{2 \times 1.5} \sqrt{\frac{\mathrm{T}}{\mathrm{eq}}}=\frac{1}{3} \sqrt{\frac{\mathrm{y} \times \operatorname{strain} \times \mathrm{S}}{\rho \mathrm{S}}}$
(S cross – section Area)
$=\frac{1}{3} \sqrt{\frac{2.2 \times 10^{11} \times \frac{1}{100}}{7.7 \times 10^{3}}}=178.2 \mathrm{Hz}$
Q. A uniform string of length 20m is suspended from a rigid support. A short wave pulse is introduced at its lowest end. It starts moving up the string. The time taken to reach the support is :-
(take $\left.\mathrm{g}=10 \mathrm{ms}^{-2}\right)$
(1) $\sqrt{2} \mathrm{s}$
(2) $2 \pi \sqrt{2} \mathrm{s}$
(3) 2s
(4) $2 \sqrt{2} \mathrm{s}$
[JEE-Main-2016]
Ans. (4)
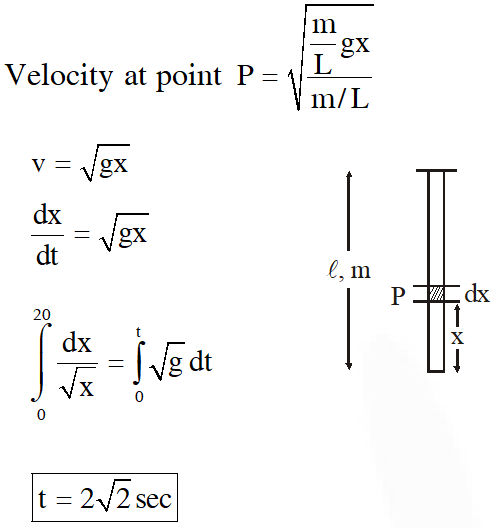
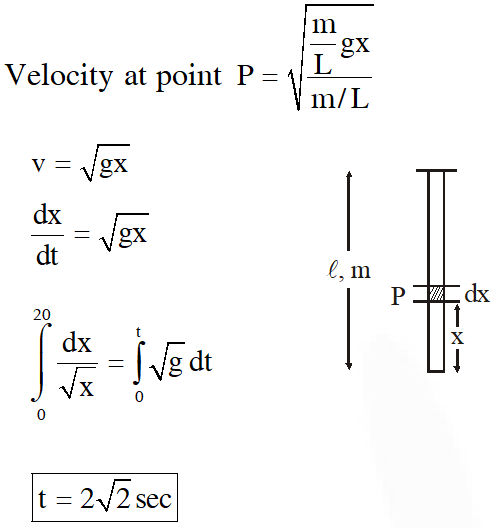
Q. A pipe open at both ends has a fundamental frequency f in air. The pipe is dipped vertically in water so that half of it is in water. The fundamental frequencty of the air column is now :-
(1) f
(2) $\frac{\mathrm{f}}{2}$
(3) $\frac{3 \mathrm{f}}{4}$
(4) 2f
[JEE-Main-2016]
Ans. (1)