JEE Advanced Previous Year Questions of Physics with Solutions are available at eSaral. Practicing JEE Advanced Previous Year Papers Questions of Physics will help the JEE aspirants in realizing the question pattern as well as help in analyzing weak & strong areas.
Get detailed Class 11th & 12th Physics Notes to prepare for Boards as well as competitive exams like IIT JEE, NEET etc.
eSaral helps the students in clearing and understanding each topic in a better way. eSaral is providing complete chapter-wise notes of Class 11th and 12th both for all subjects.
Click Here for JEE main Previous Year Topic Wise Questions of Physics with Solutions
Download eSaral app for free study material and video tutorials.
Simulator
Previous Years JEE Advanced Questions
Q. Column I shows four situations of standard Young’s double slit arrangement with the screen placed far away from the slits $S_{1}$ and $S_{2}$. In each of these cases $S_{1} P_{0}$ = $S_{2} P_{0}$, $S_{1} P_{1}$ – $S_{2} P_{1}$ = $\lambda / 4$ and $S_{1} P_{2}$ – $S_{2} P_{2}=\lambda / 3$, where $\lambda$ is the wavelength of the light used. In the cases B, C and D, a transparent sheet of refractive index $\mu$ and thickness t is pasted on slit S2. The thicknesses of the sheets are different in different cases. The phase difference between the light waves reaching a point P on the screen from the two slits is denoted by $\delta$ (P) and the intensity by I(P). Match each situation given in Column I with the statement(s) in Column II valid for that situation.
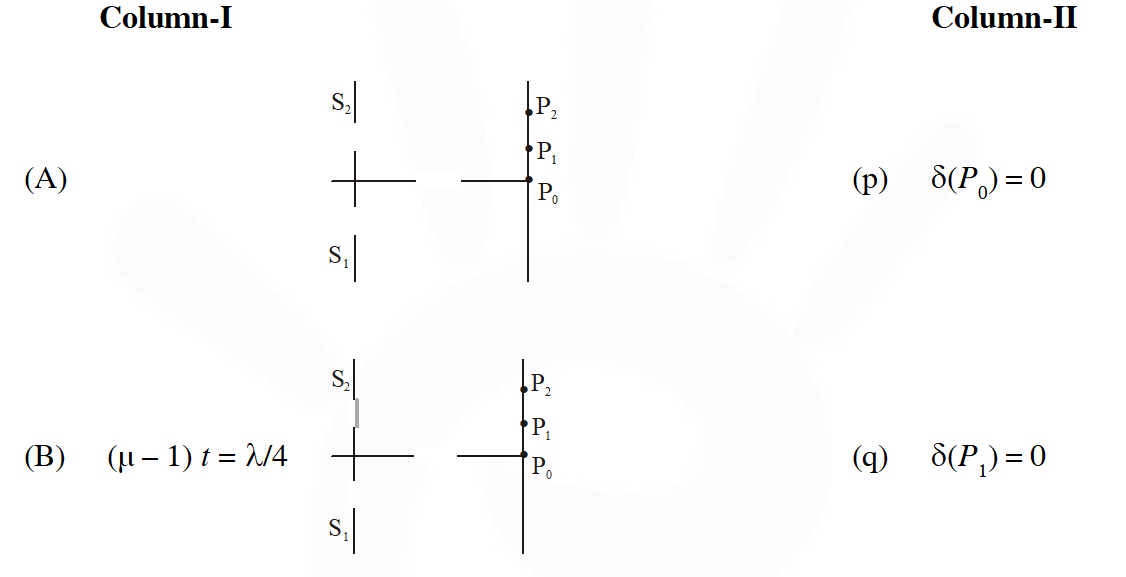
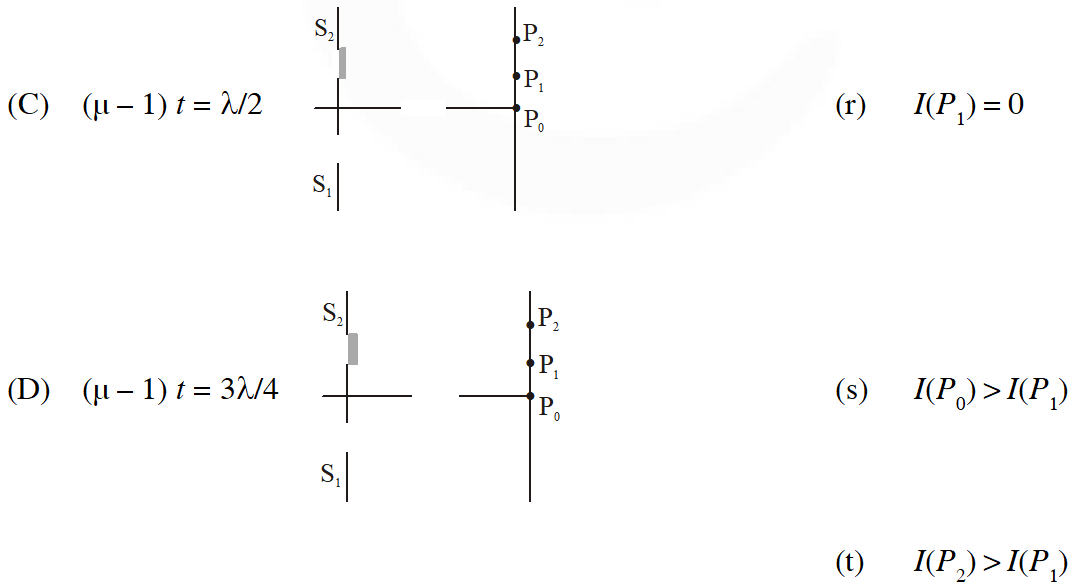[IIT-JEE-2009]
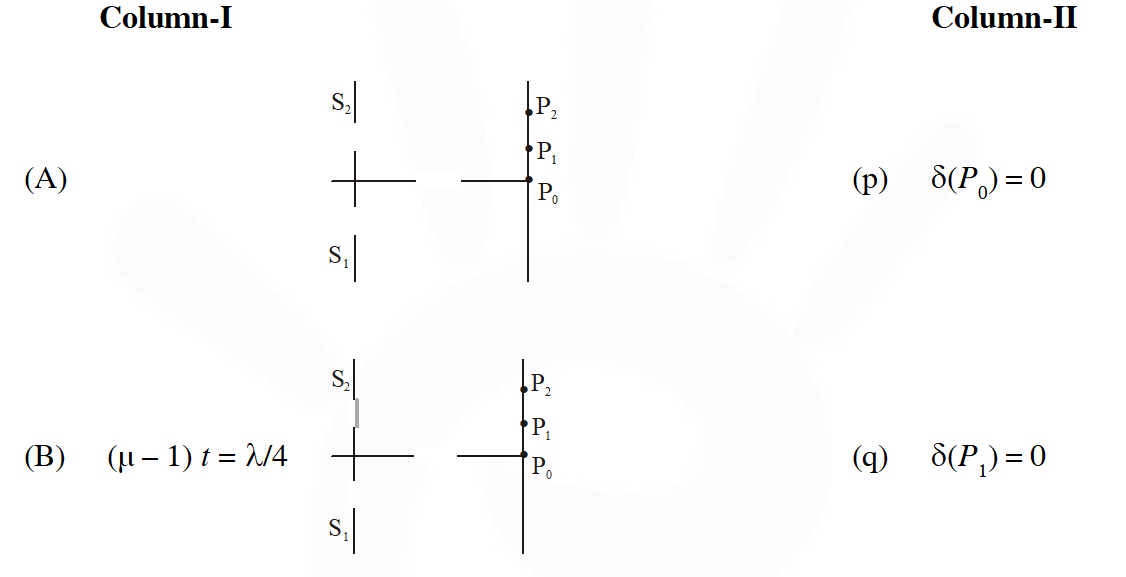
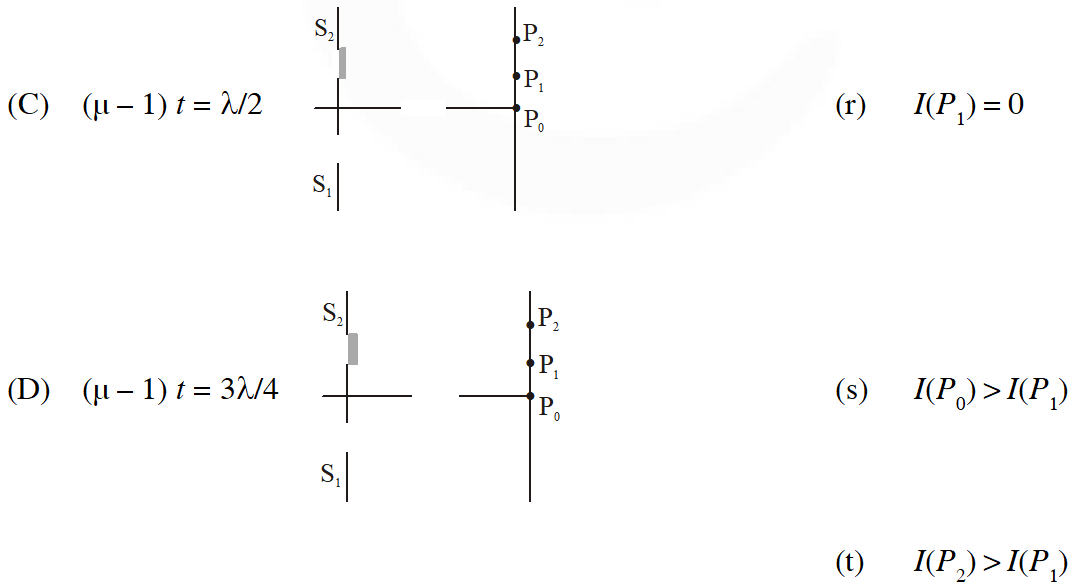[IIT-JEE-2009]
Ans. ((A) $p, s ;(B) q ;(C) t ;(D) r, s, t$)
(A) $\Delta \mathrm{x}=\mathrm{S}_{2} \mathrm{P}-\mathrm{S}_{1} \mathrm{P}=0$
$\delta\left(\mathrm{P}_{0}\right)=\frac{2 \pi}{\lambda} \Delta \mathrm{x}=0$
$\Delta \mathrm{x}=\mathrm{S}_{1} \mathrm{P}_{1}-\mathrm{S}_{2} \mathrm{P}_{1}=\frac{\lambda}{4}$
$\delta\left(\mathrm{P}_{1}\right)=\frac{2 \pi}{\lambda} \times \frac{\lambda}{4}=\frac{\pi}{2}$
$\mathrm{I}=\mathrm{I}_{\max } \cos ^{2}\left(\frac{\Delta \phi}{2}\right)$
$\mathrm{I}\left(\mathrm{P}_{1}\right)=\mathrm{I}_{1}=\mathrm{I}_{\max } \cos ^{2} \frac{\delta}{2}=\frac{\mathrm{I}_{\max }}{2}$
$\delta\left(\mathrm{P}_{2}\right)=\frac{2 \pi}{\lambda} \times \frac{\lambda}{3}=\frac{2 \pi}{3}$
$\mathrm{I}\left(\mathrm{P}_{2}\right)=\mathrm{I}_{2}=\mathrm{I}_{\max } \cos ^{2} \frac{\pi}{3}=\frac{\mathrm{I}_{\max }}{4}$
$\mathrm{I}\left(\mathrm{P}_{0}\right)>\mathrm{I}\left(\mathrm{P}_{1}\right)$
$(\mathrm{B}) \Delta \mathrm{x}=\mathrm{S}_{1} \mathrm{P}-\left[\mathrm{S}_{2} \mathrm{P}+(\mu-1) \mathrm{t}\right]$
$\Delta \mathrm{x}_{1}=\mathrm{S}_{1} \mathrm{P}_{1}-\mathrm{S}_{2} \mathrm{P}_{1}-(\mu-1) \mathrm{t}$
$\Delta \mathrm{x}_{1}=\frac{\lambda}{4}-\frac{\lambda}{4}=0$
$8\left(\mathrm{P}_{1}\right)=0 ; \mathrm{I}\left(\mathrm{P}_{1}\right)=\mathrm{I}_{\max }$
$8\left(\mathrm{P}_{0}\right)=\frac{\pi}{2} \delta\left(\mathrm{P}_{0}\right) \neq 0$
$\mathrm{I}\left(\mathrm{P}_{0}\right)=\mathrm{I}_{\max } / 2$
$\Delta \mathrm{x}=\mathrm{S}_{1} \mathrm{P}_{2}-\mathrm{S}_{1} \mathrm{P}_{2}-(\mu-1) \mathrm{t}$
$=\frac{\lambda}{3}-\frac{\lambda}{4}=\frac{\lambda}{12}$
$8\left(\mathrm{P}_{2}\right)=\frac{2 \pi}{\lambda} \times \frac{\lambda}{12}=\frac{\pi}{6}$
$\mathrm{I}\left(\mathrm{P}_{2}\right)=\mathrm{I}_{\max } \cos ^{2}\left(\frac{\pi}{12}\right)$
Q. Young's double slit experiment is carried out by using green, red and blue light, one color at a time. The fringe widths recorded are $\beta_{G}, \beta_{R}$ and $\beta_{B},$ respectively. Then
(A) $\beta_{G}>\beta_{B}>\beta_{R}$
(B) $\beta_{B}>\beta_{G}>\beta_{R}$
(C) $\beta_{R}>\beta_{B}>\beta_{G}$
(D) $\beta_{R}>\beta_{G}>\beta_{B}$
[IIT-JEE-2012]
Ans. (D)
$\beta=\frac{\mathrm{D} \lambda}{\mathrm{d}}$
$\lambda_{\mathrm{R}}>\lambda_{\mathrm{a}}>\lambda_{\mathrm{B}}$
Q. In the Young's double slit experiment using a monochromatic light of wavelength $\lambda$, the path difference (in terms of an integer n) corresponding to any point having half the peak intensity is :-
(A) $(2 n+1) \frac{\lambda}{2}$
(B) $(2 n+1) \frac{\lambda}{4}$
(C) $(2 n+1) \frac{\lambda}{8}$
$(D)(2 n+1) \frac{\lambda}{16}$
[JEE Advanced 2013]
Ans. (B)
$\frac{\mathrm{I}_{\max }}{2}=\mathrm{I}_{\max } \cos ^{2}\left(\frac{\pi}{\lambda} \Delta \mathrm{x}\right)$
$\cos ^{2}\left(\frac{\pi}{\lambda} \Delta \mathrm{x}\right)=\frac{1}{2}$
$\cos \left(\frac{\pi}{\lambda} \Delta \mathrm{x}\right)=\pm \frac{1}{\sqrt{2}}$
$\frac{\pi}{\lambda} \Delta \mathrm{x}=\mathrm{n} \pi \pm \frac{\pi}{4}$
$\Delta \mathrm{x}=\left(\mathrm{n} \pm \frac{1}{4}\right) \lambda$
Q. A light source, which emits two wavelengths $\lambda_{1}=400 \mathrm{nm}$ and $\lambda_{2}=600 \mathrm{nm},$ is used in a Young's double slit experiment. If recorded fringe widths for $\lambda_{1}$ and $\lambda_{2}$ are $\beta_{1}$ and $\beta_{2}$ and the number of fringes for them within a distance y on one side of the central maximum are $\mathrm{m}_{1}$ and $\mathrm{m}_{2},$ respectively, then :-
(A) $\beta_{2}>\beta_{1}$
(B) $\mathrm{m}_{1}>\mathrm{m}_{2}$
(C) From the central maximum, $3^{\mathrm{rd}}$ maximum of $\lambda_{2}$ overlaps with $5^{\text {th }}$ minimum of $\lambda_{1}$
(D) The angular separation of fringes of $\lambda_{1}$ is greater than $\lambda_{2}$
[JEE Advanced 2014]
Ans. (A,B,C)
$\beta=\frac{\mathrm{D} \lambda}{\mathrm{d}}$
$\mathrm{B}_{2}>\beta_{1}$
$\mathrm{y}=\mathrm{m}_{1} \frac{\mathrm{D} \lambda_{1}}{\mathrm{d}}=\mathrm{m}_{2} \frac{\mathrm{D} \lambda_{2}}{\mathrm{d}}$
$\frac{\mathrm{nD} \times \lambda_{2}}{\mathrm{d}}=\left(\mathrm{n}^{\prime}+\frac{1}{2}\right) \frac{\mathrm{D} \lambda_{1}}{\mathrm{d}} \Rightarrow 600 \mathrm{n}=\left(\mathrm{n}^{\prime}+\frac{1}{2}\right) \times 4$
Q. A Young's double slit interference arrangement with slits $S_{1}$ and $S_{2}$ is immersed in water (refractive index $=4 / 3$ ) as shown in the figure. The positions of maxima on the surface of water are given by $x^{2}=p^{2} m^{2} \lambda^{2}-d^{2},$ where $\lambda$ is the wavelength of light in air (refractive index $=1$, $2 d$ is the separation between the slits and $m$ is an integer. The value of p is.
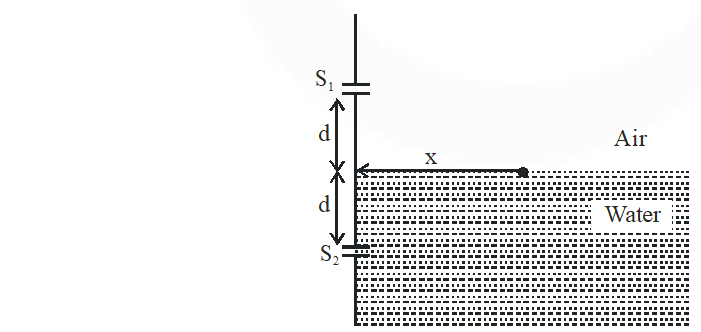[JEE Advanced 2015]
[JEE Advanced 2015]
Ans. 3
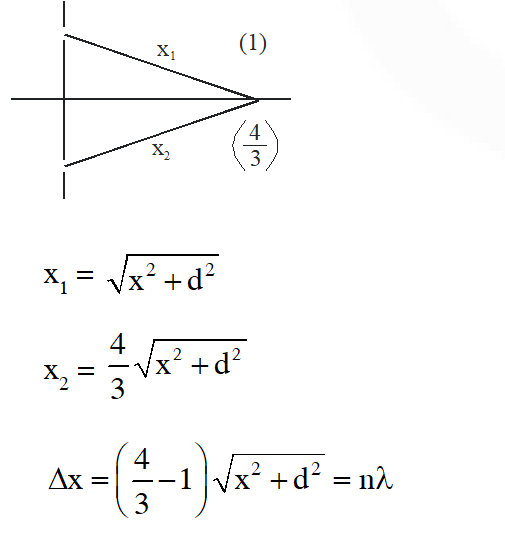
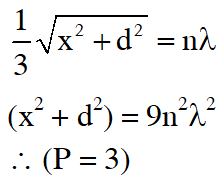
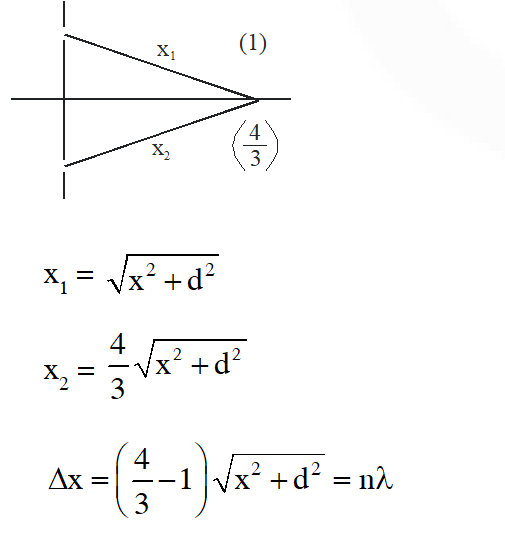
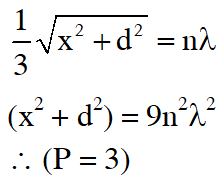
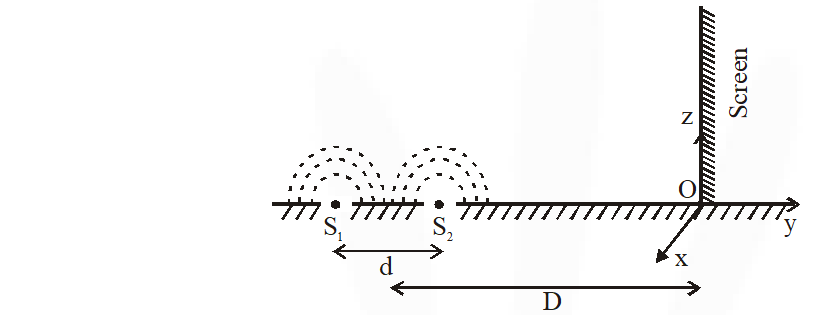
Q. While conducting the Young's double slit experiment, a student replaced the two slits with a large opaque plate in the x-y plane containing two small holes that act as two coherent point sources $\left(\mathrm{S}_{1}, \mathrm{S}_{2}\right)$ emitting light of wavelength 600 nm. The student mistakenly placed the screen parallel to the x-z plane (for z > 0) at a distance D = 3m from the mid-point of $\mathrm{S}_{1} \mathrm{S}_{2}$, as shown schematically in the figure. The distance between the sources d = 0.6003 mm. The origin O is at the intersection of the screen and the line joining $\mathrm{S}_{1} \mathrm{S}_{2}$. Which of the following is (are) true of the intensity pattern on the screen ?
(A) Hyperbolic bright and dark bands with foci symmetrically placed about O in the x-direction
(B) Semi circular bright and dark bands centered at point O
(C) The region very close to the point O will be dark
(D) Straight bright and dark bands parallel to the x-axis
[JEE-Mains 2016]
[JEE-Mains 2016]
Ans. (B,C)
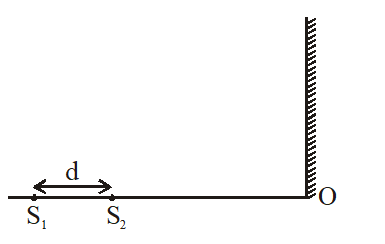Path difference at point O = d = .6003 mm = 600300 nm
$=\frac{2001}{2}(600 \mathrm{nm})=1000 \lambda+\frac{\lambda}{2}$
$\Rightarrow$ minima form at point $\mathrm{O}$
Line $S_{1} S_{2}$ and screen are $\perp$ to each other so fringe pattern is circular (semi-circular because only half of screen is available)
Path difference at point O = d = .6003 mm = 600300 nm
$=\frac{2001}{2}(600 \mathrm{nm})=1000 \lambda+\frac{\lambda}{2}$
$\Rightarrow$ minima form at point $\mathrm{O}$
Line $S_{1} S_{2}$ and screen are $\perp$ to each other so fringe pattern is circular (semi-circular because only half of screen is available)
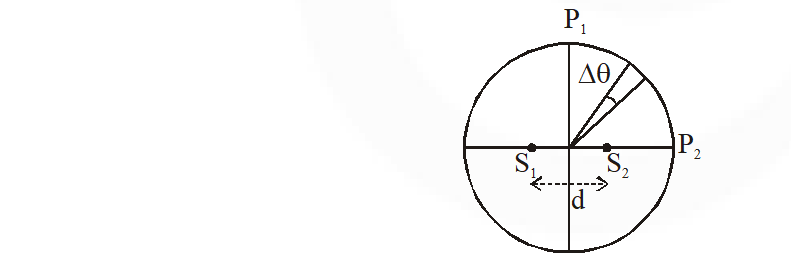
Q. Two coherent monochromatic point sources $\mathrm{S}_{1}$ and $\mathrm{S}_{2}$ of wavelength $\lambda$ = 600 nm are placed symmetrically on either side of the center of the circle as shown. The sources are separated by a distance d = 1.8mm. This arrangement produces interference fringes visible as alternate bright and dark spots on the circumference of the circle. The angular separation between two consecutive bright spots is $\Delta \theta$. Which of the following options is/are correct ?
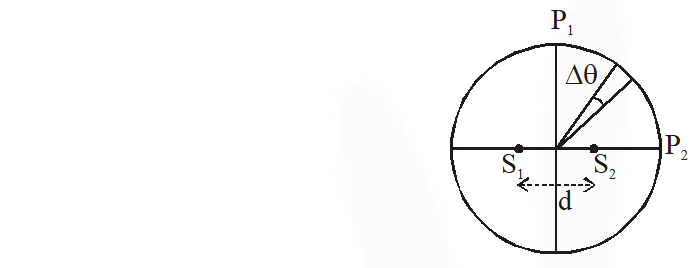(A) A dark spot will be formed at the point $\mathrm{P}_{2}$
(B) The angular separation between two consecutive bright spots decreases as we move from $\mathrm{P}_{1}$ to $\mathrm{P}_{2}$ along the first quadrant
(C) At $\mathrm{P}_{2}$ the order of the fringe will be maximum
(D) The total number of fringes produced between $P_{1}$ and $\mathrm{P}_{2}$ in the first quadrant is close to 3000
[JEE Advanced 2017]
(A) A dark spot will be formed at the point $\mathrm{P}_{2}$
(B) The angular separation between two consecutive bright spots decreases as we move from $\mathrm{P}_{1}$ to $\mathrm{P}_{2}$ along the first quadrant
(C) At $\mathrm{P}_{2}$ the order of the fringe will be maximum
(D) The total number of fringes produced between $P_{1}$ and $\mathrm{P}_{2}$ in the first quadrant is close to 3000
[JEE Advanced 2017]
Ans. (C,D)
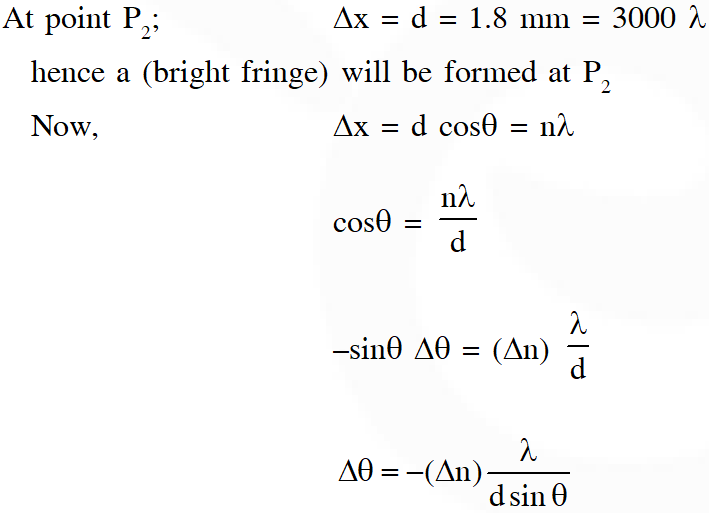
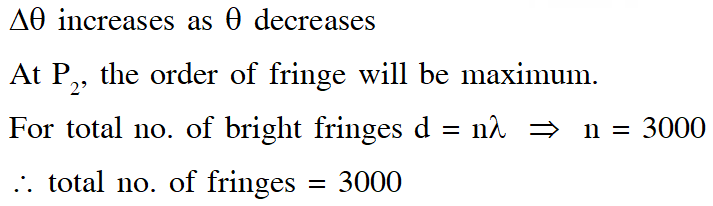
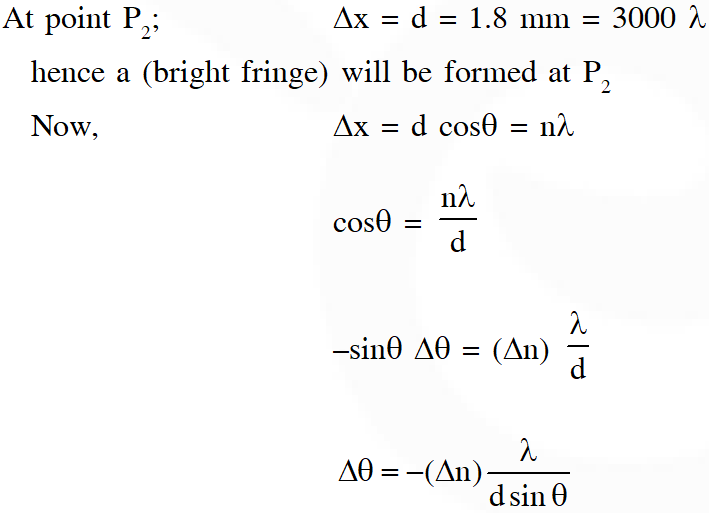
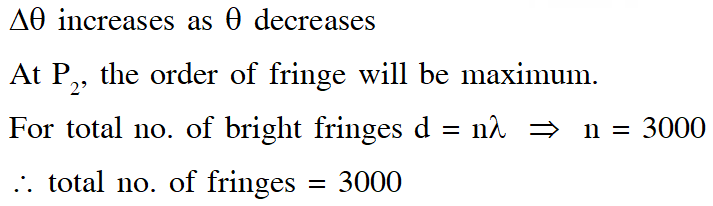
Comments
bekar website hai
Jan. 9, 2021, 5:19 p.m.
gandu kahika chutiya kahika saaala click lock karke lrakha hai. gaand mai ghusale website.
Ritik Ranjan
Nov. 6, 2020, 9:34 a.m.
that matching was literally thought provoking...i liked that question..
i think solving that question without pen is better