JEE Main Previous Year Question of Physics with Solutions are available here. Practicing JEE Main Previous Year Papers Questions of Physics will help all the JEE aspirants in realizing the question pattern as well as help in analyzing their weak & strong areas.
Get detailed Class 11th &12th Physics Notes to prepare for Boards as well as competitive exams like IIT JEE, NEET etc.
eSaral helps the students in clearing and understanding each topic in a better way. eSaral is providing complete chapter-wise notes of Class 11th and 12th both for all subjects.
Besides this, eSaral also offers NCERT Solutions, Previous year questions for JEE Main and Advance, Practice questions, Test Series for JEE Main, JEE Advanced and NEET, Important questions of Physics, Chemistry, Math, and Biology and many more.
Download eSaral app for free study material and video tutorials.
Simulator
Previous Years AIEEE/JEE Mains Questions
Direction : Questions number 3 to 5 are based on the following paragraph.
An initially parallel cylindrical beam travels in a medium of refractive index $\mu(\mathrm{I})=\mu_{0}+\mu_{2} \mathrm{I}$, where $\mu_{0}$ and $\mu_{2}$ are positive constants and I is the intensity of the light beam. The intensity of the beam is decreasing with increasing radius.
Q. A mixture of light, consisting of wavelength 590 nm and an unknown wavelength, illuminates Young's double slit and gives rise to two overlapping interference patterns on the screen. The central maximum of both lights coincide. Further, it is observed that the third bright fringe of known light coincides with the 4th bright fringe of the unknown light. From this data, the wavelength of the unknown light is :-
(1) 442.5 nm (2) 776.8 nm (3) 393.4 nm (4) 885.0 nm
[AIEEE-2009]
Ans. (1)
$\frac{3 \mathrm{D} \lambda_{1}}{\mathrm{d}}=\frac{4 \mathrm{D} \lambda_{2}}{\mathrm{d}}$
Q. The initial shape of the wavefront of the beam is :-
(1) planar
(2) convex
(3) concave
(4) convex near the axis and concave near the periphery
[AIEEE-2010]
Ans. (1)
For a parallel beam wavefronts are plane wave fronts.
Q. The speed of the light in the medium is :-
(1) maximum on the axis of the beam
(2) minimum on the axis of the beam
(3) the same everywhere in the beam
(4) directly proportional to the intensity I
[AIEEE-2010]
Ans. (2)
Intensity is maximum at the axis of the cylindrical beam. Hence $\mu$ is maximum at the axis due to
the relation $\mu=\mu_{0}+\mu_{2} \mathrm{I}$
Q. As the beam enters the medium, it will :-
(1) travel as a cylindrical beam
(2) diverge
(3) converge
(4) diverge near the axis and converge near the periphery
[AIEEE-2010]
Ans. (3)
v is minimum at the axis of beam. Hence beam will converge.
Q. At two points P and Q on screen in Young's double slit experiment, waves from slits $\mathrm{S}_{1}$ and $\mathrm{S}_{2}$ have a path difference of 0 and respectively. the ratio of intensities at P and Q will be :
(1) 3 : 2 (2) 2 : 1 (3) $\sqrt{2}: 1$ (4) 4: 1
[AIEEE-2011]
Ans. (4)
$\mathrm{I}=\mathrm{I}_{\max } \cos ^{2}\left(\frac{\pi}{\lambda} \times \frac{\lambda}{4}\right)$
$\mathrm{I}=\mathrm{I}_{\max } \cos ^{2}\left(\frac{\pi}{4}\right)=\frac{1}{\sqrt{2}} \mathrm{I}_{\max }$
$\frac{\mathrm{I}_{\max }}{2}=\sqrt{2}$
Q. Statement-1: On viewing the clear blue portion of the sky through a Calcite Crystal, the intensity of transmitted light varies as the crystal is rotated.
Statement-1: The light coming from the sky is polarized due to scattering of sun light by particles in the atmosphere. The scattering is largest for blue light.
(1) Statement-1 is false, statement-2 is true
(2) Statement-1 is true, statement-2 is false
(3) Statement-1 is true, statement-2 true; statement-2 is the correct explanation of statement-1
(4) Statement-1 is true, statement-2 is true; statement -2 is not correct explanation of statement- 1.
[AIEEE-2011]
Ans. (3)
$\mathrm{I}=\mathrm{I}_{0} \cos ^{2} \theta ;$ Law of Malus
Q. In a Young's double slit experiment, the two slits act as coherent sources of waves of equal amplitude A and wavelength $\lambda$. In another experiment with the same arrangement the two slits are made to act as incoherent sources of waves of same amplitude and wavelength. If the intensity at the middle point of the screen in the first case is $I_{1}$ and in the second case $\mathrm{I}_{2}$, then the ratio is :-
(1) 4 (2) 2 3) 1 (4) 0.5
[AIEEE-2011]
Ans. (2)
$\mathrm{I}_{1}=4 \mathrm{I}_{0}$
$\mathrm{I}_{2}=2 \mathrm{I}_{0}$
$\frac{\mathrm{I}_{1}}{\mathrm{I}_{2}}=2$
Q. Direction : The question has a paragraph followed by two statement, Statement-1 and statement-2. Of the given four alternatives after the statements, choose the one that describes the statements.
A thin air film is formed by putting the convex surface of a plane-convex lens over a plane glass plate. With monochromatic light, this film gives an interference pattern due to light reflected from the top (convex) surface and the bottom (glass plate) surface of the film
Statement-1:
When light reflects from the air-glass plate interface, the reflected wave suffers a phase change of $\pi$.
Statement-2: The centre of the interference pattern is dark :-
(1) Statement-1 is true, Statement-2 is true and Statement-2 is not the correct explanation of
Statement-1.
(2) Statement-1 is false, Statement-2 is true
(3) Statement-1 is true, Statement-2 is false
(4) Statement-1 is true, Statement-2 is true and Statement-2 is the correct explanation of statement- 1.
[AIEEE-2011]
Ans. (1)
Q. In Young's double slit experiment, one of the slit is wider than other, so that the amplitude of the light from one slit is double of that from other slit. If $\mathbf{I}_{\mathrm{m}}$ be the maximum intensity, the resultant intensity I when they interfere at phase difference $\phi$ is given by :
[AIEEE-2012]
[AIEEE-2012]
Ans. (1)
$\mathrm{I}_{\mathrm{R}}=\mathrm{I}_{1}+\mathrm{I}_{2}+2 \sqrt{\mathrm{I}_{1} \mathrm{I}_{2}} \cos \Delta \phi$
$\mathrm{I}_{\mathrm{R}}=4 \mathrm{I}_{0}+\mathrm{I}_{0}+2 \times 2 \mathrm{I}_{0} \cos \phi$
$\mathrm{I}_{\mathrm{R}}=\mathrm{I}_{0}[5+4 \cos \phi]$
$\left(\mathrm{I}_{\mathrm{R}}\right)_{\max }=\mathrm{I}_{\mathrm{m}}=9 \mathrm{I}_{0}$
$\mathrm{I}_{\mathrm{R}}=\frac{\mathrm{I}_{\mathrm{m}}}{9}[1+4(1+\cos \phi)]$
$\mathrm{I}_{\mathrm{R}}=\frac{\mathrm{I}_{\mathrm{m}}}{9}\left[1+8 \cos ^{2} \frac{\phi}{2}\right]$
Q. This question has Statement-l and statement-2. Of the four choices given after the Statements, choose the one that best describes the two statements.
Statement-1 : Davisson - Germer experiment established the wave nature of electrons.
Statement-2: If electrons have wave nature, they can interfere and show diffraction.
(1) Statement-1 is true, Statement-2 is true and Statement-2 is the correct explanation for Statement-1.
(2) Statement-1 is true, Statement-2 is true and Statement-2 is not the correct explanation of
Statement-I
(3) Statement-1 is false, Statement-2 is true.
(4) Statement-1 is true, Statement-2 is false
[AIEEE - 2012]
Ans. (1)
Q. A beam of unpolarised light of intensity $\mathrm{I}_{0}$ is passed through a polaroid A and then through another polaroid B which is oriented so that its principal plane makes an angle of $45^{\circ}$ relative to that of A. The intensity of the emergent light is :-
( 1) $\mathrm{I}_{0}$ $(2) \mathrm{I}_{0} / 2$ (3) $\mathrm{I}_{0} / 4$ (4) $\mathrm{I}_{0} / 8$
[JEE-Mains 2013]
Ans. (3)
$\mathrm{I}=\left(\frac{\mathrm{I}_{0}}{2}\right) \cos ^{2} 45^{\circ}$
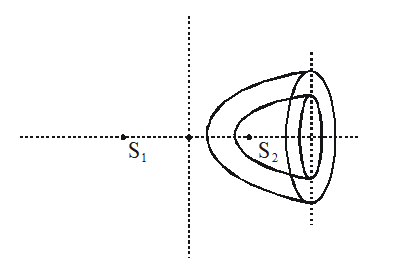
Q. Two coherent point sources $\mathrm{S}_{1}$ and $\mathrm{S}_{2}$ are separated by a small distance 'd' as shown. The fringes obtained on the screen will be :
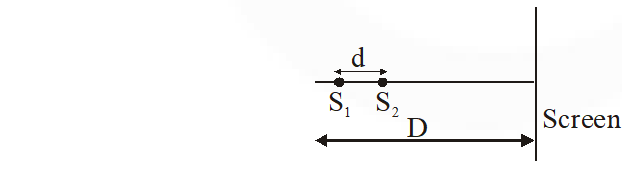(1) points (2) straight lines (3) semicircles (4) concentric circles
[JEE-Mains 2013]
(1) points (2) straight lines (3) semicircles (4) concentric circles
[JEE-Mains 2013]
Ans. (4)
Q. Two beams, A and B, of plane polarized light with mutually perpendicular planes of polarization are seen through a polaroid. From the position when the beam A has maximum intensity (and beam B has zero intensity), a rotation of polaroid through $30^{\circ}$ makes the two beams appear equally bright. If the initial intensitites of the two beams are $\mathrm{I}_{\mathrm{A}}$ and $\mathrm{I}_{\mathrm{B}}$ respectively, then $\frac{\mathrm{I}_{\mathrm{A}}}{\mathrm{I}_{\mathrm{B}}}$ equals :
(1) 1 (2) $\frac{1}{3}$ (3) 3 (4) $\frac{3}{2}$
[JEE-Main 2014]
Ans. (2)
When polaroid is at Angle $30^{\circ}$ with beam $\mathrm{A},$ it makes $60^{\circ}$ with beam $\mathrm{B}$
by malus law
$\mathrm{I}_{\mathrm{A}} \cos ^{2} 30^{\circ}=\mathrm{I}_{\mathrm{B}} \cos ^{2} 60^{\circ}$
$\Rightarrow \frac{\mathrm{I}_{\mathrm{A}}}{\mathrm{I}_{\mathrm{B}}}=\frac{1}{3}$
Q. Assuming human pupil to have a radius of 0.25cm and a comfortable viewing distance of 25cm, the minimum separation between two objects that human eye can resolve at 500 nm wavelength is :-
(1) $100 \mu \mathrm{m}$
(2) $300 \mu \mathrm{m}$
(3) (3) $1 \mu m$
(4) $30 \mu \mathrm{m}$
[JEE-Mains 2015]
Ans. (4)
$\frac{\mathrm{d}_{0}}{\mathrm{d}_{1}}=\theta=\frac{1.22 \lambda}{\mathrm{d}}$
$\mathrm{d}_{0}=\frac{1.22 \times 500 \times 10^{-9}}{0.5 \times 10^{-2}} \times 25 \times 10^{-2}$
$\mathrm{d}_{0}=1.22 \times 25 \times 10^{-6}$
$\mathrm{d}_{0} \square 30 \mu \mathrm{m}$
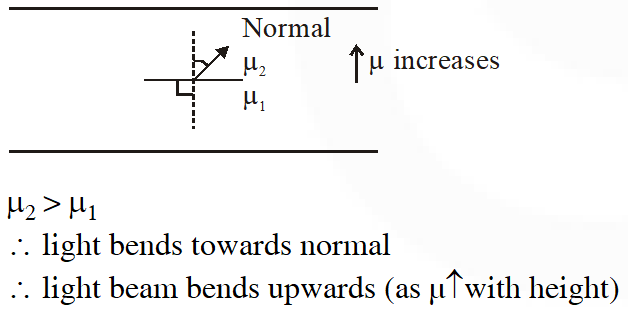
Q. On a hot summer night, the refractive index of air is smallest near the ground and increases with height from the ground. When a light beam is directed horizontally, the Huygens' principle leads us to conclude that as it travels, the light beam :
(1) bends downwards
(2) bends upwards
(3) becomes narrower
(4) goes horizontally without any deflection
[JEE-Mains 2015]
Ans. (2)
Q. The box of a pin hole camera, of length $L$, has a hole of radius a. It is assumed that when the holeis illuminated by a parallel beam of light of wavelength $\lambda$ the spread of the spot (obtained on theopposite wall of the camera) is the sum of its geometrical spread and the spread due to diffraction.The spot would then have its minimum size (say $b_{\min }$ ) when :-
(1) $\mathrm{a}=\frac{\lambda^{2}}{\mathrm{L}}$ and $\mathrm{b}_{\mathrm{min}}=\sqrt{4 \lambda \mathrm{L}}$
(2) $\mathrm{a}=\frac{\lambda^{2}}{\mathrm{L}}$ and $\mathrm{b}_{\min }=\left(\frac{2 \lambda^{2}}{\mathrm{L}}\right)$
(3) $\mathrm{a}=\sqrt{\lambda \mathrm{L}}$ and $\mathrm{b}_{\min }=\left(\frac{2 \lambda^{2}}{\mathrm{L}}\right)$
(4) $\mathrm{a}=\sqrt{\lambda \mathrm{L}}$ and $\mathrm{b}_{\min }=\sqrt{4 \lambda \mathrm{L}}$
[JEE-Mains 2016]
Ans. (4)
Spot size (diameter) $\mathrm{b}=2\left(\frac{\lambda \mathrm{L}}{2 \mathrm{a}}\right)+2 \mathrm{a}$
$\mathrm{a}^{2}+\lambda \mathrm{L}-\mathrm{ab}=0$
For Real roots $\mathrm{b}^{2}-4 \mathrm{L} \lambda \geq 0$
$\mathrm{b}_{\min .}=\sqrt{4 \lambda \mathrm{L}}$
by eq. ( i ) $\quad a=\sqrt{\lambda L}$
by eq. ( i ) $\quad a=\sqrt{\lambda L}$
Q. In a Young's double slit experiment, slits are separated by 0.5 mm, and the screen is placed 150 cm away. A beam of light consisting of two wavelengths, 650 nm and 520 nm, is used to obtain interference fringes on the screen. The least distance from the common central maximum to the point where the bright fringes due to both the wavelengths coincide is :-
(1) 9.75 mm (2) 15.6 mm (3) 1.56 mm (4) 7.8 mm
[JEE-Mains 2017]
Ans. (4)
For common maxima
$\mathrm{n}_{1} \lambda_{1}=\mathrm{n}_{2} \lambda_{2}$
$\mathrm{n}_{1} \times 650=\mathrm{n}_{2} \times 520$
$\frac{\mathrm{n}_{1}}{\mathrm{n}_{2}}=\frac{4}{5}$
$\frac{\mathrm{n}_{1}}{\mathrm{D}_{2}}=\mathrm{n} \lambda$
$\frac{\mathrm{yd}}{\mathrm{D}}=\mathrm{n} \lambda$
$\mathrm{y}=\frac{4 \times 650 \times 10^{-9} \times 1.5}{0.5 \times 10^{-3}}$
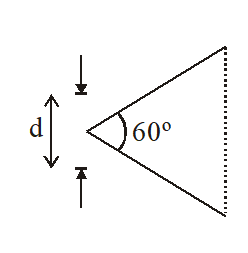
Q. The angular width of the central maximum in a single slit diffraction pattern is $60^{\circ}$ . The width of the slit is 1 m. The slit is illuminated by monochromatic plane waves. If another slit of same width is made near it, Young’s fringes can be observed on a screen placed at a distance
50 cm from the slits. If the observed fringe width is 1 cm, what is slit separation distance? (i.e. distance between the centres of each slit.)
(1) $50 \mu \mathrm{m}$
(2) $75 \mu \mathrm{m}$
(3) $100 \mu \mathrm{m}$
(4) $25 \mu \mathrm{m}$
[JEE-Mains 2018]
Ans. (4)
In diffraction
d $\sin 30^{\circ}=\lambda$
$\lambda=\frac{\mathrm{d}}{2}$
Young's fringe width
[d'- separation between two slits]
$$
\beta=\frac{\lambda \times \mathrm{D}}{\mathrm{d}^{\prime}}
$$
$10^{-2}=\frac{\mathrm{d}}{2} \times \frac{50 \times 10^{-2}}{\mathrm{d}}$
$10^{-2}=\frac{10^{-6} \times 50 \times 10^{-2}}{2 \times \mathrm{d}^{\prime}}$
$\mathrm{d}^{\prime}=25 \mu \mathrm{m}$
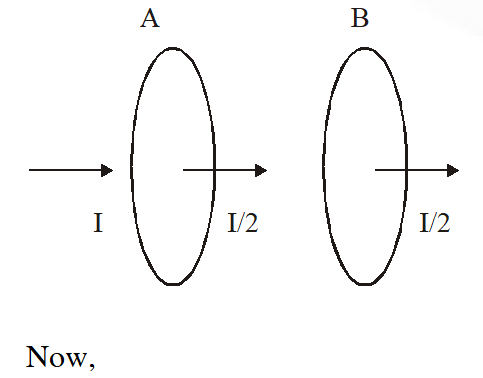
Q. Unpolarized light of intensity I passes through an ideal polarizer A. Another identical polarizer B is placed behind A. The intensity of light beyond B is found to be $\frac{1}{2}$. Now another identical polarizer C is placed between A and B. The intensity beyond B is now found to be $\frac{\mathrm{I}}{8}$. The angle between polarizer A and C is :
(1) $30^{\circ}$ ( 2) $45^{\circ}$ (3) $60^{\circ}$ (4) $0^{\circ}$
[JEE-Mains 2018]
Ans. (2)
Axis of transmission of A & B are parallel.
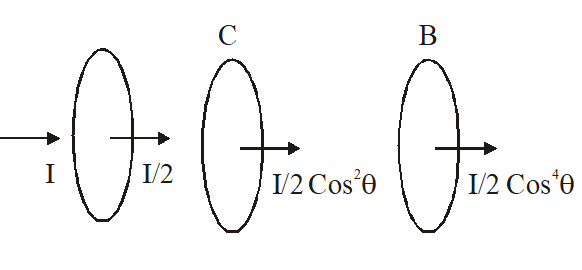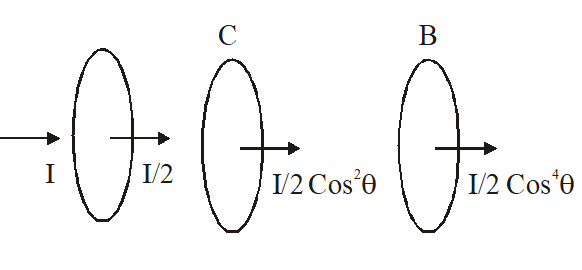$\frac{\mathrm{I}}{2} \cos ^{4} \theta=\frac{\mathrm{I}}{8} \Rightarrow \cos ^{4} \theta=\frac{1}{4}$
$\cos \theta=\frac{1}{\sqrt{2}}$
$\theta=45^{\circ}$
$\frac{\mathrm{I}}{2} \cos ^{4} \theta=\frac{\mathrm{I}}{8} \Rightarrow \cos ^{4} \theta=\frac{1}{4}$
$\cos \theta=\frac{1}{\sqrt{2}}$
$\theta=45^{\circ}$
Comments
D rugved
March 23, 2021, 10:27 a.m.
the level of questions are from moderate to tough and some are easy
thank you ......
Srikanth
Oct. 29, 2020, 3:05 p.m.
It is very useful, if some more explanation is there it will be useful
Hmm?
Aug. 30, 2020, 1:17 p.m.
Gand phatke hath me agayi. Exam ke pehele din parke pta nhi kya ukhad lunga