Hey, do you want to know what is capillarity in Physics? If yes. Then keep reading
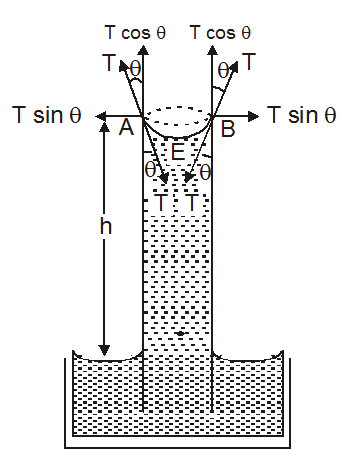Let a glass capillary tube of uniform bore be dipped vertically in a liquid that wets the glass. Such a liquid rises in the tube forming a concave meniscus as already discussed. since the force of surface tension tends to make the area of the free-surface minimum, it acts downwards along the tangent to the liquid meniscus at the point of contacts, such as E and F fig. This force of surface tension (i.e. action) acting all along the circle of contact pulls the tube downwards (inwards). An equal reaction to this force comes into play and acts on the liquid meniscus in the upward (outward) direction. The action is unable to pull downwards, as the tube is either held in hand or clamped. But the reaction remains unbalanced and hence pulls the liquid up. The liquid there goes on rising in the liquid up. The liquid therefore, goes on rising in the tube till the upward reaction is balanced by the weight of the liquid column raised.
Let,
r = radius of the capillary tube,
h = height to which the liquid rises as shown in the diagram,
d = density of the liquid at room temperature,
q = angle of contact between the liquid and the glass,
T = force of surface tension acting tangentially downward (inward) to the liquid meniscus.
R = reaction acting tangentially upwards (outwards) on the liquid meniscus.
Clearly, R = T
The reaction R can be resolved into two rectangular components.
The component $\mathrm{R} \cos \theta$ acts all along the circumference of the circle of contact of the liquid with the tube.
Circumference of the circle of contact $=2 \pi \mathrm{r}$
Since surface tension is the force acting per unit length,
Total upward force $=\mathrm{R} \cos \theta \times 2 \pi \mathrm{r}$
But
R = T
Total upward force $=T \cos \theta \times 2 \pi r$
Volume of the liquid in the cylindrical column of height h and radius $r=\pi r^{2} h$
If the tube is narrow, the radius of curvature of the meniscus is approximately equal to the radius (r) of the capillary tube.
Volume of the liquid under the meniscus = volume of the cylinder CDEF of height r and radius r – volume
of the hemisphere EFGE of radius
$r=\pi r^{2} \cdot r-\frac{1}{2} \times \frac{4}{3} \pi r^{3}$
$=\frac{1}{3} \pi r^{3}$
Total volume of the liquid in the capillary tube
$=\pi r^{2} . h+\frac{1}{3} \pi r^{3}$
$=(h+r / 3)$
Now, mass of liquid raised in the tube
m = volume $\times$ density
$=\pi r^{2}(h+r / 3) d$
Weight of liquid raised in the tube
$=m g=\pi r^{2}(h+r / 3) d . g$
This acts at C.G., the centre of gravity of liquid column in the tube.
In equilibrium, Total upward force = weight of liquid raised in the tube.
$\mathrm{T} \cos \theta \times 2 \pi \mathrm{r}$
$=\pi r^{2}(h+r / 3) d g$
Or
$h+\frac{r}{3}=\frac{2 T \cos \theta}{r d g}$
Or
$h=\frac{2 T \cos \theta}{r d g}-\frac{r}{3}$
Or
$\mathrm{T}=\frac{\mathrm{r}\left[\mathrm{h}+\left(\frac{\mathrm{r}}{3}\right)\right] \mathrm{dg}}{2 \cos \theta}$
This relation is known as ascent formula.
If the tube is very narrow, $\frac{r}{3}$ can be neglected in comparison with h, hence
$\mathrm{h}=\frac{2 \mathrm{~T} \cos \theta}{\mathrm{rdg}}$
Or
$\mathrm{T}=\frac{\mathrm{hrdg}}{2 \cos \theta}$
This is another form of ascent formula.
Jurien’s Law
Liquid raised at height h in a capillary tube is inversely proportional to the radius of the capillary tube.
Or
$h \propto \frac{1}{r}$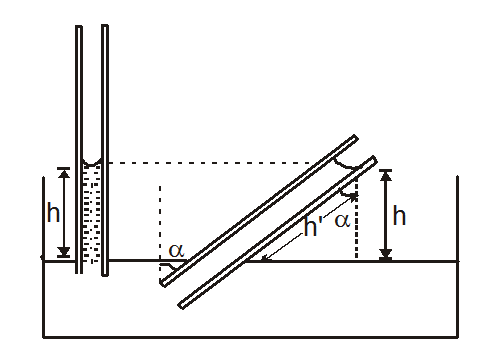
The height of liquid in capillary tube
$h=\frac{2 T \cos \theta}{r d g}$
Now, after inclination of capillary tube the liquid height remains unchange but the length of liquid becomes h’
Where
$h^{\prime}=\frac{h}{\cos \alpha}$
Or
$h^{\prime}=\frac{2 T \cos \theta}{r d g \cos \alpha}$
$\alpha=$ inclination of capillary tube with vertical.
(2) Capillarity in case of weightlessness:
If a capillary tube is dipped in water in case of weightlessness then the water will rise to the other end of the capillary tube and does not comes out because the shape of menicus balance it.
(3) If a capillary tube of insufficient length is dipped in a liquid then the liquid will not come out from the other end because the radius of curveture of menicus becomes large so it balances the surface tension.
(4) If a sphere of radius r has a hole and it is dipped at depth of h in a bikar field with the liquid. The depth h where the liquid does not rises in the hole is –
$h d g=\frac{2 T \cos \theta}{r}$
(5) To separate two glass plates which have a liquid film between them.
$\mathrm{F}=\frac{2 \mathrm{AT}}{\mathrm{t}}$
where A = surface area of contact of the plates.
t = distance between the plates.
(6) If the radius of the meniscus of a liquid is the same then in equilibrium the height h of the liquid remains the same in capillary tubes of different shapes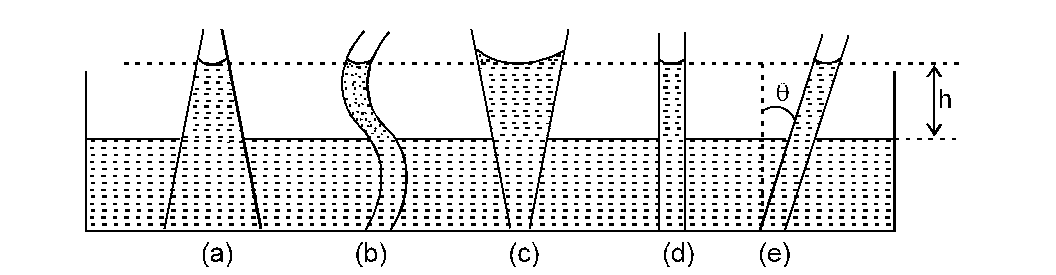
$\frac{\mathrm{h}_{1}}{\mathrm{~h}_{2}}=\frac{\mathrm{T}_{1}}{\mathrm{~T}_{2}} \times \frac{\mathrm{d}_{2}}{\mathrm{~d}_{1}}$
(other quantities cancel)
$=\frac{60}{50} \times \frac{0.6}{0.8}$
$=\frac{9}{10}$
$h_{1}: h_{2}=9: 10$
So, that's all from this Topic. I hope you get the idea about what is capillarity in Physics. If you have any confusion related to this topic please let us know in the comments section down below.
For a better understanding of this chapter, please check the detailed notes of Mechanical Properties of Fluids. If you want more Free Learning Videos and Study Material Then don't forget to download the eSaral App.
What is Capillarity
The rise and the fall of liquids in small cross-sectional area elements such as tubes known as capillarity. Tubes that have a very small diameter are known as Capillary.Capillarity
Let a glass capillary tube of uniform bore be dipped vertically in a liquid that wets the glass. Such a liquid rises in the tube forming a concave meniscus as already discussed. since the force of surface tension tends to make the area of the free-surface minimum, it acts downwards along the tangent to the liquid meniscus at the point of contacts, such as E and F fig. This force of surface tension (i.e. action) acting all along the circle of contact pulls the tube downwards (inwards). An equal reaction to this force comes into play and acts on the liquid meniscus in the upward (outward) direction. The action is unable to pull downwards, as the tube is either held in hand or clamped. But the reaction remains unbalanced and hence pulls the liquid up. The liquid there goes on rising in the liquid up. The liquid therefore, goes on rising in the tube till the upward reaction is balanced by the weight of the liquid column raised.
Let,
r = radius of the capillary tube,
h = height to which the liquid rises as shown in the diagram,
d = density of the liquid at room temperature,
q = angle of contact between the liquid and the glass,
T = force of surface tension acting tangentially downward (inward) to the liquid meniscus.
R = reaction acting tangentially upwards (outwards) on the liquid meniscus.
Clearly, R = T
The reaction R can be resolved into two rectangular components.
- $\mathrm{R} \cos \theta,$ acting upwards along the wall of the tube.
- $\mathrm{R} \sin \theta,$ acting perpendicular to the wall of the tube. This component, therefore, plays no part in raising the liquid in the tube
The component $\mathrm{R} \cos \theta$ acts all along the circumference of the circle of contact of the liquid with the tube.
Circumference of the circle of contact $=2 \pi \mathrm{r}$
Since surface tension is the force acting per unit length,
Total upward force $=\mathrm{R} \cos \theta \times 2 \pi \mathrm{r}$
But
R = T
Total upward force $=T \cos \theta \times 2 \pi r$
Volume of the liquid in the cylindrical column of height h and radius $r=\pi r^{2} h$
If the tube is narrow, the radius of curvature of the meniscus is approximately equal to the radius (r) of the capillary tube.
Volume of the liquid under the meniscus = volume of the cylinder CDEF of height r and radius r – volume
of the hemisphere EFGE of radius
$r=\pi r^{2} \cdot r-\frac{1}{2} \times \frac{4}{3} \pi r^{3}$
$=\frac{1}{3} \pi r^{3}$
Total volume of the liquid in the capillary tube
$=\pi r^{2} . h+\frac{1}{3} \pi r^{3}$
$=(h+r / 3)$
Now, mass of liquid raised in the tube
m = volume $\times$ density
$=\pi r^{2}(h+r / 3) d$
Weight of liquid raised in the tube
$=m g=\pi r^{2}(h+r / 3) d . g$
This acts at C.G., the centre of gravity of liquid column in the tube.
In equilibrium, Total upward force = weight of liquid raised in the tube.
$\mathrm{T} \cos \theta \times 2 \pi \mathrm{r}$
$=\pi r^{2}(h+r / 3) d g$
Or
$h+\frac{r}{3}=\frac{2 T \cos \theta}{r d g}$
Or
$h=\frac{2 T \cos \theta}{r d g}-\frac{r}{3}$
Or
$\mathrm{T}=\frac{\mathrm{r}\left[\mathrm{h}+\left(\frac{\mathrm{r}}{3}\right)\right] \mathrm{dg}}{2 \cos \theta}$
This relation is known as ascent formula.
If the tube is very narrow, $\frac{r}{3}$ can be neglected in comparison with h, hence
$\mathrm{h}=\frac{2 \mathrm{~T} \cos \theta}{\mathrm{rdg}}$
Or
$\mathrm{T}=\frac{\mathrm{hrdg}}{2 \cos \theta}$
This is another form of ascent formula.
Jurien’s Law
Liquid raised at height h in a capillary tube is inversely proportional to the radius of the capillary tube.
Or
$h \propto \frac{1}{r}$
Special points:
(1) If capillary tube is inclined then the effect on the height of the raised liquid.
The height of liquid in capillary tube
$h=\frac{2 T \cos \theta}{r d g}$
Now, after inclination of capillary tube the liquid height remains unchange but the length of liquid becomes h’
Where
$h^{\prime}=\frac{h}{\cos \alpha}$
Or
$h^{\prime}=\frac{2 T \cos \theta}{r d g \cos \alpha}$
$\alpha=$ inclination of capillary tube with vertical.
(2) Capillarity in case of weightlessness:
If a capillary tube is dipped in water in case of weightlessness then the water will rise to the other end of the capillary tube and does not comes out because the shape of menicus balance it.
(3) If a capillary tube of insufficient length is dipped in a liquid then the liquid will not come out from the other end because the radius of curveture of menicus becomes large so it balances the surface tension.
(4) If a sphere of radius r has a hole and it is dipped at depth of h in a bikar field with the liquid. The depth h where the liquid does not rises in the hole is –
$h d g=\frac{2 T \cos \theta}{r}$
(5) To separate two glass plates which have a liquid film between them.
$\mathrm{F}=\frac{2 \mathrm{AT}}{\mathrm{t}}$
where A = surface area of contact of the plates.
t = distance between the plates.
(6) If the radius of the meniscus of a liquid is the same then in equilibrium the height h of the liquid remains the same in capillary tubes of different shapes
Some applications of capillarity
- The rise of Kerosene in the wick in a Lantern.
- Sucking of ink by the blotting paper.
- The rise of ink in the nib of a fountain pen.
- Sucking of water by the towel.
$\frac{\mathrm{h}_{1}}{\mathrm{~h}_{2}}=\frac{\mathrm{T}_{1}}{\mathrm{~T}_{2}} \times \frac{\mathrm{d}_{2}}{\mathrm{~d}_{1}}$
(other quantities cancel)
$=\frac{60}{50} \times \frac{0.6}{0.8}$
$=\frac{9}{10}$
$h_{1}: h_{2}=9: 10$
So, that's all from this Topic. I hope you get the idea about what is capillarity in Physics. If you have any confusion related to this topic please let us know in the comments section down below.
For a better understanding of this chapter, please check the detailed notes of Mechanical Properties of Fluids. If you want more Free Learning Videos and Study Material Then don't forget to download the eSaral App.