What is a compound microscope - Ray Optics - eSaral

Compound Microscope is consists of two convergent lenses of short focal lengths. If you don't know what is a compound microscope then this article is for you.

Compound Microscope

Construction:

It consists of two convergent lenses of short focal lengths and apertures arranged co-axially lens (of focal length $\mathrm{f}_{\mathrm{O}}$) facing the object is called objective or field lens while the lens (of focal length $\mathrm{f}_{\mathrm{e}}$) facing the eye, eye-piece or ocular. The objective has a smaller aperture and smaller focal length than the eye-piece. the separation between objective and eye-piece can be varied.

Image Formation:

The object is placed between F and 2F of the objective so the image IM formed by objective (called intermediate image) is inverted, real enlarged and at a distance greater than $\mathrm{f}_{0}$ on the other side of the lens. This image IM acts as an object for the eye-piece and is within its focus. So, eye-piece forms final image I which is erect, Virtual, and enlarged with respect to intermediate image $\mathrm{I}_{\mathrm{M}}$. So, the final image I with respect to the object is Inverted, virtual, enlarged, and at a distance D to from eye on the same side of eye-piece as $\mathrm{I}_{\mathrm{M}}$. This all is shown in fig.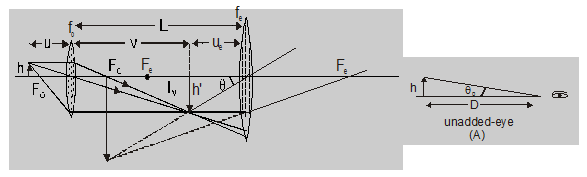


Magnifying power (MP) magnifying Power of an optical instrument is defined as –

$\mathrm{MP}=\frac{\text { Visual angle with instrument }}{\text { Max } \text { Visual angle for unadded eye }}$

$=\frac{\theta}{\theta_{0}}$

If the size of the object is h, and the least distance of distinct vision is D

$\theta_{0}=\frac{\mathrm{h}}{\mathrm{D}}$

$\theta=\frac{\mathrm{h}^{\prime}}{\mathrm{u}_{\mathrm{e}}}$ $\mathrm{MP}=\frac{\theta}{\theta_{0}}=\left[\frac{\mathrm{h}^{\prime}}{\mathrm{u}_{\mathrm{e}}}\right] \mathrm{x}\left[\frac{\mathrm{D}}{\mathrm{h}}\right]=\left[\frac{\mathrm{h}^{\prime}}{\mathrm{h}}\right]\left[\frac{\mathrm{D}}{\mathrm{u}_{\mathrm{e}}}\right]$

But for objective

$\mathrm{m}=\frac{1}{\mathrm{O}}=\frac{\mathrm{v}}{\mathrm{u}}$

i.e., $\quad \frac{\mathrm{h}^{\prime}}{\mathrm{h}}=-\frac{\mathrm{v}}{\mathrm{u}}[$ as $\mathrm{u}$ is - ve $]$

so $\mathrm{MP}=-\frac{\mathrm{v}}{\mathrm{u}}\left[\frac{\mathrm{D}}{\mathrm{u}_{\mathrm{e}}}\right]$

with the length of the tube

$L=v+u_{e}$......(1)

now there are two possibilities ­–

($\mathbf{b}_{1}$) If the final image is at infinity (far point) :

This situation is called normal adjustment as in this situation eye is least strained or relaxed. In this situation as for eye - piece $v=\infty$

$\frac{1}{-D}-\frac{1}{-u_{e}}=\frac{1}{f_{e}}$

i.e., $\frac{1}{\mathrm{u}_{\mathrm{e}}}=\frac{1}{\mathrm{D}}\left[1+\frac{\mathrm{D}}{\mathrm{f}_{\mathrm{e}}}\right]$

Substituting this value of ue in Eqn. (1), we have

$\mathrm{MP}=-\frac{\mathrm{v}}{\mathrm{u}}\left[1+\frac{\mathrm{D}}{\mathrm{f}_{\mathrm{e}}}\right]$

with $L=v+\frac{f_{e} D}{f_{e}+D}$.......(3)

In this situation as $\mathrm{u}_{\mathrm{e}}$ is minimum, MP is maximum and the eye is most strained.

In microscope focal length of objective lens $f_{0}$ is small and object is placed very closed to the objective lens so–

$\mathrm{u} \approx \mathrm{f}_{\circ}$ $\mathrm{L}=\mathrm{v}+\mathrm{u}_{\mathrm{e}}$

$\left[u_{e}< $\mathrm{L} \approx \mathrm{v}$ $|\mathrm{MP}|=\frac{\mathrm{LD}}{\mathrm{f}_{0} \mathrm{f}_{e}}$

Discussion :

1. The magnifying power of a microscope is negative so it produces final image always inverted.
   
   
2. $\mathrm{m}_{\mathrm{e}}=\frac{\mathrm{v}_{\mathrm{e}}}{\mathrm{u}_{\mathrm{e}}}=\frac{\mathrm{D}}{\mathrm{u}_{\mathrm{e}}}=\left[1+\frac{\mathrm{D}}{\mathrm{f}_{\mathrm{e}}}\right]$,
   
   $\mathrm{m}_{0}=\frac{\mathrm{v}_{0}}{\mathrm{u}_{0}}=\frac{\mathrm{v}}{\mathrm{u}}$
   
   $\mathrm{MP}=\mathrm{m}_{0} \times \mathrm{m}_{\mathrm{e}}$
   
   
3. $(\mathrm{MP})_{\min }=-\frac{\mathrm{V}}{\mathrm{u}} \frac{\mathrm{D}}{\mathrm{f}_{\mathrm{e}}}$
   
   $(\mathrm{MP})_{\max }=-\frac{\mathrm{v}}{\mathrm{u}}\left[1+\frac{\mathrm{D}}{\mathrm{f}_{\mathrm{e}}}\right]$
   
   
4. $|\mathrm{MP}|=-\frac{\mathrm{LD}}{\mathrm{f}_{0} \mathrm{f}_{\mathrm{e}}}$
   
   
5. MP does not change appreciably if the objective lens and eye-piece are interchanged
   
   $\left[\mathrm{MP} \sim\left(\mathrm{LD} / \mathrm{f}_{0} \mathrm{f}_{\mathrm{e}}\right)\right]$.
   
   MP is increased by decreasing the focal length of both lenses.
   
   
6. If the distance between the eye and eyepiece lens is D then distance between final image in eye-piece lens D' = (D – d)
   
   $\mathrm{MP}=\frac{\mathrm{LD}^{\prime}}{\mathrm{f}_{0} \mathrm{f}_{\mathrm{e}}}=\frac{\mathrm{L}(\mathrm{D}-\mathrm{d})}{\mathrm{f}_{0} \mathrm{f}_{\mathrm{e}}}$
   
   $=\mathrm{MP}\left[1-\frac{\mathrm{d}}{\mathrm{D}}\right]<\mathrm{MP}$
   
   
7. $\mathrm{RP}=\frac{1}{\mathrm{RL}} \alpha \frac{1}{\lambda}$ (Resolving power)
   
   
8. In electron microscope $\lambda=\sqrt{(150 / \mathrm{V})} \mathrm{A}$
   
   where : V = Potential difference
   
   

So, that's all from this article. I hope you get the idea about what is a compound microscope. If you liked this explanation then please share it with your friends. If you have any confusion related to this topic then feel free to ask in the comments section down below.

For a better understanding of this chapter, please check the detailed notes of  Chapter Ray Optics. To watch Free Learning Videos on physics by Saransh Gupta sir Install the eSaral App.