What is dynamic friction in physics - Friction, Class 11 - eSaral

Hey, do you want to know What is dynamic friction in physics? If yes. Then keep reading.

Dynamic Friction

When the force acting on the body is greater than the limiting friction, then the body comes into motion. The friction now acting between the surfaces of contact is dynamic friction.

The dynamic friction is always less than the limiting static friction.

Dynamic friction is of two types:

1. Sliding Friction
2. Rolling Friction

Sliding Friction:

If one body begins to slides over the other, then the friction between the surfaces is called sliding friction.

If the limiting kinetic friction force is $\mathrm{F}_{\mathrm{k}}$ and the normal reaction is N.

Then the coefficient of kinetic friction is given by $\mu_{\mathrm{k}}=\frac{\mathrm{F}_{\mathrm{k}}}{\mathrm{N}}$

If on the moving body an external force F acts, then in the presence of kinetic friction, the acceleration produced in the body is given by

$a=\frac{F-F_{k}}{m}$

where m is the mass of the body, and $F_{k}=\mu_{k} N$

Where the proportionality constant $\mu_{k}$ is a dimensionless number and is called the coefficient of kinetic friction. $\mu_{k}$ connects only the magnitudes of $F_{k}$ and N. These forces have perpendicular directions and $F_{k}$ is opposite v.

Note:

1. $\mu_{k}$ depends on the nature and condition of the two surfaces, and $\mu_{k}$ usually falls in the range from about 0.1 to about 1.5.
2. $\mu_{k}$ is nearly independent of speed for low relative speeds of the surfaces, decreasing slightly as the speed increases. We shall use the approximation that $F_{k}$ is independent of the speed.
3. $F_{k}$ (or $\mu_{k}$) is nearly independent of the area of contact for a wide range of areas.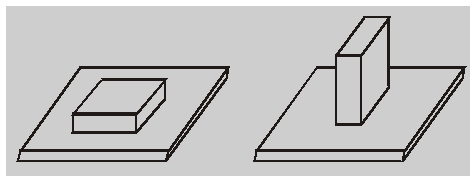The near independence of $\mu_{k}$ on the area of contact can be demonstrated by sliding a block that has sides with different areas. The surface of each side should consist of the same type of material and should be in the same condition. When the applied force required to slide the block at a given speed on different sides is measured, it is found to be nearly the same. Since N is the same in each case, we conclude that $\mu_{k}$ is approximately independent of the area.
   
   Similar to $\mu_{k}$, coefficient $\mu_{s}$ depends on the condition and nature of the two surfaces and is nearly independent of the area of contact.
   
   
   
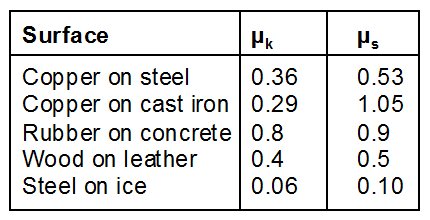
   Table lists $\mu_{k}$ and $\mu_{S}$ for a few representative pairs of surfaces. Normally, for a given pair of surfaces, $\mu_{S}$ is noticeably larger than $\mu_{\mathrm{k}}$.
   
   When two copper plates are highly polished and placed in contact with each other, then instead of decreasing, the force of friction increases. This arises due to the fact that for two highly polished surfaces in constant, the number of molecules coming in contact increases and as a result the adhesive forces increase. This in turn, increases the force of friction.

Rolling Friction:

When a body (say wheel) rolls on a surface the resistance offered by the surface is called rolling friction.

The velocity of the point of contact with respect to the surface remains zero.

The rolling friction is negligible in comparison to static or kinetic friction which may be present simultaneously i.e., $\mu_{\mathrm{R}}<\mu_{\mathrm{K}}<\mu_{\mathrm{S}}$

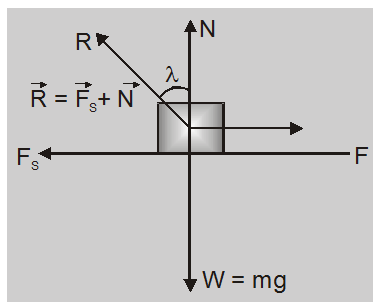
Angle of Friction

The angle of friction is the angle which the resultant of limiting friction $\mathrm{F}_{\mathrm{S}}$ and normal reaction N makes with the normal reaction. It is represented by $\lambda$, Thus from the figure.



$\tan \lambda=\frac{\mathrm{F}_{\mathrm{S}}}{\mathrm{N}}$

$\left(\because \mathrm{F}_{\mathrm{s}}=\mu \mathrm{N}\right)$

Or

$\tan \lambda=\mu$

For smooth surfaces,

$\lambda=0$ (zero)

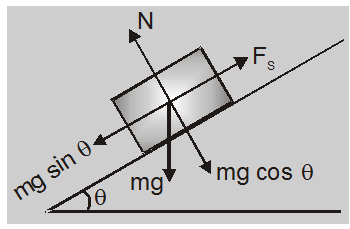
Angle of Repose ($\theta$)

If a body is placed on an inclined plane and if its angle of inclination is gradually increased, then at some angle of inclination $\theta$ the body will just on the point to slide down.



The angle is called angle of repose ($\theta$).

$\mathrm{F}_{\mathrm{S}}$ = mg $\sin \theta$ and N = mg $\cos \theta$

So

$\frac{F_{s}}{N}=\tan \theta$

Or

$\mu=\tan \theta$

Relation between angle of friction ($\lambda$) and angle of repose ($\theta$)

We know that tan $\lambda=\mu$ and $\mu=\tan \theta$

hence $\tan \lambda=\tan \theta$ or $\theta=\lambda$

Thus, angle of repose = angle of friction

So, that's all from this blog. I hope you get the idea of What is dynamic friction in physics. If you liked this explanation then please share it with your friends.

If you have any confusion related to this article then feel free to ask in the comments section down below.

Also read
What is Static Friction

To watch Free Learning Videos on physics by Saransh Gupta sir Install the eSaral App.