What is Horizontal Projectile Motion?

Horizontal Projectile Motion

Suppose a body is thrown horizontally from point $\mathrm{O}$, with velocity $\mathrm{u}$. Height of $\mathrm{O}$ from ground $=\mathrm{H}$. Let $X$-axis be along horizontal and $Y$-axis be vertically downwards and origin $O$ is at point of projection as shown in fig.

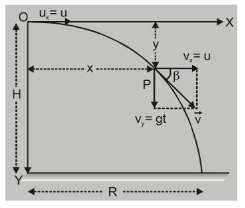Let the particle be at $P$ at a time $t$. The coordinates of $P$ are $(x, y)$.

Distance traveled along X-axis at time t with uniform velocity

i.e. velocity of projection and without acceleration.

i.e. velocity of projection and without acceleration.

The horizontal component of velocity $v_{x}=u$

and horizontal displacement $x=u, t$         ...(i)

displacement along the vertical direction is y to calculate $y$, consider the vertical motion of the projectile initial velocity in vertical direction $u_{y}=0$.

acceleration along y direction $\mathrm{a}_{\mathrm{y}}=\mathrm{g}$ (acc. due to gravity)

So $\quad v_{y}=a_{y} t \quad$ ( $y$ comp. of velocity at time t)

or $\quad v_{y}=g t \quad$ (as..(ii) $\quad$ (as body were dropped from a height)

Resultant velocity at time $t$ is $\vec{v}=u \hat{i}+(g t) \hat{j}$

$v=\sqrt{u^{2}+(g t)^{2}}$

or $\quad y=\frac{1}{2} g \cdot\left(\frac{x}{u}\right)^{2}$      [from equation (i) $t=\frac{x}{u}$]

or $\quad y=\frac{g}{2 u^{2}} \cdot x^{2}$

or $\quad y=k x^{2}$      here $k=\frac{g}{2 u^{2}}$ ( $k$ is constant)

This is eqn. of a parabola.

A body thrown horizontally from a certain height above the ground follows a parabolic trajectory till it hits the ground.

(i) Time of flight $\mathrm{T}=\sqrt{\frac{2 \mathrm{H}}{\mathrm{g}}}$    [as $\mathrm{y}=\frac{1}{2} \mathrm{gt}^{2}, \mathrm{~T}=\sqrt{\frac{2 \mathrm{H}}{\mathrm{g}}}$ ]

(ii) Range $\Rightarrow$ horizontal distance covered $=\mathrm{R}$.

$\mathrm{R}=\mathrm{u} \times$ time of flight

$\mathrm{R}=\mathrm{u} \cdot \sqrt{\frac{2 \mathrm{H}}{\mathrm{g}}}$  [ $\because H=\frac{g}{2 u^{2}} \mathrm{R}^{2}$ ]

(iii) Velocity when it hits the ground $\mathrm{v}_{\mathrm{g}}=\sqrt{\mathrm{u}^{2}+2 \mathrm{gH}}$

Ex. A projectile is fired with a horizontal velocity of $330 \mathrm{~ms}^{-1}$ from the top of a cliff $80 \mathrm{~m}$ high. How long will it take to strike the ground at the base of the cliff? With what velocity will it strike? Neglect air resistance.

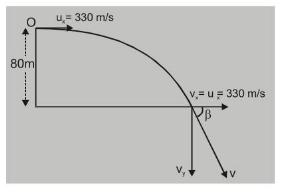Sol. Let us consider the vertically downward motion.

'u' $=0, \quad \mathrm{a}=+9.8 \mathrm{~m} / \mathrm{s}^{2}, \quad \mathrm{~S}=80 \mathrm{~m} \mathrm{t}=?$,

Using $S=u t+\frac{1}{2}$ at $^{2}$, we get $80=\frac{1}{2} \times 9.8 t^{2}$

or $\quad \mathrm{t}^{2}=\frac{160}{9.8}=16.33 \quad \Rightarrow \quad \mathrm{t}=4.04 \mathrm{sec}$

Distance from base $R=$ ut $=330 \times 4.04=1333.20 \mathrm{~m}$.

Now, $\quad v_{y}=u_{y}+a_{y} t=9.8 \times 4.04 \mathrm{~ms}^{-1}=39.59 \mathrm{~m} / \mathrm{s}$

Speed $=\sqrt{330^{2}+39.59^{2}}=332.37 \mathrm{~m} / \mathrm{s}$

and $\quad \tan \beta=\frac{39.59}{330}=0.12 \Rightarrow \quad \beta=6.84^{\circ}$

Ex. A bomb is dropped from an aeroplane flying horizontal with a velocity of $720 \mathrm{~km} / \mathrm{h}$ at an altitude of $980 \mathrm{~m}$. After what time, the bomb will hit the ground?

Sol. $t=\sqrt{\frac{2 h}{g}}=\sqrt{\frac{2 \times 980}{9.8}} \mathrm{~s}=10 \sqrt{2} \mathrm{sec}=14.14 \mathrm{sec}$

Ex. A horizontal stream of water leaves an opening in the side of a tank. If the opening is $\mathrm{h}$ metre above the ground and the stream hits the ground D metre away, then what is the speed of water as it leaves the tank in terms of $\mathrm{g}$, $\mathrm{h}$ and $\mathrm{D}$ ?

Sol. The given problem is the problem of horizontal projectile. The stream of water shall follow the parabolic path.

Now, $\quad t=\sqrt{\frac{2 h}{g}} ; v=\frac{D}{t}=D \sqrt{\frac{g}{2 h}}$.

Also Read

JEE Physics Notes

To watch Free Learning Videos on JEE by Kota’s top IITian Faculties Install the eSaral App