
Motion in Two Dimensions
An object moving in a plane is said to have two-dimensional motion. The two-dimensional motion is equal to the vector sum of two one-dimensional motions along the mutually perpendicular direction.
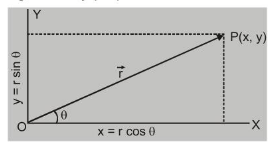
Let the position of point $P$ at a time $t$ be given by position
vector $\overrightarrow{\mathrm{OP}}=\overrightarrow{\mathrm{r}}$
$\vec{r}=\hat{i} r \cos \theta+\hat{j} r \sin \theta=\hat{i} x+\hat{j} y$
Also Read
JEE Physics Notes
To watch Free Learning Videos on JEE by Kota’s top IITian Faculties Install the eSaral App
Comments
"two dimensional"
June 13, 2023, 4:02 p.m.
To explain this example, Carl Sagan gives the example that suppose a living creature is confined on a page. Since the page consists of x and y axes (i.e. length and width), this creature is a two-dimensional (2D) world. For complete blogs click on given below link.
alifyar.com/kya-hamari-dunya-10-dimension-hai-dimensions-ka-khail
