Motion of Bodies in Contact
(a) When two bodies of masses $m_{1}$ and $m_{2}$ are kept on the frictionless surface and a force $F$ is applied on one body, then the force with which one body presses the other at the point of contact is called Force of Contact.
These two bodies will move with same acceleration $=\mathrm{a}$.
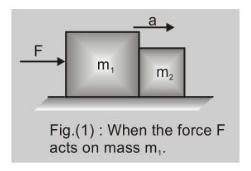When the force $F$ acts on the body with mass $m_{1}$
as shown in fig. (1) and (1a) $F=\left(m_{1}+m_{2}\right)$ a.
If the force exerted by $m_{2}$ on $m_{1}$ is $f_{1}$ (force of contact)
then for body $m_{1}$
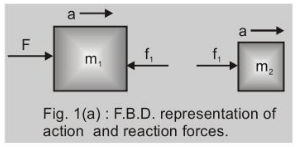$\left(F-f_{1}\right)=m_{1} a$
or $\quad f_{1}=F-m_{1} a$
$=\left(m_{1}+m_{2}\right) a-m_{1} a=m_{2} a$
or action on $\mathrm{m}_{2}, \mathrm{f}_{1}=\mathrm{m}_{2} \cdot \frac{\mathrm{F}}{\mathrm{m}_{1}+\mathrm{m}_{2}}$
When the force $F$ acts on the body with mass $m_{2}$ as shown in fig. 2 and $2(a)$
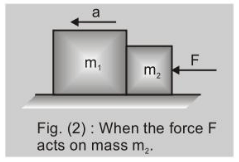$\mathrm{F}=\left(\mathrm{m}_{1}+\mathrm{m}_{2}\right) \mathrm{a}$
for body with mass $m_{2}$
$F-f_{2}=m_{2} a$
or $\quad f_{2}=F-m_{2} a$
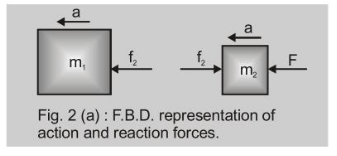$=\left(m_{1}+m_{2}\right) a-m_{2} a=m_{1} a$
or action on $m_{1}, \quad f_{2}=\frac{m_{1} F}{m_{1}+m_{2}}$
Also Read
JEE Physics Notes
To watch Free Learning Videos on JEE by Kota’s top IITian Faculties Install the eSaral App