JEE Main Previous Year Question of Physics with Solutions are available here. Practicing JEE Main Previous Year Papers Questions of Physics will help all the JEE aspirants in realizing the question pattern as well as help in analyzing their weak & strong areas.
Get detailed Class 11th &12th Physics Notes to prepare for Boards as well as competitive exams like IIT JEE, NEET etc.
eSaral helps the students in clearing and understanding each topic in a better way. eSaral is providing complete chapter-wise notes of Class 11th and 12th both for all subjects.
Besides this, eSaral also offers NCERT Solutions, Previous year questions for JEE Main and Advance, Practice questions, Test Series for JEE Main, JEE Advanced and NEET, Important questions of Physics, Chemistry, Math, and Biology and many more.
Download eSaral app for free study material and video tutorials.
Simulator
Previous Years AIEEE/JEE Main Questions
Q. The potential energy function for the force between two atoms in a diatomic molecule is approximately given by $\mathrm{U}(\mathrm{x})=\frac{\mathrm{a}}{\mathrm{x}^{12}}-\frac{\mathrm{b}}{\mathrm{x}^{6}}$ , where a and b are constant and x is the distance between the atoms. if the dissociation energy of the molecule is $\left[\mathrm{U}(\mathrm{x}=\infty)-\mathrm{U}_{\text {at equilibrium }}\right], \mathrm{D}$ is :
( 1)$\frac{b^{2}}{6 a}$
( 2)$\frac{\mathrm{b}^{2}}{2 \mathrm{a}}$
(3) $\frac{b^{2}}{12 a}$
(4) $\frac{\mathrm{b}^{2}}{4 \mathrm{a}}$
[AIEEE-2010]
Ans. (4)
$\mathrm{U}(\mathrm{x}=\infty)=0,$ at equilibrium
$\frac{\mathrm{d} \mathrm{U}}{\mathrm{dx}}=0 ;-\frac{12 \mathrm{a}}{\mathrm{x}^{13}}+\frac{6 \mathrm{b}}{\mathrm{x}^{7}}=0 \Rightarrow \mathrm{x}^{6}=\frac{2 \mathrm{a}}{\mathrm{b}}$
Q. At time t = 0s particle starts moving along the x-axis. If its kinetic energy increases uniformly with time 't', the net force acting on it must be proportional to :-
(1) $\sqrt{t}$
(2) constant
(3) t
(4) $\frac{1}{\sqrt{t}}$
[AIEEE-2011]
Ans. (4)
$\frac{1}{2} \mathrm{mv}^{2}=\mathrm{kt}$
$\mathrm{v}=\sqrt{\frac{2 \mathrm{kt}}{\mathrm{m}}}$
$\frac{\mathrm{d} \mathrm{v}}{\mathrm{dt}}=\sqrt{\frac{\mathrm{k}}{2 \mathrm{mt}}}$
$\mathrm{F}=\mathrm{m} \cdot \frac{\mathrm{d} \mathrm{v}}{\mathrm{dt}}$
$\mathrm{F} \propto \frac{1}{\sqrt{\mathrm{t}}}$
Q. This question has Statement-1 and Statement-2. Of the four choices given after the statements, choose the one that best describes the two statements.
If two springs $\mathrm{S}_{1}$ and $\mathrm{S}_{2}$ of force constants $\mathrm{k}_{1}$ and $\mathrm{k}_{2}$, respectively, are stretched by the same force, it is found that more work is done on spring $\mathrm{S}_{1}$ than on spring $\mathrm{S}_{2}$.
Statement-1: If stretched by the same amount, work done on $\mathrm{S}_{1}$, will be more than that on $\mathrm{S}_{2}$
Statement-2 : $\mathrm{k}_{1}$ < $\mathrm{k}_{2}$
(1) Statement-1 is true, Statement-2 is true and Statement-2 is not the correct explanation of Statement-1.
(2) Statement-1 is false, Statement-2 is true
(3) Statement-1 is true, Statement-2 is false
(4) Statement-1 is true, Statement-2 is true and Statement-2 is the correct explanation of statement-1.
[AIEEE-2012]
Ans. (2)
Given same force $\mathrm{F}=\mathrm{k}_{1} \mathrm{x}_{1}=\mathrm{k}_{2} \mathrm{x}_{2}$
$\Rightarrow \frac{\mathrm{k}_{1}}{\mathrm{k}_{2}}=\frac{\mathrm{x}_{2}}{\mathrm{x}_{1}}$
$\mathrm{W}_{1}=\frac{1}{2} \mathrm{k}_{1} \mathrm{x}_{1}^{2} \& \mathrm{W}_{2}=\frac{1}{2} \mathrm{k}_{2} \mathrm{x}_{2}^{2}$
As $\frac{\mathrm{W}_{1}}{\mathrm{W}_{2}}>1$ so $\frac{\frac{1}{2} \mathrm{k}_{1} \mathrm{x}_{1}^{2}}{\frac{1}{2} \mathrm{k}_{2} \mathrm{x}_{2}^{2}}>1$
$\Rightarrow \frac{\mathrm{Fx}_{1}}{\mathrm{Fx}_{2}}>1 \Rightarrow \frac{\mathrm{k}_{2}}{\mathrm{k}_{1}}>1$
$\therefore \mathrm{k}_{2}>\mathrm{k}_{1}$ statement 2 is true
OR
if $\mathrm{x}_{1}=\mathrm{x}_{2}=\mathrm{x}$
$\frac{\mathrm{W}_{1}}{\mathrm{W}_{2}}=\frac{\frac{1}{2} \mathrm{K}_{1} \mathrm{x}^{2}}{\frac{1}{2} \mathrm{K}_{2} \mathrm{x}^{2}}=\frac{\mathrm{K}_{1}}{\mathrm{K}_{2}}$
$\therefore \frac{\mathrm{W}_{1}}{\mathrm{W}_{2}}=\frac{\mathrm{K}_{1}}{\mathrm{K}_{2}}<1$
$\therefore \mathrm{W}_{1}<\mathrm{W}_{2}$
statement 1 is false
Q. When a rubber-band is stretched by a distance x, it exerts a restoring force of magnitude $\mathrm{F}=\mathrm{ax}+\mathrm{bx}^{2}$ where a and b are constants. The work done in stretching the unstretched rubber-band by L is:-
(1) $\frac{\mathrm{aL}^{2}}{2}+\frac{\mathrm{bL}^{3}}{3}$
(2) $\frac{1}{2}\left(\frac{\mathrm{aL}^{2}}{2}+\frac{\mathrm{b} \mathrm{L}^{3}}{3}\right)$
(3) aL $^{2}+\mathrm{bL}^{3}$
(4) $\frac{1}{2}\left(\mathrm{aL}^{2}+\mathrm{bL}^{3}\right)$
[JEE-Mains-2014]
Ans. (1)
Work done $=\int_{0}^{\mathrm{L}} \mathrm{Fdx}$
$=\int_{0}^{\mathrm{L}}\left(\mathrm{ax}+\mathrm{bx}^{2}\right) \mathrm{d} \mathrm{x}$
$=\frac{\mathrm{aL}^{2}}{2}+\frac{\mathrm{bL}^{3}}{3}$
Q. A person trying to lose weight by burning fat lifts a mass of 10 kg upto a height of 1 m 1000 times. Assume that the potential energy lost each time he lowers the mass is dissipated. How much fat will he use up considering the work done only when the weight is lifted up? Fat supplies $3.8 \times 10^{7}$ J of energy per kg which is converted to mechanical energy with a 20% efficiency rate. Take g = 9.8 $\mathrm{ms}^{-2}$ :-
(1) $12.89 \times 10^{-3} \mathrm{kg}$
(2) $2.45 \times 10^{-3} \mathrm{kg}$
(3) $6.45 \times 10^{-3} \mathrm{kg}$
(4) $9.89 \times 10^{-3} \mathrm{kg}$
[JEE-Mains-2016]
Ans. (1)
Work done against gravity = (mgh) 1000
in lifting 1000 times
$=10 \times 9.8 \times 10^{3}$
$=9.8 \times 10^{4}$ Joule
$20 \%$ efficiency is to converts fat into energy.
$\left[20 \% \text { of } 3.8 \times 10^{7} \mathrm{J}\right] \times(\mathrm{m})=9.8 \times 10^{4}$
(Where m is mass)
$\mathrm{m}=12.89 \times 10^{-3} \mathrm{kg}$
Q. A point particle of mass, moves along the uniformly rough track PQR as shown in the figure. The coefficient of friction, between the particle and the rough track equals . The particle is released, from rest, from the point P and it comes to rest at a point R. The energies, lost by the ball, over the parts, PQ and PR, of the track, are equal to each other, and no energy is lost when particle changes direction from PQ to QR. The values of the coefficient of friction $\mu$ and the distance x(=QR) are, respecitvely close to :
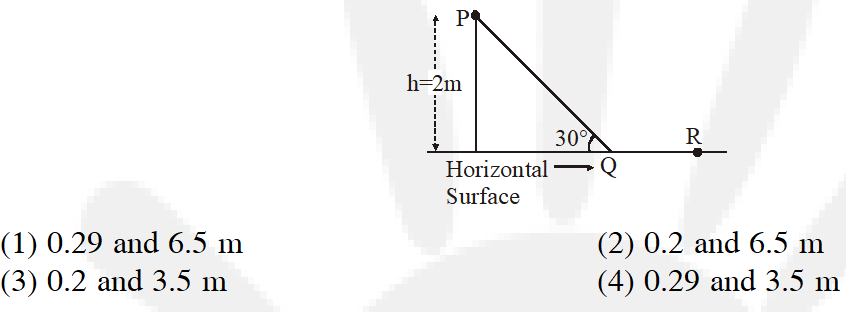[JEE-Mains-2016]
[JEE-Mains-2016]
Ans. (4)
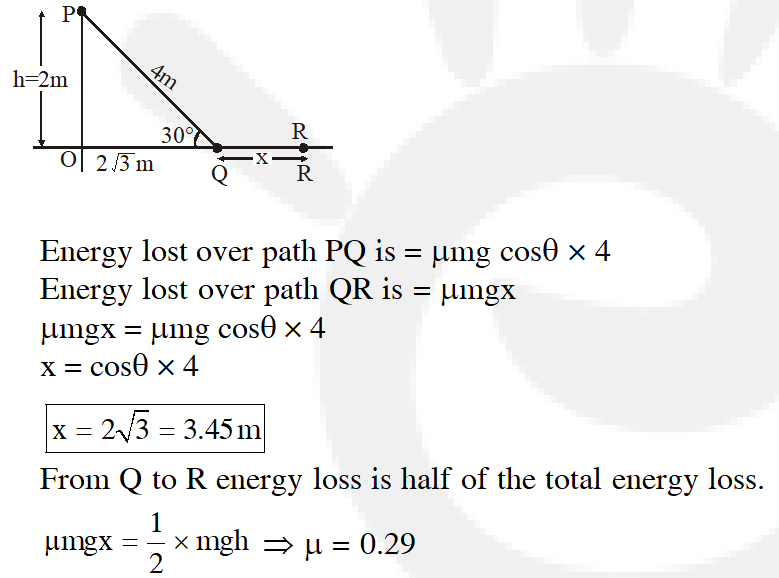
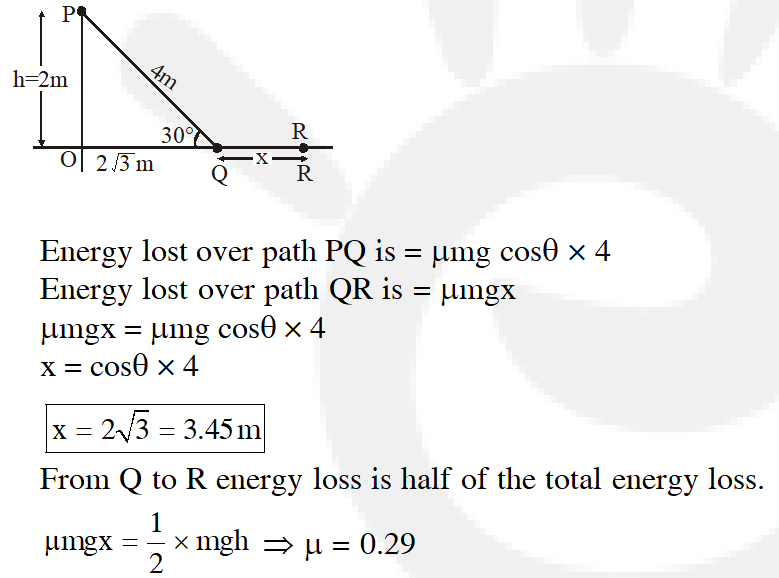
Q. A body of mass m $=10^{-2}$ kg is moving in a medium and experiences a frictional force F = $-\mathrm{K} \mathrm{V}^{2}$. Its intial speed is $\mathrm{v}_{0}$ = 10 $\mathrm{ms}^{-1}$. If, after 10 s, its energy is , the value of k will be :-
(1) $10^{-4} \mathrm{kg} \mathrm{m}^{-1}$
(2) $10^{-1} \mathrm{kg} \mathrm{m}^{-1} \mathrm{s}^{-1}$
(3) $10^{-3} \mathrm{kg} \mathrm{m}^{-1}$
(4) $10^{-3} \mathrm{kg} \mathrm{s}^{-1}$
[JEE MAINS-2017]
Ans. (1)
$\frac{1}{2} \mathrm{mv}_{\mathrm{f}}^{2}=\frac{1}{8} \mathrm{mv}_{0}^{2}$
$\mathrm{v}_{\mathrm{f}}=\frac{\mathrm{v}_{0}}{2}=5 \mathrm{m} / \mathrm{s}$
$\left(10^{-2}\right) \frac{d V}{d t}=-k v^{2}$
$\int_{10}^{5} \frac{\mathrm{dv}}{\mathrm{v}^{2}}=-100 \mathrm{k} \int_{0}^{10} \mathrm{dt}$
$\frac{1}{5}-\frac{1}{10}=100 \mathrm{k}(10)$
$\mathrm{k}=10^{-4}$
Q. A time dependent force F = 6t acts on a particle of mass 1 kg. If the particle starts from rest, the work done by the force during the first 1 sec. will be :
(1) 9 J (2) 18 J (3) 4.5 J (4) 22 J
[JEE MAINS-2017]
Ans. (3)
F = 6t = ma
$\Rightarrow \mathrm{a}=6 \mathrm{t}$
$\Rightarrow \frac{\mathrm{dv}}{\mathrm{dt}}=6 \mathrm{t}$
$\int_{0}^{\mathrm{v}} \mathrm{d} \mathrm{v}=\int_{0}^{1} 6 \mathrm{t} \mathrm{dt}$
$\mathrm{v}=\left(3 \mathrm{t}^{2}\right)_{0}^{1}=3 \mathrm{m} / \mathrm{s}$
From work energy theorem
$\mathrm{W}_{\mathrm{F}}=\Delta \mathrm{K.E}=\frac{1}{2} \mathrm{m}\left(\mathrm{v}^{2}-\mathrm{u}^{2}\right)$
$=\frac{1}{2}(1)(9-0)=4.5 \mathrm{J}$
Q. A particle is moving in a circular path of radius a under the action of an attractive potential $\mathrm{U}=-\frac{\mathrm{k}}{2 \mathrm{r}^{2}} .$ Its total energy is :-.
(1) $\frac{\mathrm{k}}{2 \mathrm{a}^{2}}$
(2) Zero
(3) $-\frac{3}{2} \frac{\mathrm{k}}{\mathrm{a}^{2}}$
$(4)-\frac{\mathrm{k}}{4 \mathrm{a}^{2}}$
[JEE MAINS-2018]
Ans. (2)
$\mathrm{F}=-\frac{\partial \mathrm{u}}{\partial \mathrm{r}}=\frac{\mathrm{K}}{\mathrm{r}^{3}}$
Since it is performing circular motion
$\mathrm{F}=\frac{\mathrm{mv}^{2}}{\mathrm{r}}=\frac{\mathrm{K}}{\mathrm{r}^{3}}$
$\mathrm{mv}^{2}=\frac{\mathrm{K}}{\mathrm{r}^{2}}$
$\Rightarrow \mathrm{K.E.}=\frac{1}{2} \mathrm{mv}^{2}=\frac{\mathrm{K}}{2 \mathrm{r}^{2}}$
Total energy = P.E. + K.E.
$=-\frac{\mathrm{K}}{2 \mathrm{r}^{2}}+\frac{\mathrm{K}}{2 \mathrm{r}^{2}}=\mathrm{Zero}$
Comments
sudharsan k
Oct. 31, 2020, 11:39 p.m.
questions are pretty good and solutions seems comfortable thanks if it helped me in my exams
Zayn Malik and Gigi Hadid
Sept. 26, 2020, 9:33 p.m.
Hey guys!!! This is Zayn and Gigi...We are very much looking forward to pursue our newborn's education in India...Please suggest the best city!
Thank you
Yours,
Z and G
kejf'foryufhiogs'gjruputirboyvi'paeurf90shgiofgjgiflgu0uyidpj is my name...lol
Sept. 26, 2020, 9:03 p.m.
Stained coffee cup
Just a fingerprint of lipstick's not enough
Sleep, where you lay
Still a trace of innocence on the pillow case
Waking up
Beside you, I'm my loaded gun
I can't contain this anymore
I'm all yours, I've got no control
No control
Powerless
And I don't care, it's obvious
I just can't get enough of you
The pedal's down, my eyes are closed
No control
Got the taste on my tongue
I don't want to wash away the night before
And the heat where you laid
I could stay right here and burn in it all day
Waking up
Beside you, I'm my loaded gun
I can't contain this anymore
I'm all yours, I've got no control
No control
Powerless
And I don't care, it's obvious
I just can't get enough of you
The pedal's down, my eyes are closed
No control
Lost my senses
I'm defenseless
Her…
(No Control~One Direction)
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.