A Telescope is an optical instrument used to increase the visual angle of distant large objects such as a star a planet. If you want to learn about the Working of a Telescope then keep reading.
Telescope
It is an optical instrument used to increase the visual angle of distant large objects such as a star a planet or a cliff etc. An astronomical telescope consists of two converging lenses. The one facing the object is called an objective or field - lens and has a large focal length and aperture, the distance between the two lenses is adjustable.
A telescope is used to see distant objects, in its object is between $\infty$ and 2F of objective and hence image formed by objective is real, inverted, and diminished and is between F and 2F on the other side of it. This image (called intermediate image) acts as an object for the eyepiece and shifting the position of the eye-piece is brought within its focus. So final image I, with respect to the intermediate image, is erect, virtual, enlarged, and at a distance D to $\infty$ from the eye. This in turns implies that the final image with respect to the object is inverted, enlarged, and at a distance D to $\infty$ from the eye.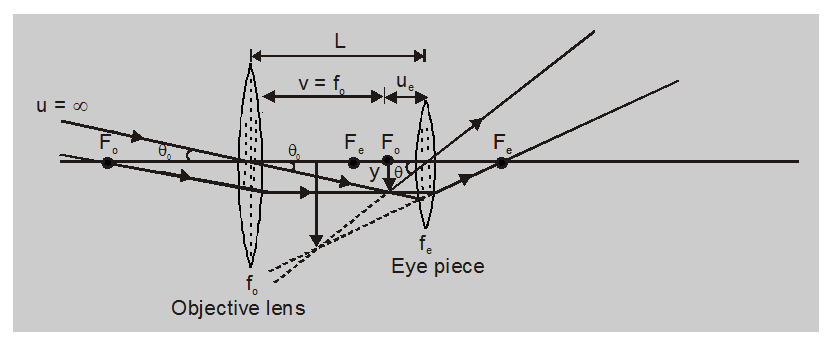
Magnifying Power (MP)
magnifying Power of a telescope is defined as
$\mathrm{MP}=\frac{\text { Visual angle with instrument }}{\text { Visual angle for unadded eye }}$
$=\frac{\theta}{\theta_{0}}$
But from fig.
$\theta_{0}=\left(y / f_{0}\right)$ and $\theta=\left(y /-u_{e}\right)$
So $\mathrm{MP}=\frac{\theta}{\theta_{0}}=-\left[\frac{\mathrm{f}_{0}}{\mathrm{u}_{\mathrm{e}}}\right]$ with length of tube
$\mathrm{L}=\left(\mathrm{f}_{0}+\mathrm{u}_{\mathrm{e}}\right)$.......(1)
Now there are two possibilities –
(a) If the final image is at infinity (far point)
This situation is called normal adjustment as in this situation eye is least strained or relaxed. In this situation as for eye - piece v = $\infty$
$\frac{1}{-\infty}-\frac{1}{u_{e}}=\frac{1}{f_{e}}$
i.e. $u_{e}=f_{e}$
So substituting this value of ue in Eqn. (1) we have
$\mathrm{MP}=-\left(\mathrm{f}_{0} / \mathrm{f}_{\mathrm{e}}\right)$
and $L=\left(f_{0}+f_{e}\right)$.....(2)
Usually, the telescope operates in this mode unless stated otherwise. In this mode, as ue is maximum for a given telescope MP is minimum while the length of tube maximum. In this case, the object and final image are at infinity so both total lights entering and leave the telescope are parallel to its axis as shown in fig.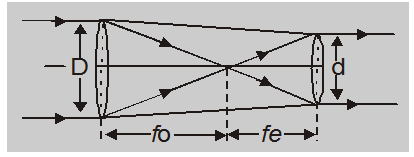
(b) If the final image is at D (Near point)
In this situation as for eye - piece v = D
$\frac{1}{-D}-\frac{1}{-u_{e}}=\frac{1}{f_{e}}$
i.e., $\frac{1}{-u_{e}}=\frac{1}{f_{e}}\left[1+\frac{f_{e}}{D}\right]$
So substituting this value of ue in Eqn. (1), we have
$\mathrm{MP}=\frac{\mathrm{f}_{0}}{\mathrm{f}_{\mathrm{e}}}\left[1+\frac{\mathrm{f}_{\mathrm{e}}}{\mathrm{D}}\right]$
With
$L=f_{0}+\frac{f_{e} D}{f_{e}+D}$.....(3)
In this situation $\mathrm{u}_{\mathrm{e}}$ is minimum so for a given telescope MP is maximum while the length of tube minimum and the eye is most strained. In the case of a telescope if the object and final image are at infinity so both total lights entering and leave the telescope are parallel to its axis as shown in fig.
Note:
$\frac{\mathrm{f}_{0}}{\mathrm{f}_{\mathrm{e}}}=\frac{\text { Aperture of object }}{\text { Aperture of eye piece }}$
i.e.,
$\mathrm{MP}=\frac{\mathrm{f}_{0}}{\mathrm{f}_{\mathrm{e}}}=\frac{\mathrm{D}}{\mathrm{d}}$
So, that's all from this article. I hope you get the idea about the Working of Telescope. If you found this article informative then please share it with your friends. If you have any confusion related to this topic then you can ask in the comments section down below.
For a better understanding of this chapter, please check the detailed notes of Ray Optics. To watch Free Learning Videos on physics by Saransh Gupta sir Install the eSaral App.
