Young double slit experiment class 12 - Physics - eSaral

Hey, do you want to learn about the Young double-slit experiment? If yes. Then keep reading.

The experiment of young's Dual-slit

• This experiment shows interference of light
• $s_{1} \& s_{2}$ slit behaves like two coherent sources.
• On-Screen, Bright & Dark portions are alternatively found.
• The bright portion is called Bright fringe & the dark portion is called dark fringe.
• The central fringe is always bright.
• Energy conserves in interference of light.
• It is explained on the basis of hygen principle.
• This experiment verifies the wave nature of light.

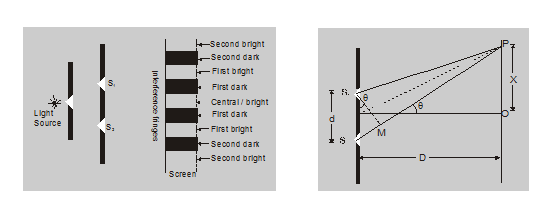
1. At a point on screen to find dark or bright fringe, it depends upon the path difference between $\mathrm{s}_{1} \mathrm{P}$ & $\mathrm{s}_{2} \mathrm{P}$ light waves.
   
   
2. Two types of path difference between light waves:
   (i) Geometrical path difference.
   (ii) Optical path difference.

In above experiment, optical difference s1P & s2P has geometrical path difference so, Total path difference = Geometrical difference

$\mathrm{s}_{1} \mathrm{P}-\mathrm{s}_{2} \mathrm{P}=\frac{\mathrm{xd}}{\mathrm{D}}$ (note $-\sin \theta \approx \tan \theta \approx Q)$

• Bright Fringes: If nth bright fringe forms at point P, then for Bright fringe:
  
  $\mathrm{S}_{2} \mathrm{P}-\mathrm{S}_{1} \mathrm{P}=\frac{\mathrm{X}_{\mathrm{n}} \mathrm{d}}{\mathrm{D}}=\mathrm{n} \lambda$
  
  $X_{n}=\frac{n \lambda D}{d}$
  
  So distance between central fringe & nth bright fringe :
  
  $X_{n}=\frac{n \lambda D}{d}$
  
  n = 1 first bright fringe
  n = 2 Second bright fringe
  
  
• Dark Fringe: If nth dark fringe forms at a point P, then for dark fringe.
  
  $\frac{X_{n} d}{D}=\frac{(2 n-1)}{2} \lambda \mid$
  
  distance between central fringe & nth fringe.
  
  $X_{n}=\frac{(2 n-1) \lambda D}{2 d}$
  n = 1 First bright fringe.
  n = 2 Second bright fringe.
  
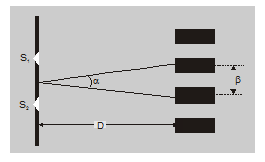
  Distance between dark & bright fringe which are incoming orders is called fringe width. In Interference Fringe width of dark & bright fringes are the same $\beta=\frac{\lambda D}{d}$
  
  
• The angular width of the fringe $\alpha \quad D=\beta$ $\alpha=\beta / D=\frac{\lambda}{d}$
  
  

Comments on young's interference experiment:

1. Energy is conserved in interference. This indicated that energy is redistributed from the destructive interference region to the constructive interference region.
   
   
2. If the entire arrangement of young's double-slit experiment is immersed in water then fringe width decreases $\frac{\beta_{\text {water }}}{\beta_{\text {air }}}=\frac{\lambda_{\text {water }}}{\lambda_{\text {air }}}=\frac{1}{a_{\mathrm{w}}}=\frac{1}{(4 / 3)}$
   
   
3. If white light is used in place of monochromatic light in young's double-slit experiment.
   
   (a) central fringe is white
   
   (b) Colored fringe around the central white fringe
   
   (c) Inner edge of the dark fringe is red. While the outer edge is violet (or blue)
   
   (d) Inner edge of the bright fringe is violet (or blue) and the outer edge is red.
   
   
4. If a filter allowing only $\lambda_{\text {red }}$ (of $\lambda_{1}$) is placed in front of slit $\mathrm{s}_{1}$ and filter allowing only $\lambda_{\text {blue }}\left(\right.$ or $\left.\lambda_{1}\right)$ is placed is front of slit $\mathrm{s}_{2}$. Then there is no interference pattern. (refer to point no.3 of conditions)
   
   
5. If a thin glass plate or mica sheet is placed in front of one of the slit, then the central fringe shifts towards that slit, the refractive index of glass is $\mu$ and the thickness of sheet t, then the optical path = $\mu \mathrm{t}$ so extra path difference $(\mu-1) t$
   
   If the central fringe now appears at the location of previously formed nth bright fringe then $(\mu-1) t$ $=n \lambda$ if the central fringe appears at the position of previously formed nth dark fringe then $(\mu-1) t$
   
   $=(2 n-1) \frac{\lambda}{2}$
   
   
6. If the width of the slit S increased then the degree of spatial coherence decreases. As a result the interference pattern gradually disappears similar occurs if the distance between $\mathrm{s}_{1}$ and $\mathrm{s}_{2}$ is increased.
   
   
7. The fringe visibility :
   
   $V=\frac{I_{\max }-I_{\min }}{I_{\max }+I_{\min }}$
   
   $V_{\max }:$ if $I_{1}=I_{2}=I_{0}$
   
   or $\mathrm{I}_{\min }=0$
   
   If widths of slits $\mathrm{s}_{1}$ and $\mathrm{s}_{2}$ are unequal the brightness of the bright fringe and the darkness of the dark fringe decreases.
   
   If $\left.\right|_{1}>>\left.\right|_{2}$ then $\left.\right|_{\max }=\left.\right|_{\min }$
   
   
8. When waves from two coherent sources $S_{1}$ are $S_{2}$ interfere in space the shape of the fringe is hyperbolic with foci at $\mathrm{S}_{1}$ and $\mathrm{S}_{2}$.
   
   

So, that's all from this article. I hope you get the idea about the Young double-slit experiment. If you found this article informative then please share it with your friends. If you have any confusion related to this topic then feel free to ask in the comments section down below.

For a better understanding of this chapter, please check the detailed notes of the Wave Optics. To watch Free Learning Videos on physics by Saransh Gupta sir Install the eSaral App.