JEE Main Previous Year Papers Questions of Chemistry With Solutions are available at eSaral.
Simulator
Previous Years AIEEE/JEE Mains Questions
Q. In an atom, an electron is moving with a speed of 600 m/s with an accuracy of 0.005%. Certainity with which the position of the electron can be located is ($\mathrm{Ch}=6.6 \times 10^{-34} \mathrm{kg} \mathrm{m}^{2} \mathrm{s}^{-1}$, mass of electron,
$\mathrm{e}_{\mathrm{m}}=9.1 \times 10^{-31} \mathrm{kg}$):-
(1) $1.92 \times 10^{-3} \mathrm{m}$
(2) $3.84 \times 10^{-3} \mathrm{m}$
(3) $1.52 \times 10^{-4} \mathrm{m}$
(4) $5.10 \times 10^{-3} \mathrm{m}$
[AIEEE-2009]
Ans. (1)
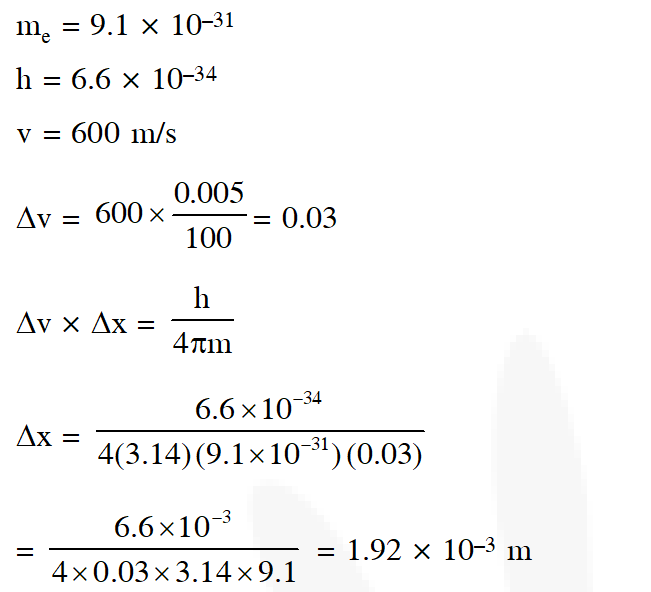
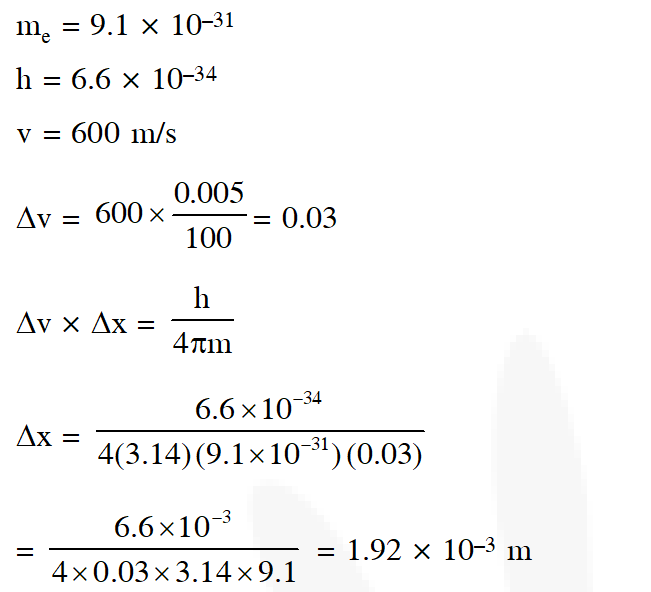
Q. Calculate the wavelength (in nanometer) associated with a proton moving at $1.0 \times 10^{3} \mathrm{ms}^{-1}$ (Mass of proton = $1.67 \times 10^{-27} \mathrm{kg}$ and $\mathrm{h}=6.63 \times 10^{-34} \mathrm{Js}$) :-
(1) 2.5 nm (2) 14.0 nm (3) 0.032 nm (4) 0.40 nm
[AIEEE-2009]
Ans. (4)
$\mathrm{m}_{\mathrm{p}}=1.67 \times 10^{-27}$
$\mathrm{h}=6.63 \times 10^{-34}$
$\mathrm{v}=10^{3}$
$\lambda=\frac{\mathrm{h}}{\mathrm{mv}}=\frac{6.63 \times 10^{-34}}{1.67 \times 10^{-27} \times 10^{3}}$
$=3.97 \times 10^{-7+3}$
$=3.97 \times 10^{-10}$
$=\frac{3.9 \times 10^{-10}}{10^{-9}} \mathrm{nm} \quad=0.40 \mathrm{nm}$
Q. The energy required to break one mole of Cl–Cl bonds in Cl2 is 242 kJ $\mathrm{mol}^{-1}$. The longest wavelength of light capable of breaking a single Cl–Cl bond is
$\left(\mathrm{C}=3 \times 10^{8} \mathrm{ms}^{-1} \text { and } \mathrm{N}_{\mathrm{A}}=6.02 \times 10^{23} \mathrm{mol}^{-1}\right)$
(1) 494 nm
(2) 594 nm
(3) 640 nm
(4) 700 nm
[AIEEE-2010]
Ans. (1)
$\mathrm{B.E.}=242 \mathrm{kJ} / \mathrm{mol}$
$\mathrm{E}=\frac{\mathrm{hcN}_{\mathrm{A}}}{\lambda}$
$10^{3} \times 242 \times \lambda=3 \times 10^{8} \times 6.626 \times 10^{-34} \times 6.02 \times 10^{23}$
$\lambda=\frac{3 \times 6.626 \times 6.02 \times 10^{-26+23}}{242}$
$=0.494 \times 10^{-3} \times 10^{-3}$
= 494 nm
Q. Ionisation energy of $\mathrm{He}^{+}$ is $19.6 \times 10^{-18} \mathrm{J}$ atom $^{-1}$. The energy of the first stationary state (n = 1) of $\mathrm{L} \mathbf{i}^{2+}$ is:-
(1) $8.82 \times 10^{-17} \mathrm{J}$ atom $^{-1}$
(2) $4.41 \times 10^{-16} \mathrm{J}$ atom $^{-1}$
(3) $-4.41 \times 10^{-17} \mathrm{J}$ atom $^{-1}$
(4) $-2.2 \times 10^{-15} \mathrm{J}$ atom $^{-1}$
[AIEEE-2010]
Ans. (3)
I.E. $=19.6 \times 10^{-18}$
I.E $\propto \mathrm{z}^{2}$
$\frac{(\mathrm{I.E.})_{\mathrm{Li}^{+2}}}{(\mathrm{I.E.})_{\mathrm{He}}}=\frac{\mathrm{Z}_{\mathrm{Li}}^{2}}{\mathrm{Z}_{\mathrm{He}}^{2}} \quad \mathrm{E}_{1}=\frac{9}{4} \times 19.6 \times 10^{-18}$
$=-4.41 \times 10^{-17}$
Q. The frequency of light emitted for the transition n = 4 to n = 2 of He+ is equal to the transition in H atom corresponding to which of the following
(1) n = 3 to n = 1 (2) n = 2 to n = 1 (3) n = 3 to n = 2 (4) n = 4 to n = 3
[AIEEE-2011]
Ans. (2)
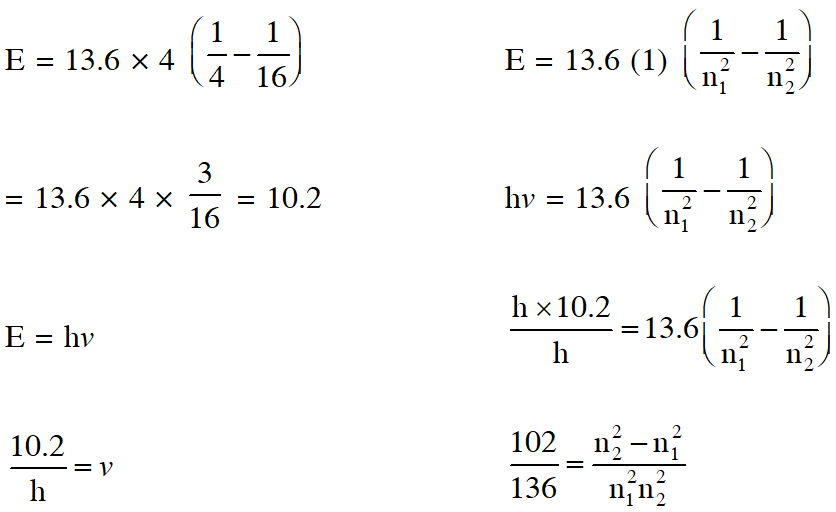
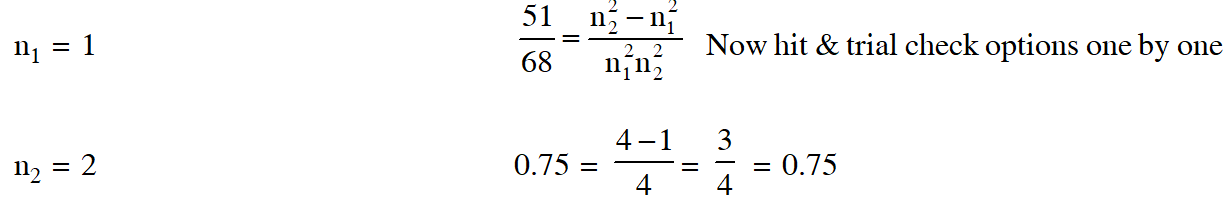
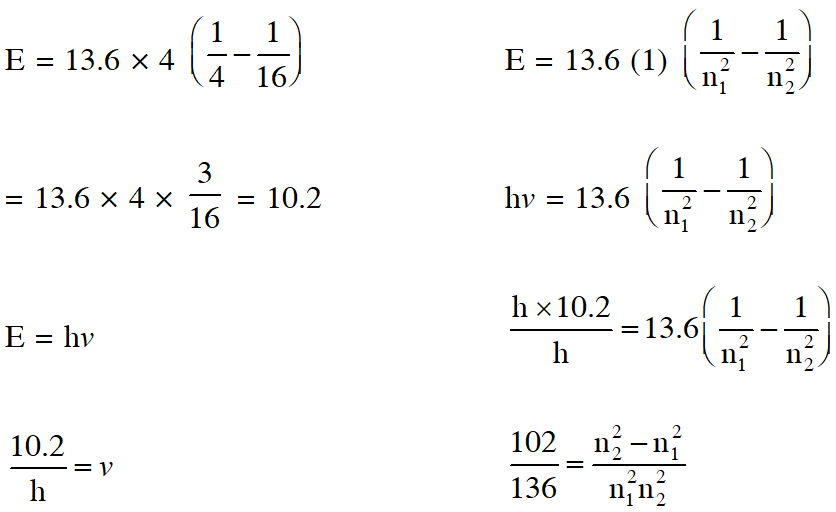
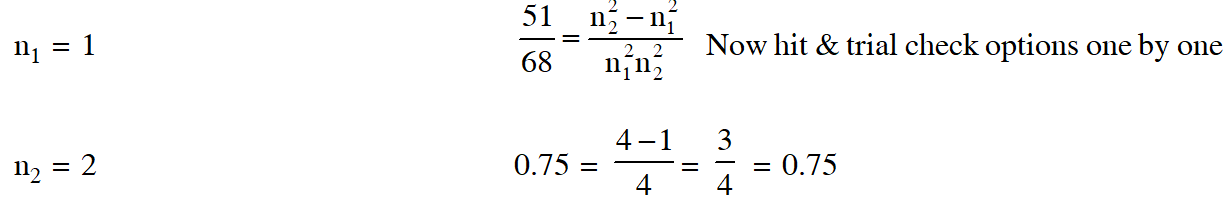
Q. The electrons identified by quantum numbers n and :-
(a) n = 4 , = 1
(b) n = 4, = 0
(c) n = 3, = 2
(d) n = 3, = 1
Can be placed in order of increasing energy as
(1) (a) < (c) < (b) < (d) (2) (c) < (d) < (b) < (a)
(3) (d) < (b) < (c) < (a) (4) (b) < (d) < (a) < (c)
(3) (d) < (b) < (c) < (a) (4) (b) < (d) < (a) < (c)
[AIEEE-2012]
Ans. (3)
(d) < (b) < (c) < (a) Acc. to (n + ) rule.
Q. If the kinetic energy of an electron is increased four times, the wavelength of the de-Broglie wave associated with it would become :-
(1) Two times
(2) Half
(3) One fourth
(4) Four time
[JEE-Main(online2012]
Ans. (2)
$\lambda \propto \frac{1}{\sqrt{\mathrm{KE}}}$
Q. The wave number of the first emission line in the Balmer series of H-Spectrum is :
(R = Rydberg constant) :
(1) $\frac{3}{4} \mathrm{R}$
(2) $\frac{9}{400} \mathrm{R}$
(3) $\frac{5}{36} \mathrm{R}$
(4) $\frac{7}{6} \mathrm{R}$
[JEE-Main(online) 2013]
Ans. (3)
$\bar{v}=\frac{1}{\mathrm{R}}\left(\frac{1}{2^{2}}-\frac{1}{3^{2}}\right)=\frac{5}{36 \mathrm{R}}$
Q. The de Broglie wavelength of a car of mass 1000 kg and velocity 36 km/hr is :
$\left(\mathrm{h}=6.63 \times 10^{-34} \mathrm{J} \mathrm{s}\right)$
(1) $6.626 \times 10^{-31} \mathrm{m}$
(2) $6.626 \times 10^{-34} \mathrm{m}$
(3) $6.626 \times 10^{-38} \mathrm{m}$
(4) $6.626 \times 10^{-30} \mathrm{m}$
[JEE-Main(online) 2013]
Ans. (3)
Q. For which of the following particles will it be most difficult to experimentally verify the de-Broglie relationship?
(1) a dust particle (2) an electron (3) a proton (4) an -particle.
[JEE-Main(online) 2014]
Ans. (1)
Q. If the binding energy of the electron in a hydrogen atom is 13.6 eV, the energy required to remove the electron from the first excited state of $\mathbf{L} \mathbf{i}^{++}$ is :
(1) 13.6 eV (2) 30.6 eV (3) 122.4 eV (4) 3.4 eV
[JEE-Main(online) 2014]
Ans. (2)
B.E. $=3.4 \times 9=30.6 \mathrm{eV}$
Q. Based on the equation
$\Delta \mathrm{E}=-2.0 \times 10^{-18} \mathrm{J}\left(\frac{1}{\mathrm{n}_{2}^{2}}-\frac{1}{\mathrm{n}_{1}^{2}}\right)$
the wavelength of the light that must be absorbed to excite hydrogen electron from level n = 1 to level n $=2$ will be $\left(\mathrm{h}=6.625 \times 10^{-34} \mathrm{Js}, \mathrm{C}=3 \times 10^{8} \mathrm{ms}^{-1}\right)$
(1) $2.650 \times 10^{-7} \mathrm{m}$
(2) $1.325 \times 10^{-7} \mathrm{m}$
(3) $1.325 \times 10^{-10} \mathrm{m}$
(4) $5.300 \times 10^{-10} \mathrm{m}$
[JEE-Main(online) 2014]
Ans. (2)
$\frac{1}{\lambda}=\frac{2 \times 10^{-18}}{\mathrm{hc}}\left[\frac{1}{(1)^{2}}-\frac{1}{(2)^{2}}\right]$
$\Rightarrow \frac{1}{\lambda}=\frac{2 \times 10^{-18}}{6.625 \times 10^{-34} \times 3 \times 10^{8}} \times \frac{3}{4}$
$\Rightarrow \lambda=\frac{2 \times 6.625 \times 10^{-34} \times 10^{8}}{10^{-18}}$
$=13.25 \times 10^{-8}$
$=1.325 \times 10^{-7} \mathrm{m}$
Q. If
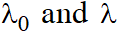be the threshold wavelength and wavelength of incident light, the velocity of photoelectron ejected from the metal surface is
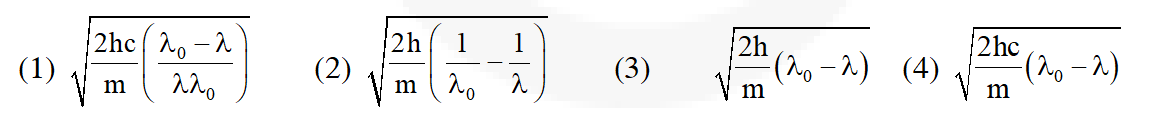[JEE-Main(online) 2014]
be the threshold wavelength and wavelength of incident light, the velocity of photoelectron ejected from the metal surface is
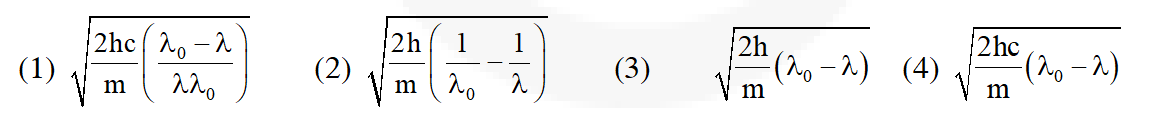[JEE-Main(online) 2014]
Ans. (1)
$\mathrm{E}=\phi+\frac{1}{2} \mathrm{mv}^{2}$
$\Rightarrow \frac{\mathrm{hc}}{\lambda}=\frac{\mathrm{hc}}{\lambda_{0}}+\frac{1}{2} \mathrm{mv}^{2}$
$\Rightarrow \mathrm{v}^{2}=\frac{2 \mathrm{hc}}{\mathrm{m}}\left[\frac{1}{\lambda}-\frac{1}{\lambda_{0}}\right] \Rightarrow \mathrm{v}=\sqrt{\frac{2 \mathrm{hc}}{\mathrm{m}}\left[\frac{1}{\lambda}-\frac{1}{\lambda_{0}}\right]}$
$\Rightarrow \mathrm{v}=\sqrt{\frac{2 \mathrm{hc}}{\mathrm{m}}\left[\frac{\lambda_{0}-\lambda}{\lambda \lambda_{0}}\right]}$
Q. Ionization energy of gaseous Na atoms is 495.5 $\mathrm{kjmol}^{-1}$ . The
lowest possible frequency of light that ionizes a sodium atom is
$\left(\mathrm{h}=6.626 \times 10^{-34} \mathrm{Js}, \mathrm{N}_{\mathrm{A}}=6.022
\times 10^{23} \mathrm{mol}^{-1}\right)$
(1) $3.15 \times 10^{15} \mathrm{s}^{-1}$
(2) $4.76 \times 10^{14} \mathrm{s}^{-1}$
(3) $1.24 \times 10^{15} \mathrm{s}^{-1}$
(4) $7.50 \times 10^{4} \mathrm{s}^{-1}$
[JEE-Main(online) 2014]
Ans. (3)
$\Delta \mathrm{E}=\mathrm{hv}$
$\mathrm{v}=\frac{\Delta \mathrm{E}}{\mathrm{h}}$
$\mathrm{v}=\frac{495.5 \times 10^{3} \mathrm{Joule}}{6.023 \times 10^{23}} \times \frac{1}{6.626 \times 10^{-34}}$
$\mathrm{v}=1.24 \times 10^{15} \mathrm{sec}^{-1}$
Q. Which of the following is the energy of a possible excited state of hydrogen?
(1) –3.4 eV (2) +6.8 eV (3) +13.6 eV (4) –6.8 eV
[JEE-Main(offline) 2015]
Ans. (1)
For H-atom, (Z = 1)
$\mathrm{E}_{\mathrm{n}}=-13.6 \times \frac{\mathrm{Z}^{2}}{\mathrm{n}^{2}} \mathrm{eV}$
$\begin{aligned} \therefore \text { So for } \mathrm{E}_{1} &=-13.6 \mathrm{eV} \\ \mathrm{E}_{2} &=-3.4 \mathrm{eV} \end{aligned}$
Q. A stream of electrons from a heated filament was passed between two charged plates kept at a potential difference V esu. If e and m are charge and mass of an electron respectively, then the value of $\mathrm{h} / \lambda$ (where $\lambda$is wavelength associated with electron wave) is given by :
(1) $\sqrt{2 \mathrm{meV}}$
(2) mev
(3) $2 \mathrm{meV}$
(4) $\sqrt{\mathrm{meV}}$
[JEE-Main 2016]
Ans. (1)
As electron of charge 'e' is passed through 'V' volt, kinetic energy of electron becomes = 'eV'
As wavelength of $e^{-}$ wave = $(\lambda)=\frac{\mathrm{h}}{\sqrt{2 \mathrm{m} \cdot \mathrm{K} \cdot \mathrm{E}}}$
$\lambda=\frac{\mathrm{h}}{\sqrt{2 \mathrm{meV}}}$
$\therefore \quad \frac{\mathrm{h}}{\lambda}=\sqrt{2 \mathrm{meV}}$
Q. The radius of the second Bohr orbit for hydrogen atom is :
(Planks const. $\mathrm{h}=6.6262 \times 10^{-34} \mathrm{Js}$; mass of electron $=9.1091 \times 10^{-31} \mathrm{kg} ;$ charge of electron $\mathrm{e}=$ $1.60210 \times 10^{-19} \mathrm{C}:$ permittivity of vaccuml $\left.\epsilon_{0}=8.854185 \times 10^{-12} \mathrm{kg}^{-1} \mathrm{m}^{-3} \mathrm{A}^{2}\right)$
[JEE-Main 2017]
[JEE-Main 2017]
Ans. (4)
Radius of $\mathbf{n}^{\mathrm{th}}$ Bohr orbit in H-atom
Radius of II Bohr orbit $=0.53 \times(2)^{2}$
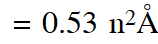Radius of II Bohr orbit $=0.53 \times(2)^{2}$
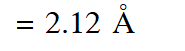
Comments
Aryan singh
May 10, 2024, 6:35 a.m.
Thank you sir but The question were too basic now jee will surely ask tougher than this so please provide some hard questions sir
..
pharmacy
Oct. 18, 2023, 7:03 a.m.
Hey there I am so excited I found your webpage, I really found you by accident, while I was researching on Askjeeve for something else, Nonetheless I am here now and would just like to say thanks a lot for a fantastic post and a all round enjoyable blog (I also love the theme/design), I don’t have time to go through it all at the minute but I have saved it and also added in your RSS feeds, so when I have time I will be back to read more, Please do keep up the fantastic jo.
Vijaya durga
May 31, 2021, 5:49 a.m.
Very useful information regarding to atomic structure I prefer esaral for this kind of solutions and questions
VAIDIK
Feb. 16, 2021, 3:58 p.m.
I LIKE THIS WEBSITE BCZ THEY PROVIDE QUESTIONS SPECIFICALLY WHICH WERE ASKED IN JEE ONLY SO DURING EXAM TIME WE CAN KNOW THAT WHAT KING OF QUESTION WILL BE GONNA ASK IN JEE