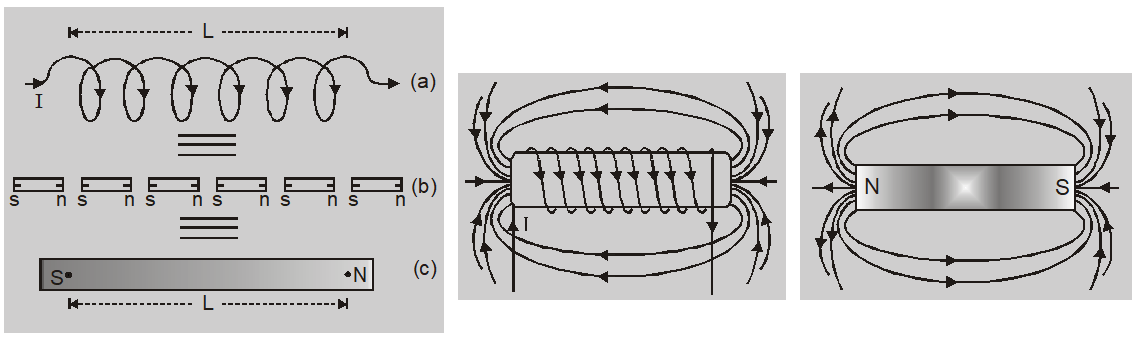
Bar Magnet as an Equivalent Solenoid - Magnetism || Class 12 Physics Notes

Bar Magnet as an Equivalent Solenoid

In solenoid each turn behaves as a small magnetic dipole having dipole moment $\mathrm{I} \mathrm{A}$. A solenoid is treated as arrangement of small magnetic dipoles placed in line with each other. The number of dipoles is equal to number of turns in a solenoid. The south and north poles of each turn cancel each other except the ends. So solenoid can be replaced by single south and north pole separated by distance equal to length of solenoid. The magnetic field produced by a bar magnet is identical to that produced by a current carrying solenoid. Derivation of Bar Magnet as an Equivalent Solenoid To demonstrate the similarity of a current carrying solenoid to a bar magnet, let us calculate axial field of a finite solenoid carrying current.

Consider: $a=$ radius of solenoid

$2 l=$ length of solenoid with centre O

$n=$ number of turns per unit length $I=$ current passing through solenoid

$O P=r$

Consider a small element of thickness $d x$ of solenoid at distance $x$ from O. and number of turns in element $=n d x$

We know magnetic field due to n turns coil at axis of solenoid is given by

$d B=\frac{\mu_{0} n d x I a^{2}}{2\left[(r-x)^{2}+a^{2}\right]^{\frac{3}{2}}}$

The magnitude of the total field is obtained by summing over all the elements $-$ in other words by integrating from $x=-1$ to $x=+1 .$ Thus,

$B=\frac{\mu_{0} n I a^{2}}{2} \int_{-1}^{l} \frac{d x}{\left[(r-x)^{2}+a^{2}\right]^{3 / 2}}$

This integration can be done by trigonometric substitutions. This exercise, however, is not necessary for our purpose. Note that the range of $x$ is from $-1$ to $+1 .$ Consider the far axial field of the solenoid, i.e., $r>>$ a and $r>>1 .$ Then the denominator is approximated by

$\begin{aligned}\left[(r-x)^{2}+a^{2}\right]^{3 / 2} &=r^{3} \\ \text { and } B &=\frac{\mu_{0} n I a^{2}}{2 r^{3}} \int_{-1}^{1} d x \\ &=\frac{\mu_{0} n I}{2} \frac{2 l a^{2}}{r^{3}} \end{aligned}$

Note that the magnitude of the magnetic moment of the solenoid is, (total number of turns $\times$ current $\times$ cross-sectional area). Thus,

$B=\frac{\mu_{0}}{4 \pi} \frac{2 m}{r^{3}}$

It is clear from the above expression that magnetic moment of a bar magnet is equal to the magnetic moment of an equivalent solenoid that produces the same magnetic field.

      Also Read: Biot Savart's Law   Click here for the Video tutorials of Magnetic Effect of Current Class 12

About eSaral At eSaral we are offering a complete platform for IIT-JEE & NEET preparation. The main mission behind eSaral is to provide education to each and every student in India by eliminating the Geographic and Economic factors, as a nation’s progress and development depends on the availability of quality education to each and every one. With the blend of education & technology, eSaral team made the learning personalized & adaptive for everyone.

For free video lectures and complete study material, Download eSaral APP.