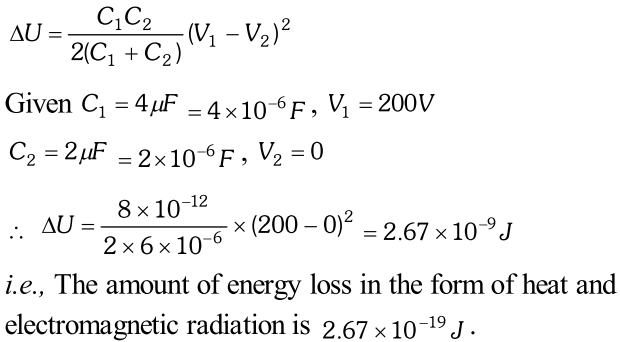Get important questions of Capacitor for Boards exams. Download or View the Physics Question Bank Class 12. These important questions will play significant role in clearing concepts of Physics. This question bank is designed by NCERT keeping in mind and the questions are updated with respect to upcoming Board exams. You will get here all the important questions for class 12 Physics chapter wise CBSE. Click Here for Detailed Chapter-wise Notes of PHYSICS for Class 12th, JEE & NEET. Q. What is the physical significance of capacitance ?
Ans. Capacitance of an arrangement tells us the potential to which the arrangement will be raised when a given charge is placed on it. For a given charge, smaller the potential large must be the capacitance and vice-versa.
Q. Show graphically the variation of charge
‘q’ with time ‘t’ when a condenser charged.
Ans. 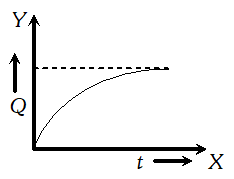
Q. What is a dielectric?
Ans. A material that does not conduct electricity but on applying electric field, induced charges are produced on its faces is called dielectric. In other words, the dielectrics have the property of transmitting electric effects without conducting.
Q. Define dielectric constant in terms of the capacitance of a capacitor.
Ans. The dielectric constant of a dielectric medium is defined as the ratio of the capacitance of the capacitor, when the dielectric fills the space between the plates to the capacitance, when there is vacuum between the two plates of the capacitor. i.e., . $K=\frac{C_{\text {medium }}}{C_{\text {air }}}$
Q. Can there be a potential difference between two conductors of same volume carrying equal positive charges?
Ans. Yes, because two conductors of same volume may have different shapes and hence difference capacitances.
Q. A capacitor of capacitance C is charged fully by connecting it to a battery of e.m.f. E. It is then disconnected from the battery. If the separation between the plates of the capacitor is now doubled,what will happen to (i) Charge stored by the capacitor. (ii) Potential difference across it. (iii) Field strength between the plates. (iv) Energy stored by the capacitor.
Ans. As battery has been disconnected, charge can neither be added nor removed. Increasing the distance to double the value will decrease the capacitance to half. Hence (i) Charge stored would be same. (ii) Potential difference $\left(=\frac{Q}{C}\right)$ would be doubled. (iii) Electric field $\left(=\frac{V}{d}\right)$ would remain same. (iv) Energy $\left(=\frac{Q^{2}}{2 C}\right)$ stored would be doubled.
Q. The battery remains connected to a parallel plate capacitor and a dielectric slab is inserted between the plates. What will be the effect on its (i) capacity (ii) charge (iii) potential difference (iv) electric field, (v) energy stored?
Ans. When battery remains connected, potential difference $V$ remains constant. Capacity $C$ increase $Q=C V$ increases. Electric field $E=\frac{E_{0}}{K}=\frac{V}{d K}$ will decrease. Energy stored $=\frac{1}{2} C V^{2}$ increases.
Q. In the above question, if battery is removed after charging the condenser and dielectric slab introduced how are all the five parameters affected?
Ans. When battery is removed, charge $Q$ remains constant, capacity $C$ increases. Potential difference $V=Q / C$ decreases. Electric field $E=\frac{V}{d}$ decreases. Energy stored $=\frac{1}{2} \frac{Q^{2}}{C}$ decreases.
Q. What will be the new capacitance of a capacitor in which a metal foil of negligible thickness is introduced between the plates.
Ans. Let us consider a capacitor of plate area
A and separation between the plates
d. Its capacity is . $C_{0}=\frac{\varepsilon_{0} A}{d}$On introducing a thin metal sheet in the middle of the plates it will act like a combination of two capacitors in series with plate area
A and plate separation $\frac{d}{2}$ . Capacity of each capacitor will be

Q. Four capacitors are connected as shown in the figure given below :
Calculate the equivalent capacitance between the points X and Y. 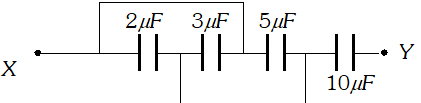
Ans. Equivalent circuit is shown in figure. Hence, capacitance for parallel combination,
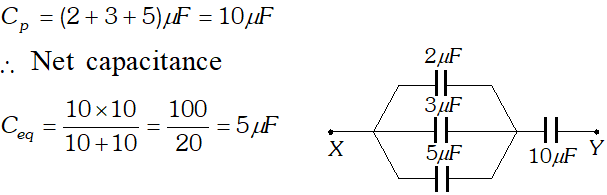
Q. A parallel plate capacitor with air between the plates has a capacitance of $8 p F \quad\left(1 p F=10^{-12} F\right)$ . What will be the capacitance if the distance between the plates is reduced by half, and the space between them is filled with a substance of dielectric constant 6 ? [NCERT]
Ans. Given $: C_{0}=8 p F=8 \times 10^{-12} F, d^{\prime}=\frac{d}{2}, K=6$ $C=K \frac{2 \in_{0} A}{d}=2 K C_{0}$ \[\Rightarrow C=2 \times 6 \times 8 \times 10^{-12} F=96 p F\] \[\]
Q. Three capacitors each of capacitance $9 p F120 V$ supply. [NCERT]
Ans. 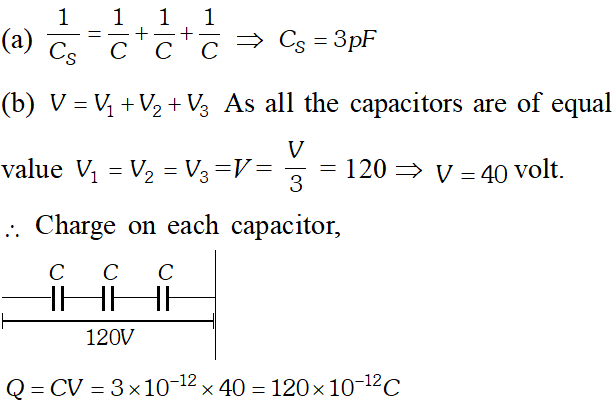
Q. In a parallel plate capacitor with air between the plates, each plates has an area of $6 \times 10^{-3}$ and the distance between the plates in 3mm. Calculate the capacitance of the capacitor. If this capacitor is connected to a 100V supply, what is the charge on each plate of the capacitor ? [NCERT]
Ans. 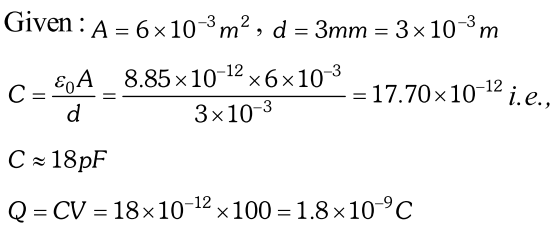
Q. Explain what would happen if in above capacitor of capacitance $18 p F$ , a 3mm thick mica sheet (of dielectric constant = 6) were inserted between the plates. (i) While the voltage supply remained connected. (ii) After the supply was disconnected. [NCERT]
Ans. Given $: C=18 p F, V=100$ volt, $t=3 m m, k=6$ (a) $C_{1}=6 \times 18 p F=108 p F$ $Q_{1}=108 \times 10^{-12} \times 100=1.08 \times 10^{-8} C, V_{1}=100 V$ (b) $Q_{2}=Q=1.8 \times 10^{-9}, C_{2}=108 p F, \quad V_{2}=\frac{100}{6}=16.6 \mathrm{V}$
Q. Find the equivalent capacitance of the combination of capacitors between the points
A and
B as shown in the figure. Also calculate the total charge that flows in the circuit when a 100
V battery is connected between the point
A and
B.
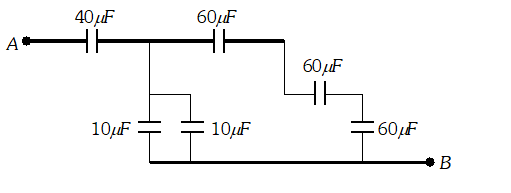
Ans. From given circuit, it is clear that capacitors of
$60 \mu F$ are in series. Their equivalent capacitance is $C_{1}=\frac{60}{3}=20 \mu F$ 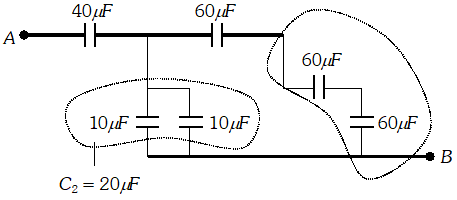 Also two capacitors of $10 \mu F$ are in parallel. Their equivalent capacitance is $C_{2}=10+10=20 \mu F . C_{1}$ and $C_{2}$ are mutually parallel, so their equivalent capacitance $C_{12}=C_{1}+C_{2}=20+20=40 \mu F$ Now $C_{12}$ and $40 \mu F$ are in series, hence equivalent capacitance of network is given by $\frac{1}{C_{A B}}=\frac{1}{C_{12}}+\frac{1}{40}=\frac{1}{40}+\frac{1}{40}=\frac{1}{20} \Rightarrow C_{A B}=20 \mu F$ Charge $Q=C V=20 \times 10^{-6} \times 100=2 \times 10^{-4} C$
Also two capacitors of $10 \mu F$ are in parallel. Their equivalent capacitance is $C_{2}=10+10=20 \mu F . C_{1}$ and $C_{2}$ are mutually parallel, so their equivalent capacitance $C_{12}=C_{1}+C_{2}=20+20=40 \mu F$ Now $C_{12}$ and $40 \mu F$ are in series, hence equivalent capacitance of network is given by $\frac{1}{C_{A B}}=\frac{1}{C_{12}}+\frac{1}{40}=\frac{1}{40}+\frac{1}{40}=\frac{1}{20} \Rightarrow C_{A B}=20 \mu F$ Charge $Q=C V=20 \times 10^{-6} \times 100=2 \times 10^{-4} C$ Q. Three identical capacitors $C_{1}, C_{2}$ and $C_{3}$ of capacitance $6 \mu F$ each are connected to a $12 V$battery as shown. Find charge on each capacitor.
[NCERT] 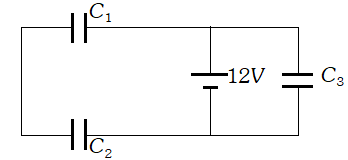
Ans. Redrawing the diagram., we get circuit as shown in figure.
Clearly $C_{3}$ is in parallel to $12 V$ source. $\Rightarrow V_{3}=12 V$ and $Q_{3}=C_{3} V=6 \times 12=72 \mu C$ i.e., $Q_{3}=72 \mu C$ Now, $C_{12}=3 \mu F$ $\Rightarrow Q_{12}=C_{12} \times V=36 \mu C$ Hence, $Q_{1}=Q_{2}=36 \mu C$ 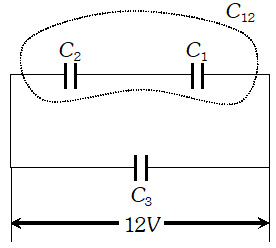
Q. A $600 p F$ capacitor is charged by a 200V supply. It is then disconnected from the supply and is connected to another uncharged capacitor. How much electrostatic energy is lost in the process? [NCERT]
Ans. 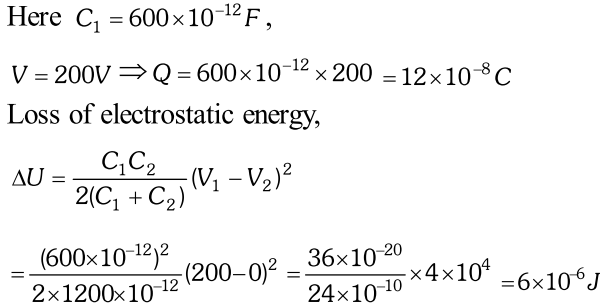
Q. The plates of a plate capacitor have an area of $90 \mathrm{cm}^{2}$ each and are separated by 2.5mm. The capacitor is charged by connecting it to a 400V supply : (i) How much electrostatic energy is stored by the capacitor? (ii) View this energy as stored in the electrostatic field between the plates, and obtain the energy per unit volume u. [NCERT]
Ans. 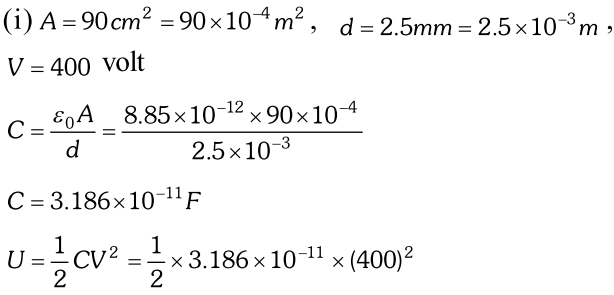
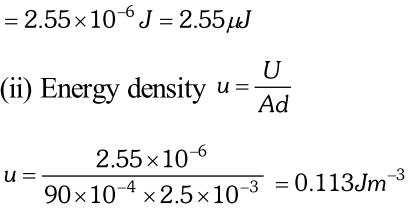
Q. A $4 \mu F$ capacitor is charged by a 200V supply. It is then disconnected from the supply, and is connected to another uncharged $2 \mu \mathrm{F}$ capacitor. How much electrostatic energy of the first capacitor is lost in the form of heat and electromagnetic radiation ? [NCERT]
Ans. 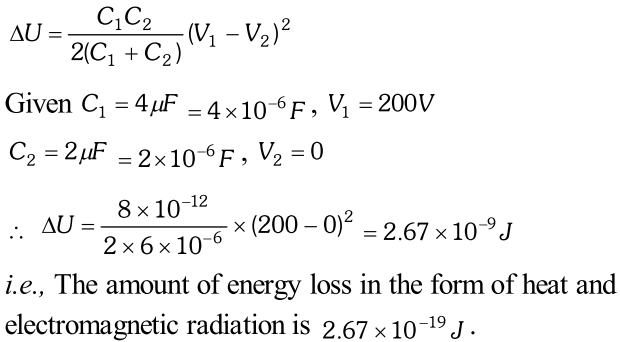
Q. A parallel plate capacitor is to be designed with a voltage rating $1 k V$, using a material of dielectric constant 3 and dielectric strength about $10^{7} \mathrm{Vm}^{-1}$ . (Dielectric strength is the maximum electric field a material can tolerate without breakdown, i.e., without starting to conduct electricity through partial ionisation) for safety, we should like the field never to exceed, say 10% of the dielectric strength. What minimum area of the plates is required to have a capacitance of $50 p F$ ? [NCERT]
Ans. Capacitance of proposed capacitor $=50 \mu F,$ Dielectric
strength $=10^{7} \mathrm{Vm}^{-1}$ and $K=3$ $\therefore$ Electric field to be established $=10^{7} \times \frac{10}{100}=10^{6} \mathrm{Vm}^{-1}$ Voltage rating $=1 \mathrm{kV}, \mathrm{V}=\mathrm{E} d, \quad d=$ thickness of dielectric slab. $\therefore$ Minimum thickness of dielectric slab is 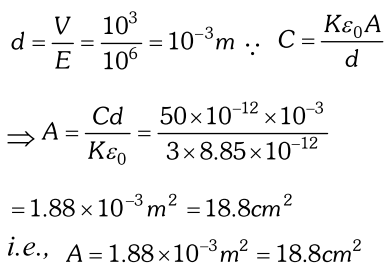
Q. The given graph shows the variation of charge $q$ versus potential difference $V$ for two capacitors $C_{1}$ and $C_{2} .$The two capacitors have same plate separation but the plate area of $C_{2}$ is double than that of $C_{1} .$ Which of the lines in the graph correspond to and and why?
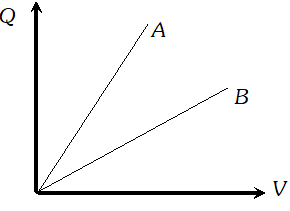
Ans. As $q=\frac{C}{V},$ and graph $A$ has a larger slope than $B,$ so the graph $A$ represents a capacitor $|$ of larger capacitance. Also $C=\frac{\varepsilon_{0} A}{d} \Rightarrow C \propto A .$ As the plate area of $C_{2}$ is double that of $C_{1},$ so has a larger capacitance. Hence the line $A$ of the graph corresponds to
Q. Two charged conductors of capacitance $C_{1}$ and $C_{2}$ having potentials $V_{1}$ and $V_{2}$ respectively are connected by a conducting wire. Calculate the common potential and loss of energy in connection.
Q. (i) Derive the expression for the force between plates of a parallel plate capacitor. (ii) Show that the force on each plate of a parallel plate capacitor has magnitude equal to $\left(\frac{1}{2}\right) Q E$, where Q is the charge on the capacitor, and E is magnitude of electric field between the plates. Explain the origin of the factor $\frac{1}{2}$ . [NCERT]
Ans. (i) Consider a parallel plate capacitor with plate area
A. Suppose a positive charge is given to one plate and a negative charge to the other plate. The electric field due to only the positive plate is
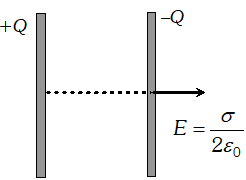 $E_{+}=\frac{\sigma}{2 \varepsilon_{0}}=\frac{Q}{2 A \varepsilon_{0}}$ at all points if the plate is large. The negative charge $-Q$ finds itself in the field of this positive charge. The force $-Q$ on is, therefore $\cdot F=-Q E$$=(-Q) \frac{Q}{2 A \varepsilon_{0}}=-\frac{Q^{2}}{2 A \varepsilon_{0}}$ The magnitude of the force is is $F=\frac{Q^{2}}{2 A \varepsilon_{0}}$ (ii) Work done in increasing the separation between the plates by a distance $d x$ against the force of attraction $F$ between the plates is $d W=F d x \cdots$ (i) As, energy density, $u=\frac{1}{2} \varepsilon_{0} E^{2}$ $\therefore$ Increase in potential energy m $=u A d x=\frac{1}{2} \varepsilon_{0} E^{2} A d x \ldots$ (ii) From the equation (i) and (ii)
$E_{+}=\frac{\sigma}{2 \varepsilon_{0}}=\frac{Q}{2 A \varepsilon_{0}}$ at all points if the plate is large. The negative charge $-Q$ finds itself in the field of this positive charge. The force $-Q$ on is, therefore $\cdot F=-Q E$$=(-Q) \frac{Q}{2 A \varepsilon_{0}}=-\frac{Q^{2}}{2 A \varepsilon_{0}}$ The magnitude of the force is is $F=\frac{Q^{2}}{2 A \varepsilon_{0}}$ (ii) Work done in increasing the separation between the plates by a distance $d x$ against the force of attraction $F$ between the plates is $d W=F d x \cdots$ (i) As, energy density, $u=\frac{1}{2} \varepsilon_{0} E^{2}$ $\therefore$ Increase in potential energy m $=u A d x=\frac{1}{2} \varepsilon_{0} E^{2} A d x \ldots$ (ii) From the equation (i) and (ii) 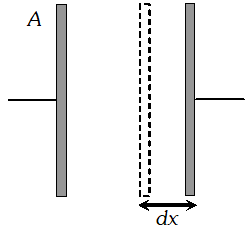 $F d x=\frac{1}{2} \varepsilon_{0} E^{2} A d x \Rightarrow F=\frac{1}{2} \varepsilon_{0} E^{2} A=\frac{1}{2}\left(\varepsilon_{0} A E\right) E$ $\Rightarrow F=\frac{1}{2}\left(\varepsilon_{0} A \frac{V}{d}\right) E \Rightarrow F=\frac{1}{2}(C V) E \Rightarrow F=\frac{1}{2} Q E$ The factor $\frac{1}{2}$ is in the expression due to the fact that plates are being moved against an average value $\frac{E}{2} .$
$F d x=\frac{1}{2} \varepsilon_{0} E^{2} A d x \Rightarrow F=\frac{1}{2} \varepsilon_{0} E^{2} A=\frac{1}{2}\left(\varepsilon_{0} A E\right) E$ $\Rightarrow F=\frac{1}{2}\left(\varepsilon_{0} A \frac{V}{d}\right) E \Rightarrow F=\frac{1}{2}(C V) E \Rightarrow F=\frac{1}{2} Q E$ The factor $\frac{1}{2}$ is in the expression due to the fact that plates are being moved against an average value $\frac{E}{2} .$ Q. A conducting slab of thickness $t$ ' is introduced without touching between the plates of a parallel plate capacitor, separated by a distance 'd' $(t
Ans. Let $\sigma$ be the surface charge density on capacitor plates of area $A$ Electric field between the air space is $E=\frac{\sigma}{\varepsilon_{0}}$
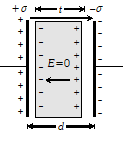 As in case of conducting slab $E_{i}=E_{0} .$ (Net electricfield inside the conducting slab is zero $) .$ Now potential, difference between the plates of capacitor is $V=E_{0}(d-t)=\frac{\sigma}{\varepsilon_{0}}(d-t)$$\Rightarrow Q=\sigma A \Rightarrow C=\frac{Q}{V}=\frac{\varepsilon_{0} A}{d-t}$
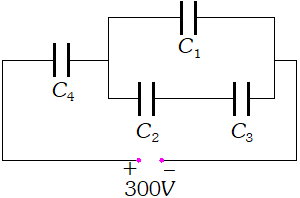
As in case of conducting slab $E_{i}=E_{0} .$ (Net electricfield inside the conducting slab is zero $) .$ Now potential, difference between the plates of capacitor is $V=E_{0}(d-t)=\frac{\sigma}{\varepsilon_{0}}(d-t)$$\Rightarrow Q=\sigma A \Rightarrow C=\frac{Q}{V}=\frac{\varepsilon_{0} A}{d-t}$ Q. Obtain the equivalent capacitance for the following network.
For a $300 V$ supply, determine the charge and voltage across each capacitor 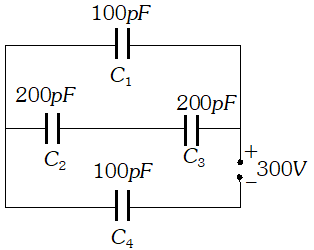
Click Here for Detailed Notes of any chapter.
eSaral provides you complete edge to prepare for Board and Competitive Exams like JEE, NEET, BITSAT, etc. We have transformed classroom in such a way that a student can study anytime anywhere. With the help of AI we have made the learning Personalized, adaptive and accessible for each and every one. Visit eSaral Website to download or view free study material for JEE & NEET. Also get to know about the strategies to Crack Exam in limited time period.


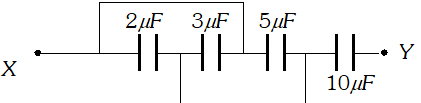
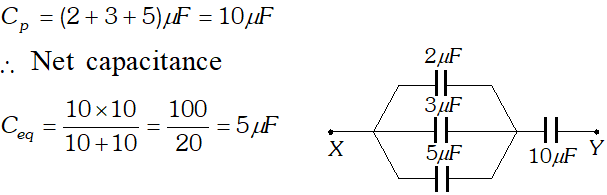
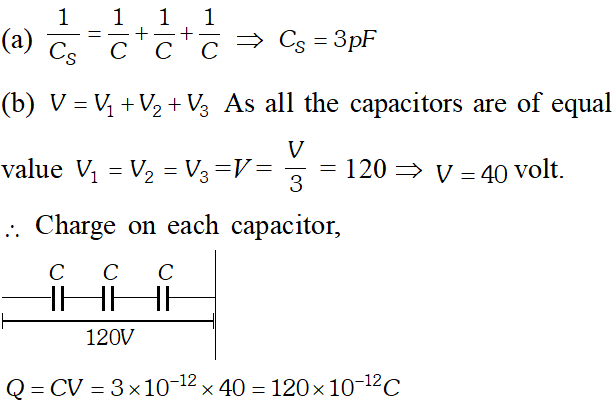
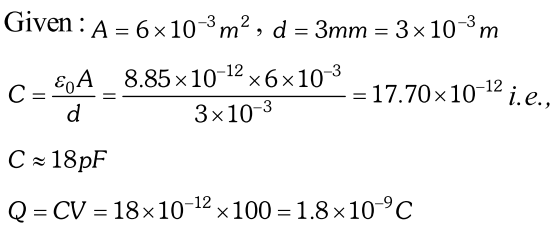

 Also two capacitors of $10 \mu F$ are in parallel. Their equivalent capacitance is $C_{2}=10+10=20 \mu F . C_{1}$ and $C_{2}$ are mutually parallel, so their equivalent capacitance $C_{12}=C_{1}+C_{2}=20+20=40 \mu F$ Now $C_{12}$ and $40 \mu F$ are in series, hence equivalent capacitance of network is given by $\frac{1}{C_{A B}}=\frac{1}{C_{12}}+\frac{1}{40}=\frac{1}{40}+\frac{1}{40}=\frac{1}{20} \Rightarrow C_{A B}=20 \mu F$ Charge $Q=C V=20 \times 10^{-6} \times 100=2 \times 10^{-4} C$
Also two capacitors of $10 \mu F$ are in parallel. Their equivalent capacitance is $C_{2}=10+10=20 \mu F . C_{1}$ and $C_{2}$ are mutually parallel, so their equivalent capacitance $C_{12}=C_{1}+C_{2}=20+20=40 \mu F$ Now $C_{12}$ and $40 \mu F$ are in series, hence equivalent capacitance of network is given by $\frac{1}{C_{A B}}=\frac{1}{C_{12}}+\frac{1}{40}=\frac{1}{40}+\frac{1}{40}=\frac{1}{20} \Rightarrow C_{A B}=20 \mu F$ Charge $Q=C V=20 \times 10^{-6} \times 100=2 \times 10^{-4} C$ 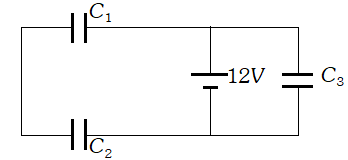

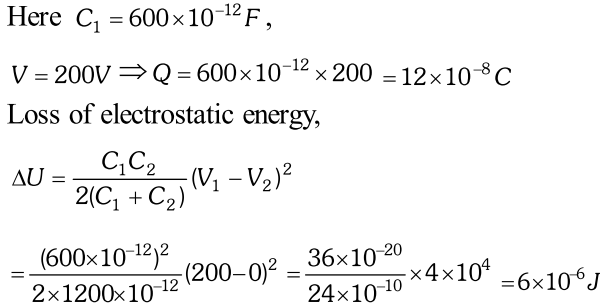
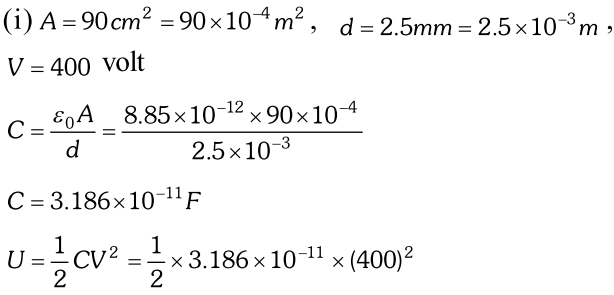
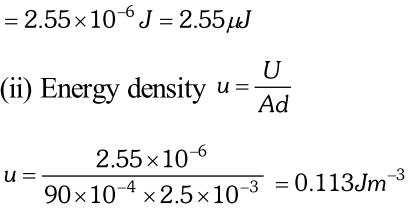
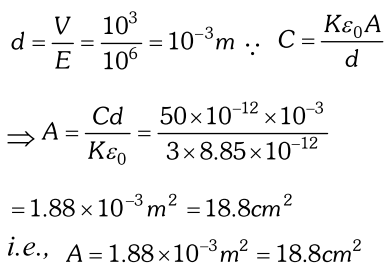

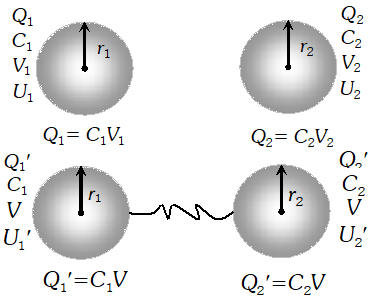 $\therefore$ Total charge, $Q=Q_{1}+Q_{2} \ldots(i)$ But $Q_{1}=C_{1} V_{1}$ and $Q_{2}=C_{2} V_{2}$ $\therefore$ By equation (i) we get $Q=C_{1} V_{1}+C_{2} V_{2}$ Total capacity $C=C_{1}+C_{2}$ (i) Common potential: Let the conductors are connected by a wire and the common potential becomes $V$.
$\therefore$ Total charge, $Q=Q_{1}+Q_{2} \ldots(i)$ But $Q_{1}=C_{1} V_{1}$ and $Q_{2}=C_{2} V_{2}$ $\therefore$ By equation (i) we get $Q=C_{1} V_{1}+C_{2} V_{2}$ Total capacity $C=C_{1}+C_{2}$ (i) Common potential: Let the conductors are connected by a wire and the common potential becomes $V$. 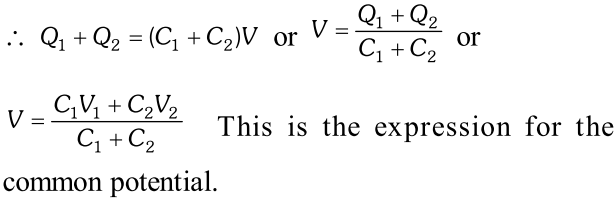 (ii) Loss of Energy: Total energy of the conductors before connection
(ii) Loss of Energy: Total energy of the conductors before connection 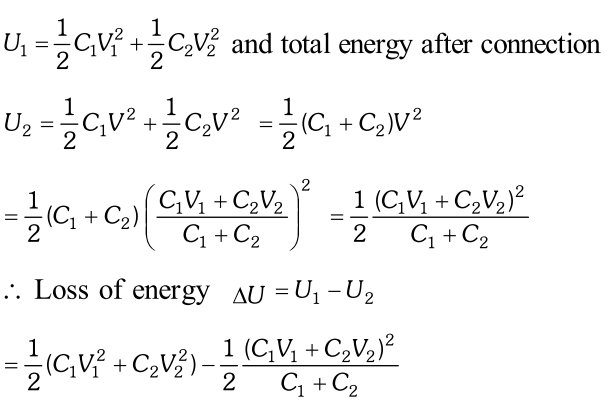 since is always positive therefore will be always positive. Hence in the distribution of charges there is always a loss of energy. $\therefore$ Loss energy
since is always positive therefore will be always positive. Hence in the distribution of charges there is always a loss of energy. $\therefore$ Loss energy  $E_{+}=\frac{\sigma}{2 \varepsilon_{0}}=\frac{Q}{2 A \varepsilon_{0}}$ at all points if the plate is large. The negative charge $-Q$ finds itself in the field of this positive charge. The force $-Q$ on is, therefore $\cdot F=-Q E$$=(-Q) \frac{Q}{2 A \varepsilon_{0}}=-\frac{Q^{2}}{2 A \varepsilon_{0}}$ The magnitude of the force is is $F=\frac{Q^{2}}{2 A \varepsilon_{0}}$ (ii) Work done in increasing the separation between the plates by a distance $d x$ against the force of attraction $F$ between the plates is $d W=F d x \cdots$ (i) As, energy density, $u=\frac{1}{2} \varepsilon_{0} E^{2}$ $\therefore$ Increase in potential energy m $=u A d x=\frac{1}{2} \varepsilon_{0} E^{2} A d x \ldots$ (ii) From the equation (i) and (ii)
$E_{+}=\frac{\sigma}{2 \varepsilon_{0}}=\frac{Q}{2 A \varepsilon_{0}}$ at all points if the plate is large. The negative charge $-Q$ finds itself in the field of this positive charge. The force $-Q$ on is, therefore $\cdot F=-Q E$$=(-Q) \frac{Q}{2 A \varepsilon_{0}}=-\frac{Q^{2}}{2 A \varepsilon_{0}}$ The magnitude of the force is is $F=\frac{Q^{2}}{2 A \varepsilon_{0}}$ (ii) Work done in increasing the separation between the plates by a distance $d x$ against the force of attraction $F$ between the plates is $d W=F d x \cdots$ (i) As, energy density, $u=\frac{1}{2} \varepsilon_{0} E^{2}$ $\therefore$ Increase in potential energy m $=u A d x=\frac{1}{2} \varepsilon_{0} E^{2} A d x \ldots$ (ii) From the equation (i) and (ii)  $F d x=\frac{1}{2} \varepsilon_{0} E^{2} A d x \Rightarrow F=\frac{1}{2} \varepsilon_{0} E^{2} A=\frac{1}{2}\left(\varepsilon_{0} A E\right) E$ $\Rightarrow F=\frac{1}{2}\left(\varepsilon_{0} A \frac{V}{d}\right) E \Rightarrow F=\frac{1}{2}(C V) E \Rightarrow F=\frac{1}{2} Q E$ The factor $\frac{1}{2}$ is in the expression due to the fact that plates are being moved against an average value $\frac{E}{2} .$
$F d x=\frac{1}{2} \varepsilon_{0} E^{2} A d x \Rightarrow F=\frac{1}{2} \varepsilon_{0} E^{2} A=\frac{1}{2}\left(\varepsilon_{0} A E\right) E$ $\Rightarrow F=\frac{1}{2}\left(\varepsilon_{0} A \frac{V}{d}\right) E \Rightarrow F=\frac{1}{2}(C V) E \Rightarrow F=\frac{1}{2} Q E$ The factor $\frac{1}{2}$ is in the expression due to the fact that plates are being moved against an average value $\frac{E}{2} .$  As in case of conducting slab $E_{i}=E_{0} .$ (Net electricfield inside the conducting slab is zero $) .$ Now potential, difference between the plates of capacitor is $V=E_{0}(d-t)=\frac{\sigma}{\varepsilon_{0}}(d-t)$$\Rightarrow Q=\sigma A \Rightarrow C=\frac{Q}{V}=\frac{\varepsilon_{0} A}{d-t}$
As in case of conducting slab $E_{i}=E_{0} .$ (Net electricfield inside the conducting slab is zero $) .$ Now potential, difference between the plates of capacitor is $V=E_{0}(d-t)=\frac{\sigma}{\varepsilon_{0}}(d-t)$$\Rightarrow Q=\sigma A \Rightarrow C=\frac{Q}{V}=\frac{\varepsilon_{0} A}{d-t}$ 
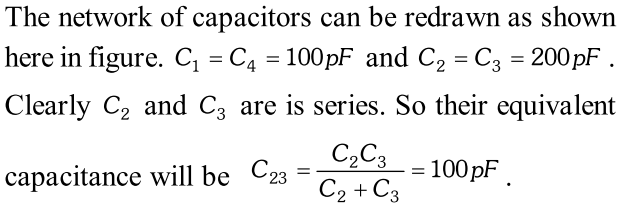
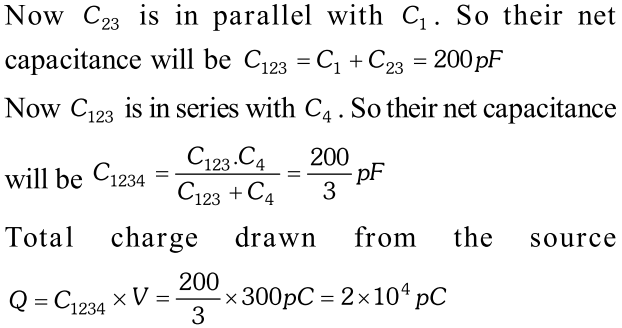
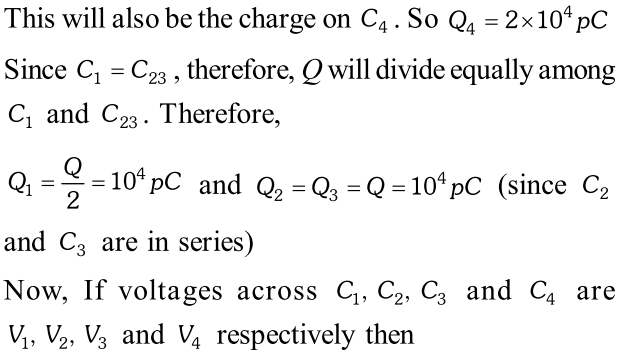
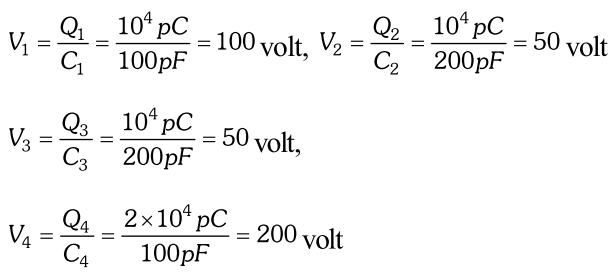 \
\