eSaral provides chemistry short notes for JEE and NEET to help students in revising topics quickly. These notes are completely based on latest syllabus and it includes all the tips and tricks that will help you in learning chemistry better and score well.
The Notes will help you to understand the important topics and remember the key points for exam point of view.
You can also access detailed Notes of chemistry here.
Download or View Detailed Notes for Chemistry Class 11th
Download or View Detailed Notes for Chemistry Class 12th
CHEMISTRY
CHEMICAL KINETICS
THEORY
It is a branch of physical chemistry deals with the "Rate of Chemical Reactions" including the effect of temperature, pressure, concentration, etc., on the rates, and the mechanism by which the reaction takes place.
Rate of chemical Reaction is defined as the change in concentration of a reactant (or a product) in a particular time interval. Average rate of reaction, Instantaneous rate of reaction.
Units of Reaction Rate are unit of concentration divided by the unit of time $\left(\mathrm{mol} \mathrm{L}^{-1} \mathrm{s}^{-1} \text { or } \mathrm{mol} \mathrm{L}^{-1} \mathrm{min}^{-1} \text { or so on }\right)$
Factors Affecting Reaction Rates :
(i) Concentration of reactants and
(ii) Reaction temperature
Besides these, presence of catalyst and surface area (if a reactant or a catalyst is a solid) exposure to radiation also affect the reaction rates.
Expressions or the rate :
For a general reaction $: a A+b B \longrightarrow c C+d D$
The rate of disappearance of A $=-\frac{\mathrm{d}[\mathrm{A}]}{\mathrm{dt}}$; Rate of disappearance of B $=-\frac{\mathrm{d}[\mathrm{B}]}{\mathrm{dt}}$ ;
Rate of appearance of C = $\frac{\mathrm{d}[\mathrm{C}]}{\mathrm{dt}}$ & Rate of appearance of D = $\frac{\mathrm{d}[\mathrm{D}]}{\mathrm{dt}}$.
The positive sign shows that concentrations of C and D increases with time and the negative sign indicating that concentrations of A and B decrease with time.Thus the rate of general reaction.
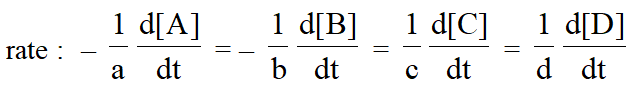 Rate Equation and Rate constant :
An expression which relates the rate of a reaction to the concentration of the reactants is called the Rate Equation or Rate Law. Rate $\propto[\mathrm{A}]^{\mathrm{a}} \cdot[\mathrm{B}]^{\mathrm{b}}$ or Rate = Rate $=\mathrm{k}[\mathrm{A}]^{\mathrm{a}}[\mathrm{B}]^{\mathrm{b}}$ . The constant of proportionality, k is known as the Rate Constant (specific reaction rate) and may be defined as the rate at unit concentrations of the reactants. k depends on the temperature and is independent of the initial concentrations of the reactants. At a fixed temperature, k is constant characteristic of the reaction. Larger value of k indicates fast reaction and small k indicates slow reactions.
Molecularity :
Molecularity of a reaction is defined as the numbers of particles (atoms, ions, groups or molecules) of reactants actually taking part in a single step chemical reaction.
Molecularity of a reaction is :
(i) Always a whole number (not zero) and never a fraction.
(ii) The value of molecularity of a simple or one step reaction does not exceed 3.
Order of Reaction :
It is defined as the sum of the exponents (powers) of the molar concentrations of the reactants in the experimentally determined rate equations.
If rate of reaction a $[\mathrm{A}]^{\mathrm{p}}[\mathrm{B}]^{\mathrm{q}}[\mathrm{C}]^{\mathrm{r}}$ or Rate of reaction $=\mathrm{k}[\mathrm{A}]^{\mathrm{p}}[\mathrm{B}]^{\mathrm{q}}[\mathrm{C}]^{\mathrm{r}}$
order of reaction = p + q + r & the order w.r.t. A, B & C are p, q & r respectively.
For a "Reaction of nth order", the order of the reaction is n and the rate equation (or Rate law) is rate $\propto[\mathrm{A}]^{\mathrm{n}}=\mathrm{k}[\mathrm{A}]^{\mathrm{n}}$
The order of a reaction is obtained from the experimentally determined rate (and not from the stoichiometric equation) and may be zero, an integer or a fraction and never exceeds 3. In a multi-step complex reaction, the order of the reaction depends on the slowest step.
Zero order reaction :
A reaction is said to be of zero order if the rate is independent of the concentration of the reactants.
$A \longrightarrow$ products $;$ Rate $\alpha \mathrm{k}[\mathrm{A}]^{\circ}=\mathrm{k} \operatorname{mol} \mathrm{L}^{-1} \mathrm{s}^{-1}$
Examples :
(i) $\quad \mathrm{H}_{2}(\mathrm{g})+\mathrm{Cl}_{2}(\mathrm{g}) \stackrel{\mathrm{hv}}{\longrightarrow} 2 \mathrm{HCl}(\mathrm{g})$
(ii) $\quad \mathrm{N}_{2} \mathrm{O}(\mathrm{g}) \frac{\text { hot Pt. }}{\text { Surface }} \mathrm{N}_{2}(\mathrm{g})+\frac{1}{2} \mathrm{O}_{2}(\mathrm{g})$
(iii) $2 \mathrm{NH}_{3}$ (g) $\frac{\text { Mo or } \mathrm{W}}{\text { surface }} \mathrm{N}_{2}+3 \mathrm{H}_{2}$
(iv) $\quad 2 \mathrm{HI}(\mathrm{g}) \frac{\mathrm{Au}}{\text { surface }} \mathrm{H}_{2}(\mathrm{g})+\mathrm{I}_{2}(\mathrm{g})$
Characteristics of Zero Order Reaction :
(1)Concentration of reactant decreases lineraly with time. $[\mathrm{A}]_{\mathrm{t}}=[\mathrm{A}]_{0}-\mathrm{kt}$
(2) Units of k are, mol $l^{-1} \operatorname{time}^{-1}$
(3) Time required for the completion of reaction t = $\frac{[\mathrm{A}]_{0}}{\mathrm{k}} \& \mathrm{t}_{1 / 2}=\frac{0.5[\mathrm{A}]_{0}}{\mathrm{k}}$
First order reaction :
a reaction is said to be of first order if its rate is proportinal to the concentration of one reactant only.
Rate Equation and Rate constant :
An expression which relates the rate of a reaction to the concentration of the reactants is called the Rate Equation or Rate Law. Rate $\propto[\mathrm{A}]^{\mathrm{a}} \cdot[\mathrm{B}]^{\mathrm{b}}$ or Rate = Rate $=\mathrm{k}[\mathrm{A}]^{\mathrm{a}}[\mathrm{B}]^{\mathrm{b}}$ . The constant of proportionality, k is known as the Rate Constant (specific reaction rate) and may be defined as the rate at unit concentrations of the reactants. k depends on the temperature and is independent of the initial concentrations of the reactants. At a fixed temperature, k is constant characteristic of the reaction. Larger value of k indicates fast reaction and small k indicates slow reactions.
Molecularity :
Molecularity of a reaction is defined as the numbers of particles (atoms, ions, groups or molecules) of reactants actually taking part in a single step chemical reaction.
Molecularity of a reaction is :
(i) Always a whole number (not zero) and never a fraction.
(ii) The value of molecularity of a simple or one step reaction does not exceed 3.
Order of Reaction :
It is defined as the sum of the exponents (powers) of the molar concentrations of the reactants in the experimentally determined rate equations.
If rate of reaction a $[\mathrm{A}]^{\mathrm{p}}[\mathrm{B}]^{\mathrm{q}}[\mathrm{C}]^{\mathrm{r}}$ or Rate of reaction $=\mathrm{k}[\mathrm{A}]^{\mathrm{p}}[\mathrm{B}]^{\mathrm{q}}[\mathrm{C}]^{\mathrm{r}}$
order of reaction = p + q + r & the order w.r.t. A, B & C are p, q & r respectively.
For a "Reaction of nth order", the order of the reaction is n and the rate equation (or Rate law) is rate $\propto[\mathrm{A}]^{\mathrm{n}}=\mathrm{k}[\mathrm{A}]^{\mathrm{n}}$
The order of a reaction is obtained from the experimentally determined rate (and not from the stoichiometric equation) and may be zero, an integer or a fraction and never exceeds 3. In a multi-step complex reaction, the order of the reaction depends on the slowest step.
Zero order reaction :
A reaction is said to be of zero order if the rate is independent of the concentration of the reactants.
$A \longrightarrow$ products $;$ Rate $\alpha \mathrm{k}[\mathrm{A}]^{\circ}=\mathrm{k} \operatorname{mol} \mathrm{L}^{-1} \mathrm{s}^{-1}$
Examples :
(i) $\quad \mathrm{H}_{2}(\mathrm{g})+\mathrm{Cl}_{2}(\mathrm{g}) \stackrel{\mathrm{hv}}{\longrightarrow} 2 \mathrm{HCl}(\mathrm{g})$
(ii) $\quad \mathrm{N}_{2} \mathrm{O}(\mathrm{g}) \frac{\text { hot Pt. }}{\text { Surface }} \mathrm{N}_{2}(\mathrm{g})+\frac{1}{2} \mathrm{O}_{2}(\mathrm{g})$
(iii) $2 \mathrm{NH}_{3}$ (g) $\frac{\text { Mo or } \mathrm{W}}{\text { surface }} \mathrm{N}_{2}+3 \mathrm{H}_{2}$
(iv) $\quad 2 \mathrm{HI}(\mathrm{g}) \frac{\mathrm{Au}}{\text { surface }} \mathrm{H}_{2}(\mathrm{g})+\mathrm{I}_{2}(\mathrm{g})$
Characteristics of Zero Order Reaction :
(1)Concentration of reactant decreases lineraly with time. $[\mathrm{A}]_{\mathrm{t}}=[\mathrm{A}]_{0}-\mathrm{kt}$
(2) Units of k are, mol $l^{-1} \operatorname{time}^{-1}$
(3) Time required for the completion of reaction t = $\frac{[\mathrm{A}]_{0}}{\mathrm{k}} \& \mathrm{t}_{1 / 2}=\frac{0.5[\mathrm{A}]_{0}}{\mathrm{k}}$
First order reaction :
a reaction is said to be of first order if its rate is proportinal to the concentration of one reactant only.
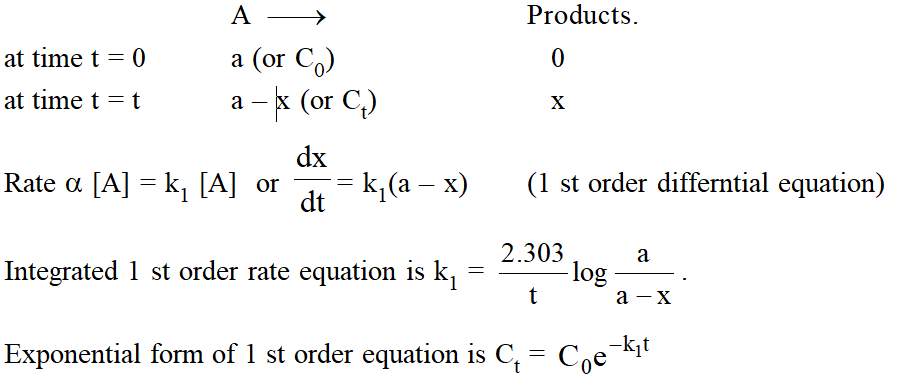 Characteristics Of First Order Reaction :
Characteristics Of First Order Reaction :
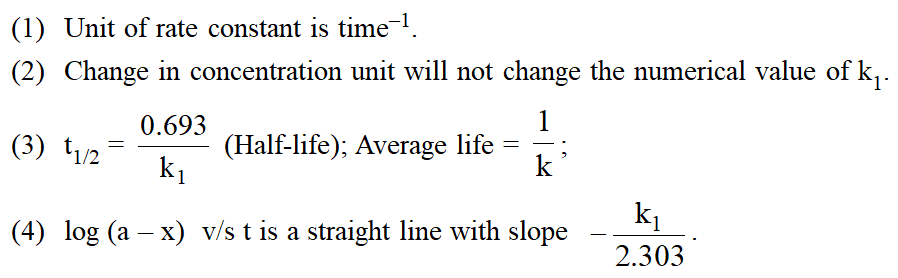 Examples :
(i) Radioactive disintegration is a first order reaction.
Examples :
(i) Radioactive disintegration is a first order reaction.
 (iii) Mineral acid catalyzed hydrolysis of esters.
(iv) Decomposition of $H_{2} O_{2}$ in aqueous solution.
Second Order Reaction :
(i) When two molecules of the same reactant are involved or the concentrations of the both reactants are equal reactions $2 \mathrm{A} \longrightarrow$ products or $\mathrm{A}+\mathrm{B} \longrightarrow$ products.
(iii) Mineral acid catalyzed hydrolysis of esters.
(iv) Decomposition of $H_{2} O_{2}$ in aqueous solution.
Second Order Reaction :
(i) When two molecules of the same reactant are involved or the concentrations of the both reactants are equal reactions $2 \mathrm{A} \longrightarrow$ products or $\mathrm{A}+\mathrm{B} \longrightarrow$ products.
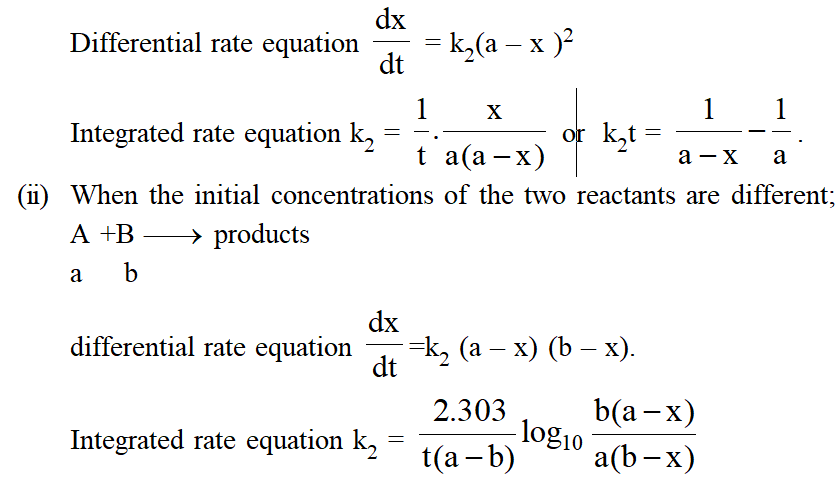 Characteristics of Second Order Reaction :
(i) Unit of rate constant L $\mathrm{mol}^{-1}$ time $^{-1}$
(ii) Numerical value of k will depend upon unit of concentration.
(iii) $\left.\mathrm{t}_{1 / 2} \propto \mathrm{a}^{-1} \text { (In general } \mathrm{t}_{1 / 2} \alpha \mathrm{a}^{(1-\mathrm{n})} ; \mathrm{n}=\text { order of reactions }\right)$
(iv) 2nd order reaction conforms to first order when one of the reactant in excess.
Examples :
Characteristics of Second Order Reaction :
(i) Unit of rate constant L $\mathrm{mol}^{-1}$ time $^{-1}$
(ii) Numerical value of k will depend upon unit of concentration.
(iii) $\left.\mathrm{t}_{1 / 2} \propto \mathrm{a}^{-1} \text { (In general } \mathrm{t}_{1 / 2} \alpha \mathrm{a}^{(1-\mathrm{n})} ; \mathrm{n}=\text { order of reactions }\right)$
(iv) 2nd order reaction conforms to first order when one of the reactant in excess.
Examples :
 Side or concurent reaction :
Side or concurent reaction :
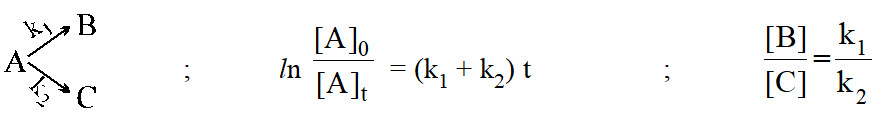 Consecutive reaction :
Consecutive reaction :
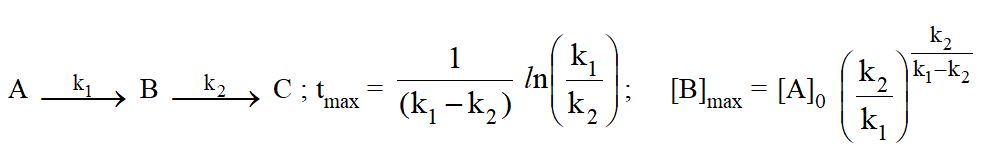 Threshold Energy and Activation Energy :
For a reaction to take place the reacting molecules must colloid together, but only those collisions, in which colliding molecules possess certain minimum energy is called threshold energy $\left(\mathrm{E}_{\mathrm{T}}\right)$.
Activation Energy $\left(\mathbf{E}_{\mathbf{a}}\right):$
The extra energy needed for the reactant molecules to be able to react chemically is known as Activation energy.
Threshold Energy and Activation Energy :
For a reaction to take place the reacting molecules must colloid together, but only those collisions, in which colliding molecules possess certain minimum energy is called threshold energy $\left(\mathrm{E}_{\mathrm{T}}\right)$.
Activation Energy $\left(\mathbf{E}_{\mathbf{a}}\right):$
The extra energy needed for the reactant molecules to be able to react chemically is known as Activation energy.
 Influence of Temperature on reaction rates :
Temperature coefficient :
The temperature coefficient of a chemical reaction is defined as the ratio of the reaction rates at two temperatures differing by $10^{\circ} \mathrm{C}$. Its value usually lies between 2 & 3.
Temperature coefficient $=\frac{\mathrm{k}_{\mathrm{t}+10}}{\mathrm{k}_{\mathrm{t}}}$
Arrhenius Equation :
Influence of Temperature on reaction rates :
Temperature coefficient :
The temperature coefficient of a chemical reaction is defined as the ratio of the reaction rates at two temperatures differing by $10^{\circ} \mathrm{C}$. Its value usually lies between 2 & 3.
Temperature coefficient $=\frac{\mathrm{k}_{\mathrm{t}+10}}{\mathrm{k}_{\mathrm{t}}}$
Arrhenius Equation :

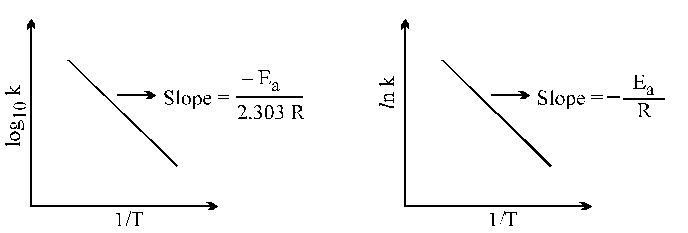
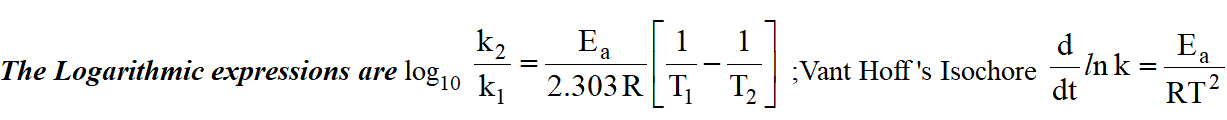 Graphical representations are :
Graphical representations are :
 Methods of Determination of order of reactions :
A few methods commonly used are given below :
1. Hit & Trial Method : It is method of using integrated rate equations, where the experimental values of a, x & t are put into these equations. One which gives a constant value of k for different sets of a, x & t correspond to the order of the reaction.
2. Graphical Method :
(i) A plot of log (a – x) versus 't' gives a straight lines for the First order reaction.
(ii) A plot of (a – x)– (n–1) versus 't' gives a straight line any reaction of the order n (except n = 1)
3.Half Life Method : The half life of different order of reactions is given by $\mathrm{a}_{\mathrm{n}}=\left(\frac{1}{2}\right)^{\mathrm{n}} \mathrm{a}_{0}$
By experimental observation of the dependence of half life on initial concentration we can determine n, the order of reaction. N $=1+\frac{\log \mathrm{t}_{2}-\log \mathrm{t}_{1}}{\log \mathrm{a}_{1}-\log \mathrm{a}_{2}}$
4. Initial rate method. Initial rate method is used to determine the order or reaction in cases where more than one reactant is used. It involves the determination of the order of different reactants separately. A series of experiments are performed in which concentration of one particular reactant is varied whereas conc. of other reactants are kept constant. In each experiment the initial rate is determined from the plot of conc. vs. time, e.g., if conc. of A is doubled, and initial rate of reaction is also doubled, order of reaction is l.
Mechanism Of reactions :
The path way which reactants are converted into the products is called the reaction mechanism. It should be clear that experimentally determined rate expression cannot be predicted from the stiochiometry of the reaction. For example for the reaction ;
Methods of Determination of order of reactions :
A few methods commonly used are given below :
1. Hit & Trial Method : It is method of using integrated rate equations, where the experimental values of a, x & t are put into these equations. One which gives a constant value of k for different sets of a, x & t correspond to the order of the reaction.
2. Graphical Method :
(i) A plot of log (a – x) versus 't' gives a straight lines for the First order reaction.
(ii) A plot of (a – x)– (n–1) versus 't' gives a straight line any reaction of the order n (except n = 1)
3.Half Life Method : The half life of different order of reactions is given by $\mathrm{a}_{\mathrm{n}}=\left(\frac{1}{2}\right)^{\mathrm{n}} \mathrm{a}_{0}$
By experimental observation of the dependence of half life on initial concentration we can determine n, the order of reaction. N $=1+\frac{\log \mathrm{t}_{2}-\log \mathrm{t}_{1}}{\log \mathrm{a}_{1}-\log \mathrm{a}_{2}}$
4. Initial rate method. Initial rate method is used to determine the order or reaction in cases where more than one reactant is used. It involves the determination of the order of different reactants separately. A series of experiments are performed in which concentration of one particular reactant is varied whereas conc. of other reactants are kept constant. In each experiment the initial rate is determined from the plot of conc. vs. time, e.g., if conc. of A is doubled, and initial rate of reaction is also doubled, order of reaction is l.
Mechanism Of reactions :
The path way which reactants are converted into the products is called the reaction mechanism. It should be clear that experimentally determined rate expression cannot be predicted from the stiochiometry of the reaction. For example for the reaction ;
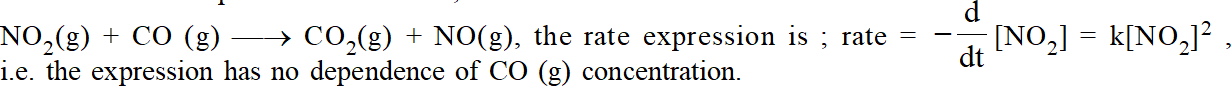 The reason is that the reaction occurs by a series of elementary steps.
The sequence of elementary processes leading to the overall stiochiometry is known as the "Mechanism of the reaction". An in a sequence of reactions leading to the formation of products from reactants, the slowest step is the rate determining step.
The mechanism proposed for the above reaction is a two step one.
The reason is that the reaction occurs by a series of elementary steps.
The sequence of elementary processes leading to the overall stiochiometry is known as the "Mechanism of the reaction". An in a sequence of reactions leading to the formation of products from reactants, the slowest step is the rate determining step.
The mechanism proposed for the above reaction is a two step one.
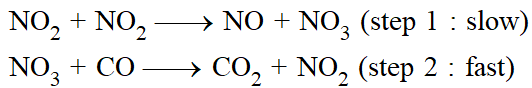 The sum of the two gives the stiochiometry & the slow step decided the rate expression.
The sum of the two gives the stiochiometry & the slow step decided the rate expression.
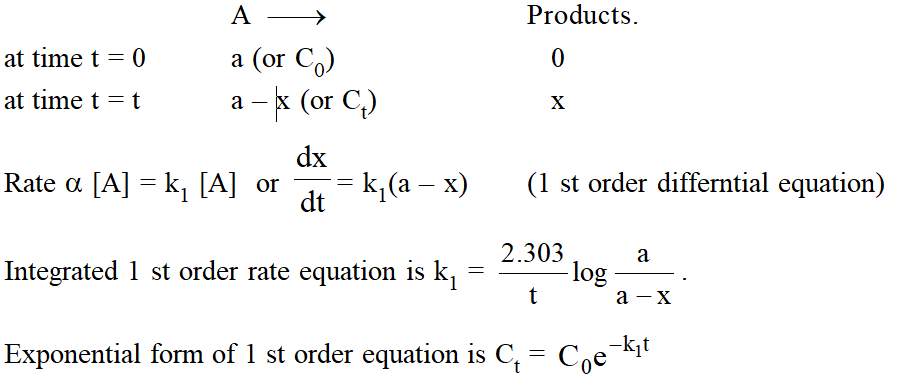 Characteristics Of First Order Reaction :
Characteristics Of First Order Reaction :
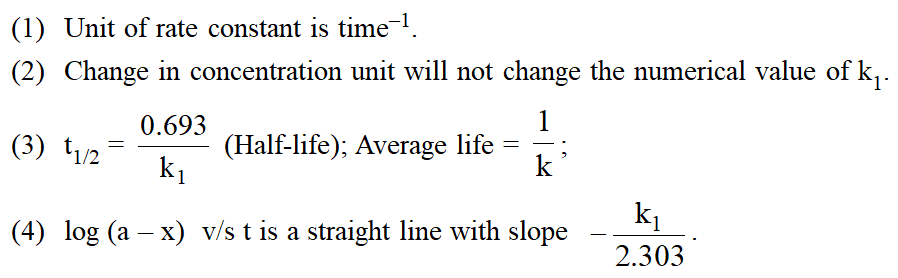 Examples :
(i) Radioactive disintegration is a first order reaction.
Examples :
(i) Radioactive disintegration is a first order reaction.
 (iii) Mineral acid catalyzed hydrolysis of esters.
(iv) Decomposition of $H_{2} O_{2}$ in aqueous solution.
Second Order Reaction :
(i) When two molecules of the same reactant are involved or the concentrations of the both reactants are equal reactions $2 \mathrm{A} \longrightarrow$ products or $\mathrm{A}+\mathrm{B} \longrightarrow$ products.
(iii) Mineral acid catalyzed hydrolysis of esters.
(iv) Decomposition of $H_{2} O_{2}$ in aqueous solution.
Second Order Reaction :
(i) When two molecules of the same reactant are involved or the concentrations of the both reactants are equal reactions $2 \mathrm{A} \longrightarrow$ products or $\mathrm{A}+\mathrm{B} \longrightarrow$ products.
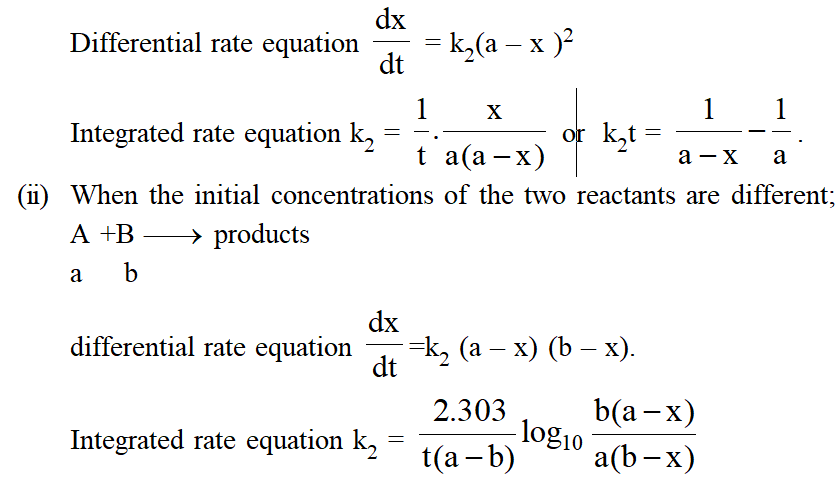 Characteristics of Second Order Reaction :
(i) Unit of rate constant L $\mathrm{mol}^{-1}$ time $^{-1}$
(ii) Numerical value of k will depend upon unit of concentration.
(iii) $\left.\mathrm{t}_{1 / 2} \propto \mathrm{a}^{-1} \text { (In general } \mathrm{t}_{1 / 2} \alpha \mathrm{a}^{(1-\mathrm{n})} ; \mathrm{n}=\text { order of reactions }\right)$
(iv) 2nd order reaction conforms to first order when one of the reactant in excess.
Examples :
Characteristics of Second Order Reaction :
(i) Unit of rate constant L $\mathrm{mol}^{-1}$ time $^{-1}$
(ii) Numerical value of k will depend upon unit of concentration.
(iii) $\left.\mathrm{t}_{1 / 2} \propto \mathrm{a}^{-1} \text { (In general } \mathrm{t}_{1 / 2} \alpha \mathrm{a}^{(1-\mathrm{n})} ; \mathrm{n}=\text { order of reactions }\right)$
(iv) 2nd order reaction conforms to first order when one of the reactant in excess.
Examples :
 Side or concurent reaction :
Side or concurent reaction :
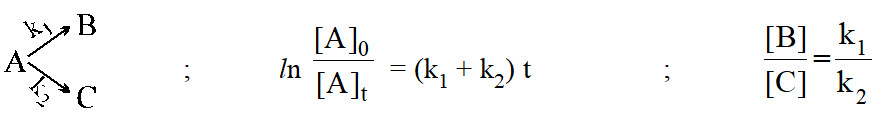 Consecutive reaction :
Consecutive reaction :
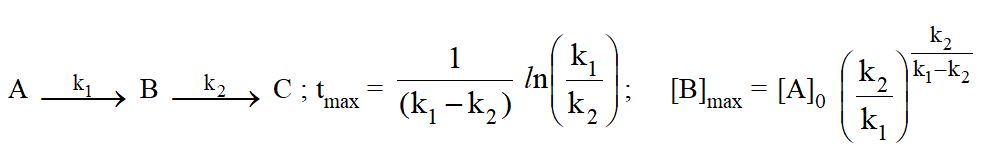 Threshold Energy and Activation Energy :
For a reaction to take place the reacting molecules must colloid together, but only those collisions, in which colliding molecules possess certain minimum energy is called threshold energy $\left(\mathrm{E}_{\mathrm{T}}\right)$.
Activation Energy $\left(\mathbf{E}_{\mathbf{a}}\right):$
The extra energy needed for the reactant molecules to be able to react chemically is known as Activation energy.
Threshold Energy and Activation Energy :
For a reaction to take place the reacting molecules must colloid together, but only those collisions, in which colliding molecules possess certain minimum energy is called threshold energy $\left(\mathrm{E}_{\mathrm{T}}\right)$.
Activation Energy $\left(\mathbf{E}_{\mathbf{a}}\right):$
The extra energy needed for the reactant molecules to be able to react chemically is known as Activation energy.
 Influence of Temperature on reaction rates :
Temperature coefficient :
The temperature coefficient of a chemical reaction is defined as the ratio of the reaction rates at two temperatures differing by $10^{\circ} \mathrm{C}$. Its value usually lies between 2 & 3.
Temperature coefficient $=\frac{\mathrm{k}_{\mathrm{t}+10}}{\mathrm{k}_{\mathrm{t}}}$
Arrhenius Equation :
Influence of Temperature on reaction rates :
Temperature coefficient :
The temperature coefficient of a chemical reaction is defined as the ratio of the reaction rates at two temperatures differing by $10^{\circ} \mathrm{C}$. Its value usually lies between 2 & 3.
Temperature coefficient $=\frac{\mathrm{k}_{\mathrm{t}+10}}{\mathrm{k}_{\mathrm{t}}}$
Arrhenius Equation :

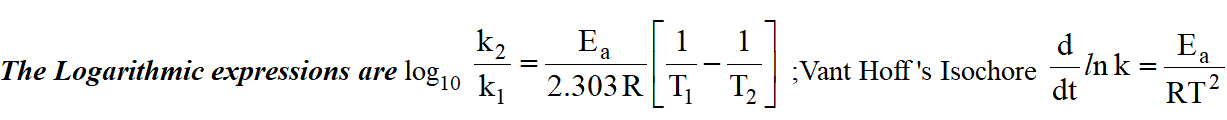 Graphical representations are :
Graphical representations are :
 Methods of Determination of order of reactions :
A few methods commonly used are given below :
1. Hit & Trial Method : It is method of using integrated rate equations, where the experimental values of a, x & t are put into these equations. One which gives a constant value of k for different sets of a, x & t correspond to the order of the reaction.
2. Graphical Method :
(i) A plot of log (a – x) versus 't' gives a straight lines for the First order reaction.
(ii) A plot of (a – x)– (n–1) versus 't' gives a straight line any reaction of the order n (except n = 1)
3.Half Life Method : The half life of different order of reactions is given by $\mathrm{a}_{\mathrm{n}}=\left(\frac{1}{2}\right)^{\mathrm{n}} \mathrm{a}_{0}$
By experimental observation of the dependence of half life on initial concentration we can determine n, the order of reaction. N $=1+\frac{\log \mathrm{t}_{2}-\log \mathrm{t}_{1}}{\log \mathrm{a}_{1}-\log \mathrm{a}_{2}}$
4. Initial rate method. Initial rate method is used to determine the order or reaction in cases where more than one reactant is used. It involves the determination of the order of different reactants separately. A series of experiments are performed in which concentration of one particular reactant is varied whereas conc. of other reactants are kept constant. In each experiment the initial rate is determined from the plot of conc. vs. time, e.g., if conc. of A is doubled, and initial rate of reaction is also doubled, order of reaction is l.
Mechanism Of reactions :
The path way which reactants are converted into the products is called the reaction mechanism. It should be clear that experimentally determined rate expression cannot be predicted from the stiochiometry of the reaction. For example for the reaction ;
Methods of Determination of order of reactions :
A few methods commonly used are given below :
1. Hit & Trial Method : It is method of using integrated rate equations, where the experimental values of a, x & t are put into these equations. One which gives a constant value of k for different sets of a, x & t correspond to the order of the reaction.
2. Graphical Method :
(i) A plot of log (a – x) versus 't' gives a straight lines for the First order reaction.
(ii) A plot of (a – x)– (n–1) versus 't' gives a straight line any reaction of the order n (except n = 1)
3.Half Life Method : The half life of different order of reactions is given by $\mathrm{a}_{\mathrm{n}}=\left(\frac{1}{2}\right)^{\mathrm{n}} \mathrm{a}_{0}$
By experimental observation of the dependence of half life on initial concentration we can determine n, the order of reaction. N $=1+\frac{\log \mathrm{t}_{2}-\log \mathrm{t}_{1}}{\log \mathrm{a}_{1}-\log \mathrm{a}_{2}}$
4. Initial rate method. Initial rate method is used to determine the order or reaction in cases where more than one reactant is used. It involves the determination of the order of different reactants separately. A series of experiments are performed in which concentration of one particular reactant is varied whereas conc. of other reactants are kept constant. In each experiment the initial rate is determined from the plot of conc. vs. time, e.g., if conc. of A is doubled, and initial rate of reaction is also doubled, order of reaction is l.
Mechanism Of reactions :
The path way which reactants are converted into the products is called the reaction mechanism. It should be clear that experimentally determined rate expression cannot be predicted from the stiochiometry of the reaction. For example for the reaction ;
Comments
Prachi
July 23, 2021, 11:53 p.m.
These short notes are really helpful for the day before the exam. Just a little issue, the presentation is quite messed up. Rest all is good! Thank you! :)
