Circles Class 9 Maths All Formulas
Class 9
Hey, students are you looking for Circles Class 9 Maths all Formulas? If yes. Then you are at the right place. In this post, I have listed all the formulas of Circles Class 9 that you can use to learn and understand the concepts easily.
If you want to improve your class 9 Math, Circles concepts, then it is super important for you to learn and understand all the formulas.
By using these formulas you will learn about the Circles concepts for class 9.
India's Best Exam Preparation for Class 9th - Download Now
With the help of these formulas, you can revise the entire chapter easily.
Circles Class 9 Maths all Formulas
Circle: It is a collection of points whose distance from a fixed point always remains constant. The fixed point is called the center of the circle and the fixed distance is called the radius of the circle. The length of the complete circle is called its circumference.
Elements of Circle
Let $P$ and $Q$ are two points on the circumference of the circle.
- Chord - Line Segment (PQ) joining any two points on a circle is called chord. Chord that passes through the center of the circle is called the diameter.1.Diameter is the longest chord. 2.All diameters have the same length, which is equal to two times the radius.
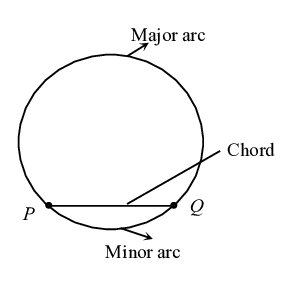
- Arc - A piece of a circle between two points is called Arc. The longer one is called the major arc and the shorter one is called the minorarc.1.When $P$ and $Q$ are ends of a diameter then both arcs are equal and each is called a semicircle.
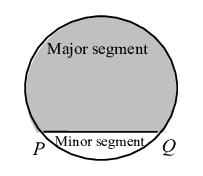
- Segment - The reginn between a chord and either of its arcs is called a segment of the circle. The larger region is called as major segment and the smaller region is called as minor segment.
- Sector - The region between an arc and the two radii, joining the center to the end points of the arc is called a sector. Larger one is called as major sector and the smaller one as minor sector.
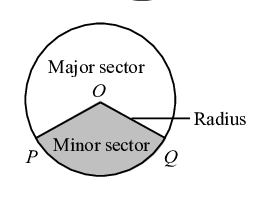1.When two arcs are equal, that is, each is a semicircle, then both segments and both sectors become the same and each is known as a semicircular region. - Tangent - A line which intersects the circle at exactly one point is called a tangent. 1.At a point of a circle there is one and only one tangent. 2.From an external point of a circle two tangents can be drawn to the circle.
- Secant - A line which intersects the circle at two distinct points is called a Secant.
India's Best Exam Preparation for Class 9th - Download Now
Properties of Circle
- Two circles are congruent if and only it they have equal radii.
- Equal chords of a circle subtend equal angles at the center. Conversely if the angles subtended by the chords at the center are equal, then chords are equal.
- The perpendicular drawn from the center of a circle to a chord bisects the chord. Conversely the line drawn from the center of a circle to bisect a chord is perpendicular to the chord.
- There is one and only one circle passing through three given non - collinear points.
- Equal chords of a circle are equidistant from the center. Conversely Chords equidistant from the center of a circle are equal in length.
- If two arcs of a circle are congruent, then their corresponding chords are equal. Conversely, if two chords of a circle are equal, then their corresponding arcs are congruent.
- Congruent arcs of a circle subtends equal angle at the center.
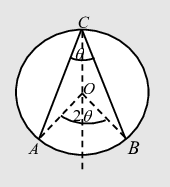
- The angle subtended by an arc at the center is double the angle subtended by it at any point on the remaining part of the circle.
- Angles in the same segment of a circle are equal.
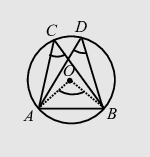
- Angle in a semicircle is a right angle.
- If a line-segment joining two points subtends equal angles at two other points lying on the same side of the line containing the line-segment, the four points lie on a circle. i.e. concyclic.
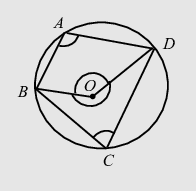
- The sum of the either pair of the opposite angles of a cyclic quadrilateral ${ }^{*}$ is $180^{\circ}$. $\angle A+\angle C=180^{\circ}$ Conversely if the sum of a pair of opposite angles of a quadrilateral is $180^{\circ}$ (i.e. supplementary), the quadrilateral is cyclic.
India's Best Exam Preparation for Class 9th - Download Now
Also Read,
Download NCERT Class 9 Maths Book in PDF
Download NCERT Class 9 Science Book in PDF
Download NCERT Class 9 Science Exemplar in PDF
Download NCERT Class 9 Maths Exemplar in PDF
If you have any Confusion related to the Introduction to Circles Class 9 Maths All Formulas, then feel free to ask in the comments section down below.
To watch Free Learning Videos on Class 9 Maths by Kota’s top Faculties Install the eSaral App