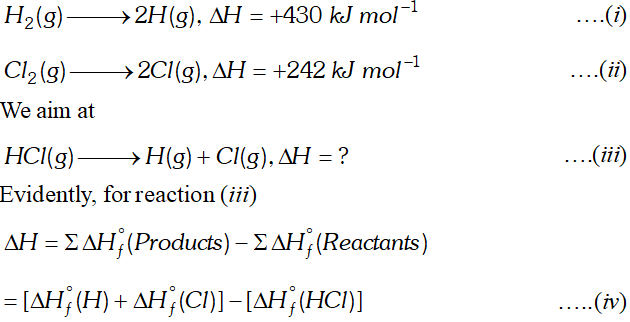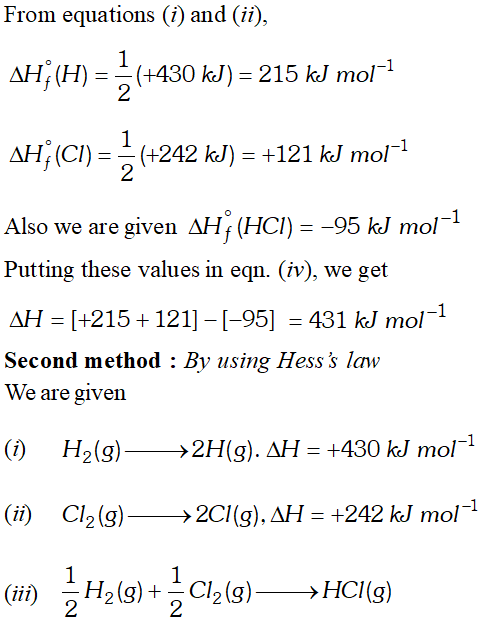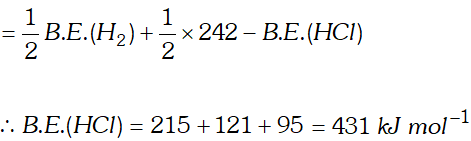Get Class 11 Chemistry Thermodynamics questions and answers to practice and learn the concepts. These important questions will play significant role in clearing concepts of Chemistry. This question bank is designed, keeping NCERT in mind and the questions are updated with respect to upcoming Board exams. You will get here all the important questions with answers for class 11 Chemistry Therodynamics and chapters. You can also Download or view Key Concepts of Thermodynamics & Thermochemistry . That will be very helpful in quick revision during Exams. Learn the concepts of class 11 Chemistry Thermodynamics topic with these important questions and answers to prepare well for the exams. Click Here for Detailed Chapter-wise Notes of Chemistry for Class 11th, JEE & NEET. You can access free study material for all three subject’s Physics, Chemistry and Mathematics. Click Here for Detailed Notes of any chapter. eSaral provides you complete edge to prepare for Board and Competitive Exams like JEE, NEET, BITSAT, etc. We have transformed classroom in such a way that a student can study anytime anywhere. With the help of AI we have made the learning Personalized, adaptive and accessible for each and every one.
Visit eSaral Website to download or view free study material for JEE & NEET. Also get to know about the strategies to Crack Exam in limited time period. Q. Is there any enthalpy change in a cyclic process ?
Ans. No, there is no enthalpy change in a cyclic process because the system returns to the initial state.
Q. What kind of system is the coffee held in a cup ?
Ans. The coffee held in a cup is an open system because it can exchange matter (water vapour) and energy (heat) with the surroundings.
Q. Why is $\Delta E=0,$ for the isothermal expansion of ideal gas?
Ans. The change in internal energy is a state function and it depends upon the temperature only. In the isothermal expansion the temperature remains constants. Therefore $\Delta E=0$ under isothermal conditions.
Q. Under what condition $\Delta H$ becomes equal to $\Delta E ?$
Ans. $\Delta H=\Delta E$ during a process which is carried out in a closed vessel $(\Delta v=0)$ or number of moles of gaseous products $=$ number of moles of gaseous reactants or the reaction does not involve any gaseous reactant or product.
Q. What is the value of internal energy for 1 mole of a mono-atomic gas ?
Ans. $E=\frac{3}{2} R T$ Mono-atomic gas.
Q. What happens to the internal energy of the system if: (i) Work is done on the system, (ii) Work is done by the system?
Ans. (i) If work is done on the system, internal energy will increase. (ii) If work is done by the system, internal energy will decrease.
Q. Will the heat released be same or different in the following two reactions : (i) $H_{2}(g)+\frac{1}{2} O_{2}(g) \rightarrow H_{2} O(l)$ (ii) $H_{2}(g)+\frac{1}{2} O_{2}(g) \rightarrow H_{2} O(g)$ Explain.
Ans. The heat released in the above two reactions will be different. It will be greater in reaction, (i) because when water (g) condense to form water (l), heat is released.
Q. How many times is molar heat capacity than specific heat capacity of water ?
Ans. 18 times.
Q. Comment on the thermodynamic stability of $N O(g),$ given (i) $\frac{1}{2} N_{2}(g)+\frac{1}{2} O_{2}(g) \rightarrow N O(g) ; \Delta_{r} H^{\circ}=90 k J \operatorname{mol}^{-1}$ (ii) $\mathrm{NO}(\mathrm{g})+\frac{1}{2} \mathrm{O}_{2}(\mathrm{g}) \rightarrow \mathrm{NO}_{2}(\mathrm{g}) ; \Delta_{r} H^{\circ}=-74 \mathrm{kJ} \mathrm{mol}^{-1}$ [NCERT]
Ans. since $\Delta_{r} H^{o}$ is +ve i.e., enthalpy of formation of $N O$ is positive, so $\mathrm{NO}(g)$ is unstable. But $\mathrm{NO}_{2}(g)$ is formed.
Q. The standard free energy of a reaction is found to be zero. What is its equilibrium constant. ?
Ans. $\Delta G^{\circ}=-2.303 R T \log K .$ Hence, $\log k=0$ or $K=1$
Q. If the polymerisation of ethylene is a spontaneous process at room temperature, predict the sign of enthalpy change during polymerization.
Ans. - For a spontaneous process, $\Delta G<0 .$ Also entropy change (\DeltaS) during polymerization is negative. According to Gibbs Helmholtz equation, $\Delta G=\Delta H-T \Delta S-v e=\Delta H-(+v e)(-v e)$ $\therefore$ The enthalpy of polymerization $\left(\Delta H_{\text {poly }}\right)$ must be negative.
Q. An exothermic reaction $X \rightarrow Y$ is spontaneous in the back direction. What is the sign of $\Delta S$ for the forward direction?
Ans. The reaction is spontaneous in the backward direction, therefore, $\Delta G$ is positive in the forward direction. Now, forward reaction is exothermic, therefore the entropy change for the forward direction should be negative and large $(T \Delta S>\Delta H)$
Q. Place the following systems in order of increasing randomness : (i) 1 mol of a gas X (ii) 1 mol of a solid X (iii) 1 mol of a liquid X. [NCERT]
Ans. Order of increasing randomness 1 Mole of solid $x<1$ mole of liquid $x<1$ mole of gas
Q. The equilibrium constant for a reactions is $10 .$ What will be the value of $\Delta G^{\circ} ?$
Ans. 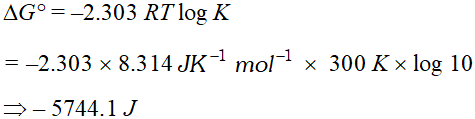
Q. What is Gibb’s Helmholtz equation ?
Ans. $\Delta G=\Delta H-T \Delta S$ where $\Delta G, H$ and $\Delta S$ are free energy change, enthalpy change and entropy change respectively.
Q. For a reaction both $\Delta H$ and $\Delta S$ are positive. Under what conditions will the reaction occur spontaneously?
Ans. - The reaction will occur spontaneously only when $T \Delta S>\Delta H$ $\Delta G=\Delta H-T \Delta S=(+)-T(+)$ For $\Delta G$ to be negative, $T \Delta S$ must be $>\Delta H$
Q. Predict the sign of entropy change in the following reactions: (i) $\quad \mathrm{O}_{2}(g)+2 S O_{2}(g) \rightarrow 2 S O_{3}(g)$ (ii) $\quad \mathrm{CaC}_{2} \mathrm{O}_{4}(\mathrm{s}) \rightarrow \mathrm{CaCO}_{3}(\mathrm{s})+\mathrm{CO}(\mathrm{g})$ (iii) $2 \mathrm{H}_{2}(\mathrm{g})+\mathrm{O}_{2}(\mathrm{g}) \rightarrow 2 \mathrm{H}_{2} \mathrm{O}(\mathrm{g})$
Ans. $-(1) \quad \Delta S=-v e$ (ii) $\quad \Delta S=+v e$ (iii) $\quad \Delta \mathrm{S}=-\mathrm{ve}$
Q. Predict the entropy change (positive/negative) in the following : (i) A liquid substance crystallises into a solid. (ii) Temperature of crytal is increased. (iii) $\quad \mathrm{CaCO}_{3}(s) \rightarrow \mathrm{CaO}(\mathrm{s})+\mathrm{CO}_{2}(\mathrm{g})$ (iv) $\quad N_{2}(g)(1 \mathrm{atm}) \rightarrow N_{2}(g)(0.5 \mathrm{atm})$ [CBSE Sample Paper for 2006] [1]
Ans. (i) $\quad \Delta S (ii) $\quad \Delta S>O$ (iii) $\quad \Delta S>O$ (iv) $\quad \Delta S>O$
Q. A reversible reaction has $\Delta G^{\circ}$ negative for forward reaction? What will be sign of for backward reaction?
Ans. Negative
Q. Which of the following are open close or nearly isolated system ? (i) Human being (ii) The earth (iii) Cane of tomato soup, (iv) Ice-cube tray filled with water, (v) A satellite in orbit, (vi) Coffee in a thermos flask, (vii) Helium filled balloon. [NCERT]
Ans. Open system : (i) Human being (ii) The earth (v) A satellite in orbit, Closed system : (iii) Cane of tomato soup, (iv) Ice cube tray filled with water, (vii) Helium filled balloon. Isolated system : (vi) Coffee in thermos flask
Q. In what way internal energy is different from enthalpy ? Explain both terms with the help of examples. [NCERT]
Ans. Internal energy : The energy of a thermodynamic system under given conditions is called internal energy. It is made up of kinetic and potential energy of constituent particles. Internal energy change is measure at constant volume. $\Delta U$ is measured in bomb calorimeter. Enthalpy is defined as heat content of the system $H=U+P V$ Enthalpy change is measured at constant pressure $\Delta H=\Delta U+P \Delta V$
Q. The enthalpy change $(\Delta H)$ for the reaction $N_{2}(g)+3 H_{2}(g) \rightarrow 2 N H_{3}(g)$ is $-92.38 k J$ at $298 K .$ What is $\Delta U$ at $298 K ? R=8.31 \mathrm{JK}^{-1} \mathrm{mol}-^{-1} . \quad$ [NCERT]
Ans. $N_{2}(g)+3 H_{2}(g) \rightarrow 2 N H_{3}(g) \Delta H=-92.38 k_{\circlearrowright}$ $\Delta n=2-4=-2$ $\Delta H=\Delta U+\Delta n R T$ $-92.38 k J=\Delta U-2 \times 8.314 \times 10^{-3} k J \times 298 k$ $\Delta U=-92.38 k J+4.955=-87.425 k J m o l^{-1}$
Q. (i) Write the relationship between $\Delta H$ and $\Delta U$ for the process at constant pressure and temperature. (ii) Calculate the value of $\Delta n$ in the following reaction: $\mathrm{CH}_{4}(\mathrm{g})+2 \mathrm{O}_{2}(\mathrm{g}) \rightarrow \mathrm{CO}_{2}(\mathrm{g})+2 \mathrm{H}_{2} \mathrm{O}(l) \cdot\left(\Delta \mathrm{U}=-85389 \mathrm{Jmol}^{-1}\right)$
Ans. (i) $\quad \Delta H=\Delta U+\Delta n R T$ (ii) $\quad \Delta n=1-3=-2$
Q. Standard vaporization enthalpy of benzene at boiling point is $30.8 \mathrm{kJ} \mathrm{mol}^{-1} ;$ for how long would a $100 \mathrm{W}$ electric heater have to operate in order to vaporize a $100 \mathrm{g}$ sample at the temperature? Power $\left.=\frac{\text { energy }}{\text { time }} \text { and } 1 W=1 \quad J s^{-1}\right)$ [NCERT]
Ans. 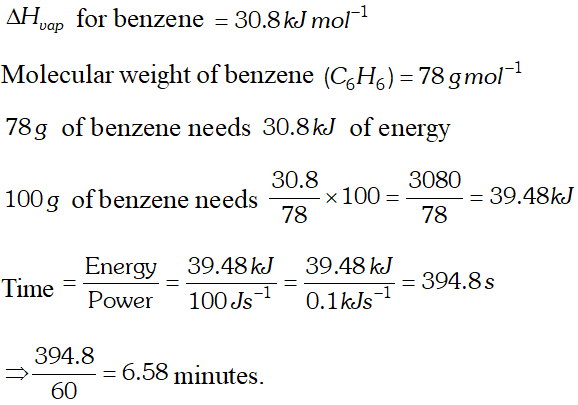
Q. Express the change in internal energy of a system when (i) No heat is absorbed by the system from the surroundings, but work (w) is done on the system. What type of wall does the system have ? (ii) No work is done on the system, but q amount of heat is taken out from the system and given to the surroundings. What type of wall does the system have? (iii) w amount of work is done by the system and q amount of heat is supplied to the system. What type of system would it be ? [NCERT]
Ans. (i) Here, $q=0$ \[ \therefore \Delta U=q+w=0+w_{a d}=w_{a d} \] As no heat is absorbed by the system, the wall is adiabatic. (ii) Here, $w=0, q=-q$ As heat is taken out, the system must be having thermally conducting walls. (iii) As work is done by the system on absorbing heat, it must be a closed system.
Q. Show that for an ideal gas, the molar heat capacity under constant volume conditions is equal to 3/2 R.
Ans. For an ideal gas, from kinetic theory of gases, the average kinetic energy per mole $\left(E_{k}\right)$ of the gas at any temperature $T K,$ is given by $E_{k}=3 / 2 R T$ At $(T+1) K,$ the kinetic energy per mole $\left(E_{k}\right)=3 / 2 R(T+1)$ Therefore, increase in the average kinetic energy of the gas for $1^{\circ} \mathrm{C}(\text { or } 1 \mathrm{K})$ rise in temperature $\Delta E_{k}=3 / 2 R(T+1)-3 / 2 R T=3 / 2 R$ When the gas is heated to raise its temperature by $1^{\circ} \mathrm{C},$ the increase in its internal energy is equal to the increase in kinetic energy, i.e., $\Delta U=\Delta E_{K}$ Now $C_{v}=\frac{\Delta U}{\Delta T}$ and $\Delta T=1^{\circ} \mathrm{C}$ $\Rightarrow C_{v}=\Delta E_{K}$ Therefore, $C_{v}=3 / 2 R$
Q. Calculate the number of $k J$ necessary to raise the temperature of $60.0 \mathrm{g}$ of aluminium from $35-55^{\circ} \mathrm{C} .$ Molarheat capacity of $A l$ is $24 J m o l^{-1} K^{-1}$
Ans. $q=c \times \Delta T, \quad c=n \times C_{m}$ Here, $C_{m}=24.0 \mathrm{J} \mathrm{mol}^{-1} \mathrm{K}^{-1} ; n=\frac{60}{27}=2.22 \mathrm{mol}$ \[ c=2.22 \mathrm{mol} \times 24.0 \mathrm{J} \mathrm{mol}^{-1} \mathrm{K}^{-1}=53.28 \mathrm{JK}^{-1} \] Now, $q=53.28 \mathrm{JK}^{-1} \times \Delta T$ $=53.28 \mathrm{JK}^{-1} \times 20 \mathrm{K}=1065.6 \mathrm{V}$ or $1.065 \mathrm{kJ}$
Q. $20.0 \mathrm{g}$ of ammonium nitrate $\left(\mathrm{NH}_{4} \mathrm{NO}_{3}\right)$ is dissolved in $125 \mathrm{g}$ of water in a coffee cup calorimeter, the temperature falls from $296.5 \mathrm{Kto} 286.4 \mathrm{K} .$ Find the value of $q$ for the calorimeter. (Hint. Treat heat capacity of water as the heat capacity of calorimeter and its content).
Ans. $q=m \times s \times\left(t_{2}-t_{1}\right)$ $q=125 g \times 4.18 J / g \times(286.4-296.5)$ $q=125 g \times 4.18 \times 10^{-3} \mathrm{kJ} / \mathrm{g} \times-10.1=-5.28 \mathrm{kJ}$
Q. Specific heat of $L i(\mathrm{s}), N a(\mathrm{s}), K(s), R b(s)$ and $C s(s)$ at $398 K$ are $3.57,1.23,0.756,0.363$ and $0.242 \mathrm{Jg}^{-1} \mathrm{K}^{-1}$ respectively. Compute the molar heat capacity of these elements and identify any periodic trend. If there is trend, use it to predict the molar heat capacity of Fr.
Ans. - Molar heat capacity $=$ specific heat capacity $\times$ molar mass So, molar heat capacity of these elements can be obtained by multiplying specific heat capacity by atomic mass. Molar heat capacity of $L i(s)=3.57 \times 7=25.01 J \mathrm{mol}^{-1} K^{-1}$ Molar heat capacity of $N a(s)=1.23 \times 23=28.3 \mathrm{J} \mathrm{mol}^{-1} \mathrm{K}^{-1}$ Molar heat capacity of $K(s)=0.756 \times 39=29.5 \mathrm{J} \mathrm{mol}^{-1} \mathrm{K}^{-1}$ Molar heat capacity of $R b(s)=0.363 \times 85=30.88 J \mathrm{mol}^{-1} \mathrm{K}^{-1}$ Molar heat capacity of $C s(s)=0.242 \times 133=32.2 \mathrm{J} \mathrm{mol}^{-1}$ The trend is that there is continuous increase of molar heat capacity with increase in atomic mass. By plotting graph between molar heat capacity and atomic mass, the molar heat capacity of $F r$ (atomic mass $=223$ ) would be $33.5 \mathrm{J} \mathrm{mol}^{-1} \mathrm{K}^{-1}$
Q. What is meant by average bond enthalpy ? In what way is it different from bond enthalpy of diatomic molecule ? Give suitable examples.
Ans. Average bond enthalpy is average heat required to break 1 mole of particular bond in various molecules (polyatomic). In diatomic molecule bond enthalpy has fixed value, $e . g . .$ in $H_{2}$ molecule $436 k J$ is bond enthalpy.
 $416 \mathrm{kJ} \mathrm{mol}^{-1}$ $H-O-H \rightarrow H(g)+O H(g) ; \Delta H=498 k_{\mathrm{d}}$ $O-H(g) \rightarrow O(g)+H(g) ; \Delta H=430 k J$ Average bond enthalpy $\Delta H(O-H)=\frac{498+430}{2}=464 k J$
$416 \mathrm{kJ} \mathrm{mol}^{-1}$ $H-O-H \rightarrow H(g)+O H(g) ; \Delta H=498 k_{\mathrm{d}}$ $O-H(g) \rightarrow O(g)+H(g) ; \Delta H=430 k J$ Average bond enthalpy $\Delta H(O-H)=\frac{498+430}{2}=464 k J$ Q. Calculate enthalpy change when $2.38 g$ of carbon monoxide (CO) vapourises at its normal boiling point. $\Delta_{v a p} H^{\ominus}$ of $C O=6.04 \mathrm{kJ} \mathrm{mol}^{-1}$
Ans. $\Delta_{v a p} H^{\ominus}$ of $C O=+6.04 \mathrm{kJmol}^{-1}$ Molar mass of $C O=28 g \mathrm{mol}^{-1}$ Energy required for vapourising $28 g$ of $C O=6.04 k_{U}$ Energy required for vapourising $2.38 g$ of $\mathrm{CO}$ $=\frac{6.04 \times 2.38}{2.8}=0.5134 k_{0} J$ or $513.4 J$
Q. Enthalpy of combustion of carbon to $\mathrm{CO}_{2}(g)$ is $-393.5 \mathrm{kJ}$ $m o l^{-1} .$ Calculate the heat released upon the formation of 35.2 $g$ of $C O_{2}$ from carbon and dioxygen gas.
Ans. $C(s)+O_{2}(g) \rightarrow C O_{2}(g) \Delta H=-393.5 k_{0} J m o l^{-1}$ Heat released for the formation of $44 g(1 \mathrm{mol})$ of $C O_{2}=-393.5 k_{U}$ Heat released for the formation of $35.2 g$ of $C O_{2}$ $\frac{-393.5 \times 35.2}{44}=-314.8 k J$
Q. The enthalpy change $(\Delta H)$ for the reaction: $N_{2}(g)+3 H_{2}(g) \rightarrow 2 N H_{3}(g)$ is $-92.38 k J$ at $298 K .$ What is $\Delta U$ at $298 K ?$
Ans. $\Delta H$ and $\Delta U$ are related as $\Delta H=\Delta U+\Delta n_{g} R T$ For the reaction $N_{2}(g)+3 H_{2}(g) \rightarrow 2 N H_{3}(g)$ $\Delta n_{g}=2-(1+3)=-2 m o l, T=298 K$ $\Delta H-92.38 k J=-92380 J, R=8.314 J K^{-1} \mathrm{mol}^{-1}$ $-92380=\Delta U-2 \times 8.314 \times 298$ $-92380=\Delta U-4955$ $\Delta U=-92380+4955=-87425 J=-87.425 k J$
Q. For the water gas reaction $\left.\mathrm{Q}_{5} \text { ) }+\mathrm{H}_{2} \mathrm{Q}(g) \rightleftharpoons \mathrm{C} Q_{g}\right)+\mathrm{H}_{2}(\mathrm{g})$ the standard Gibbs energy for the reaction at $1000 K$ is $-8.1 \mathrm{kJmol}^{-1} .$ Calculate its equilibrium constant.
Ans. We know $\Delta_{r} G^{\circ}=-2.303 R T \log K \quad$ or $\log K=\frac{-\Delta_{r} G}{2.303 R T}$ $\Delta_{r} G^{o}=-8.1 k J m o l^{-1}, T=1000 K$ $R=8.314 \times 10^{-3} \mathrm{kJ} \mathrm{mol}^{-1} \mathrm{K}^{-1}$ $\log K=-\frac{-8.1}{2.303 \times 8.314 \times 10^{-3} \times 1000}$ or $K=2.64$
Q. Red phosphorus reacts with liquid bromine as: $2 P(s)+3 B r_{2}(l) \rightarrow 2 P B r_{3}(g) \Delta_{r} H^{\circ}=-243 k J m o l^{-1}$ Calculate the enthalpy change when $10.32 g$ of phosphorus reacts with an excess of bromine.
Ans. $2 P(s)+3 B r_{2}(l) \rightarrow 2 P B r_{3}(g) \Delta_{r} H^{o}=-243 k J m o l^{-1}$ Molar mass of phosphorus $=30 \mathrm{gmol}^{-1}$ Mass of $P=10.32 \mathrm{g}$ Moles of $P=\frac{10.32}{31}=0.333 \mathrm{mol}$ Enthalpy change for 2 mole of $P=-243 \mathrm{kJ}$ Enthalpy change for 0.333 mole of $P=-\frac{243}{2} \times 0.333$ $=-40.46 \mathrm{kJ}$
Q. Standard enthalpy of vapourisation of benzene at its boiling point is $30.8 \mathrm{kJ} \mathrm{mol}^{-1} .$ For how long would a $100 \mathrm{Welectric}$ heater have to operate in order to vapourise $100 \mathrm{g}$ of benzene at its boiling point. (Given that power $=$ energy/time and $\left.1 W=1 J s^{-1}\right)$
Ans. Molar mass of benzene $\left(C_{6} H_{6}\right)=(6 \times 12)+(6 \times 1)=78$ $\therefore$ Energy required to vapourise $100 g$ benzene $=\frac{30.8}{78} \times 100=39.487 k_{U}=39487 J$ Given that power $=\frac{\text { Energy }}{\text { time }} \Rightarrow$ time $=\frac{\text { energy }}{\text { power }}$ Time $=\frac{39487 \mathrm{J}}{100 \mathrm{Js}^{-1}}=394.87 \mathrm{s}$
Q. Calculate the enthalpy change when $2.38 g$ of $C O$ vapourise at its boiling point. Given that the enthalpy of vapourisation of carbon monoxide is $6.04 \mathrm{kJ} \mathrm{mol}^{-1}$ at its boiling point of $82.0 K$
Ans. Molar mass of $C O=12+16=28$ $\Rightarrow \Delta H$ during vapourisation of $28 g=6.04 \mathrm{kJ}$ $\Delta H$ during vapourisation of $2.38 g \mathrm{CO}=\frac{6.04}{28} \times 2.38$ $=0.5134 \mathrm{kJ}$ Thus, enthalpy change $=513.4 \mathrm{J}$
Q. In the reaction $C_{3} H_{8}(g)+5 O_{2} \rightarrow 3 C O_{2}+4 H_{2} O(g) \quad$ if standard enthalpy change $\Delta H_{r}^{\circ}=-2.05 \times 10^{3} k J / m o l_{r x n}$ and bond energies of $C-C, C-H, C=O$ and $O-H$ are 347 $414,741$ and 464 respectively calculate the energy of oxygen - oxygen bond in $\mathrm{O}_{2}$ molecules.
Ans. $-\Delta H_{\text {reaction }}=-2.05 \times 10^{3} \mathrm{kJmol}$ $\Delta H=8 B_{C-H}+2 B_{C-C}+5 B_{O=O}-6 B_{C=O}-8 B_{O-H}$ $-2050 k J=8 \times 414+2 \times 347+5 B_{O=O}-6 \times 741-8 \times 464$ $-2050 k J=3312 k_{0} J+694 k J+5 B_{O=0}-4446 k J-3712 k_{\circlearrowright} J$ $-2050 k J=4006 k_{0} J+5 B_{O=0}-8158 k_{0} J$ $-2050 \mathrm{kJ}=-4152 \mathrm{kJ}+5 \mathrm{B}_{\mathrm{O}=0}$ $5 B_{O=O}=-2050+4152=+2102$ $B_{O=O}=\frac{2102}{5}=420.4 \mathrm{kJ} \mathrm{mol}^{-1}$
Q. Proceeding from $\Delta_{f} H^{\circ} \mathrm{CO}_{2}=-393.5 \mathrm{kJ} \mathrm{mol}^{-1}$ and ther mo- chemical equation: $C(\text { graphite })+2 N_{2} O(g) \rightarrow C O_{2}(g)+2 N_{2}(g)$ $\Delta_{R} H^{\circ}=-557.5 \mathrm{kJ} .$ Calculate the heat of the formation of $\mathrm{N}_{2} \mathrm{O}(\mathrm{g})$
Ans. 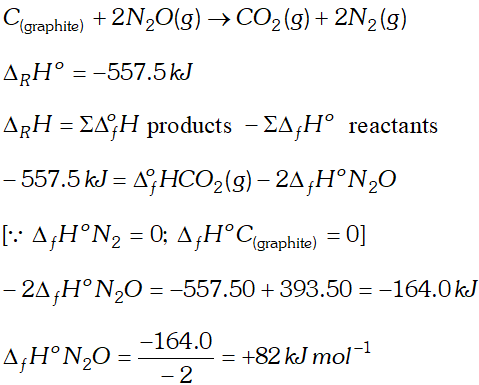
Q. Calculate $\Delta_{f} H^{\circ}$ for chloride ion from the following data: $\frac{1}{2} H_{2}(g)+\frac{1}{2} C l_{2}(g) \rightarrow H C l(g) \Delta_{f} H^{\circ}=-92.8 k J m o l^{-1}$ $H C l(g)+H_{2} O \rightarrow H_{3} O^{+}(a q)+C l^{-}(a q)$ $\Delta_{d i s s} H^{\circ}=-75.2 k J m o l^{-1}$
Ans. (i) $\quad \frac{1}{2} H_{2}(g)+\frac{1}{2} C l_{2}(g) \rightarrow H C l(g)$ \[ \Delta_{f} H^{o}=-92.8 k J m o l^{-1} \] (ii) $\quad H C l(g)+H_{2} O \rightarrow H_{3} O^{+}(a q)+C l(a q)$ \[ =\Delta_{d i s s} H^{o}=-75.2 k J m o l^{-1} \] Adding eq. ( i ) and (ii) $\frac{1}{2} H_{2}(g)+\frac{1}{2} C l_{2}(g)+H_{2} O \rightarrow H_{3} O^{+}(a q)+C l^{-}(a q)$ $\Delta H^{\circ}=-168.0 \mathrm{kJ} \mathrm{mol}^{-1}$ $\Delta H=\Delta_{f} H^{o}\left(H_{3} O^{+}\right)+\Delta_{f} H^{o}\left(C l^{-}\right)$ $-\left[\frac{1}{2} \Delta_{f} H^{o}\left(H_{2}\right)+\frac{1}{2} \Delta_{f} H^{o}\left(C l_{2}\right)\right]$ The enthalpy of formation of $H_{3} O^{+}(a q)$ in dilute solution may be taken as zero i.e., $\Delta_{f} H\left[H_{3} O^{+}(a q)\right]=0$ $-168.0=0+\Delta_{f} H^{\circ}\left(\mathrm{C} l^{-}\right)-\left[\frac{1}{2} \times 0+\frac{1}{2} \times 0\right]$ $\Delta_{f} H^{o}\left(C l^{-}\right)=-168 k J m o l^{-1}$
Q. Calculate the enthalpy change for the process : $\mathrm{CCl}_{4}(g) \rightarrow \mathrm{C}(g)+4 \mathrm{Cl}(g)$ and calculate bond enthalpy of $C$ $-C l$ bond in $C C l_{4}(g)$ $\Delta_{v a p} H^{\circ}\left(C C l_{4}\right)=30.5 k J \mathrm{mol}^{-1}$ $\Delta_{f} H^{\circ}\left(C C l_{4}\right)=-135.5 k J \mathrm{mol}^{-1}$ $\Delta_{a} H^{\circ}(C)=715.0 \mathrm{kJ} \mathrm{mol}^{-1}$ $\Delta_{a} H^{\circ}\left(C l_{2}\right)=242 k J m o l^{-1}$
Ans. The enthalpy change for the reaction: $\mathrm{CCl}_{4}(g) \rightarrow \mathrm{C}(g)+4 \mathrm{Cl}(g)$ $\Delta H^{\circ}=\Delta_{a} H^{\circ}(C)+4 \Delta_{a} H^{\circ}(C l)-\Delta_{f} H^{\circ}\left(C C l_{4}\right)(g)$ $\Delta_{a} H^{o}(C l)=715.0 \mathrm{kJ} \mathrm{mol}^{-1}$ $\Delta_{a} H^{o}(C l)=\frac{1}{2} \times 242=121 k J m o l^{-1}$ Let us first calculate $\Delta_{f} H^{\circ} \mathrm{CCl}_{4}(g)$ $C(s)+2 C l_{2}(g) \rightarrow C C l_{4}(g) \Delta H^{\circ}=-135.5 k J m o l^{-1}$ $\mathrm{CCl}_{4}(l) \rightarrow \mathrm{CCl}_{4}(\mathrm{g}) \Delta \mathrm{H}^{\circ}=30.5 \mathrm{kJ} \mathrm{mol}^{-1}$ Adding $C(s)+2 C l_{2}(g) \rightarrow C C l_{4}(g) \Delta H^{o}=-105.0 \mathrm{kJ} \mathrm{mol}^{-1}$ $\therefore \Delta H^{\circ}=715.0+4 \times 121-(-105.0)=1304.0 \mathrm{kJ} \mathrm{mol}^{-1}$ This enthalpy change corresponds to breaking four $C-C l$ bonds Bond enthalpy of $\mathrm{C}-\mathrm{Cl}$ bond $=\frac{1304.0}{4}$
Q. Predict whether it is possible or not to reduce magnesium oxide using carbon at $298 \mathrm{K}$ according to the reaction: $M g O(s)+C(s) \rightarrow M g(s)+C O(g)$ $\Delta_{r} H^{\circ}=+491.18 k J \mathrm{mol}^{-1}$ and $\Delta_{r} S^{\circ}$ $=197.67 \mathrm{JK}^{-1} \mathrm{mol}^{-1}$ If not at what temperature, the reaction becomes spontaneous.
Ans. We know $\Delta_{r} G^{\circ}=\Delta_{r} H^{o}-T \Delta_{r} S^{\circ}$ $\Delta_{r} H^{\circ}=+491.18 k J \mathrm{mol}^{-1}$ $\Delta_{r} S^{o}=197.67 \times 10^{-3} \mathrm{kJ} \mathrm{mol}^{-1} \mathrm{K}^{-1}, T=298 \mathrm{K}$ $\Delta_{r} G^{\circ}=491.18 k J \mathrm{mol}^{-1}-298 \mathrm{Kx}$ $\left(197.67 \times 10^{-3} \mathrm{kJ} \mathrm{mol}^{-1} \mathrm{K}^{-1}\right)$ $=491.18 \mathrm{kJ} \mathrm{mol}^{-1}-58.9 \mathrm{kJ} \mathrm{mol}^{-1}=432.28 \mathrm{kJ} \mathrm{mol}^{-1}$ Since Gibbs energy change is positive, therefore, at the reaction is not possible. Let us calculate $T$ at which $\Delta_{r} G^{\circ}$ becomes zero $\Delta_{r} G^{\circ}=\Delta_{r} H^{\circ}-T \Delta_{r} S^{\circ}=0$ $\therefore \quad T=\frac{\Delta_{r} H}{\Delta_{r} S}$ $=\frac{491.18 \mathrm{kJ} \mathrm{mol}^{-1}}{197.67 \times 10^{-3} \mathrm{kJ} \mathrm{mol}^{-1} \mathrm{K}^{-1}}=2484.8 \mathrm{K}$ Therefore, the reaction will be spontaneous above $2484.8 \mathrm{K}$ $\left(\text { or } 2211.8^{\circ} \mathrm{C}\right)$
Q. $20.0 \mathrm{g}$ of ammonium nitrate $\left(\mathrm{NH}_{4} \mathrm{NO}_{3}\right)$ is dissolved in $125 \mathrm{g}$ of water in a coffee-cup calorimeter. The temperature falls from $296.5 \mathrm{Kto} 286.4 \mathrm{K.Find}$ out the value of $q$ for calorimeter and its contents. Also calculate enthalpy of solution of ammonium nitrate.
Ans. Heat capacity of water $=1 \mathrm{cal} g^{-1}=4.184 \mathrm{Jg}^{-1}$ $\begin{aligned} \therefore \text { Total heat capacity of calorimeter } &=125 \times 4.184 \\ &=523 \mathrm{JK}^{-1} \end{aligned}$ $\Delta T=286.4-296.5=-10.1 K$ $\therefore$ Heat change $(q)$ for calorimeter $=$ Heat capacity $\times \Delta T$ \[ \Rightarrow q=523 \times(-10.1)=-5282.3 \mathrm{J}=-5.282 \mathrm{kJ} \] Thus, calorimeter loses $5.282 \mathrm{kJ}$ of heat during dissolution of $20 g$ of $N H_{4} N O_{3}$ in $125 g$ water Molecular mass of $N H_{4} N O_{3}$ $=(2 \times 14)+(4 \times 1)+(3 \times 16)=80$ Enthalpy of solution of $N H_{4} N O_{3}=\frac{5.282}{20} \times 80$ $=21.129 \mathrm{kJ} \mathrm{mol}^{-1}$
Q. A $1.250 \mathrm{g}$ sample of octane $\left(\mathrm{C}_{8} \mathrm{H}_{18}\right)$ is burned in excess of oxygen in a bomb calorimeter. The temperature of calorimeter rises from $294.05 K$ to $300.78 K .$ If the heat capacity of calorimeter is $8.93 \mathrm{kJK}^{-1}$, calculate the heat transferred to the calorimeter. Also calculate the enthalpy of combustion of octane.
Ans. $\Delta T=300.78-294.05=6.73 K$ Heat transferred $=$ Heat capacity $\times \Delta T$ $=\left(8.93 \mathrm{kJ} K^{-1}\right) \times(6.73 \mathrm{K})=60.0989 \mathrm{kJ}$ Molar mass of octane $\left(C_{8} H_{18}\right)=(8 \times 12)+(18 \times 1)=114$ $\therefore$ Internal energy change $(\Delta E)$ during combustion of one mole of octane $=\frac{60.0989}{1.250} \times 114=5481.02 k J \mathrm{mol}^{-1}$ Reaction of combustion of octane: $C_{8} H_{18}(l)+\frac{25}{2} O_{2}(g) \rightarrow 8 C O_{2}(g)+9 H_{2} O(l)$ $\Delta n_{g}=8-\frac{25}{2}=-\frac{9}{2}$ $\Rightarrow$ Enthalpy change, $\Delta H=\Delta E+\Delta n_{g} R T$ $\Rightarrow$ Enthalpy change, $\Delta H=\Delta E+\Delta n_{g} R T$ $=\left(5481.02 \times 10^{3}\right)+(-4.5 \times 8.314 \times 300.78)$ $=\left(5481.02 \times 10^{3}\right)-11253.08 \mathrm{J} \mathrm{mol}^{-1}$ $=5492273.082 \mathrm{Jmol}^{-1}=5492.27 \mathrm{kJ} \mathrm{mol}^{-1}$ Enthalpy of combustion of octane
Q. For the water gas reaction : $C(s)+H_{2} O(g) \rightleftarrows C O(g)+H_{2}(g)$ The standard Gibbs energy of reaction (at $1000 K)$ is $-8.1$ $k J m o l^{-1} .$ Calculate its equilibrium constant.
Ans. $\Delta G^{\circ}=-2.303 R T \log K_{p}$ or $\log K_{p}=\frac{-\Delta G^{\circ}}{2.303 \times R T}$ $=\frac{-\left(-8100 m o l^{-1}\right)}{2.303 \times 8.314 J K^{-1} m o l^{-1} \times 1000 K}=0.4230$ $\Rightarrow K_{p}=$ antilog $0.4230=2.649$
Q. Predict the sign of entropy change for each of the following changes of state: (i) $\quad H g(l) \rightarrow H g(g)$ (ii) $\quad A g N O_{3}(s) \rightarrow A g N O_{3}(a q)$ (iii) $\quad I_{2}(g) \rightarrow I_{2}(s)$ (iv) $\quad C$ (graphite) $\rightarrow C$ (diamond).
Ans. $-$ (i) $\quad S=+v e$ because liquid changes to more disordered gaseous state. (ii) $\quad \Delta S=+v e$ because aqueous solution has more disorder than solid. (iii) $\quad \Delta S=-v e$ because gas is changing to less disorder solid. (iv) because graphite has more disorder than diamond.
Q. Why would you expect a decrease in entropy as a gas condenses into liquid ? Compare it with entropy decrease when a liquid sample is converted into a solid.
Ans. As there is little order in gases are compared to liquids, therefore, entropy of gas decreases enormously on -condensation into a liquid. Also, the order of entropy for the three phases of the matter is $S(g)>>S(l)>S(s)$ Therefore, the decrease in entropy when a gas condenses into a liquid is much more as compared to decrease in entropy when a liquid solidifies.
Q. Which of the following process are accompanied by an increase of entropy: (i) Dissolution of iodine in a solvent. (ii) $\quad H C l$ is added to $A g N O_{3}$ solution and precipitate of $A g C l$ is obtained. (iii) A partition is removed to allow two gases to mix.
Ans. (i) Entropy increases due to more freedom of movement of $I_{2}$ molecules upon dissolution. (ii) Due to settling of solid $A g C l$ from solution, entropy decreases. (iii) Upon removal of partition the two gases will diffuse into one another creating greater randomness. Thus, entropy increases.
Q. The enthalpy of vaporisation of liquid diethyl ether $\left[\left(C_{2} H_{5}\right)_{2} O\right]$ is $26.0 \mathrm{kJ} \mathrm{mol}^{-1}$ at its boiling point $\left(35^{\circ} \mathrm{C}\right)$ Calculate $\Delta S$ for the conversion of: (i) Liquid to vapours and (ii) Vapours to liquid at $35^{\circ} \mathrm{C}$
Ans. $-\Delta H_{v a p}=26.0 \mathrm{kJ} \mathrm{mol}^{-1}=26000 \mathrm{J} \mathrm{mol}^{-1}$ $T_{b}=35+273=308 K$ $\Delta S_{v a p .}=\frac{\Delta H_{v a p .}}{T_{b}}=\frac{\left(26000 \mathrm{J} \mathrm{mol}^{-1}\right)}{(308 \mathrm{K})}=84.4 \mathrm{JK}^{-1} \mathrm{mol}^{-1} \mathrm{since}$ the condensation of diethyl ether is the reverse process, therefore, $\Delta S_{\text {condensation }}=-84.4 \mathrm{JK}^{-1} \mathrm{mol}^{-1}$
Q. Calculate the entropy change when $36 g$ of liquid water evaporates at $373 K\left(\Delta_{v o p} H=40.63 \mathrm{kJ} \mathrm{mol}^{-1}\right)$
Ans. $\Delta_{v a p} H=40.63 \mathrm{kJ} \mathrm{mol}^{-1}, T_{b}=373 \mathrm{K}$ $\Delta_{v a p} S=\frac{\Delta_{v a p} H}{T_{b}}=\frac{40.63 \times 1000 \mathrm{J} \mathrm{mol}^{-1}}{373 \mathrm{K}}=109 \mathrm{JK}^{-1} \mathrm{mol}^{-1}$ Entropy change for evaporation of $36 g$ of wate $\frac{109}{18} \times 36=218 \mathrm{JK}^{-1}$
Q. Silane $\left(S i H_{4}\right)$ burns in air as: $\operatorname{SiH}_{4}(g)+2 O_{2}(g) \rightarrow \operatorname{Si} O_{2}(s)+2 H_{2} O(l)$ The standard Gibbs energies of formation of $S i H_{4}(g), S i O_{2}(s)$ and $H_{2} O(l)$ are $+52.3,-805.0$ and $-228.6 \mathrm{kJmol}^{-1}$ respectively. Calculate Gibbs energy change for the reaction is spontaneous or not.
Ans. $\mathrm{SiH}_{4}(g)+2 \mathrm{O}_{2}(g) \longrightarrow \mathrm{SiO}_{2}(g)+2 \mathrm{H}_{2} \mathrm{O}(g)$ $\Delta_{r} G^{\circ}=\Delta_{f} G^{\circ}\left(S i O_{2}\right)+2 \Delta_{f} G^{\circ}\left(H_{2} O\right)-\left[\Delta_{f} G^{\circ}\left(S i H_{4}\right)\right]+$ $2 \Delta_{f} G^{\circ}\left(O_{2}\right)$ $=-805.0+2(-228.6)-[+52.3+2(0)]$ $=-805.0-457.2-52.3=-1314.5 k J$ since $\Delta_{r} G^{\circ}$ is negative, the reaction will be spontaneous.
Q. Calculate $\Delta_{r} G^{\circ}$ for conversion of oxygen to ozone: $\frac{3}{2} O_{2}(g) \rightarrow O_{3}(g)$ at $298 K$ $K_{p}$ for this conversion is $2.47 \times 10^{-29}$
Ans. We know, $\Delta_{r} G^{\circ}=-2.303 R T \log K$ $R=8.314 \mathrm{J} \mathrm{mol}^{-1} \mathrm{K}^{-1}, T=298 \mathrm{K}, \mathrm{K}=2.47 \times 10^{-29}$ $\therefore \Delta_{r} G^{\circ}=-2.303 \times\left(8.314 \mathrm{J} \mathrm{mol}^{-1} \mathrm{K}^{-1}\right) \times(298 \mathrm{K}) \times$ $\log \left(2.47 \times 10^{-29}\right)=163.2 \mathrm{kJ} \mathrm{mol}^{-1}$
Q. Consider the following reaction: $2 N O(g)+O_{2}(g) \rightarrow 2 N O_{2}(g)$ Calculate the value of standard Gibb's energy change at 298 K and predict whether the reaction is spontaneous or not. $\left[\text { If } \Delta G_{f}^{o} N O_{2}=51.3 \Delta G_{f}^{o}(N O)=86.55\right]$
Ans. $\Delta G_{r}^{o}=\left[2 \Delta G_{f}^{o}\left(N O_{2}(g)\right)\right]-\left[2 \Delta G_{f}^{O}(N O(g))+\Delta G_{f}^{O}\left(O_{2}\right)\right]$ $=[2 \times 51.3]-[2 \times 86.55+0]$ $|=(102.6)-(173.10)=-70.50 k_{0} \mathrm{J} \mathrm{mol}^{-1}$ since, the value of $\Delta G_{r}^{\circ}$ is negative, therefore, the reaction is spontaneous.
Q. Calculate the standard entropy change for the reaction $X \Longrightarrow Y$ if the value of $\Delta H^{\circ}=28.40 \mathrm{kJ}$ and equilibrium constant is $1.8 \times 10^{-7}$ at $298 \mathrm{K} ?$
Ans. $\Delta G^{\circ}=-2.303 R T \log K$ $=-2.303 \times 8.314 \times 298 \times \log \left(1.8 \times 10^{-7}\right)=38484.4$ Now, $\Delta G^{\circ}=\Delta H^{\circ}-T \Delta S^{\circ}$ $\therefore \Delta S^{\circ}=\frac{\Delta H^{\circ}-\Delta G^{\circ}}{T}=\frac{28400-38484.4}{298}$ $=-33.84 \mathrm{JK}^{-1} \mathrm{mol}^{-1}$
Q. Calculate standard molar entropy change of the formation of gaseous propane $\left(C_{3} H_{8}\right)$ at $298 K$ $3 C(\text { graphite })+4 H_{2}(g) \rightarrow C_{3} H_{8}(g)$ Given that $S_{m}^{\circ} C(\text { graphite })=5.74 J K^{-1} m o l^{-1}$ $\mathrm{S}_{\mathrm{mH}_{2}(\mathrm{g})}^{\circ} 130.68 \mathrm{JK}^{-1} \mathrm{mol}^{-1}, \mathrm{S}_{\mathrm{mC}_{3} \mathrm{H}_{8}(\mathrm{g})}^{\circ}=270.2 \mathrm{JK}^{-1}$
Ans. $\Delta S_{\text {Reaction }}=\Sigma S_{m(\text { products })}^{\circ}-\Sigma S_{m(\text { reactants })}^{\circ}$ $S_{m C_{3} H_{8}(g)}-\left[3 \times S_{m}^{\circ} C_{(g r a p h i t e)}+4 \times S_{m H_{2}(g)}^{\circ}\right]$ $=270.2-[(3 \times 5.74)-(4 \times 130.68)] J K^{-1} \mathrm{mol}^{-1}$ $=270.2-17.22-522.72=-269.72 J K^{-1} \mathrm{mol}^{-1}$
Q. The standard Gibb's energy of reactions at $1773 \mathrm{K}$ are given $\mathbf{a} \mathbf{S}$ (i) $C+O_{2} \rightarrow C O_{2} ; \Delta G^{\ominus}=-380 k J$ (ii) $4 A l+3 O_{2} \rightarrow 2 A l_{2} O_{3} ; \Delta G^{\ominus}=+22500 \mathrm{kJ}$ (iii) $2 P b+O_{2} \rightarrow 2 P b O ; \Delta G^{\Theta}=+120 \mathrm{kJ}$ Discuss the possibility of reducing $A l_{2} O_{3}$ and $P b O$ with carbon at this temperature.
Ans. (i) The process, $2 \mathrm{Al}_{2} \mathrm{O}_{3} \longrightarrow 4 \mathrm{Al}+3 \mathrm{O}_{2}$ is non-spontaneous
because $\Delta G_{r}$ is $+22500 \mathrm{kJ} .$ When this process is coupled with combustion of $C$ to $C O_{2} .$ The net free energy change is calculated as 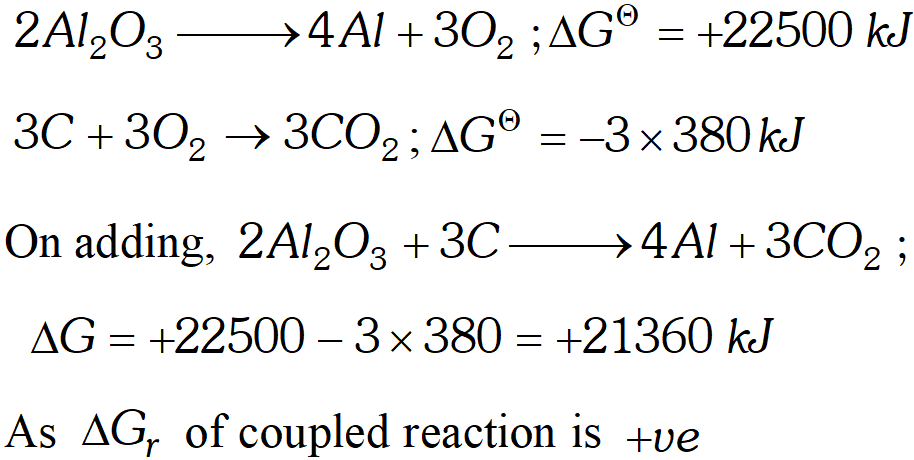 Hence it is non-spontaneous. Thus $A l_{2} O_{3}$ cannot be reduced by $C$ (ii) Let us now calculate the $\Delta G$ value for reduction of $P b O$ $2 P b O \longrightarrow 2 P b+O_{2} ; \Delta+120 k J$ $C+O_{2} \longrightarrow C O_{2} ; \Delta G=-380 k J$ On adding, $2 P b O+C \longrightarrow 2 P b+C O_{2}$ $\Delta G=120-380=-260 k J$ Hence $P b O$ can bereduced by carbon because $\Delta \mathrm{G}$ of couple reaction is $-v e$
Hence it is non-spontaneous. Thus $A l_{2} O_{3}$ cannot be reduced by $C$ (ii) Let us now calculate the $\Delta G$ value for reduction of $P b O$ $2 P b O \longrightarrow 2 P b+O_{2} ; \Delta+120 k J$ $C+O_{2} \longrightarrow C O_{2} ; \Delta G=-380 k J$ On adding, $2 P b O+C \longrightarrow 2 P b+C O_{2}$ $\Delta G=120-380=-260 k J$ Hence $P b O$ can bereduced by carbon because $\Delta \mathrm{G}$ of couple reaction is $-v e$ Q. $\Delta H$ and $\Delta S$ for the reaction: $A g_{2} O(s) \rightarrow 2 A g(s)+\frac{1}{2} O_{2}(g)$ are $30.56 \mathrm{kJ} \mathrm{mol}^{-1}$ and $66.0 \mathrm{JK}^{-1} \mathrm{mol}^{-1}$ respectively. Calculate the temperature at which the Gibbs energy change for the reaction will be zero. What will be the direction of the reaction at this temperature and below this temperature and why?
Ans. According to Gibbs Helmholtz equation, $\Delta G=\Delta H-T \Delta S$ For, $\Delta G=0$ $0=\Delta H-T \Delta S$ or $\Delta H=T \Delta S$ or $T=\frac{\Delta H}{\Delta S}$ Here, $\Delta H=30.56 \mathrm{kJ} \mathrm{mol}^{-1}=30560 \mathrm{J} \mathrm{mol}^{-1}$ $\Delta S=66.0 \mathrm{JK}^{-1} \mathrm{mol}^{-1}$ $\therefore \quad T=\frac{30560}{66.0}=463 \mathrm{K}$ (i) At $463 K,$ the reaction will be at equilibrium because $\Delta G$ is zero. (ii) Below this temperature, $\Delta G$ will be $+$ve because both $\Delta \mathrm{H}$ and $\mathrm{T} \Delta \mathrm{S}$ are positive and $\Delta \mathrm{H}>\mathrm{T} \Delta \mathrm{S}(\Delta \mathrm{H}-\mathrm{T} \Delta \mathrm{S}=+\mathrm{ve})$ Therefore, the reaction will not be spontaneous below this temperature.
Q. Calculate the standard Gibb's energy change, $\Delta G_{f}^{\circ},$ for the following reactions at $298 \mathrm{Kusing}$ standard Gibb's energy of formation. (i) $\quad C H_{4}(g)+2 O_{2}(g) \rightarrow C O_{2}(g)+2 H_{2} O(g)$ $\Delta G_{f}^{o} \mathrm{CO}_{2}(g)=-394.36 \mathrm{kJ} \mathrm{mol}^{-1}$ $\Delta G_{f}^{\circ} H_{2} O(g)=-228.57 k J m o l^{-1}$ $\Delta G_{f}^{\circ} C H_{4}(g)=-50.72 \mathrm{kJ} \mathrm{mol}^{-1}$ and $\Delta \mathrm{G}_{f}^{\circ} \mathrm{O}_{2}(g)=0$ (ii) $\operatorname{CaCQ}(s)+2 H^{+}(a q) \rightarrow C a^{2+}(a q)+H_{2} O(l)+C O_{2}(g)$ $\Delta G_{f}^{\circ} C a^{2+}(a q)=-553.58 k J m o l^{-1}$ $\Delta G_{f}^{\circ} H_{2} O(l)=-237.13 k J m o l^{-1}$ $\Delta G_{f}^{\circ} C O_{2}(g)=-394.36 k J m o l^{-1}$ $\Delta G_{f}^{o} H^{+}(a q)=0$ and $\Delta G_{f}^{o} C a C O_{3}(g)=-1206.9 \mathrm{kJ} \mathrm{mol}^{-1}$
Ans. (i) $\quad \Delta G_{f}^{\circ}=\left[\Delta G_{f}^{\circ} C O_{2}(g)+2 \times \Delta G_{f}^{\circ} H_{2} O(g)\right]$ $-\left[\Delta G_{f}^{\circ} C H_{4}(g)+2 \Delta G_{f}^{\circ} O_{2}(g)\right]$ $=[-394.36+\{2 \times(-228.57)\}-[-50.72+0]$ $=-800.78 \mathrm{kJ} \mathrm{mol}^{-1}$ (ii) $\Delta G_{r}^{\circ}=\left[\Delta G_{f}^{\circ} \mathrm{C} a^{2+}(a q)+\Delta G_{f}^{\circ} H_{2} O(l)+\Delta G_{f}^{\circ} \mathrm{CO}_{2}(g)\right]$ $\quad-\left[\Delta G_{f}^{\circ} \mathrm{CaCO}_{3}(\mathrm{s})+2 \Delta G_{f}^{\circ} \mathrm{H}^{+}(a q)\right]$ $=[-553.58+(-237.13)+(-394.36)]-[-1206.9+0]$ $=+21.83 \mathrm{kJ} \mathrm{mol}^{-1}$ (ii) $\quad \Delta G_{r}^{\circ}=\left[\Delta G_{f}^{\circ} \mathrm{C} a^{2+}(a q)+\Delta G_{f}^{\circ} H_{2} \mathrm{O}(l)+\Delta G_{f}^{\circ} \mathrm{CO}_{2}(g)\right]$ $-\left[\Delta G_{f}^{\circ} \mathrm{CaCO}_{3}(s)+2 \Delta G_{f}^{\circ} H^{+}(a q)\right]$ $=[-553.58+(-237.13)+(-394.36)]-[-1206.9+0]$ $=+21.83 \mathrm{kJ} \mathrm{mol}^{-1}$
Q. Calculate the standard molar entropy change for the following reactions at $298 K$ (i) $\quad 4 F e(s)+3 O_{2}(g) \rightarrow 2 F e_{2} O_{3}(s)$ $S^{\circ}(F e(s))=27.28 \mathrm{JK}^{-1} \mathrm{mol}^{-1}$ $S^{\circ}\left(O_{2}(g)\right)=205.14 J K^{-1} m o l^{-1}$ $S^{\circ}\left(F e_{2} O_{3}(s)\right)=87.4 \quad J K^{-1} m o l^{-1}$ (ii) $\quad C a(s)+2 H_{2} O(l) \rightarrow C a(O H)_{2}(a q)+H_{2}(g)$ $S(C a(s))^{\circ}=41.42 \quad J K^{-1} m o l^{-1}$ $S^{\circ}\left[H_{2} O(l)\right]=69.91 J K^{-1} m o l^{-1}$ $S^{\circ} \mathrm{Ca}(\mathrm{OH})_{2}(a q)=-74.50 \mathrm{JK}^{-1} \mathrm{mol}^{-1}$ $S^{\circ}\left(H_{2}\right)(g)=130.68 J K^{-1} m o l^{-1}$
Ans. (i) $\quad \Delta S_{\text {reaction}}^{\circ}=\Sigma S^{\circ}(\text { product })-\Sigma S^{\circ}(\text { reactants })$ $=\left(2 S_{F e_{2} O_{3}}^{\circ}\right)-\left(4 S_{F e(s)}^{\circ}+3 S_{O_{2}}^{\circ}(g)\right)$ $=(2 \times 87.4)-(4 \times 27.28+3 \times 205.14)$ $=(174.8)-(109.12+615.42)$ $=(174.8)-(724.54)=-549.74 \mathrm{JK}^{-1} \mathrm{mol}^{-1}$ (ii) $\quad \Delta S_{\text {reaction}}^{\circ}=\Sigma S^{\circ}(\text { products })-\Sigma S^{\circ}(\text { reactans })$ $=\left(S_{C a(O H)_{2}}^{\circ}(a q)+S_{H_{2}(g)}^{\circ}-\left(S_{C a(s))}^{\circ}+2 S_{H_{2} O(l)}^{\circ}\right)\right.$ $=\{-74.50+130.68\}-\{41.42+(2 \times 69.91)\}$ $\Rightarrow 56.18-(41.42+139.82) \Rightarrow-125.06 J K^{-1} \mathrm{mol}^{-1}$
Q. $A+B \rightarrow C+D$ $\Delta H=-10,000 J \mathrm{mol}^{-1}, \Delta S=-33.3 \mathrm{J} \mathrm{mol}^{-1} \mathrm{K}^{-1}$ (i) At what temperature the reaction will occur spontaneously from left to right? (ii) At what temperature, the reaction will reverse?
Ans. $\Delta G=\Delta H-T \Delta S$ At equilibrium $\Delta G=0$ so that $T=\frac{\Delta H}{\Delta S}=\frac{-10000 J m o l^{-1}}{-33.3 J K^{-1} m o l^{-1}}=300.3 \mathrm{K}$ (i) For spontaneity from left to right, $\Delta G$ should be $-v e$ for the given reaction. This will be so if $T<300.3 \mathrm{K}$ (ii) For reverse reaction to occur, should be tve for forward reaction. This will be so if
Q. Calculate the standard enthalpy of formation of $C H_{3} O H(l)$ from the following data: $\mathrm{CH}_{3} \mathrm{OH}(l)+\frac{3}{2} \mathrm{O}_{2}(g) \rightarrow \mathrm{CO}_{2}(g)+2 \mathrm{H}_{2} \mathrm{O}(l)$ $\Delta_{r} H^{\circ}=-726 k J m o l^{-1}$ $C(g)+O_{2}(g) \rightarrow C O_{2}(g) ; \Delta_{r} H^{\circ}=-393 k J m o l^{-1}$ $H_{2}(g)+\frac{1}{2} O_{2}(g) \rightarrow H_{2} O(l) ; \Delta_{r} H^{\circ}=-286.0 k J m o l^{-1}$
Ans. - The required equation for the formation of $C H_{3} O H(l)$ is : $C(\text { graphite })+2 H_{2}(g)+\frac{1}{2} O_{2}(g) \longrightarrow C H_{3} O H(l)$ The given equations are: (i) $\left.\quad \mathrm{CH}_{3} \mathrm{OH}(l)+\frac{3}{2} \mathrm{O}_{2}(g) \longrightarrow \mathrm{CO}_{2}(g)+2 \mathrm{H}_{2} \mathrm{O}(l)\right]$ (i) $\left.\quad \mathrm{CH}_{3} \mathrm{OH}(l)+\frac{3}{2} \mathrm{O}_{2}(g) \longrightarrow \mathrm{CO}_{2}(g)+2 \mathrm{H}_{2} \mathrm{O}(l)\right]$ $\Delta_{r} H^{\circ}=-726 k J m o l^{-1}$ (ii) $\quad C(g)+O_{2}(g) \longrightarrow C O_{2}(g) ; \Delta_{r} H^{\circ}=-393 k J m o r^{1}$ (iii) $H_{2}(g)+\frac{1}{2} O_{2}(g) \longrightarrow H_{2} O(\eta) ; \Delta_{r} H^{\circ}=-2860 \mathrm{kJ} \mathrm{mol}^{-1}$ Multiply eqn. (iii) by 2 and add to eqn. (ii) (ii) $C_{( \text {graphite) } }+O_{2}(g) \rightarrow C O_{2}(g) ; \Delta_{r} H^{\circ}=-393 \mathrm{kJ} \mathrm{mol}^{-1}$ (iii) $\times 2: 2 H_{2}(g)+O_{2}(g) \rightarrow 2 H_{2} O(l) ; \Delta_{r} H^{o}=-572 k J m o r^{1}$ (iv) $\quad C(g)+2 H_{2}(g)+2 O_{2}(g) \longrightarrow C O_{2}(g)+2 H_{2}^{\circ} O$ $\Delta_{r} H^{\circ}=-965 \mathrm{kJmol}^{-1}$ Subtract eq. ( $i \text { ) from eq. ( } i v)$ (i) $\quad \mathrm{CH}_{3} \mathrm{OH}(l)+\frac{3}{2} \mathrm{O}_{2}(g) \longrightarrow \mathrm{CO}_{2}+2 \mathrm{H}_{2} \mathrm{O}(l)$ $\Delta_{r} H^{\circ}=-726 \mathrm{kJmol}^{-1}$ $C_{(G r a p h i t e)}+2 H_{2}(g)+\frac{1}{2} O_{2}(g) \longrightarrow C H_{3} O H(l)$ $\Delta_{r} H^{\circ}=-239 k J m o l^{-1}$
Q. A piston exerting a pressure of 1 atm rests on the surface of water at $100^{\circ} \mathrm{C} .$ The pressure is reduced to smaller extent when $10 g$ of water evaporates and $22.2 \mathrm{kJ}$ of heat is absorbed. (iii) $\Delta U$ Calculate (i) $\Delta H, \quad$ (ii) $w$
Ans. (i) $\quad H_{2} O(l) \rightleftharpoons H_{2} O(g)$ since process occurs at constant $T$ and constant $P$ Thus heat change refers to $\Delta H$ $\therefore \quad \Delta H=+22.2 k_{0} J$ (ii) Calculation of $w$ Mol. of water vaporised $=\frac{10}{18}=0.56$ $\therefore W=-p_{e x} \Delta V \quad\left(\Delta V=\frac{n R T}{P_{e x t}}\right)$ $=-p_{e x} \frac{n R T}{P_{e x t}}=-n R T$ $=-0.56 \times 8.314 \times 10^{-3} \times 373.15=-1.737 k J$ (iii) Calculation of $\Delta U$ $\Delta H=\Delta U+P \Delta V$ $\Delta U=\Delta H-P \Delta V=\Delta H-n R T$ $=22.2-1.737=20.463 \mathrm{kJ}$
Q. Calculate the bond enthalpy of $H C l .$ Given that the bond enthalpies of $H_{2}$ and $C l_{2}$ are $430 \mathrm{kJ} \mathrm{mol}^{-1}$ and $242 \mathrm{kJ} \mathrm{mol}^{-1}$ respectively and $\Delta \mathrm{H}_{f}^{\circ}$ for $H C l s-95 k J m o l^{-1}$
Q. Calculate $\Delta S$ when 1 mole of steam at $100^{\circ} \mathrm{C}$ is converted into ice at $0^{\circ} \mathrm{C}$. Given : Average specific heat of liquid water $=1.0 \mathrm{cal} K^{-1} g^{-1} .$ Heat of vaporisation at boiling point $=539.7$ cal $g^{-1} .$ Heat of fusion at freezing point $=79.7 \mathrm{cal} g^{-1}$
Ans. $C_{p}=\left(1.0 \mathrm{cal} K^{-1} g^{-1}\right)\left(18.0 \mathrm{g} \mathrm{mol}^{-1}\right)=18.0 \mathrm{cal} \mathrm{K}^{-1} \mathrm{mol}^{-1}$ $\Delta H_{v}=\left(5397 \operatorname{cal} g^{-1}\right)\left(180 g m o l^{1}\right)=97146 \mathrm{calmol}^{1}$ $\Delta H_{f}=\left(79.7 \mathrm{cal} g^{-1}\right)\left(18.0 \mathrm{g} \mathrm{mol}^{-1}\right)=1435 \mathrm{cal} \mathrm{mol}^{-1}$ The process consists of the following reversible steps : (i) $\quad H_{2} \mathrm{O}_{( \text {steam) } }$ at $100^{\circ} \mathrm{C} \longrightarrow \mathrm{H}_{2} \mathrm{O}(l)$ at $100^{\circ} \mathrm{C}$ $\Delta S_{1}=-\frac{\Delta H_{v}}{T_{b}}=-\frac{9714.6 \mathrm{cal} \mathrm{mol}^{-1}}{373 \mathrm{K}}$ $-26.0445 \mathrm{cal} \mathrm{K}^{-1} \mathrm{mol}^{-1}$ (ii) $\quad H_{2} O(l)$ at $100^{\circ} C \longrightarrow H_{2} O(l)$ at $0^{\circ} C$ $\Delta S_{2} \int_{T_{1}}^{T_{2}} C_{p(\text {liquid})} \frac{d T}{T}=C_{p(\text {liquid})} \ln \frac{T_{2}}{T_{1}}$ $=2.303\left(18 \mathrm{cal} \mathrm{K}^{-1} \mathrm{mol}^{-1}\right) \log \frac{273}{373}$ $=-5.62 \mathrm{cal} K^{-1} \mathrm{mol}^{-1}$ (iii) $\quad H_{2} O(l)$ at $0^{\circ} C \rightarrow H_{2} O(s)$ at $0^{\circ} C$ $\Delta S_{3}=-\frac{\Delta H_{f}}{T_{f}}=-\frac{1435 \mathrm{cal} \mathrm{mol}^{-1}}{273 \mathrm{K}}=-5.26 \mathrm{cal} K^{-1} \mathrm{mol}^{-1}$
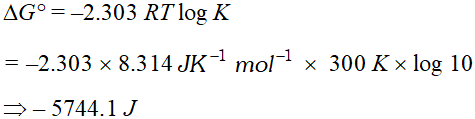
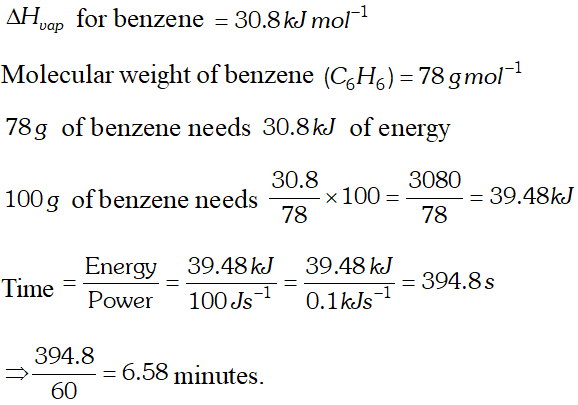
 $416 \mathrm{kJ} \mathrm{mol}^{-1}$ $H-O-H \rightarrow H(g)+O H(g) ; \Delta H=498 k_{\mathrm{d}}$ $O-H(g) \rightarrow O(g)+H(g) ; \Delta H=430 k J$ Average bond enthalpy $\Delta H(O-H)=\frac{498+430}{2}=464 k J$
$416 \mathrm{kJ} \mathrm{mol}^{-1}$ $H-O-H \rightarrow H(g)+O H(g) ; \Delta H=498 k_{\mathrm{d}}$ $O-H(g) \rightarrow O(g)+H(g) ; \Delta H=430 k J$ Average bond enthalpy $\Delta H(O-H)=\frac{498+430}{2}=464 k J$ 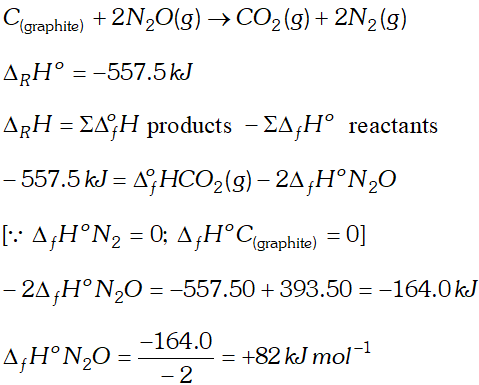
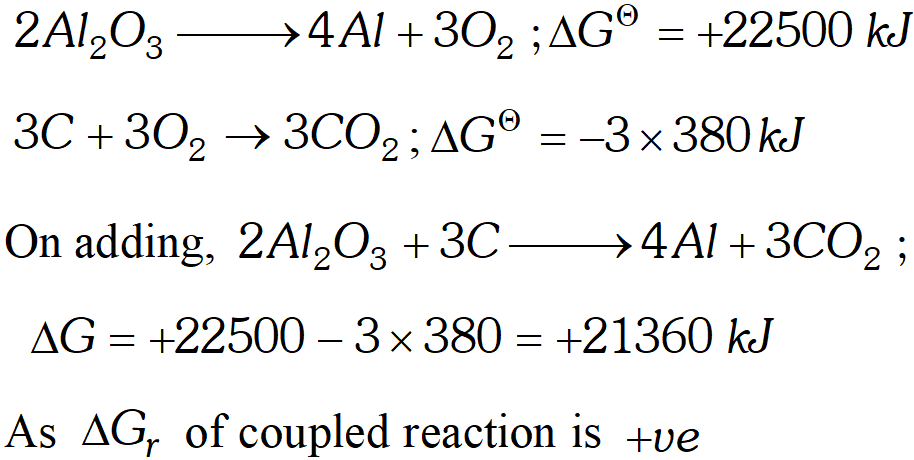 Hence it is non-spontaneous. Thus $A l_{2} O_{3}$ cannot be reduced by $C$ (ii) Let us now calculate the $\Delta G$ value for reduction of $P b O$ $2 P b O \longrightarrow 2 P b+O_{2} ; \Delta+120 k J$ $C+O_{2} \longrightarrow C O_{2} ; \Delta G=-380 k J$ On adding, $2 P b O+C \longrightarrow 2 P b+C O_{2}$ $\Delta G=120-380=-260 k J$ Hence $P b O$ can bereduced by carbon because $\Delta \mathrm{G}$ of couple reaction is $-v e$
Hence it is non-spontaneous. Thus $A l_{2} O_{3}$ cannot be reduced by $C$ (ii) Let us now calculate the $\Delta G$ value for reduction of $P b O$ $2 P b O \longrightarrow 2 P b+O_{2} ; \Delta+120 k J$ $C+O_{2} \longrightarrow C O_{2} ; \Delta G=-380 k J$ On adding, $2 P b O+C \longrightarrow 2 P b+C O_{2}$ $\Delta G=120-380=-260 k J$ Hence $P b O$ can bereduced by carbon because $\Delta \mathrm{G}$ of couple reaction is $-v e$