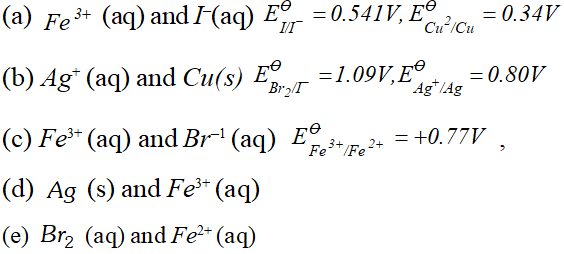Get Electrochemistry important questions with answers for Class 12 and other exams. View the Important Question bank for Class 11 & 12 Chemistry syllabus. These important questions will play significant role in clearing the concepts of Chemistry. This question bank is designed, keeping NCERT in mind and the questions are updated with respect to upcoming Board exams. You will get here all the important questions from each topic of chemistry. Learn all the concepts of Electrochemistry topic of class 12 with these important questions with answers. You can access the notes of each topic from Class 11 & 12. Click Here for Detailed Chapter-wise Notes of Chemistry for Class 11th, JEE & NEET.
You can access free study material for all three subject’s Physics, Chemistry and Mathematics. Click Here for Detailed Notes of any chapter. eSaral provides you complete edge to prepare for Board and Competitive Exams like JEE, NEET, BITSAT, etc. We have transformed classroom in such a way that a student can study anytime anywhere. With the help of AI we have made the learning Personalized, adaptive and accessible for each and every one. Visit eSaral Website to download or view free study material for JEE & NEET. Also get to know about the strategies to Crack Exam in limited time period. Q. What is the relationship between the standard EMF of the cell and the equilibrium constant of the cell reaction at 298 K ?
Ans. $E_{c a l l}^{o}=\frac{0.0591}{n} \log K_{c}$
Q. Why is it not possible to measure the voltage of an isolated reduction half reaction or the potential of a single electrode? [H.S.B. 1995, H.S.B. 2000, P.S.B. 2000]
Ans. The reduction half reaction cannot take place alone.
Q. State the factors that influence the value of cell potential of the following cell: $M g(s)\left|M g^{2+}(a q) \| A g^{+}(a q)\right| A g(s)$ [A.I.S.B. 2003]
Ans. Concentration of $M g^{2+}$ and $A g^{+}$ ions in the solution and temperature.
Q. How is an electrochemical cell represented by cell notation? [D.S.B. 1994 Supp.]
Ans. The cell notation of an electro-chemical cell is: Anode | Anode electrolyte || Cathode electrolyte | Cathode
Q. After sometime, the voltage of an electrochemical cell becomes zero. Comment on the statement [Pb. Board 2002]
Ans. The statement is correct because the reduction potentials (E') of the two electrodes become equal at that stage. What is over voltage?
Q. What is over voltage?
Ans. It is the additional voltage required to cause electrolysis.
Q. Which allotropic form of carbon is used for making electrodes? [H.P. Board 2002]
Ans. Graphite is used for making electrodes as it is a good conductor of electricity.
Q. Write Nernst equation for the following cell reaction: $Z n(s)\left|Z n^{2+}(a q) \| \quad C u^{2+}(a q)\right| C u(s)$ [Pb. Board 2006]
Ans. $E_{c e l l}=E_{c l l}^{o}-\frac{0.0591}{2} \log \frac{\left[Z n^{2+}(a q)\right]}{\left[C u^{2+}(a q)\right]}$
Q. Can a solution of $\mathrm{ZnSO}_{4}$ be stored in a vessel made up of copper?
Ans. Yes, the solution can be safely stored since copper is placed above zinc in the electrochemical series and is a weaker reducing agent. It cannot lose electrons to $Z n^{2+}(a q)$ ions.
Q. What are the units of molar conductivity? [A.I.S.B. 1994, H.S.B. 2001]
Ans. $\mathrm{Ohm}^{-1} \mathrm{cm}^{2} \mathrm{mol}^{-1}$ or $\mathrm{S} \mathrm{cm}^{2} \mathrm{mol}^{-1}$
Q. What is the relationship between specific conductance and equivalent conductance? [P.S.B. 1997, 2000]
Ans. $\Lambda_{\mathrm{eq}}=k \times V$ where $V=$ volume in $\mathrm{cm}^{3}$ containing $1 \mathrm{g} \mathrm{eq}-$ of the substance.
Q. Why is not possible to determine $\wedge_{m}^{\infty}$ for weak electrolytes by extrapolation? [Haryana Board 2001]
Ans. Because $\wedge_{m}^{\infty}$ for weak electrolytes does not increase linearly with dilution as in case of strong electrolytes.
Q. How is $\wedge_{m}^{\infty}$ of weak electrolytes calculated according to Kohlrausch’s law? [Haryana Board 2005]
Ans. $\wedge_{m}^{\infty}$ of weak electrolytes is calculated in terms of strong electrolytes. For example, $\wedge_{m}^{\infty} C H_{3} C O O H=\wedge_{m}^{\infty} C H_{3} C O O N a+\wedge_{m}^{\infty} H C l-\wedge_{m}^{\infty} N a C l$
Q. Which is evolved at cathode when an aqueous solution of NaClis electrolysed? [D.S.B. 2004 Supp.]
Ans. Hydrogen gas is evolved at cathode.
Q. What is the function of platinised platinum in the standard hydrogen electrode? [D.S.B. 1996]
Ans. It acts as inert electrode responsible for the electrical conductance in the standard hydrogen electrode.
Q. Which is the basic difference in a primary and secondary cell? [A.I.S.B. 1997]
Ans. A primary cell cannot be recharged while it is possible to recharge a secondary cell.
Q. Write an expression to relate molar conductivity of an electrolyte to its degree of dissociation. [Delhi Board 1997, A.I.S.B. 1999]
Ans. $\alpha=\frac{\wedge_{m}^{c}}{\wedge_{m}^{\infty}}$
Q. What will happen to the value of emf of the cell Zn $|$ Zn $^{2+}(0.1 M) \| C u^{2+}(0.1 M) | C u,$ if the concentration of the electrolyte in the anode compartment is increased [Delhi Board 2001]
Ans. EMF of the cell increases
Q. What would happen if the protective tin coating over on iron bucket is broken in some places [Delhi Board 2002]
Ans. If the protective tin coating over an iron bucket is broken at some place then iron corrodes faster than it does in the absence of Sn as oxidation potential of Fe is higher than that of Sn.
Q. Which solution will allow greater conductance of electricity, $1 M N a C l$ at $293 \mathrm{Kor} 1 \mathrm{MNaCl}$ at $323 \mathrm{K}$ [Delhi Board 2003]
Ans. $1 M N a C l$ at $323 K$ as the ionic mobilities increase with increase in temperature.
Q. Give one point of distinction between emf and potential difference [Haryana Board 1997]
Ans. emf is the difference in the electrode potentials when no current flows through the cell while potential difference is the difference in the electrode potentials when current flows through the cell.
Q. Define the following terms: Specific and equivalent conductance [H.S.B. Sample Paper 1991, D.S.B. 1992]
Ans. Specific conductance is the conductance of 1 cm3 of the solution whereas equivalent conductance is the conductance of a solution containing one gram equivalent of the electrolyte provided the distance between the electrodes is 1 cm and area of the electrodes is so large that the whole solution is contained between them.
Q. On passing one faraday of charge, on gram mole of the substance is deposited on the cathode. Comment [Haryana Board 2000]
Ans. The statement is wrong. One gram equivalent of the substance is deposited on passing one Faraday or 96500 C of charge.
Q. Rusting of iron is quicker in saline water than in ordinary water. Give reason [AISB 2002; CBSE PMT (Mains) 2005]
Ans. In saline water, the presence of $N a^{+}$ and $C l^{-}$ ions increases the conductance of the solution in contact with the metal surface. This accelerates the formation of $F e^{2+}$ ion and hence that of rust, $F e_{2} O_{3} . x H_{2} O$ Saline medium has extra salts such as sodium chloride dissolved in water. This means that it has a greater concentration of electrolyte than ordinary medium. The ions present will favour the formation of more electrochemical cells and will thus promote rusting or corrosion.
Q. What is standard hydrogen electrode? Give the reaction that occurs at this electrode when it acts as positive electrode in an electrochemical cell [Delhi Board 1996]
Ans. Standard Hydrogen electrode: It is a glass tube broaden at the base. It is provided with a side tube, through which $H_{2}$ gas at one atmosphere is passed. A platinum wire is fused in the tube. A platinum black strip is attached to the lower end of the platinum
wire. It is immersed in $1 M H_{3} O^{+}$ ion solution. 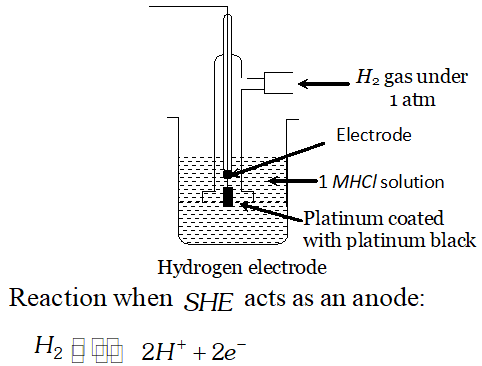
Q. What is fuel cell? Give the electrode reactions of hydrogen oxygen fuel cells [A.I.S.B. 1996,2001,2006; Delhi Board 2002]
Ans. Fuel cells : These are the galvanic cells in which the reactants are fed continuously into the cell and simultaneously the products are continuously removed. A most popular fuel cell is Hydrogen-oxygen fuel cell. The reactions taking place in hydrogen – oxygen fuel cell: At cathode : $O_{2}+4 H^{+}+4 e^{-} \longrightarrow 2 H_{2} O$ At anode : $2 H_{2} \longrightarrow 4 H^{+}+4 e^{-}$ Net reaction $: 2 \mathrm{H}_{2}+\mathrm{O}_{2} \longrightarrow 2 \mathrm{H}_{2} \mathrm{O}$
Q. With the help of a graph explain why it is not easy to determine $\lambda_{m}^{\infty}$ for a weak electrolyte by extrapolating the concentration $-$ molar conductance curve as for strong electrolytes [Delhi Board 1998]
Ans. Extrapolation of concentration molar concentration curve $\rightarrow$ The curve in case of weak electrolytes is shown below:
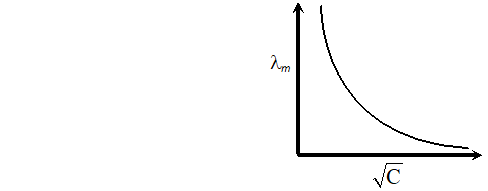 Obviously $\wedge_{m}^{\infty}$ means molar conductance at infinite dilution. This can only be obtained by extrapolating the curve. The point at $y$ -axis where it meets of extrapolation is the value of It is apparent from the graph that in case of weak electrolytes the curve does not meet $y$ -axis on extrapolation, hence the value of can not be determined to the contrary in case of strong electrolytes the curve does meet the y-axis on extrapolation.
Obviously $\wedge_{m}^{\infty}$ means molar conductance at infinite dilution. This can only be obtained by extrapolating the curve. The point at $y$ -axis where it meets of extrapolation is the value of It is apparent from the graph that in case of weak electrolytes the curve does not meet $y$ -axis on extrapolation, hence the value of can not be determined to the contrary in case of strong electrolytes the curve does meet the y-axis on extrapolation. Q. Write the cell reactions which occur in lead storage battery (i) When the battery is in use and (ii) when the battery is on charging [Delhi Board 2004]
Ans. (i) The cell reactions during the use (discharge) of lead storage battery are
At anode $: P b(s)+S O_{4}^{2-} \longrightarrow P b S O_{4}(s)+2 e^{-}$ At cathode: $P b O_{2}+4 H^{+}+S O_{4}^{2-}+2 e^{-} \longrightarrow P b S O_{4}(s)+2 H_{2} O(l)$ Net reaction $P b+P b O_{2}+4 H^{+}+2 S O_{4}^{2-} \longrightarrow 2 P b S O_{4}(s)+2 H_{2} O(l)$ (ii) During charging of the battery, the above reactions are reversed 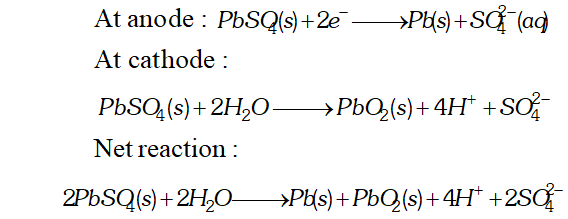
Q. Explain why electrolysis of aqueous solution of $N a C l$ gives $H_{2}$ at cathode and $C l_{2}$ anode. Write overall reaction [Delhi Board 2004,2006]
Ans. Sodium chloride and water ionize as follows $N a C l(a q .) \longrightarrow N a^{+}(a q .)+C l^{-}(a q .)$ $H_{2} O(l) \rightarrow H^{+}(a q .)+O H^{-}(a q .)$ At cathode: Both $N a^{+}$ and $H^{+}$ ions are present near the cathode. But the discharge potential of is lower than that of ions. So ions are discharged in preference to $N a^{+}$ ions $H^{+}+e^{-} \longrightarrow H ; H+H \longrightarrow H_{2}(g)$ Thus, $\mathrm{H}_{2}$ gas is liberated at the cathode and $\mathrm{Na}^{+}$ ions remain in the solution At the anode: Both $C l^{-}$ and $O H^{-}$ ions are present near the anode. As the discharge potential of $C l^{-}$ ions is lower than that of $O H^{-}$ ions, so $C l^{-}$ ions are discharged in preference to $\mathrm{OH}^{-}$ ions \[ C l^{-}-e^{-} \longrightarrow C l^{\bullet} ; \quad C l^{\bullet}+C l^{\bullet} \longrightarrow C l_{2} \] Thus $\mathrm{Cl}_{2}$ is liberated at anode and $\mathrm{OH}^{-}$ ions remain in the solution. The overall reaction is $N a C l(a q .)+H_{2} O(l) \longrightarrow N a^{+}(a q .)+O H^{-}(a q .)+1 / 2 H_{2}(g)$ $+1 / 2 C l_{2}(g)$
Q. What is corrosion? Describe the electrochemical phenomenon of rusting of Iron [Delhi Board 2005]
Ans. Corrosion is the process of slowly eating away of the metal due to attack of the atmospheric gases on the surface of the metal resulting into the formation of compounds. Such as oxides, sulphides, carbonates, etc. The corrosion of iron is called rusting. According to theory of rusting, impure iron surface behaves as a small electrochemical cell in the presence of According to theory of rusting, impure iron surface behaves as a small electrochemical cell in the presence of water containing dissolved oxygen or $\mathrm{CO}_{2} .$ The pure iron acts as anode and impure surface as cathode At anode: Iron atoms undergo oxidation spontaneously forming $F e^{2+}$ ions $F e \longrightarrow F e^{2+}(a q .)+2 e^{-} \quad E_{o x i}^{o}=-0.44 V$ $F e^{2+}$ ions move into solution and electrons into cathodic area where they are picked up by ions of the solution. At cathode: $2 H^{+}+1 / 2 O_{2}+2 e^{-} \longrightarrow H_{2} O E_{\mathrm{red}}^{\circ}=1.23 \mathrm{V}$ $\mathrm{H}^{+}$ ions are produced by secondary reactions either from $\mathrm{H}_{2} \mathrm{O}$ or from $\mathrm{H}_{2} \mathrm{CO}_{3}\left(\mathrm{CO}_{2}+\mathrm{H}_{2} \mathrm{O}\right)$ $H_{2} O \longrightarrow H^{+}+O H^{-}$ $H_{2} C O_{3} \longrightarrow H^{+}+H C O_{3}^{-}$ The overall reaction of the corrosion cell may be represent $F e(s)+2 H^{+}(a q)+1 / 2 O_{2} \longrightarrow F e^{2+}(a q)+H_{2} O ; E_{c e l l}^{o}=1.67 V$ The Fe $\mathrm{Fe}^{2+}$ ions more through water and come at the surface where these are further oxidised into $F e^{3+}$ ions by atmospheric oxygen to form hydrate ferric oxide known as rust, $F e_{2} O_{3} . . H_{2} O$ $\begin{aligned} 2 \mathrm{Fe}^{2+}+1 / 2 \mathrm{O}_{2}+2 \mathrm{H}_{2} \mathrm{O} & \longrightarrow \mathrm{Fe}_{2} \mathrm{O}_{3}+4 \mathrm{H}^{+} \\ \mathrm{Fe}_{2} \mathrm{O}_{3}+\mathrm{xH}_{2} \mathrm{O} \longrightarrow & \mathrm{Fe}_{2} \mathrm{O}_{3} \cdot \mathrm{xH}_{2} \mathrm{O} \end{aligned}$
Q. The values of $\Lambda_{m}^{\Theta}$ for $N H_{4} C l, N a O H$ and $N a C l$ at infinite are respectively $129.8,248.1$ and 126.4 ohm $^{-1} \mathrm{cm}^{2} \mathrm{mol}^{-1}$ Calculate $\wedge_{m}^{o}$ of $N H_{4} O H$ [MP Board 2005]
Ans. 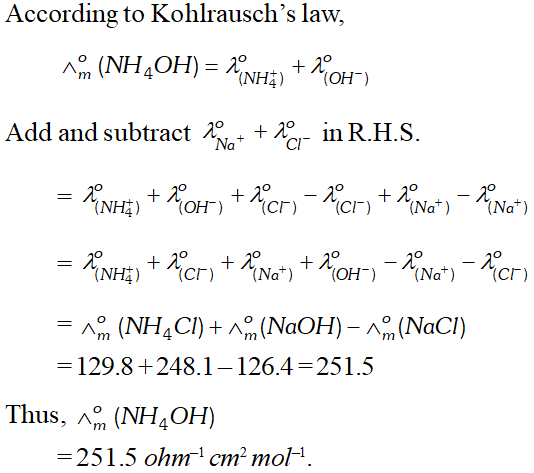
Q. Calculate the standard free energy change for the reaction occurring in the cell $Z n(s)\left|Z n^{2+}(1 M) \| C u^{2+}(1 M)\right| C u(s)$ $\left[\text { Given } E_{Z n^{2+} / Z n}^{o}=-0.76 V, E_{C u^{2+} / C u}^{o}\right.$ $\left.=0.34 V ; F=96500 \mathrm{Cmol}^{-1}\right]$ How is it related to equilibrium constant for the reaction [Delhi Board 1998]
Ans. $E_{\text {coll }}^{\circ}=E_{\text {cathode }}^{o}-E_{\text {anode }}^{o}$ $=0.34 V-(-0.76 V)=1.1 V$ Now, $\Delta G^{\circ}=-n F E_{\text {cell }}^{\circ}=-2 m o l \times 96,500 C \mathrm{mol}^{-1} \times 1.10 \mathrm{V}$ $=212300 \mathrm{J}=212.300 \mathrm{kJ}$ $\Delta \mathrm{G}^{\circ}=2.303 \mathrm{RT} \log k$
Q. Write Nernst equation and find out the emf of the following cell at $25^{\circ} \mathrm{C}$ Pt, Br $_{2} |$ Br $^{-}(0.010 \mathrm{M}) \| \mathrm{H}^{+}(0.030 \mathrm{M}) | \mathrm{H}_{2}(\text { latm }),$ Pt $\left(E_{B r / 2 B r^{-}}^{o}=+1.08 V, \quad R=8.314 J k^{-1} \mathrm{mol}^{-1}, F=96,500\left(\mathrm{mol}^{-1}\right)\right.$ [Delhi Board 1999]
Ans. Nernst equation for the reaction $M^{n+}(a q .)+n e^{-} \longrightarrow M(s)$ $E_{M^{n+} / M}=E_{M^{n+} / M}^{o}+\frac{2.303 R T}{n F} \log \left[M^{n+}\right]$ where $T$ is temperature, $n$ is valency of the ion, $F$ is faraday constant. Formula $E_{\text {cell }}=E_{r}^{\circ}-E_{l}^{\circ}+\frac{2.303 R T}{n F} \log \left[\frac{H^{+}}{B r^{-}}\right] \quad \ldots$ (i) Here, $E_{c e l l}=? E_{r}^{o}=0, E_{l}^{o}=1.08 \mathrm{V}$ $R=8.314, F=96,500 c / \mathrm{mol}, T=298 k$ and $n=1$ Substituting these values in the equation (i) we get $E_{\text {cell }}=1.08 \mathrm{V}-0+\frac{2.303 \times 8.314 \times 298}{1 \times 96,500} \log \left[\frac{0.03}{0.01}\right]$ $E_{\text {cell }}=1.08 \mathrm{V}+\frac{0.0591}{1} \log 3 \mathrm{V}$ $E_{\text {cell}}=1.08+0.0591 \times 0.4771$ $E_{\text {cell}}=1.08+0.2819 \mathrm{V}$ $=1.36$
Q. Calculate the potential (emf) of the cell $\mathrm{Cd}\left|\mathrm{Cd}^{2+}(0.10 \mathrm{M}) \| \mathrm{H}^{+}(0.20 \mathrm{M})\right| \mathrm{Pt}, \mathrm{H}_{2}(0.5 \mathrm{atm})$ (Given, $E^{o}$ for $C d^{2+} / C d=-0.403 V$ $\left.R=8.314 J k^{-1} \mathrm{mol}^{-1}, F=96,500 \mathrm{Cmol}^{-1}\right)$ [Delhi Board 1999]
Ans. 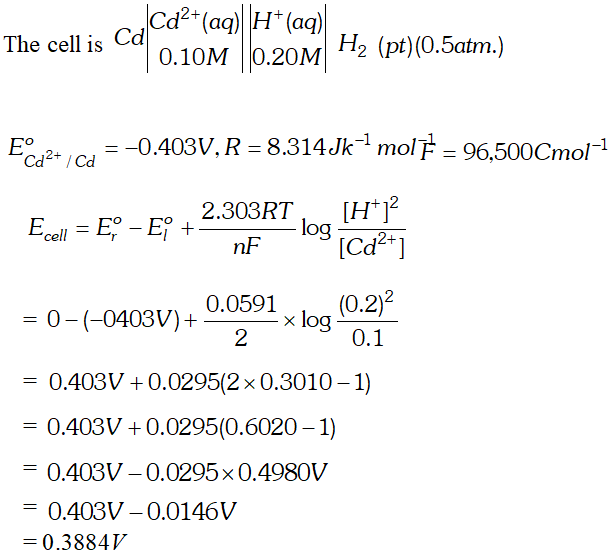
Q. Estimate the minimum potential difference needed to reduce $A l_{2} O_{3}$ at $500^{\circ} \mathrm{C} .$ The face energy change for the decomposition reaction $\frac{2}{3} A l_{2} O_{2} \longrightarrow \frac{4}{3} A l+O_{2}$ is $\Delta G=+960 \mathrm{kJ},\left(F=96,500 \mathrm{C} \mathrm{mol}^{-1}\right)$ [Delhi Board 2002]
Ans. $\mathrm{F} \mathrm{Al}_{2} \mathrm{O}_{3}+6 \mathrm{e}^{-} \longrightarrow 2 \mathrm{Al}+30^{2-} \Delta G=960 \mathrm{kJ}$ Here $n=6, \Delta G=-n F E$ $\therefore 960,000=-6 \times 96500 \times E$ $\therefore E=-1.658 V$ $\therefore$ Minimum potential difference needed to reduce $A l_{2} O_{3}$ is $1.658 V$
Q. Calculate the cell emf at $25^{\circ} \mathrm{C}$ for the following cell $M g(s)\left|M g^{2+}(0.01 M) \| S n^{2+}(0.1 M)\right| S n(s)$ (Given $E_{M g^{2+} M g}^{o}=-2.34 V . \quad E_{S n^{2}+S n}^{o}=-0.136 V$ $I F=96,500 \mathrm{Cmol}^{-1}$ Calculate the maximum work that can be accomplished by the operation of this cell [Delhi Board 2003]
Ans. $M g(s) \longrightarrow M g^{2+}(a q)+2 e^{-}$ (Anodic half reaction) $S n^{2+}(a q .)+2 e^{-} \longrightarrow S n(s)$ (Cathodic half reaction) $M g(s)+S n^{2+}(a q .) \longrightarrow M g^{2+}(a q .)+S n(s)$ $E_{c e l l}^{o}=E_{S n^{2+} / S n}^{o}-E_{M g^{2+} / M g}^{o}=-0.136+2.34$ \[ =2.204 V \] $W_{\max }=-\Delta G^{\circ}=-\left(-n F E_{c e l l}^{o}\right)=n F E_{c e l l}^{o}$ $\begin{aligned}=& 2 \times 96,500 \times 2.204 \\ &=425372 J=425.372 \mathrm{kJ} \end{aligned}$
Q. (a) Calculate the electrode potential of silver electrode dipped in a 0.1M solution of silver nitrate at $298 K$ assuming silver nitrate to be completely dissociated. The standard electrode potential of $A g^{+} / A g$ is $0.80 V$ at $298 K$ (b) At what concentration of silver ions will this electrode have a potential of zero volt [Delhi Board 2003]
Ans. 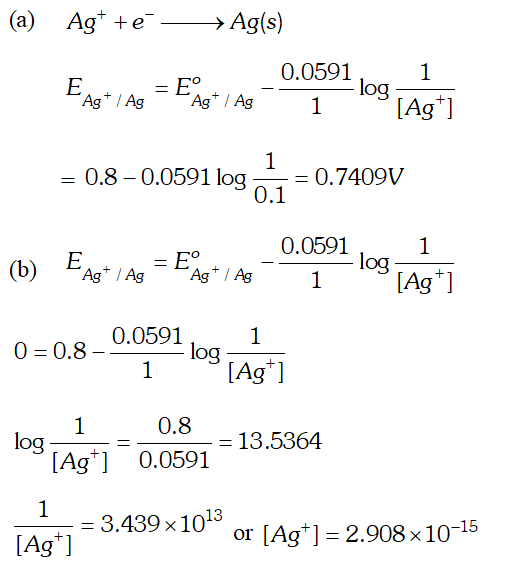
Q. Depict the galvanic cell in which the reaction $Z n(s)+2 A g^{+}(a q) \rightarrow Z n^{2+}(a q)+2 A g(s)$ takes place. Further show: (i) Which of the electrode is negatively charged (ii) The carriers of the current in the cell (iii) Individual reaction at each electrode
Ans. The electrochemical cell which will involve the given cell reaction is depicted as $Z n / Z n^{2+}(a q)|| A g^{+}(a g) / A g$ (i) In this cell, the $2 n / Z n^{2+}$ will act as negative terminal and $A g / A g^{+}$ will act as positive terminal (ii) The conventional current will flow from silver to zinc electrode in the external circuit (iii) Cathodic reaction: $2 \mathrm{Ag}^{+}+2 e^{-} \longrightarrow 2 \mathrm{Ag}$ Anodic reaction: $C u \longrightarrow C u^{2+}+2 e^{-}$
Q. Predict the products of electrolysis of the following: (i) An aqueous solution of $A g N O_{3}$ with silver electrodes (ii) An aqueous solution of $A g N O_{3}$ with platinum electrodes (iii) A dilute aqueous solution of $H_{2} S O_{4}$ with platinum electrodes (iv) An aqueous solution of cupric chloride with platinum electrodes. (Given $\left.E_{A g^{+} / A g}^{o}=+0.80 V, E_{C u^{2+} / C u}^{o}=+0.34 V\right)$
Ans. (i) Electrolysis of aqueous solution of $A g N O_{3}$ with silver electrodes. $A g N O_{3}(s)+a q \rightarrow A g^{+}(a q)+N O_{3}^{-}(a q)$ $H_{2} O \rightleftharpoons H^{+}+O H^{-}$ At cathode: $A g^{+}$ ions have lower discharge potential than $H^{+}$ ions. Hence, $A g^{+}$ ions will be deposited as Ag in preference to $H^{+}$ ions. At Anode : As $A g$ anode is attacked by $N O_{3}^{-}$ ions, $A g$ of the anode will dissolve to form $A g^{+}$ ions in the solution. $A g \longrightarrow A g^{+}+e^{-}$ (ii) Electrolysis of aqueous solution of $A g N O_{3}$ using platinum electrodes. At Cathode : Same as above. At Anode : As anode is not attackable, out of $\mathrm{OH}^{-}$ and $\mathrm{NO}_{3}^{-}$ ions, OH^- ions have lower discharge potential. Hence, $\mathrm{OH}^{-}$ ions will be discharged in preference to $\mathrm{NO}_{3}^{-}$ ions, which then decompose to given out $\mathrm{O}_{2}$ $O H^{-}(a q) \longrightarrow O H+e^{-}, 4 O H \rightarrow 2 H_{2} O(l)+O_{2}(g)$ (iii) Electrolysis of dilute $H_{2} \mathrm{SO}_{4}$ with platinum electrodes. $H_{2} S O_{4}(a q) \rightarrow 2 H^{+}(a q)+S O_{4}^{2-}(a q)$ \[ \begin{array}{l} {H_{2} O \rightleftharpoons H^{+}+O H^{-}} \\ {\text {At Cathode: } H^{+}+e \rightarrow H, \quad H+H \rightarrow H_{2}(g)} \end{array} \] At Anode: $O H^{-} \rightarrow O H+e, \quad 4 O H \rightarrow 2 H_{2} O+O_{2}(g)$ Thus, $\mathrm{H}_{2}$ is liberated at the cathode and $\mathrm{O}_{2}$ at the anode. (iv) Electrolysis of aqueous solution of $\mathrm{CuCl}_{2}$ with platinum electrodes $\mathrm{CuCl}_{2}(\mathrm{s})+a q \rightarrow \mathrm{Cu}^{2+}(a q)+2 \mathrm{Cl}^{-}(a q)$ $H_{2} O \rightleftharpoons H^{+}+O H^{-}$ At Cathode: $\mathrm{Cu}^{2+}$ ions will be reduced in preference to $\mathrm{OH}^{-}$ ions $\mathrm{Cl}^{-} \rightarrow \mathrm{Cl}+e^{-}, \mathrm{Cl}+\mathrm{Cl} \rightarrow \mathrm{Cl}_{2}(\mathrm{g})$ Thus, $C u$ will be deposited on the cathode and $C l_{2}$ will eb liberated at the anode.
Q. Predict the products of electrolysis of each of the following: (i) An aqueous solution of A g N O_{3} using silver electrodes. (ii) An aqueous solution of using platinum electrodes (iii) A dilute solution of using platinum electrodes. (iv) An aqueous solution of using platinum electrodes [C.B.S.E. Sample Paper 2003]
Ans. (i) $\quad$ An aqueous Solution of $A g N O_{3}$ using platinum electrodes: Both and water will ionise in aqueous solution
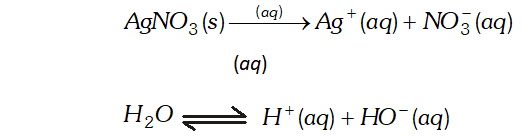 At cathode : $A g^{+}$ ions with less discharge potential are reduced in preference to $\mathrm{H}^{+}$ ions which will remain in solution. As a result, silver will be deposited at cathode. $A g^{+}(a q)+e^{-} \rightarrow A g \quad(\text { deposited })$ At anode : An equivalent amount of silver will be oxidised to Ag" ions by releasing electrons. $A g(s)-\stackrel{(a q)}{\longrightarrow} A g^{+}(a q)+e^{-}$ Thus, the concentration of the solution will remain unaffected. (ii) An aqueous solution of $A g N O_{3}$ using platinum electrodes: In the case the platinum electrodes are the non-attackable electrodes. On passing current the following changes will occur at the electrodes. At cathode : Ag" ions will be reduced to Ag which will get deposited at the cathode. At anode : Both $\mathrm{NO}_{3}^{-}$ and $\mathrm{OH}^{-}$ ions will migrate. But $\mathrm{OH}^{-}$ ions with less discharge potential will be oxidise in preference to $\mathrm{NO}_{3}^{-}$ ions which will remain in solution. $\mathrm{OH}^{-}(a q) \rightarrow \mathrm{O}+e^{-} ; 4 \mathrm{OH} \rightarrow 2 \mathrm{H}_{2} \mathrm{O}(l)+\mathrm{O}_{2}(g)$ Thus, as a result of electrolysis, silver is deposited on the cathode while $\mathrm{O}_{2}$ is evolved at the anode. The solution will be acidic due to the presence of $H N O_{3}$ (iii) A dilute solution of $H_{2} \mathrm{SO}_{4}$ using platinum electrodes: On passing current, both acid and water will ionise as follows: $H_{2} S O_{4}(l)-\stackrel{(a q)}{\longrightarrow} 2 H^{+}(a q)+S O_{4}^{2-}(a q)$
At cathode : $A g^{+}$ ions with less discharge potential are reduced in preference to $\mathrm{H}^{+}$ ions which will remain in solution. As a result, silver will be deposited at cathode. $A g^{+}(a q)+e^{-} \rightarrow A g \quad(\text { deposited })$ At anode : An equivalent amount of silver will be oxidised to Ag" ions by releasing electrons. $A g(s)-\stackrel{(a q)}{\longrightarrow} A g^{+}(a q)+e^{-}$ Thus, the concentration of the solution will remain unaffected. (ii) An aqueous solution of $A g N O_{3}$ using platinum electrodes: In the case the platinum electrodes are the non-attackable electrodes. On passing current the following changes will occur at the electrodes. At cathode : Ag" ions will be reduced to Ag which will get deposited at the cathode. At anode : Both $\mathrm{NO}_{3}^{-}$ and $\mathrm{OH}^{-}$ ions will migrate. But $\mathrm{OH}^{-}$ ions with less discharge potential will be oxidise in preference to $\mathrm{NO}_{3}^{-}$ ions which will remain in solution. $\mathrm{OH}^{-}(a q) \rightarrow \mathrm{O}+e^{-} ; 4 \mathrm{OH} \rightarrow 2 \mathrm{H}_{2} \mathrm{O}(l)+\mathrm{O}_{2}(g)$ Thus, as a result of electrolysis, silver is deposited on the cathode while $\mathrm{O}_{2}$ is evolved at the anode. The solution will be acidic due to the presence of $H N O_{3}$ (iii) A dilute solution of $H_{2} \mathrm{SO}_{4}$ using platinum electrodes: On passing current, both acid and water will ionise as follows: $H_{2} S O_{4}(l)-\stackrel{(a q)}{\longrightarrow} 2 H^{+}(a q)+S O_{4}^{2-}(a q)$ 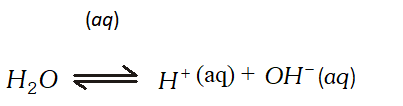 At cathode : $\mathrm{H}^{+}(\mathrm{aq})$ ions will migrate to the cathode and will be reduced to $\mathrm{H}_{2}$ H^{+}(a q)+e^{-} \longrightarrow H ; H+H \longrightarrow H_{2}(g) At anode : $O H^{-}$ ions will be released in preference to $\mathrm{SO}_{4}^{2-}$ ions because their discharge potential is less. They will be oxidised as follows: $O H^{-}(a q) \rightarrow O H+e^{-} ; 4 O H \rightarrow 2 H_{2} O(l)+O_{2}(g)$ Thus, $\mathrm{O}_{2}(g)$ will be evolved at anode. The solution will be acidic and will contain $H_{2} S O_{4} .$ (iv) An aqueous solution of $\mathrm{CuCl}_{2}$ using platinum electrodes: The electrolysis proceeds in the same manner as discussed in the case of $\mathrm{AgNO}_{3}$ solution. Both $\mathrm{CuCl}_{2}$ and $\mathrm{H}_{2} \mathrm{O}$ will ionise as follows: \begin{array}{l} {\mathrm{CuCl}_{2} \frac{(\mathrm{aq})}{2}, \mathrm{Cu}^{2+}(a q)+2 \mathrm{Cl}^{-}(a q)} \\ {\mathrm{H}_{2} \mathrm{O} \rightleftharpoons \mathrm{H}^{+}(a q)+\mathrm{OH}^{-}(a q)} \end{array} At cathode: $\mathrm{Cu}^{2+}$ ions will be reduced in preference to $\mathrm{H}^{+}$ ions and copper will be deposited at cathode $C u^{2+}(a q)+2 e^{-} \longrightarrow C u$ (deposited) At anode: $\mathrm{Cl}^{-}$ ions will be discharged in preference to $\mathrm{OH}^{-}$ ions which will remain in solution. $C l^{-} \rightarrow C l^{-}+e^{-} ; C l+C l \rightarrow C l_{2}(g)$ Thus, Cl, will be evolved at anode.
At cathode : $\mathrm{H}^{+}(\mathrm{aq})$ ions will migrate to the cathode and will be reduced to $\mathrm{H}_{2}$ H^{+}(a q)+e^{-} \longrightarrow H ; H+H \longrightarrow H_{2}(g) At anode : $O H^{-}$ ions will be released in preference to $\mathrm{SO}_{4}^{2-}$ ions because their discharge potential is less. They will be oxidised as follows: $O H^{-}(a q) \rightarrow O H+e^{-} ; 4 O H \rightarrow 2 H_{2} O(l)+O_{2}(g)$ Thus, $\mathrm{O}_{2}(g)$ will be evolved at anode. The solution will be acidic and will contain $H_{2} S O_{4} .$ (iv) An aqueous solution of $\mathrm{CuCl}_{2}$ using platinum electrodes: The electrolysis proceeds in the same manner as discussed in the case of $\mathrm{AgNO}_{3}$ solution. Both $\mathrm{CuCl}_{2}$ and $\mathrm{H}_{2} \mathrm{O}$ will ionise as follows: \begin{array}{l} {\mathrm{CuCl}_{2} \frac{(\mathrm{aq})}{2}, \mathrm{Cu}^{2+}(a q)+2 \mathrm{Cl}^{-}(a q)} \\ {\mathrm{H}_{2} \mathrm{O} \rightleftharpoons \mathrm{H}^{+}(a q)+\mathrm{OH}^{-}(a q)} \end{array} At cathode: $\mathrm{Cu}^{2+}$ ions will be reduced in preference to $\mathrm{H}^{+}$ ions and copper will be deposited at cathode $C u^{2+}(a q)+2 e^{-} \longrightarrow C u$ (deposited) At anode: $\mathrm{Cl}^{-}$ ions will be discharged in preference to $\mathrm{OH}^{-}$ ions which will remain in solution. $C l^{-} \rightarrow C l^{-}+e^{-} ; C l+C l \rightarrow C l_{2}(g)$ Thus, Cl, will be evolved at anode. Q. (a) Calculate the emf of the cell
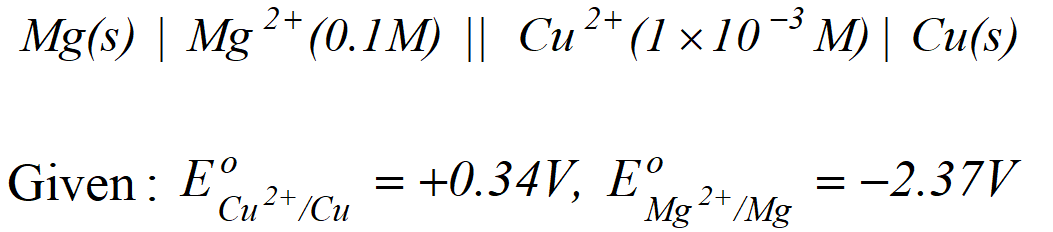 (b) Explain with example the terms weak and strong electrolytes OR (a) The resistance of a conductivity cell containing $0.001 M K C l$ solution at $298 K$ is $1500 \Omega$ what is the cell constant, it the conductivity of $0.001 \mathrm{MKCl}$ solution at $298 K$ is $0.146 \times 10^{-3} \mathrm{S} \mathrm{cm}^{-1}$ (b) Predict the product of electrolysis in the solution of H_{2} S O_{4} with platinum electrode [A.I.S.B. 2007]
(b) Explain with example the terms weak and strong electrolytes OR (a) The resistance of a conductivity cell containing $0.001 M K C l$ solution at $298 K$ is $1500 \Omega$ what is the cell constant, it the conductivity of $0.001 \mathrm{MKCl}$ solution at $298 K$ is $0.146 \times 10^{-3} \mathrm{S} \mathrm{cm}^{-1}$ (b) Predict the product of electrolysis in the solution of H_{2} S O_{4} with platinum electrode [A.I.S.B. 2007] Ans. (a) $\quad \mathrm{Cu}^{2+}+2 e^{-} \longrightarrow \mathrm{Cu} ; \mathrm{E}^{\circ}=+0.34 \mathrm{V}$
$M g-2 e^{-} \longrightarrow M g^{2+} ; E^{\circ}=+2.37 V$ $E_{\text {cell }}^{\circ}=E_{M g / M g^{2+}}^{\circ}+E_{C u^{2+} / C u}^{\circ}$ $=(2.37+0.34) V=3.71 V$ (b) Strong electrolytes are almost completely ionized when dissolved in water or any other polar solvent. In solution they are excellent conductors e.g. $N a O H$ $N a C l, K N O_{3}, H C l$ etc. Weak electrolytes are feebly ionized when dissolved in water or any other polar solvent. they are bad conductors of electricity e.g., $\mathrm{CH}_{3} \mathrm{COOH}, \mathrm{H}_{3} \mathrm{PO}_{4}, \mathrm{NH}_{4} \mathrm{OH}$ etc. OR (a) $\quad k=\frac{1}{R} \cdot \frac{l}{a}$ where $k=$ conductivity, $R=$ resistance, $l / a=\mathrm{cell}$ constant or $1 / a=R . K=1500 \times 0.146 \times 10^{-3} \mathrm{cm}$ $=0.219 \mathrm{cm}$ 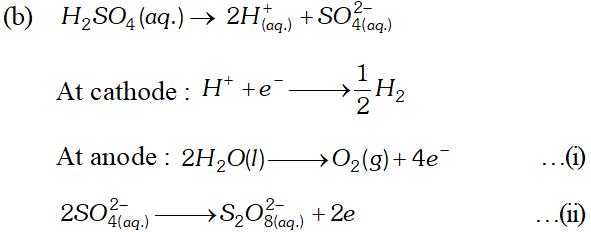 For dilute solution of $H_{2} \mathrm{SO}_{4}$ reaction (i) is preferred; in that case $\mathrm{O}_{2}$ is liberated at anode. But at higher concentration of $H_{2} S O_{4}$ reaction (ii) is preferred and peroxodisulphuric acid $\left(H_{2} S_{2} O_{8}\right)$ solution is obtained.
For dilute solution of $H_{2} \mathrm{SO}_{4}$ reaction (i) is preferred; in that case $\mathrm{O}_{2}$ is liberated at anode. But at higher concentration of $H_{2} S O_{4}$ reaction (ii) is preferred and peroxodisulphuric acid $\left(H_{2} S_{2} O_{8}\right)$ solution is obtained. Q. Calculate the emf of the cell $Z n / Z n^{2+}(0.1 M) \| C d^{2+}(0.01 M) | C d$ at $298 k$ [Given $E_{z n^{2+} / Z n}^{o}=-0.76 V$ and $E_{C d^{2}+C d}^{o}=-0.40 V$ [A.I.S.B. 2006]
Ans.
Q. When a certain conductivity cell was filled with $0.1 \mathrm{MKCl}$, it has a resistance of $85 \mathrm{W}$ at $25^{\circ} \mathrm{C}$. When the same cell was filled with an aqueous solution of $0.052 M$ unknown electrolyte, the resistance was $96 \mathrm{W}$. Calculate the molar conductivity of the unknown electrolyte at this concentration. (Specific conductivity of $0.1 M K C l=1.29 \times 10^{-2}$ ohm $^{-1} \mathrm{cm}^{-1}$ ) [Delhi Board 2004]
Ans. Resistance of $K C l$ solution, $R=85 \Omega$ Specific conductance, $k=1.29 \times 10^{-2} \Omega^{-1} \mathrm{cm}^{-1}$ Cell constant $=k \times R=1.29 \times 10^{-2} \Omega^{-1} \mathrm{cm}^{-1} \times 85 \Omega=1.1 \mathrm{cm}^{-1}$ Resistance of unknown electrolytic solution, $R=96 \Omega$ Specific conductance, $k=\frac{\text { Cell constant }}{R}=\frac{1.1 \mathrm{Cm}^{-1}}{96 \Omega}$ \[ =\frac{11}{960} \Omega^{-1} \mathrm{cm}^{-1} \] \begin{aligned} &\text { Concentration, } C=0.052 \frac{\mathrm{mol}}{L}=0.052 \frac{\mathrm{mol}}{1000 \mathrm{Cm}^{3}}\\ &=5.2 \times 10^{-5} \mathrm{mol} \mathrm{cm}^{-3}\\ &\text { Molar coductance, } \wedge_{m}=\frac{11 \Omega^{-1} C m^{-1}}{960 \times 5.2 \times 10^{-5} \mathrm{molcm}^{-3}}\\ &=220.2 \mathrm{\Omega}^{-1} \mathrm{Cm}^{2} \mathrm{mol}^{-1} \end{aligned}
Q. Calculate the potential of the following cell reaction at 298K. $S n^{4+}(1.50 M)+Z n(S) \longrightarrow S n^{2+}(0.50 M)+Z n^{2+}(2.0 M)$ The standard potential $E^{o}$ of the cell is $0.89 V$ whether the potential of the cell will increase or decrease, if the concentration of $S n^{4+}$ is increased in the cell? $\left(R=8.314 J K^{-1} \mathrm{mol}^{-1} ; F=96,500 \mathrm{Cmol}^{-1}\right)$ [Delhi Board 1997]
Ans. The cell reaction is
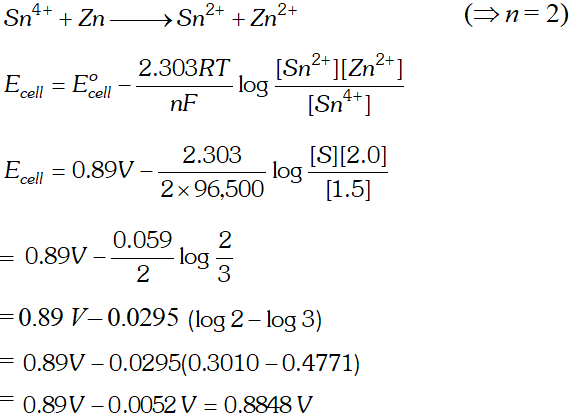
Q. Calculate the cell emf and $G$ for the cell reaction at $25^{\circ} \mathrm{C}$ for the cell
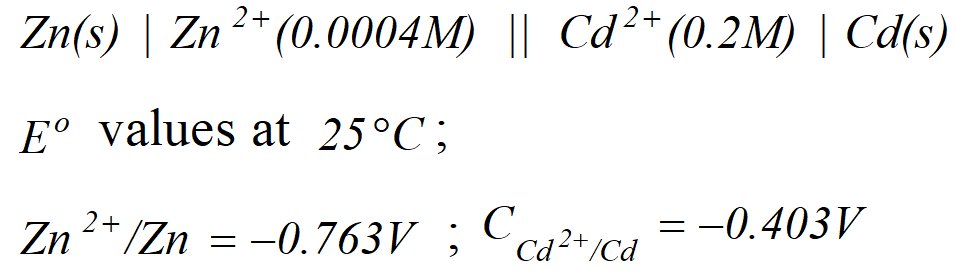
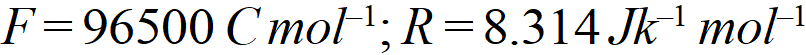 [Delhi Board 2000]
[Delhi Board 2000] Ans. $E_{\text {cell}}^{o}=E_{\text {cathode }}^{o}-E_{\text {anode }}^{\circ}=-0.403-(-0.763)=0.36 \mathrm{V}$ The net cell reaction is $Z n(s)+C d^{2+}(a q .) \rightarrow Z n^{2+}(a q .)+C d(s)$ Here value of $n=2$ $\therefore \Delta G^{\circ}=-n F E_{c e l l}^{o}=-2 \times 96,500 \times 0.36=69480 J$
Q. Using the standard electrode potentials given below, predict if the reaction between the following is feasible:
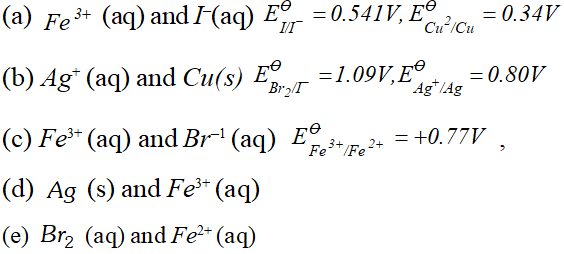
Ans. \text { (a) } \quad F e^{3+}(a q)+I^{-}(a q) \longrightarrow F e^{2+}(a q)+\frac{1}{2} I_{2}
In this reaction $F e^{3+}$ ions are reduced by $I^{-}$ ions. For this reaction to be feasibly the $E_{F e^{3+} / F e^{2+}}^{\Theta}$ should be larger than $E_{I_{2} / I^{-}}^{\Theta} .$ since the given values agree with this requirement. Hence this reaction is Feasible. \text { (b) } \quad 2 A g=(a q)+C u(s) \longrightarrow C u^{2}+2 A g In this reaction, $A g^{+}$ ions are being reduced. This is also feasible because $E_{F e^{3+} / F e^{2+}}^{\Theta}$ is less than $E_{B_{12} / B r}^{\Theta} .$ Hence Br ions cannot reduce Fe't ions. 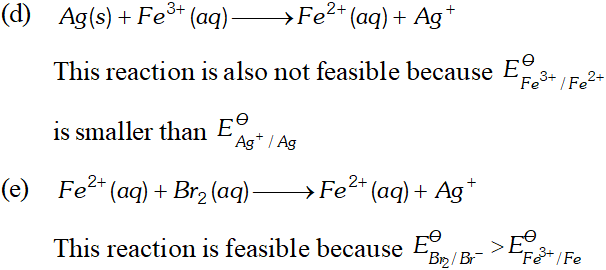
Q. Predict the products of electrolysis in each of the following: (i) An aqueous solution of $A g N O_{3}$ with silver electrodes (ii) An aqueous solution of $A g N O_{3}$ with platinum electrodes (iii) A dilute solution of $H_{2} S O_{4}$ with platinum electrodes (iv) An aqueous solution of $\mathrm{CuCl}_{2}$ with platinum electrodes.. \begin{aligned} Given that $E_{r e d}^{\Theta} H_{2} O=-0.41 V ; \quad E_{o x i}^{\theta}$ of $H_{2} O=-1.23 V ; E_{A g^{+} / A g}^{\theta}=+0.80 V ; \quad E_{C u^{2+} / C u}^{\theta}=0.34 V$
Ans. (i) $A g N O_{3} \longrightarrow A g^{+}+N O_{3}^{-}$ At cathode : $A g^{+}$ ion will reduce in preference to $H_{2} O$ $A g^{+}+e^{-} \longrightarrow A g$ At anode: $A g$ will get oxidise in preference to $\mathrm{H}_{2} \mathrm{O}$ $A g \longrightarrow A g^{+}+e^{-}$ (ii) $\quad A g N O_{3} \longrightarrow A g^{+}+N O_{3}^{-}$ At cathode: $\quad A g^{+}+e^{-} \longrightarrow A g$ At anode: $\mathrm{H}_{2} \mathrm{O}$ will oxidise in preference to $\mathrm{NO}_{3}^{-}$ ions $H_{2} O \longrightarrow 2 H^{+}+\frac{1}{2} O_{2}+2 e^{-}$ \begin{aligned} &\text { (iii) } \quad H_{2} S O_{4} \longrightarrow 2 H^{+}+S O_{4}^{2-}\\ &\text { At cathode : } 2 H^{+}+2 e^{-} \longrightarrow H_{2}\\ &\text { At anode : } H_{2} O \longrightarrow 2 H^{+}+\frac{1}{2} O_{2}+2 e^{-} \end{aligned} (iv) $\quad \mathrm{CuCl}_{2} \longrightarrow \mathrm{Cu}^{2+}+2 \mathrm{Cl}^{-}$ At cathode : $\mathrm{Cu}^{2+}$ will get reduced in preference to $\mathrm{H}_{2} \mathrm{O}$ $\mathrm{Cu}^{2+}+2 e^{-} \longrightarrow \mathrm{Cu}$ At anode: $\mathrm{Cl}^{-}$ ion will oxidise in preference to $\mathrm{H}_{2} \mathrm{O}$ $2 \mathrm{Cl} \longrightarrow \mathrm{Cl}_{2}+2 \mathrm{e}^{-}$

 Obviously $\wedge_{m}^{\infty}$ means molar conductance at infinite dilution. This can only be obtained by extrapolating the curve. The point at $y$ -axis where it meets of extrapolation is the value of It is apparent from the graph that in case of weak electrolytes the curve does not meet $y$ -axis on extrapolation, hence the value of can not be determined to the contrary in case of strong electrolytes the curve does meet the y-axis on extrapolation.
Obviously $\wedge_{m}^{\infty}$ means molar conductance at infinite dilution. This can only be obtained by extrapolating the curve. The point at $y$ -axis where it meets of extrapolation is the value of It is apparent from the graph that in case of weak electrolytes the curve does not meet $y$ -axis on extrapolation, hence the value of can not be determined to the contrary in case of strong electrolytes the curve does meet the y-axis on extrapolation. 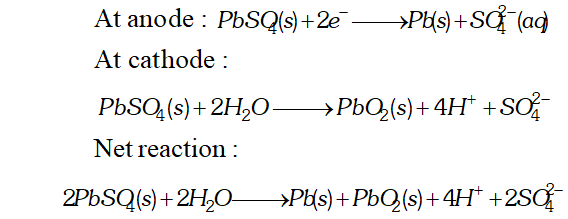
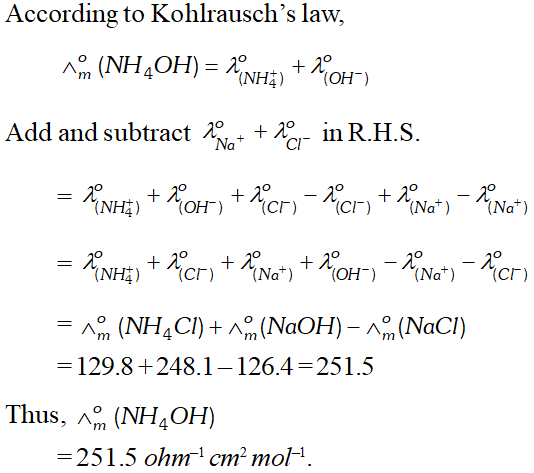
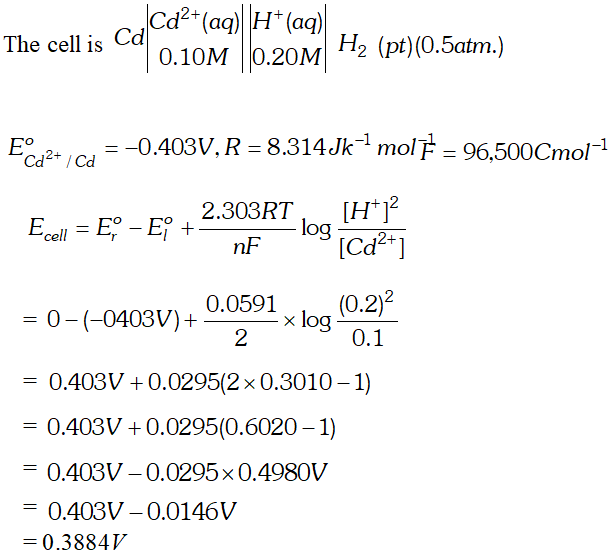
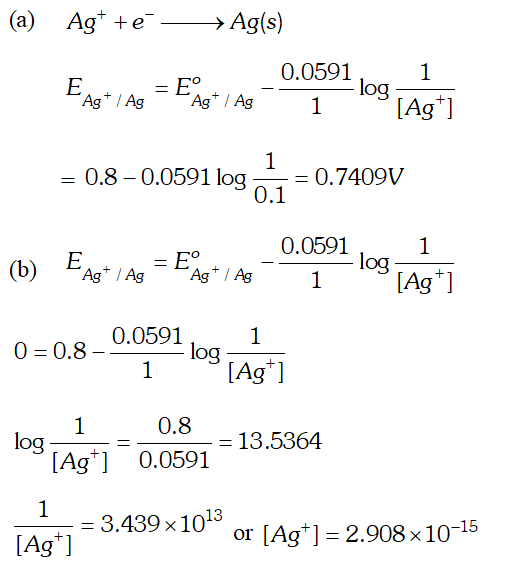
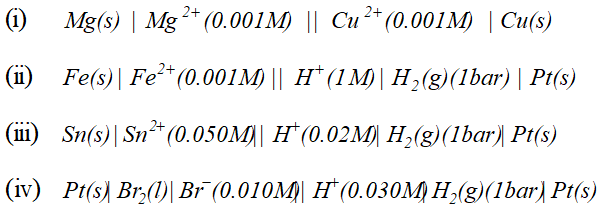
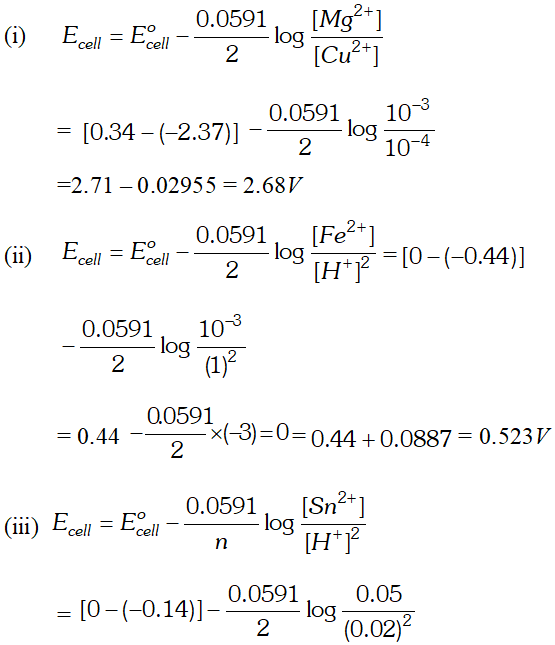
![]()
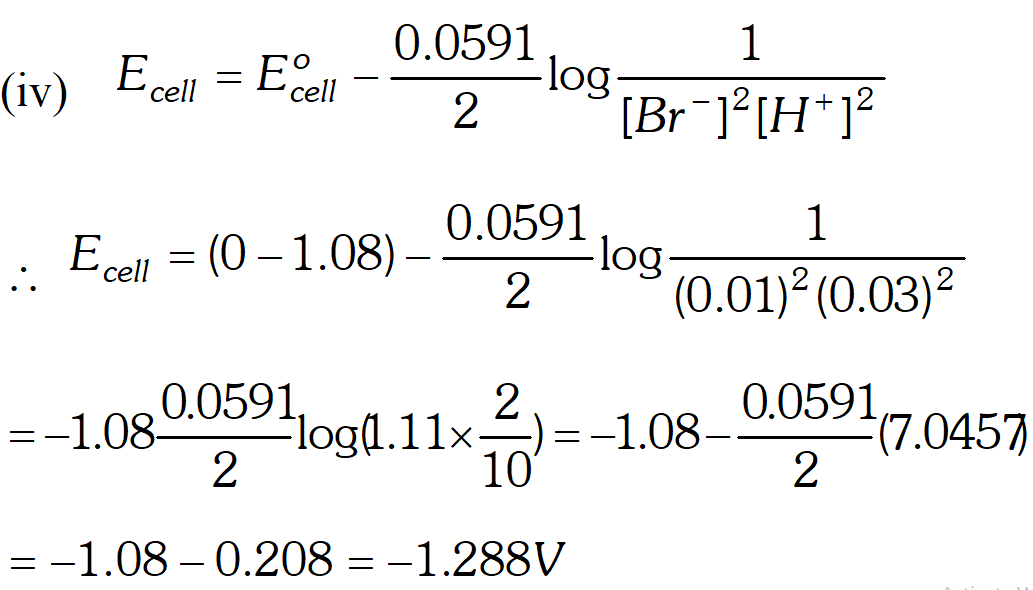 Thus oxidation will occur at hydrogen electrode and reduction on the $B r_{2}$ electrode. $E_{c e l l}=1.288 \mathrm{V}$
Thus oxidation will occur at hydrogen electrode and reduction on the $B r_{2}$ electrode. $E_{c e l l}=1.288 \mathrm{V}$ 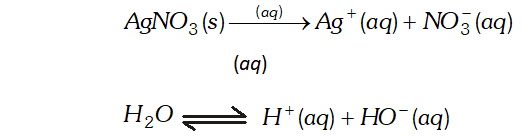 At cathode : $A g^{+}$ ions with less discharge potential are reduced in preference to $\mathrm{H}^{+}$ ions which will remain in solution. As a result, silver will be deposited at cathode. $A g^{+}(a q)+e^{-} \rightarrow A g \quad(\text { deposited })$ At anode : An equivalent amount of silver will be oxidised to Ag" ions by releasing electrons. $A g(s)-\stackrel{(a q)}{\longrightarrow} A g^{+}(a q)+e^{-}$ Thus, the concentration of the solution will remain unaffected. (ii) An aqueous solution of $A g N O_{3}$ using platinum electrodes: In the case the platinum electrodes are the non-attackable electrodes. On passing current the following changes will occur at the electrodes. At cathode : Ag" ions will be reduced to Ag which will get deposited at the cathode. At anode : Both $\mathrm{NO}_{3}^{-}$ and $\mathrm{OH}^{-}$ ions will migrate. But $\mathrm{OH}^{-}$ ions with less discharge potential will be oxidise in preference to $\mathrm{NO}_{3}^{-}$ ions which will remain in solution. $\mathrm{OH}^{-}(a q) \rightarrow \mathrm{O}+e^{-} ; 4 \mathrm{OH} \rightarrow 2 \mathrm{H}_{2} \mathrm{O}(l)+\mathrm{O}_{2}(g)$ Thus, as a result of electrolysis, silver is deposited on the cathode while $\mathrm{O}_{2}$ is evolved at the anode. The solution will be acidic due to the presence of $H N O_{3}$ (iii) A dilute solution of $H_{2} \mathrm{SO}_{4}$ using platinum electrodes: On passing current, both acid and water will ionise as follows: $H_{2} S O_{4}(l)-\stackrel{(a q)}{\longrightarrow} 2 H^{+}(a q)+S O_{4}^{2-}(a q)$
At cathode : $A g^{+}$ ions with less discharge potential are reduced in preference to $\mathrm{H}^{+}$ ions which will remain in solution. As a result, silver will be deposited at cathode. $A g^{+}(a q)+e^{-} \rightarrow A g \quad(\text { deposited })$ At anode : An equivalent amount of silver will be oxidised to Ag" ions by releasing electrons. $A g(s)-\stackrel{(a q)}{\longrightarrow} A g^{+}(a q)+e^{-}$ Thus, the concentration of the solution will remain unaffected. (ii) An aqueous solution of $A g N O_{3}$ using platinum electrodes: In the case the platinum electrodes are the non-attackable electrodes. On passing current the following changes will occur at the electrodes. At cathode : Ag" ions will be reduced to Ag which will get deposited at the cathode. At anode : Both $\mathrm{NO}_{3}^{-}$ and $\mathrm{OH}^{-}$ ions will migrate. But $\mathrm{OH}^{-}$ ions with less discharge potential will be oxidise in preference to $\mathrm{NO}_{3}^{-}$ ions which will remain in solution. $\mathrm{OH}^{-}(a q) \rightarrow \mathrm{O}+e^{-} ; 4 \mathrm{OH} \rightarrow 2 \mathrm{H}_{2} \mathrm{O}(l)+\mathrm{O}_{2}(g)$ Thus, as a result of electrolysis, silver is deposited on the cathode while $\mathrm{O}_{2}$ is evolved at the anode. The solution will be acidic due to the presence of $H N O_{3}$ (iii) A dilute solution of $H_{2} \mathrm{SO}_{4}$ using platinum electrodes: On passing current, both acid and water will ionise as follows: $H_{2} S O_{4}(l)-\stackrel{(a q)}{\longrightarrow} 2 H^{+}(a q)+S O_{4}^{2-}(a q)$ 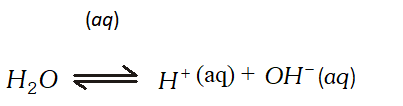 At cathode : $\mathrm{H}^{+}(\mathrm{aq})$ ions will migrate to the cathode and will be reduced to $\mathrm{H}_{2}$ H^{+}(a q)+e^{-} \longrightarrow H ; H+H \longrightarrow H_{2}(g) At anode : $O H^{-}$ ions will be released in preference to $\mathrm{SO}_{4}^{2-}$ ions because their discharge potential is less. They will be oxidised as follows: $O H^{-}(a q) \rightarrow O H+e^{-} ; 4 O H \rightarrow 2 H_{2} O(l)+O_{2}(g)$ Thus, $\mathrm{O}_{2}(g)$ will be evolved at anode. The solution will be acidic and will contain $H_{2} S O_{4} .$ (iv) An aqueous solution of $\mathrm{CuCl}_{2}$ using platinum electrodes: The electrolysis proceeds in the same manner as discussed in the case of $\mathrm{AgNO}_{3}$ solution. Both $\mathrm{CuCl}_{2}$ and $\mathrm{H}_{2} \mathrm{O}$ will ionise as follows: \begin{array}{l} {\mathrm{CuCl}_{2} \frac{(\mathrm{aq})}{2}, \mathrm{Cu}^{2+}(a q)+2 \mathrm{Cl}^{-}(a q)} \\ {\mathrm{H}_{2} \mathrm{O} \rightleftharpoons \mathrm{H}^{+}(a q)+\mathrm{OH}^{-}(a q)} \end{array} At cathode: $\mathrm{Cu}^{2+}$ ions will be reduced in preference to $\mathrm{H}^{+}$ ions and copper will be deposited at cathode $C u^{2+}(a q)+2 e^{-} \longrightarrow C u$ (deposited) At anode: $\mathrm{Cl}^{-}$ ions will be discharged in preference to $\mathrm{OH}^{-}$ ions which will remain in solution. $C l^{-} \rightarrow C l^{-}+e^{-} ; C l+C l \rightarrow C l_{2}(g)$ Thus, Cl, will be evolved at anode.
At cathode : $\mathrm{H}^{+}(\mathrm{aq})$ ions will migrate to the cathode and will be reduced to $\mathrm{H}_{2}$ H^{+}(a q)+e^{-} \longrightarrow H ; H+H \longrightarrow H_{2}(g) At anode : $O H^{-}$ ions will be released in preference to $\mathrm{SO}_{4}^{2-}$ ions because their discharge potential is less. They will be oxidised as follows: $O H^{-}(a q) \rightarrow O H+e^{-} ; 4 O H \rightarrow 2 H_{2} O(l)+O_{2}(g)$ Thus, $\mathrm{O}_{2}(g)$ will be evolved at anode. The solution will be acidic and will contain $H_{2} S O_{4} .$ (iv) An aqueous solution of $\mathrm{CuCl}_{2}$ using platinum electrodes: The electrolysis proceeds in the same manner as discussed in the case of $\mathrm{AgNO}_{3}$ solution. Both $\mathrm{CuCl}_{2}$ and $\mathrm{H}_{2} \mathrm{O}$ will ionise as follows: \begin{array}{l} {\mathrm{CuCl}_{2} \frac{(\mathrm{aq})}{2}, \mathrm{Cu}^{2+}(a q)+2 \mathrm{Cl}^{-}(a q)} \\ {\mathrm{H}_{2} \mathrm{O} \rightleftharpoons \mathrm{H}^{+}(a q)+\mathrm{OH}^{-}(a q)} \end{array} At cathode: $\mathrm{Cu}^{2+}$ ions will be reduced in preference to $\mathrm{H}^{+}$ ions and copper will be deposited at cathode $C u^{2+}(a q)+2 e^{-} \longrightarrow C u$ (deposited) At anode: $\mathrm{Cl}^{-}$ ions will be discharged in preference to $\mathrm{OH}^{-}$ ions which will remain in solution. $C l^{-} \rightarrow C l^{-}+e^{-} ; C l+C l \rightarrow C l_{2}(g)$ Thus, Cl, will be evolved at anode. 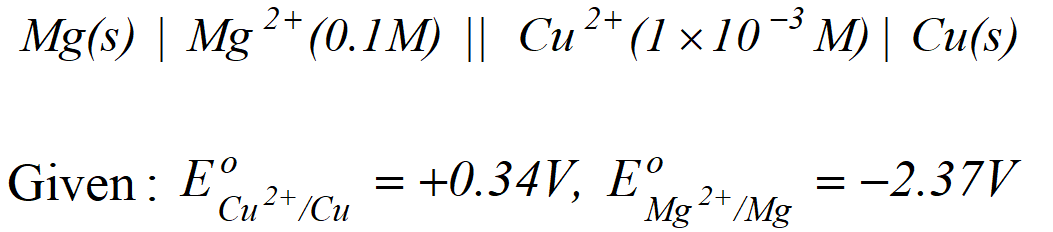 (b) Explain with example the terms weak and strong electrolytes OR (a) The resistance of a conductivity cell containing $0.001 M K C l$ solution at $298 K$ is $1500 \Omega$ what is the cell constant, it the conductivity of $0.001 \mathrm{MKCl}$ solution at $298 K$ is $0.146 \times 10^{-3} \mathrm{S} \mathrm{cm}^{-1}$ (b) Predict the product of electrolysis in the solution of H_{2} S O_{4} with platinum electrode [A.I.S.B. 2007]
(b) Explain with example the terms weak and strong electrolytes OR (a) The resistance of a conductivity cell containing $0.001 M K C l$ solution at $298 K$ is $1500 \Omega$ what is the cell constant, it the conductivity of $0.001 \mathrm{MKCl}$ solution at $298 K$ is $0.146 \times 10^{-3} \mathrm{S} \mathrm{cm}^{-1}$ (b) Predict the product of electrolysis in the solution of H_{2} S O_{4} with platinum electrode [A.I.S.B. 2007] 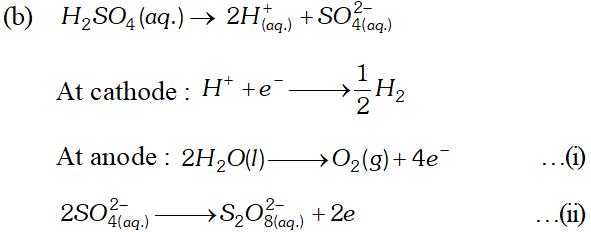 For dilute solution of $H_{2} \mathrm{SO}_{4}$ reaction (i) is preferred; in that case $\mathrm{O}_{2}$ is liberated at anode. But at higher concentration of $H_{2} S O_{4}$ reaction (ii) is preferred and peroxodisulphuric acid $\left(H_{2} S_{2} O_{8}\right)$ solution is obtained.
For dilute solution of $H_{2} \mathrm{SO}_{4}$ reaction (i) is preferred; in that case $\mathrm{O}_{2}$ is liberated at anode. But at higher concentration of $H_{2} S O_{4}$ reaction (ii) is preferred and peroxodisulphuric acid $\left(H_{2} S_{2} O_{8}\right)$ solution is obtained. 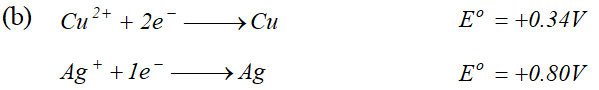 (i) Construct a galvanic cell using the above data (ii) For what concentration of $A g^{+}$ ions will the emf of the cell be zero at $25^{\circ} \mathrm{C}$. If the concentration of $C u^{2+}$ is $0.01 M ? \quad[\log 3.919=0.593]$ [A.I.S.B. 2006]
(i) Construct a galvanic cell using the above data (ii) For what concentration of $A g^{+}$ ions will the emf of the cell be zero at $25^{\circ} \mathrm{C}$. If the concentration of $C u^{2+}$ is $0.01 M ? \quad[\log 3.919=0.593]$ [A.I.S.B. 2006] 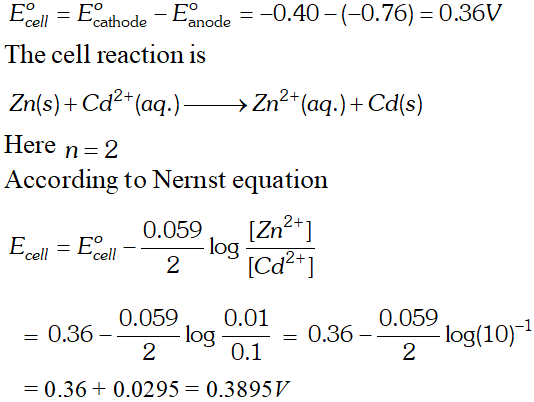 (a) (i) The alkaline medium prevents the availability of $H^{+}$ ions. This in turn reduces rate of oxidation of $F e$ to $\mathrm{Fe}^{2+} .$ Thus the rusting of iron is inhibited. (ii) Even if the zinc coating is broken in an iron pipe, the remaining zinc layer undergoes oxidation in the remaining zinc layer undergoes oxidation in preference to iron because of its more electropositive nature than iron. Hence iron does not rust. \text { (b) } \quad \text { (i) Since } E_{\mathrm{Ag}^{+} / \mathrm{Ag}}^{\circ} \text { is greater than } E_{\mathrm{Cu}^{2+} / \mathrm{Cu}}^{\circ} \mathrm{SO} reduction will occur at silver electrode. The cell representation is $C u(s)\left|C u^{2+}\right|\left|A g^{+}\right| A g(s)$
(a) (i) The alkaline medium prevents the availability of $H^{+}$ ions. This in turn reduces rate of oxidation of $F e$ to $\mathrm{Fe}^{2+} .$ Thus the rusting of iron is inhibited. (ii) Even if the zinc coating is broken in an iron pipe, the remaining zinc layer undergoes oxidation in the remaining zinc layer undergoes oxidation in preference to iron because of its more electropositive nature than iron. Hence iron does not rust. \text { (b) } \quad \text { (i) Since } E_{\mathrm{Ag}^{+} / \mathrm{Ag}}^{\circ} \text { is greater than } E_{\mathrm{Cu}^{2+} / \mathrm{Cu}}^{\circ} \mathrm{SO} reduction will occur at silver electrode. The cell representation is $C u(s)\left|C u^{2+}\right|\left|A g^{+}\right| A g(s)$ 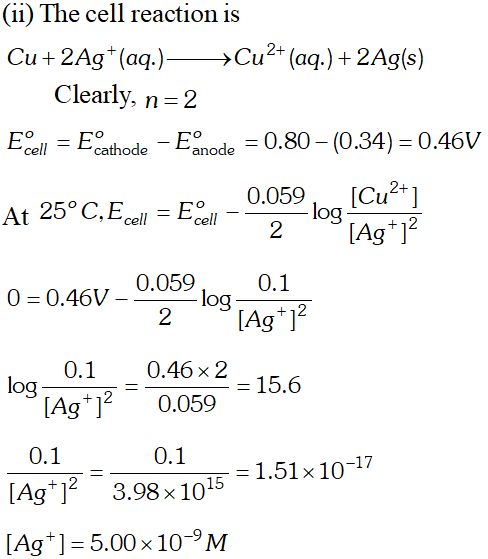
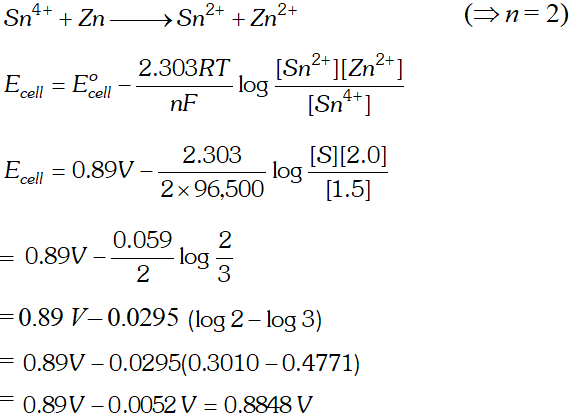
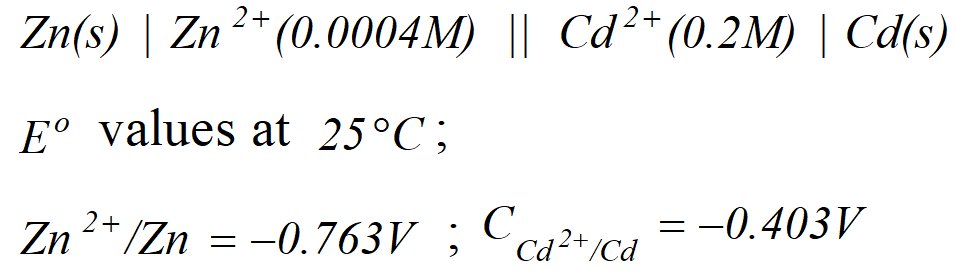
![]() [Delhi Board 2000]
[Delhi Board 2000]