Flemings Left Hand Rule Class 12 states that if we stretch the thumb, the forefinger, and the middle finger of our left hand such that they are mutually perpendicular to each other.
If the forefinger gives the direction of current and the middle finger points in the direction of the magnetic field then the thumb points towards the direction of the force or motion of the conductor.
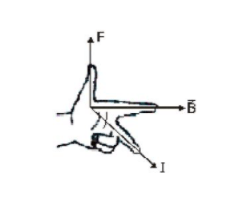Then if the forefinger points in the direction of field $(\overrightarrow{\mathrm{B}})$, the central finger in the direction of current, the thumb will point in the direction of the force.
(ii) Right-hand Palm Rule: Stretch the fingers and thumb of the right hand at right angles to each other. Then if the fingers point in the direction of field $\overrightarrow{\mathrm{B}}$ and thumb in the direction of current $\mathbf{I}$, the normal to palm will point in the direction of force.
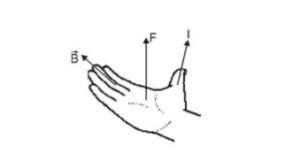Regarding the force on a current-carrying conductor in a magnetic field it is worth mentioning that :
(a) As the force BI d\ell sin \theta is not a function of position r, the magnetic force on a current element is non-central [a central force is of the form $\mathrm{F}=\mathrm{Kf}(\mathrm{r}) \overrightarrow{\mathrm{n}_{\mathrm{r}}}]$
(b) The force d\vec $\overrightarrow{\mathrm{F}}$ is always perpendicular to both $\overrightarrow{\mathrm{B}}$ and $\mathrm{Id} \vec{\ell}$ though $\overrightarrow{\mathrm{B}}$ and $\mathrm{Id} \vec{\ell}$ may or may not be perpendicular to each other.
(c) In case of current-carrying conductor in a magnetic field if the field is uniform i.e.,
$\overrightarrow{\mathrm{B}}=$ constt.,
$\overrightarrow{\mathrm{F}}=\int \mathrm{I} \mathrm{d} \vec{\ell} \times \overrightarrow{\mathrm{B}}=\mathrm{I}\left[\int \mathrm{d} \vec{\ell}\right] \times \overrightarrow{\mathrm{B}}$
and as for a conductor $\int_{\mathrm{d}} \vec{\ell}$ represents the vector sum of all the length elements from initial to final point, which in accordance with the law of vector addition is equal to the length vector $\overrightarrow{\ell^{\prime}}$ joining initial to final point, so a current-carrying conductor of any arbitrary shape in a uniform field experience a force
$\vec{F}=I\left[\int d \vec{\ell}\right] \times \vec{B}=I \ell^{\prime} \times \vec{B}$
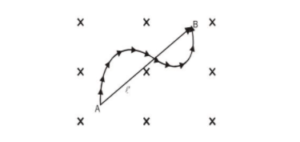where $\vec{\ell}$ is the length vector joining initial and final points of the conductor as shown in fig.
(d) If the current-carrying conductor in the form of a loop of any arbitrary shape is placed in a uniform field,
$\overrightarrow{\mathrm{F}}=\oint \mathrm{Id\vec{\ell }} \times \overrightarrow{\mathrm{B}}=\mathrm{I}[\oint \overrightarrow{\mathrm{d} \vec{\ell}}] \times \overrightarrow{\mathrm{B}}$
and as for a closed loop, $\oint \mathrm{d} \vec{\ell} \text { is always zero. [vector sum of all } \mathrm{d} \vec{\ell}]$
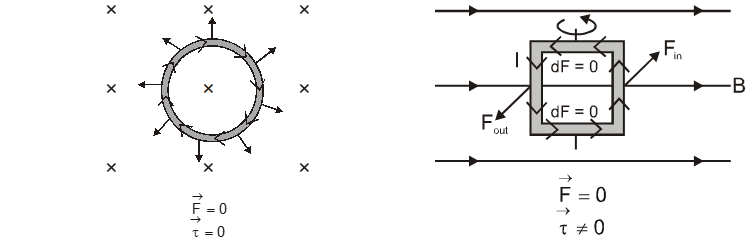
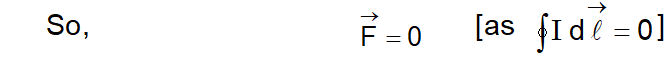i.e., the net magnetic force on a current loop in a uniform magnetic field is always zero as shown in fig.
Here it must be kept in mind that in this situation different parts of the loop may experience an elemental force due to which the loop may be under tension or may experience a torque as shown in fig.
Click here for the Video tutorials of Magnetic Effect of Current Class 12
Then if the forefinger points in the direction of field $(\overrightarrow{\mathrm{B}})$, the central finger in the direction of current, the thumb will point in the direction of the force.
(ii) Right-hand Palm Rule: Stretch the fingers and thumb of the right hand at right angles to each other. Then if the fingers point in the direction of field $\overrightarrow{\mathrm{B}}$ and thumb in the direction of current $\mathbf{I}$, the normal to palm will point in the direction of force.
Regarding the force on a current-carrying conductor in a magnetic field it is worth mentioning that :
(a) As the force BI d\ell sin \theta is not a function of position r, the magnetic force on a current element is non-central [a central force is of the form $\mathrm{F}=\mathrm{Kf}(\mathrm{r}) \overrightarrow{\mathrm{n}_{\mathrm{r}}}]$
(b) The force d\vec $\overrightarrow{\mathrm{F}}$ is always perpendicular to both $\overrightarrow{\mathrm{B}}$ and $\mathrm{Id} \vec{\ell}$ though $\overrightarrow{\mathrm{B}}$ and $\mathrm{Id} \vec{\ell}$ may or may not be perpendicular to each other.
(c) In case of current-carrying conductor in a magnetic field if the field is uniform i.e.,
$\overrightarrow{\mathrm{B}}=$ constt.,
$\overrightarrow{\mathrm{F}}=\int \mathrm{I} \mathrm{d} \vec{\ell} \times \overrightarrow{\mathrm{B}}=\mathrm{I}\left[\int \mathrm{d} \vec{\ell}\right] \times \overrightarrow{\mathrm{B}}$
and as for a conductor $\int_{\mathrm{d}} \vec{\ell}$ represents the vector sum of all the length elements from initial to final point, which in accordance with the law of vector addition is equal to the length vector $\overrightarrow{\ell^{\prime}}$ joining initial to final point, so a current-carrying conductor of any arbitrary shape in a uniform field experience a force
$\vec{F}=I\left[\int d \vec{\ell}\right] \times \vec{B}=I \ell^{\prime} \times \vec{B}$
where $\vec{\ell}$ is the length vector joining initial and final points of the conductor as shown in fig.
(d) If the current-carrying conductor in the form of a loop of any arbitrary shape is placed in a uniform field,
$\overrightarrow{\mathrm{F}}=\oint \mathrm{Id\vec{\ell }} \times \overrightarrow{\mathrm{B}}=\mathrm{I}[\oint \overrightarrow{\mathrm{d} \vec{\ell}}] \times \overrightarrow{\mathrm{B}}$
and as for a closed loop, $\oint \mathrm{d} \vec{\ell} \text { is always zero. [vector sum of all } \mathrm{d} \vec{\ell}]$
i.e., the net magnetic force on a current loop in a uniform magnetic field is always zero as shown in fig.
Here it must be kept in mind that in this situation different parts of the loop may experience an elemental force due to which the loop may be under tension or may experience a torque as shown in fig.
Current Loop in a Uniform Field
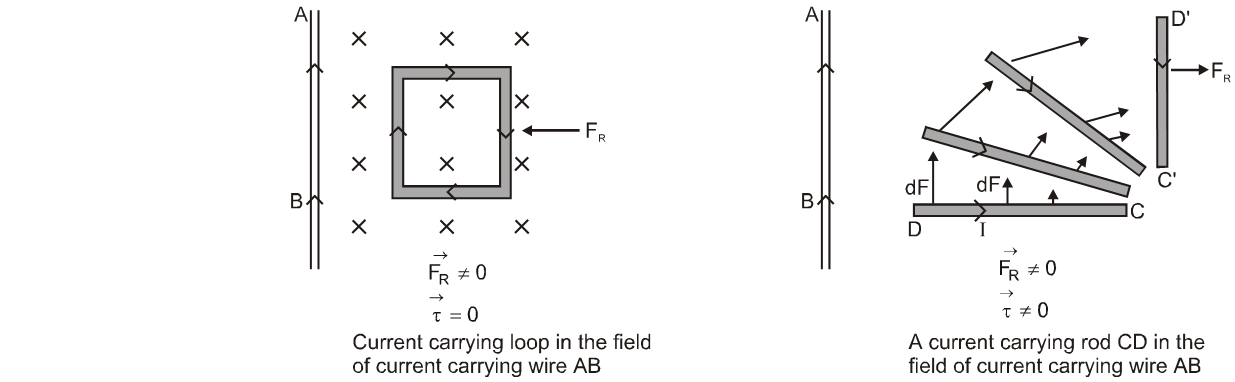
(e) if a current-carrying conductor is situated in a non-uniform field, its different elements will experience different forces; so in this situation, $\overrightarrow{\mathrm{F}_{\mathrm{R}}} \neq 0$ but $\overrightarrow{\mathrm{\tau}}$ may or may not be zero
Click here for the Video tutorials of Magnetic Effect of Current Class 12
So, that's all from this blog. I hope you get the idea about the Flemings Left Hand Rule of Class 12. If you enjoyed this article then please share it with your friends.
About eSaral At eSaral we are offering a complete platform for IIT-JEE & NEET preparation. The main mission behind eSaral is to provide education to each and every student in India by eliminating the Geographic and Economic factors, as a nation’s progress and development depends on the availability of quality education to each and every one. With the blend of education & technology, eSaral team made the learning personalized & adaptive for everyone.For free video lectures and complete study material, Download eSaral APP.